低浓度下反弹参数对固结土壤表面沙粒跃移的影响

傅林涛，蔡萌琦

(成都大学 建筑与土木工程学院，四川 成都 610106)

0 引 言

风沙运动广泛存在于地球及其他星球表面[1-3]，形成各种风蚀地貌(比如沙波纹和沙丘等)并且向大气层释放粉尘[4-5].在风的驱动下，沙粒的运动模式分为跃移、蠕移和悬移3种[6].实验数据显示,跃移占总输沙通量的比值大约为75%[4,6],且对沙丘的形成、发展[7-13]及沙波纹的变化[14-15]起到关键作用.跃移沙粒的轰击作用被证明是地球[16]和火星[17]疏松表面粉尘释放的最重要途径，而跃移沙粒长时间的冲击[18]对地球及其他行星地表雅丹地貌[19-21]的演化有重要帮助.此外，沙粒跃移也被证明是风磨石形成的关键机制之一[22-23].

起跳参数(包括速度和角度)对沙粒的跃移运动起着决定性的作用[9,24].目前已有许多关于地球[8,25]和其他星球[5]环境下起跳参数的研究，主要还是关于疏松地表的沙粒跃移，而关于固结土壤表面跃移沙粒起跳参数的研究相对较少.事实上，相比于疏松地表，由于缺少沙粒溅起过程，固结土壤表面沙粒的起跳只有沙粒反弹过程，因此在固结土壤情况下的沙粒起跳参数通常以反弹参数替代.

Rice等[26]通过风洞实验探索了跃移沙粒轰击不同强度固结土壤的过程，发现固结土壤表面跃移冲击沙粒的速度恢复系数(系数值变化范围为0.61～0.76)明显高于疏松地表上得到的速度恢复系数(系数平均值约为0.57).文献[27]通过风洞实验测量了入射角度为10°且入射速度为4.4 m/s的跃移沙粒的冲击和反弹，结果发现，随着固结土壤强度的增加，入射沙粒的恢复系数也逐渐增加.Gordon等[28]通过PTV技术测量和比较了疏松和固结土壤表面跃移沙粒的冲击和反弹响应，结果再次表明固结土壤表面的速度恢复系数(系数平均值约为0.79)高于疏松土壤表面的速度恢复系数(系数平均值约为0.64).随着入射速度的增加，由于颗粒与土壤表面的非弹性碰撞，反弹沙粒的速度恢复系数逐渐降低.虽然入射颗粒与土壤表面碰撞后的平均反弹角度大约是入射角度的2倍，但由于沙粒的非规则性及表面粗糙度，反弹角度一般分布在0°～90°.O’Brien等[29]也在风洞实验中测量过沙粒在固结土壤表面跃移的情况，但未能明确区分反弹沙粒与溅起的小颗粒，无法进一步做定量分析.

事实上，在稀疏植被覆盖的干旱和半干旱地区，沙粒在固结土壤表面跃移的现象非常常见[30-31].此外，遥感影像数据分析表明，火星沙丘场的沙源来自距离较远的其他地方[32]，且沙粒由沙源地传输到沙丘场时会经过固结土壤地表.因此，本研究拟通过数值计算来定量评估低输沙强度下反弹参数对固结土壤表面沙粒跃移的影响，且为了使得结果具有一般性，主要探讨地球、火星和金星3种环境下反弹参数对跃移沙粒的速度恢复系数、入射速度、入射角度和跃移长度的影响.

1 研究方法

1.1 风速廓线

(1)

通过与流场交换能量，跃移沙粒可以减小风速而改变风速廓线[4,7-8].由于本研究主要考察低沙粒浓度情况下的跃移，因此计算中忽略了跃移沙粒与流场的相互作用.这里，平均垂向速度设为0,平坦地表上平均水平速度的垂向廓线[6]由式(1)给出.其中，u*是摩擦速度，κ是冯卡门常数，z是垂向坐标，z0是表面动力粗糙度.基于文献[33]，z0由式(2)给出，其中，Rek=ρaksu*/μ为颗粒雷诺数，ρa和μ分别是空气密度和运动粘度，ks为特征粗糙长度(取值为D[34]).

1.2 颗粒运动

(3)

(4)

(5)

大气边界层中沙粒跃移受到多种外力作用[9],但通常主要考虑重力和拖曳力[35].此外，这里只考虑沙粒平动而不考虑转动[36]，因而沙粒跃移可以由式(3)计算.其中，xp和zp分别是沙粒的水平和垂向坐标，m是沙粒质量，g是重力加速度，ρs是沙粒密度，CD=[(32/ReD)2/3+1]3/2是天然沙粒的拖曳力系数[37],且ReD=ρaD|Vr|/μ，而Vr是沙粒与周围流体的相对速度.计算过程中，跃移沙粒的起跳初值条件由式(4)给定，其中Vx和Vz分别是颗粒的水平和垂向速度分量.经过粒床碰撞后，跃移沙粒的反弹速度由式(5)给定，V0和θ0分别为沙粒的反弹速度和角度.

1.3 反弹参数的确定

(6)

虽然已有一些关于颗粒-颗粒碰撞[38-39]和颗粒-壁面碰撞[40]的理论研究，但自然沙粒的不规则性和床面分布的多样性会导致实际碰撞过程变得复杂，从而阻碍这些理论研究的实际应用.实际应用中[8-9,36]，一些经验值或经验表征更具有实用价值.测量结果表明，反弹参数依赖于跃移沙粒的入射速度[23,28,41-42]和入射角度[41-42]，且分布在相对较宽的范围[28-29].由于数据分析显示切向脉冲在碰撞过程中的贡献相对较小[28],因此，根据文献[28,43-44]，入射速度的恢复系数e(反弹速度V0与入射速度Vi的比值)和反弹角度的经验表征可以由式(6)确定.由文献[43]可知，A1a=-1.153 44,A1b=0.898 26,A1c=-0.483 58，A1d=0.285 28.这样，从式(6)可以看出，反弹参数的确定最终由B1k、A2k和B2k3个参量共同影响.表1给出了本研究中不同参量组合类型的具体取值情况.

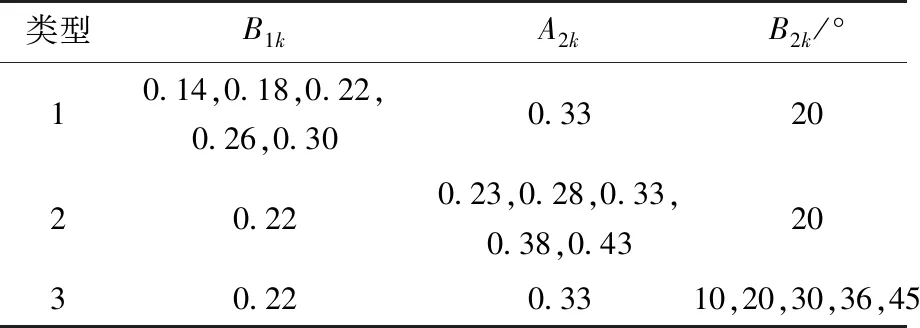
表1 反弹参数中的B1k、A2k和B2k

其中，数值A2k=0.33、B1k=0.22及B2k=20°均来自实际实验数据[28,44].

1.4 相关参数及其他设置

为了方便比较，3个星球(地球、火星和金星)环境下的平均粒径D都取值为0.25 mm[5],且D在3个星球表面对应的疏松土壤流体启动临界值[45]依次分别为0.27、1.56、0.038 m/s.地球和火星上的冲击临界速度值分别为0.20和0.23 m/s[5],因为金星上的冲击临界速度(约0.146 m/s[5])远高于流体临界，所以通常不考虑[3]在冲击临界风速情况下的沙粒跃移.计算过程中涉及的大气和其他物理参数列举在表2中[5,34].当所有关注物理量的相对变化小于0.001时，即判断为计算收敛.在计算过程中，沙粒的垂向起跳速度小于(gD)1/2时，则认为沙粒在床面蠕移或停止在床面，不再作为跃移沙粒.

表2 计算过程中涉及的大气和物理参数

2 研究结果

计算收敛后，最终稳定的4个物理量,即速度恢复系数(e)、入射速度(Vi)、入射角度(θi)和跃移长度(L),被记录下来用作分析.如果沙粒的垂向起跳速度小于(gD)1/2时，此4个物理量的值标记为NA.

2.1 地球环境下B1k对跃移相关物理量的影响

由式(6)可知，参量B1k的改变实际反映的是恢复系数设置的改变.图1给出了地球环境下跃移相关的4个物理量(e、Vi、θi和L)随B1k(即恢复系数设置)的定量变化.从图1可知，所有物理量随着参量B1k的增加而逐渐降低.基于最小二乘法的进一步定量分析表明，这些物理量都随B1k线性减小.在相同入射速度下，B1k越大，则恢复系数越小.如果沙粒的启动初值和来流风速相同，入射速度将随B1k减小.而当固定反弹角度后，反弹速度及其水平和垂向速度分量也都随B1k减小，即解释了跃移长度随B1k减小的情况(跃移长度主要受反弹速度的水平分量影响).由图1可得，流体临界风速下的入射速度和跃移长度大约是冲击临界风速下的2倍，因而根据式(6)可知,恢复系数随着风速降低.由于入射角度定义为入射速度的垂向和水平分量的比值[46]，所以在相同风速下入射角度随B1k减小意味着跃移沙粒的垂向速度分量比水平速度分量对B1k更敏感，在相同B1k下入射角度随风速减小意味着跃移沙粒的水平分量比垂向速度分量对风速更敏感.

2.2 地球环境下A2k和B2k对跃移相关物理量的影响

由式(6)可知,参量A2k和B2k的改变实际反映的是反弹角度设置的改变.图2和图3给出了地球环境下跃移相关的4个物理量(e、Vi、θi和L)随A2k、B2k(即反弹角度设置)的定量变化.

从图2和图3可知，4个物理量对A2k和B2k的响应与对B1k的响应存在差异.跃移稳定后的恢复系数虽然存在轻微的变化，但几乎不会随A2k降低，却会随着B2k的增加而呈指数形式降低.此外，在相同风速下，跃移长度、入射速度和入射角度都随着A2k和B2k增加.定量分析表明，在选定的参量取值范围内，此3个物理量随着A2k线性变化，但随着B2k指数变化.

2.3 星球环境的影响

为了更好地理解环境改变的影响，定义不同环境下4个物理量的最大相对变化值为(Cmax-Cmin)/Cmin，其中Cmax(或Cmin)代表着在选定的参量取值范围内某个物理量的最大值(或最小值).如果Cmin等于0(指由于反弹速度的垂向分量小于(gD)1/2而使得跃移不再维持或继续)，最大相对变化值将标记为Nan.表3和表4分别表示在冲击临界风速和流体临界风速情况下的分析结果.

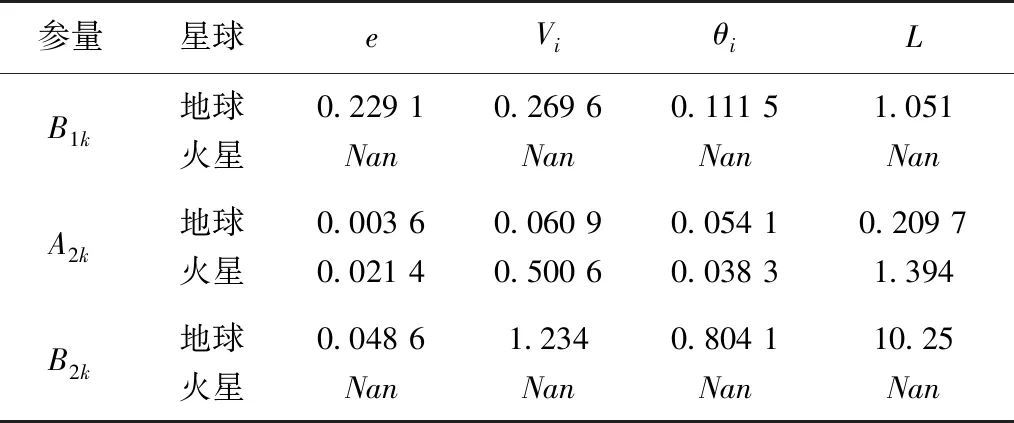
表3 冲击临界风速下地球和火星环境中最大相对变化值的比较

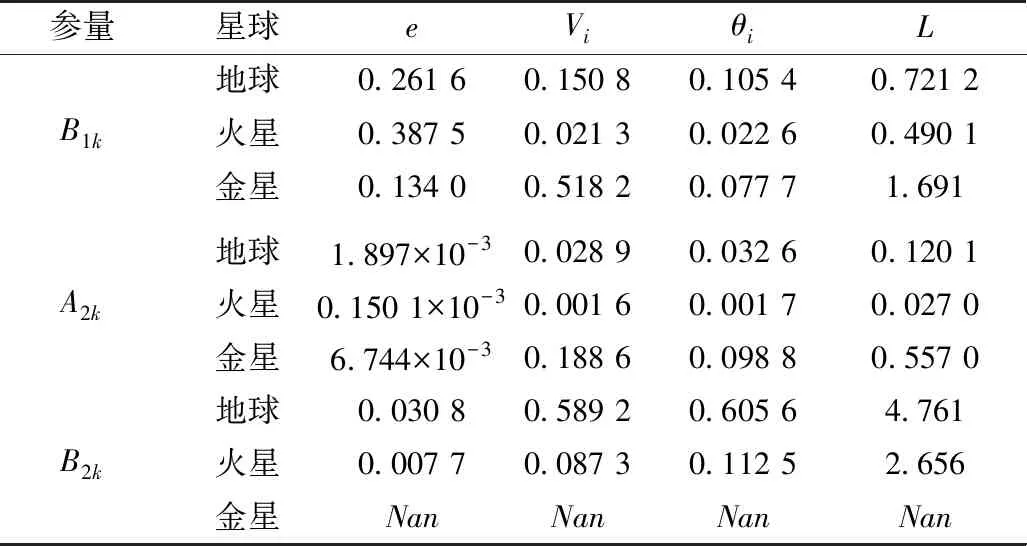
表4 流体临界风速下地球、火星和金星环境中最大相对变化值的比较

表3显明，在冲击临界风速下火星环境对沙粒跃移有非常重要的作用.在选定的参量取值范围内，地球环境下的沙粒跃移均可以维持，然而火星环境下的沙粒跃移仅可以在大B1k和小B2k取值情况下维持.总之，相比于其他2个参量，A2k对跃移相关的4个物理量的影响最低.在地球上，除了由参量B1k主导的恢复系数，入射速度、入射角度和跃移长度对参量B2k更加敏感.虽然由B2k引起的恢复系数最大变化低于5%，但由B2k为最大值时计算得到的跃移长度10倍多于B2k为最低值时的跃移长度.

表4显示风速的增加并不定性地改变跃移相关的4个物理量对3个参量的响应,意味着，相比于B1k和B2k，3个星球环境下A2k都保持着其最弱的影响.4个物理量中，跃移长度对所有3个参量的敏感性最高.流体临界风速下，B1k对4个物理量的影响依赖环境.由B1k引起的恢复系数、入射速度、入射角度和跃移长度的最大相对变化分别发生在地球、火星和金星环境下.A2k和B2k在金星环境下的影响比在地球和火星环境下更显著.风速的增加会降低4个物理量对3个参量变化的相对响应.此外，随着风速的增加，3个星球环境下A2k对恢复系数的影响逐渐可以忽略.

3 讨 论

沙粒在颗粒形成的床面上跃移是非常复杂的过程.由于关于沙粒在固结土壤表面的研究较少，本研究中3个参量取值的一部分来自于疏松床面的实验结果.考虑到一些可能的变化，A2k和B1k均由地球环境下的实验结果获得.根据已有关于外地行星上的风沙运动[11,36]，参量B2k取了较宽的范围.因此，本研究获得的结果不仅对了解固结土壤表面沙粒输运有帮助，同样也对沙源有限情况下(尤其是在冲击临界风速附近)风沙运动的数值模拟有潜在帮助.虽然基于表2列举的参量值计算得到沙粒跃移的相关物理量可能与实际情况存在定量上的差异，但物理量的定性变化规律是有实际意义的.

从物理意义的角度看，式(6)中参量B1k体现的是床面的力学强度.自然环境的多样性和实验处理过程的不同[26-28]均可以导致床面强度的改变.图1也表明恢复系数设置对沙粒跃移的影响是综合性的.所有这些结果为相近风速下野外和室内实验测量(尤其是重度退化草地的结皮地表[31]和沙漠与绿洲之间的过渡带[47])的风沙运动存在的差异提供了一个可能的解释.

参量A2k和B2k体现了粒床碰撞过程中切向阻力的相对作用[40].由于B2k引起的反弹角度变化更大，沙粒跃移对B2k比对A2k更敏感.当然，计算结果也显示沙粒跃移对反弹角度比对恢复系数更敏感.然而，由于法向和切向恢复系数的非线性关系[38,40]，当入射速度和入射角度固定时，准确给出入射沙粒的反弹角度通常是困难的.因此，除了使用恢复系数(e)和它的垂向分量(ez)作为约束条件来经验性地求得反弹角度[48]外，36o[34,36,49]和45o[8]是风沙运动模拟中常用的反弹角度.虽然在地球环境下冲击临界风速时由这2个反弹角度造成风沙运动相关量的相对变化可以达到约20%，但是这个相对变化可能由于星球环境的改变而增大.

本研究结果表明，星球环境的改变可以对沙粒运动产生不同的影响.虽然火星的低重力可以使得其表面的沙粒比地球表面的沙粒更容易离开床面[24]，火星的稀薄空气却会导致较大的地表动力粗糙度(z0)(参考式(2))，此就进一步要求沙粒需要有更大的垂向起跳速度(垂向反弹速度)，也解释了在冲击临界风速附近时火星上的沙粒运动比地球上的沙粒运动对A2k和B2k更敏感.在金星上，较高的空气密度提高了其在水平和垂向的沙粒运动的作用.因此，拖曳力在沙粒垂向运动上的负反馈使得金星上跃移相关的4个物理量对反弹角度有比地球和火星上更高的敏感性.

风速的增加会减弱反弹参数对沙粒跃移的影响.由于在低沙粒浓度时风速与入射速度正相关，本研究采用的低风速意味着低的入射速度.因此，针对低速跃移沙粒的反弹参数的选择应当慎重.数值模拟[49-50]和实验测量[46,51]也表明在充分发展的风沙流中存在大比例的低速跃移沙粒.不同的反弹参数选择可能导致预测的跃移特征物理量(特别是在外地行星环境下[8,34,36-37])产生较大差异.