单轴旋转惯导纬度误差和航向误差关联性分析
王 超,郭正东,高大远,朱海荣
(海军潜艇学院,山东青岛266199)
惯导航向信息是舰船导弹发射的重要基准信息,惯导航向精度直接决定了舰船导弹武器系统的作战效能。目前,单轴旋转激光陀螺惯导系统已广泛应用于国外水面作战舰船,以保障舰船自主导航和为舰船武器系统发射提供信息基准[1-4]。此外,惯导姿态精度也直接影响航天测量船测控设备的外测精度[5]。在海上动态条件下,受海况、舰船运动等因素的影响,舰船姿态不断变化。海上长时间工作的舰船惯导系统,受各种误差因素的影响,其航向精度不断变化,一般可通过天文导航或GPS姿态测量方式,获取高精度航向参考信息,实现对舰船惯导航向误差进行测量和补偿[6-8]。而对于长时间海上航行的舰船而言,当受到气候或其他因素影响,无法适时进行星体测量时,即便能够获取准确的位置参考信息,也无法对舰船惯导航向误差进行实时动态评估。
考虑单轴旋转惯导纬度误差和航向误差都是在相同误差源的作用下,由惯性导航解算输出的结果,通过研究引起单轴旋转惯导航向误差和纬度误差的机理,并进行比较分析,确定二者之间的关联性,在无外界参考航向信息情况下,为实现海上舰船单轴旋转激光陀螺惯导航向误差实时动态评估与补偿,提供一种新的思路和方法。
1 引起单轴旋转惯导纬度误差机理分析
单轴旋转惯导系统误差因素主要包括初始误差、陀螺漂移、加速度计偏差、安装误差、标度因数误差和随机误差等。
单轴旋转可以自动补偿与转轴垂直方向的加速度计零位偏差、陀螺常值漂移、安装误差和对称性标度因数误差等。等效方位陀螺常值漂移和初始姿态误差是影响单轴旋转惯导系统导航误差最主要的因素[9-13]。
根据旋转惯导系统误差方程[14],主要考虑等效方位陀螺常值漂移和初始姿态误差的影响,解算出静基条件下的单轴旋转惯导纬度误差的表达式为:

式(1)中,a1、a2、a3、a4分别为误差系数,各误差系数表达式为:

式(2)中:δφ(t)为惯导纬度误差;εU为惯导等效方位陀螺常值漂移;φE0、φN0、φU0分别为惯导姿态角初始误差;φ 为舰船纬度;ωie为地球自转角频率;ωs为舒拉周期振荡角频率。
根据式(1)和式(2),纬度误差在等效方位陀螺漂移的作用下,引起纬度舒拉周期振荡误差、地球周期振荡误差和误差分量kεU等。
在动基座条件下,舰船纬度不断变化,在一段时间内,当纬度变化不大时,误差分量kεU可近似为纬度常值误差分量,可通过计算该时间段内的纬度误差均值获得。如当纬度为36°时,等效方位陀螺常值漂移为0.001(°)/h 时,引起的误差分量kεU约为0.184 9′,当纬度为76°时,引起的误差分量kεU约为0.055 3′;在初始姿态误差的影响下,主要引起纬度舒拉周期振荡误差和地球周期振荡误差。通过将惯导系统工作在水平阻尼状态[15-16],可消除惯导误差中受傅科周期调制的舒拉周期振荡误差分量,在水平阻尼工作状态,式(1)中的系数表达式为:


利用式(4)对式(3)进一步化简,得:

根据式(5),在水平阻尼工作状态下,当载体纬度变化较小时,在等效方位陀螺漂移的作用下,引起单轴旋转惯导纬度地球周期振荡误差和近似纬度常值误差分量;在初始姿态误差等误差源的作用下,主要引起纬度地球周期振荡误差。
2 引起单轴旋转惯导航向误差机理分析
根据单轴旋转惯导系统误差方程,主要考虑等效方位陀螺常值漂移和初始姿态误差的影响,解算出静基条件下的单轴旋转惯导航向误差的表达式为:

式(6)中,b1、b2、b3、b4分别为上式中的误差系数。
由于在水平阻尼工作状态下,受傅科周期振荡调制的舒拉周期振荡误差分量受到抑制,惯导航向误差主要呈现地球周期振荡特点,则在水平阻尼工作状态下,式(6)中的系数表达式为:

利用式(4)对式(7)进一步化简,得:

根据式(8),各误差源对应系数均呈现地球周期振荡,即在等效方位陀螺常值漂移和初始姿态误差等误差源的作用下,惯导航向误差呈现地球周期振荡特点。
3 单轴旋转惯导纬度误差和航向误差关联性分析
对比式(5)和式(8),则由等效方位陀螺漂移引起的纬度误差和航向误差系数表达式为:

由初始姿态误差引起的纬度误差和航向误差系数表达式为:

根据式(9)(10)可知,当补偿纬度误差分量kεU后,在水平阻尼状态下,等效方位陀螺常值漂移和各初始姿态误差分别引起惯导纬度和惯导航向地球周期振荡误差。引起的地球周期振荡误差的幅值和相位关系如表1所示。
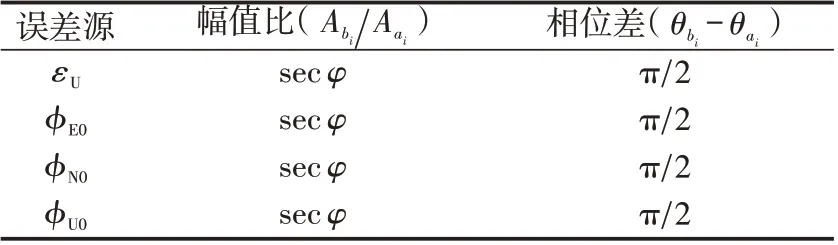
表1 单轴旋转惯导纬度误差和航向误差比较Tab.1 Comparison of latitude error and heading error of SRSINS
表1中:AbiAai为式(9)和式(10)中不同误差源对应单轴旋转惯导纬度误差和航向误差系数地球周期振荡幅值比,i=1,2,3;θbi-θai为式(9)和式(10)中不同误差源对应纬度误差和航向误差系数地球周期振荡相位差,i=1,2,3。根据表1可知,在等效方位陀螺常值漂移和初始姿态误差等误差源的作用下,单轴旋转惯导航向误差地球周期振荡幅值为纬度误差地球周期振荡幅值的sec φ 倍,航向误差地球周期振荡相位比纬度误差地球周期振荡相位提前π2。因此,在等效方位陀螺常值漂移和各初始姿态误差作用下,当补偿纬度误差分量kεU后,水平阻尼状态下单轴旋转惯导纬度误差和航向误差关联性模型如下:

式(11)中:Aδφ为纬度误差中地球周期振荡误差分量的幅值;AφU为航向误差中地球周期振荡误差分量的幅值;θδφ为纬度误差中地球周期振荡误差分量的相位;θφU为航向误差中地球周期振荡误差分量的相位。
根据式(11),航向误差中地球周期振荡误差分量的幅值是纬度误差中地球周期振荡误差分量幅值的sec φ 倍,纬度误差中地球周期振荡误差分量的相位与航向误差中地球周期振荡误差分量的相位相比,延迟π2。
以上主要考虑等效方位陀螺常值漂移和初始姿态角误差等主要误差源的影响。实际上,影响惯导航向误差和纬度误差的误差源还包括随机误差、安装误差、标度因数误差等。由于这些误差源影响相对较小,式(11)同样适用于单轴旋转惯导多种误差源共同作用下纬度误差和航向误差之间的关联性。在水平阻尼工作状态下,确定单轴旋转惯导纬度误差和航向误差存在如下关联性:①纬度误差主要包括地球周期振荡误差和误差分量kεU,航向误差主要为地球周期振荡误差;②航向误差地球周期振荡幅值为纬度误差地球周期振荡幅值的sec φ 倍;③航向误差地球周期振荡相位比纬度误差地球周期振荡相位提前π2。通过以上分析,利用水平阻尼状态下的单轴旋转惯导纬度误差和航向误差的关联性,为实现惯导航向误差实时动态评估提供一种新的思路和方法。
4 仿真实验验证
1)仿真实验设计。为验证利用纬度误差与航向误差关联性,在仿真实验设计中,结合当前文献中高精度旋转激光惯导中激光陀螺和加速度计的主要技术参数以及安装误差、标度因数误差、初始误差等误差参数[17-18],设置仿真实验条件。根据单轴旋转激光陀螺惯导运动学方程,建立水平阻尼单轴旋转激光惯导仿真模型,将惯性导航解算输出的导航参数与参考基准进行比较,获得水平阻尼工作状态下的单轴旋转激光陀螺惯导纬度误差和航向误差仿真数据,单轴旋转惯导误差仿真过程见图1。以仿真输出的纬度误差和航向误差数据为对象,利用仿真输出的纬度误差,通过计算和补偿纬度误差常值分量,根据式(11)对航向误差进行实时动态估计,比较实时动态估计的航向误差与仿真输出的实际航向误差之间的变化特点,验证单轴旋转惯导纬度误差与航向误差关联性分析的正确性。

图1 单轴旋转惯导误差仿真示意图Fig.1 Simulation diagram of error of SRSINS
结合文献中激光惯导中激光陀螺和加速度计的主要技术参数以及安装误差、标度因数误差、初始误差、单轴旋转方案等参数[1,12],设置仿真条件如下:3个激光陀螺的常值漂移均为0.001(°)/h,随机漂移标准差均为0.000 5(°)/h;3 个加速度计的零偏均为0.01 mg,随机白噪声标准差为0.005 mg;陀螺和加速度计的对称性标度因数误差均为2 ppm ;安装误差阵为[0,4″,-4″;-4″,0,4″;4″,-4″,0] ;初 始 姿 态 误 差 为[1 .0′,1.0′,2.0′] ;初始航向为90°,初始经度、纬度分别为122 °E 和76° N,惯导一直工作在水平阻尼状态,仿真时间为30 d。
2)仿真结果与分析。在水平阻尼状态下,单轴旋转惯导纬度误差和航向误差如图2所示。

图2 纬度误差与航向误差仿真曲线Fig.2 Simulation curve of latitude error and heading error
实线表示单轴旋转惯导仿真输出的纬度误差;虚线表示单轴旋转惯导仿真输出的航向误差。由图2可知,在水平阻尼工作状态下,惯导纬度误差和航向误差均主要呈现地球周期振荡性特点,且地球周期振荡幅值随时间发生变化。如在0~10 d时间段内,纬度误差 变 化 范 围 为( - 1.6′,1.8′) ;航 向 误 差 变 化 范 围 为( - 6.7′,7.1′) ,在11~20 d 时间段内,纬度误差变化范围为(- 1.7′,1.8′) ,航向误差变化范围为( - 7.5′,7.2′) ;在21~30 d 时间段内,纬度误差变化范围为(- 1.6′,1.7′) ,航向误差变化范围为( - 7.3′,7.0′) 。在不同时间段内,惯导纬度误差和航向误差的标准差和误差均值如表2所示。
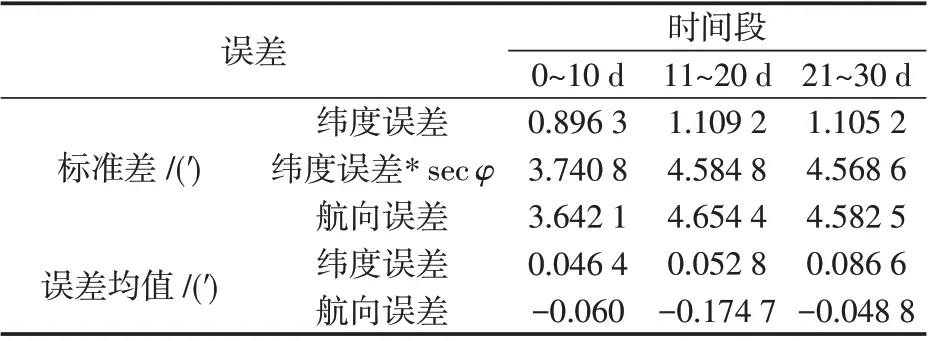
表2 不同时间段内的纬度误差和航向误差Tab.2 Latitude error and heading errorin different periods
由表2可知,在不同时间段内,单轴旋转惯导航向误差标准差与纬度误差*sec φ 基本保持一致,惯导航向误差的标准差值约为纬度误差标准差值的sec φ倍;纬度误差均值主要与等效方位陀螺常值漂移引起的误差分量有关。结合仿真条件参数,在相应时间段内,舰船纬度为76 °N,表2 中纬度误差均值与误差分量kεU计算值相近,与前面单轴旋转惯导纬度误差和航向误差关联性分析结果一致。
为进一步验证单轴旋转惯导纬度误差和航向误差地球周期振荡相位之间的关系,根据单轴旋转惯导纬度误差和航向误差关联性模型,在补偿纬度误差均值的基础上,对纬度误差地球周期振荡幅值和相位进行相应调整,可获得惯导航向误差实时动态估计值。取图2 中10~25 d 时间段内的纬度误差和航向误差数据,在计算并补偿纬度误差常值分量的基础上,根据式(11),利用惯导纬度误差对惯导航向误差进行动态估计,如图3所示。
图3 中,点虚线为利用惯导纬度误差估计出的航向误差曲线,实线为单轴旋转惯导仿真输出的实际航向误差曲线。从图中可以看出,估计的航向误差曲线与实际航向误差曲线在振荡周期、振幅和相位等方面都较好地保持了一致性,从而验证了单轴旋转惯导纬度误差和航向误差之间关联性分析的正确性。同时,验证了利用惯导纬度误差实现对航向误差进行实时动态估计可行性。利用估计的惯导航向误差对惯导实际航向误差进行补偿,如图4所示。

图3 单轴旋转惯导航向误差曲线Fig.3 Curve of heading error of SRSINS
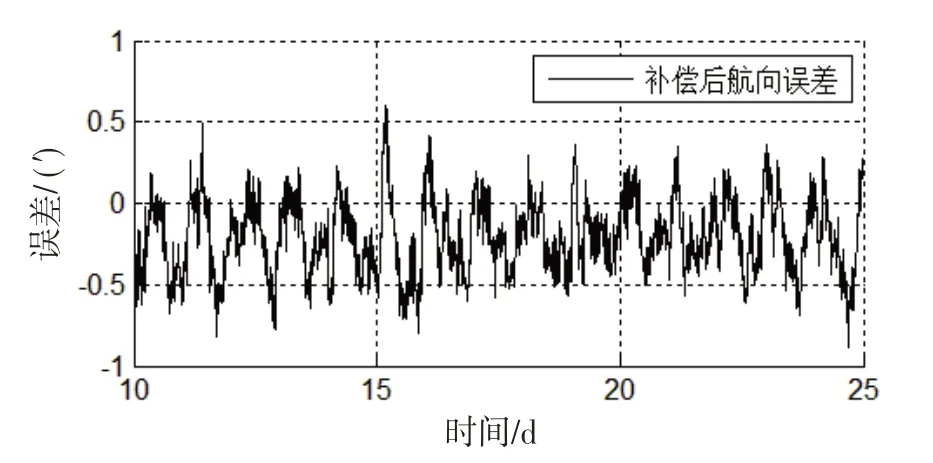
图4 补偿后航向误差曲线Fig.4 Curve of heading error after compensation
根据图4,利用估计的惯导航向误差对惯导航向误差补偿后,惯导航向误差明显降低,振荡范围约为( - 0.89′,0.61′) ,标准差约为0.23′,与补偿前单轴旋转惯导实际航向误差相比,航向误差振荡范围减小了89.8%,航向误差标准差减小1个数量级以上,大大提升了单轴旋转惯导航向精度。
5 结论
为分析在相同误差源作用下的单轴旋转惯导纬度误差和航向误差间的关联性,通过研究引起单轴旋转惯导航向误差和纬度误差的机理,并进行比较分析,建立了单轴旋转惯导纬度误差与航向误差间的关联性模型,为实现无外界参考航向信息情况下的舰船单轴旋转惯导航向误差动态评估与补偿,提供了一种新思路,对提高舰船惯导航向精度,保障舰船航行安全和提升舰船武器系统作战效能具有重要实用价值。

