导弹复合控制系统的模糊逻辑控制分配

陈 洁，赵红超，王 磊，王书湖

（1.海军航空大学，山东烟台264001；2.烟台南山学院，山东龙口265713）

直接力/气动力复合控制（以下简称直气复合控制）技术在国际上已经成为高精度、快速响应制导控制领域中必须直面的研究内容。在强烈的军事需求和广泛的应用背景下，直气复合控制技术飞速发展。直气复合控制是指通过反作用射流装置所产生的直接力和舵面所产生的气动力的共同作用，产生复合控制力矩对导弹进行控制，实现大幅度提高导弹快速响应能力和机动能力的控制方式。对于直气复合控制的研究主要集中在2 个方面：一方面对复合控制指令的控制分配与侧喷发动机开关机策略的研究，受到复合控制方式、配置方式的影响，开关机策略以及指令产生方式也不同；另一方面对复合控制条件下控制算法设计的研究，通过设计合理的控制算法发挥复合控制的优势，在保证系统的稳定性以及鲁棒性的同时，提高系统的响应性能[1]。

在高空拦截机动目标时，由于动压低、气动尾舵响应慢，非最小相位特性明显，这严重地影响空空导弹的制导控制精度。必须集中2 套执行机构的优点，消除缺点，设计出响应速度快、极限过载大和机动能力强的复合控制系统[2]。控制分配问题是设计复合控制系统时必须解决的一个关键问题。控制分配是将复合控制指令以一定的规则分配到各执行机构或控制装置上，以确保导弹的稳定性和机动性。文献[3]针对直接力和尾舵复合控制导弹设计了俯仰平面模糊逻辑自动驾驶仪，模糊逻辑控制器输出为直接力控制信号和舵偏角控制信号，但文中没有研究控制分配问题；文献[4]采用直接力控制对气动力控制进行误差补偿，设计了一种基于误差修正的直气复合控制双层姿态控制方法；文献[5]针对空空导弹的复合控制问题，设计了一种非奇异快速终端滑模控制和动态控制分配技术相结合的复合控制策略；文献[6]研究了一种直接侧向力与气动力复合控制的敏捷型导弹自动驾驶仪设计方法，对虚拟控制量采用动态控制分配算法分配给2个执行机构；文献[7]研究的导弹直接力/气动力复合控制系统中，气动力设计为滑模控制的等效控制项，直接力则设计为切换控制项；文献[8]在空空导弹越肩发射敏捷转弯的复合执行机构中，也是将气动舵作为等效控制，直接力作为切换控制，设计了滑模控制律；文献[9]将气动力和直接力进行组合，构造复合控制量，采用终端滑模控制方法设计了控制律；文献[10]采用自适应滑模变结构控制方法设计了气动力控制，对直接力控制采用模糊控制方法控制脉冲发动机的开启；文献[11]针对姿控式复合控制导弹进行了制导与控制一体化设计，采用加权伪逆法完成2 种执行机构的控制分配；文献[12]在拦截弹直气复合控制系统中，将直接力转换为等效舵偏角，与气动力合并进行控制，没有研究控制分配问题；文献[13]研究了复合控制的高速动能导弹，采用气动力和脉冲推力共同控制导弹的飞行，没有研究控制分配问题；文献[14]研究了拦截弹直气复合控制系统，采用基于LMI的权值优化伪逆法完成2种执行机构的控制分配。文献[15]针对拦截弹直气复合控制问题，建立了带约束二次规划模型，利用有效集法实现2种执行机构的控制分配。

尽管有人对空空导弹的直气复合控制系统进行了一定的研究，但是对于复合控制指令的控制分配问题的研究还不够深入。为此，本文提出了一种模糊逻辑控制分配算法。为了提高空空导弹的制导控制精度，在末制导阶段控制作用以直接力为主，气动力为辅。利用模糊逻辑控制分配算法解算出直接力控制子系统在复合控制系统中所占的权重为Wrcs（0 ≤Wrcs≤1），而气动力控制子系统所占的权重为1-Wrcs，有效地解决了控制分配问题。

1 导弹的复合控制系统

借鉴文献[5]所述的复合控制导弹的弹体配置方式以及弹体姿态运动的数学模型，以导弹纵向运动为例进行研究。在文献[5]的数学模型基础上，考虑到导弹复合控制系统的建模误差、外界干扰和侧向喷流干扰等因素的影响，导弹纵向运动的数学模型描述为：

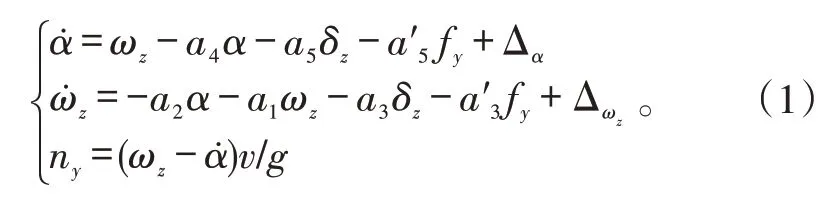
式（1）中：δz为舵偏角控制信号；fy为直接力控制信号；Δα、Δωz分别为包含了建模误差、外界干扰和侧向喷流干扰的总扰动项；其他各项变量的物理意义参见文献[5]。

复合控制系统采用过载控制方式，可测量的状态量包括ny和ωz，α 不可测。因此，须进行状态变换，将式（1）转换为以ny和ωz表征的状态方程形式：

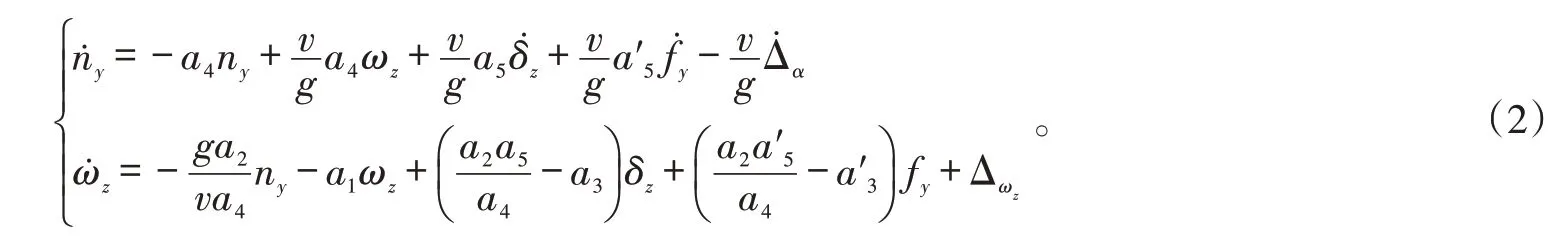
将式（2）的第1个方程右端后3项进行汇总，记为ΔΣ1，称之为“汇总不确定项”，即

定义状态量为：

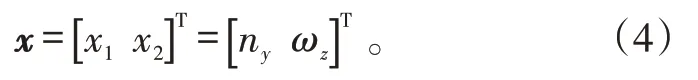
定义复合控制量为：

从而得到复合控制系统的数学模型如下：

2 复合控制量设计

复合控制系统（6）中，u 是被控输入量。下面采用动态面控制方法[16]设计控制律，系统（6）是一个二阶系统。因此，控制律的递推过程包括以下2个步骤。

步骤1：针对系统（6）的第1 个子系统，即ny子系统，定义第1个误差面为，

式中，x1c为过载指令信号。

对于汇总不确定项ΔΣ1，采用扩张状态观测器[17]对其进行估计。将ΔΣ1看作是未知的被扩张的状态变量：ξ1=ΔΣ1，并设ξ̇1=ζ(t)，ζ(t)是未知函数。由此，将ny子系统变换为：

相应地，第1个扩张状态观测器ESO1设计为：

式（9）中：d01＞0 ，d02＞0 ，0 ＜λ1＜1，0 ＜h1＜1；fal( ∙)函数的表达式为：

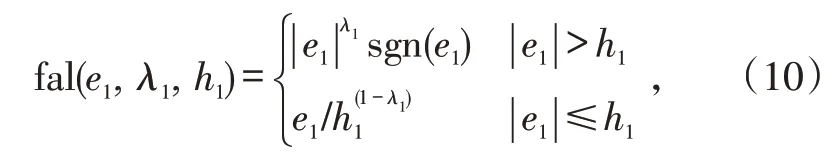
式中，sgn( ∙)是符号函数。

ESO1的状态量z2能够很好地估计ΔΣ1。因此，在控制律设计中，将以z2代替式（6）中的ΔΣ1。对式（7）求导，整理可得，

采用动态面控制方法，将x2作为ny子系统的虚拟控制量，选取其期望值为：

式中，k1＞0。

选取Lyapunov函数如下：

对式（13）求导，并设x2→，整理可得：

显然，当t →∞时，Vs1→0，即s1→0，表明x1→x1c。

步骤2：针对系统（6）的第2 个子系统，即ωz子系统，定义第2个误差面为，

式中，x2c为角速度指令信号。

由步骤1可知，x1→x1c的前提条件是x2→，由xˉ2通过1个时间常数为τ2的一阶滤波器产生x2c，即

同理，采用ESO2对总扰动项Δωz进行估计，ESO2设计为：

式（17）中：d03＞0；d04＞0；0 ＜λ2＜1；0 ＜h2＜1。

ESO2中的状态z4能够很好地估计Δωz。因此，在控制律设计中将以z4代替式（6）中的Δωz。

对式（15）求导，整理可得，

为了提高复合控制系统的鲁棒性，同时削弱传统滑模控制的抖振现象，采用1 种光滑二阶滑模控制算法[18]来设计控制律。

根据光滑二阶滑模控制的基本原理，只要控制律设计使得误差面s2的动力学满足如下关系式：

式（19）中：p ≥2；k2＞0；k3＞0。

那么，系统状态轨迹将在有限时间内到达滑模面s2=̇=0。

联立式（18）和式（19），求得复合控制量u 的控制律为：

该控制律保证了s2==0 。再由式（15）可得，x2=x2c。此外，由滤波器特性和式（16）可得，当t →∞时，x2c→，由此保证了x2→。这样也就保证了x1→x1c。根据动态面控制的设计原理，复合控制系统的状态量是最终一致有界的。

3 模糊逻辑控制分配算法

由式（20）解算出u 以后，还须要进行控制分配，以产生直接力控制指令和舵偏角控制指令。为了便于分析，将前面式（5）转换为如下的简洁形式：

式（21）中：

利用模糊逻辑控制分配算法解算直接力控制子系统在复合控制系统中占的权重Wrcs（0 ≤Wrcs≤1），而气动力控制子系统所占的权重为1-Wrcs，即：

显然，模糊逻辑系统的输出量是Wrcs。对于模糊逻辑系统的输入量选择问题，考虑到高空的气动力控制效能低，应以直接力为主。因此，选择飞行高度y作为1 个输入量；另外，当过载跟踪误差较大时，需要大的直接力以快速减小误差，提高制导控制精度，因而选择过载跟踪误差的绝对值 ||eny作为另1 个输入量。 y、 ||eny和Wrcs都没有小于0 的情况，定义5 个模糊子集：ZE（零）、PS（正小）、PM（正中）、PB（正大）、PL（特大）。设置 ||eny、y 和Wrcs的隶属度函数分别如图1～3所示。

图1 ||en y 的隶属度函数Fig.1 Membership function of ||en y

图2 y 的隶属度函数Fig.2 Membership function of y

图3 Wrcs 的隶属度函数Fig.3 Membership function of Wrcs

当导弹的飞行高度较高时，或者过载跟踪误差较大时，都应该采用较大的直接力作用以快速减小误差，因而Wrcs应取较大的值，反之，取较小的值。建立模糊逻辑系统输出量规则表（见表1）。

表1 模糊逻辑系统输出量（Wrcs）规则表Tab.1 Fuzzy logic rules table

解模糊化方法采用重心法，模糊逻辑系统的输出量为：

式（24）中：wi为Wrcs的隶属度函数中心；μi为第i 条模糊规则的隶属度，0 ≤μi≤1；n 为模糊规则的总数目。

为了节省能源，避免反作用射流装置频繁开启，对Wrcs设置一定的启动阈值，当Wrcs≤0.2 时，取Wrcs=0。即不开启射流装置。射流装置的喷射阀门采用比例阀，可以提供大小连续变化的直接力。

由式（22）可以解算出：

4 仿真研究

为验证所设计的复合控制系统的控制性能，以某型空空导弹为研究对象开展仿真研究。采用MATLAB 软件M 语言编写了空空导弹复合控制系统的仿真程序，选取导弹在高度14 000 m、飞行速度890 m/s状态下的弹体参数为仿真参数。导弹的舵偏角最大值为30°；直接力最大值为3 500 N，具有连续工作特性。为进行对比分析，既采用基于模糊逻辑控制分配算法的复合控制系统进行了仿真实验，又采用传统的气动力控制系统（设Wrcs始终为0，即u=ua，由气动力承担全部控制作用）进行了仿真实验。仿真设置总扰动项分别为：Δα=0.05 sin(5t) ，Δωz=0.2 sin(8t+π/6) ；过载指令信号为0.2 s 启动的阶跃信号，幅值为20。通过仿真，确定控制参数为：d01=980 ，d02=1 600 ，d03=700 ，d04=1 500 ，λ1=λ2=0.5 ，h1=h2=0.2 ，k1=8.2，τ2=0.04，k2=7.3，k3=3.5。仿真结果分别如图4～7所示。

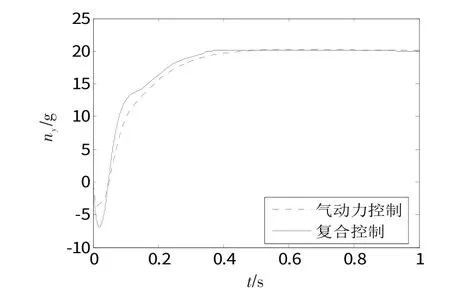
图4 过载跟踪响应曲线Fig.4 Response curve of overload tracking

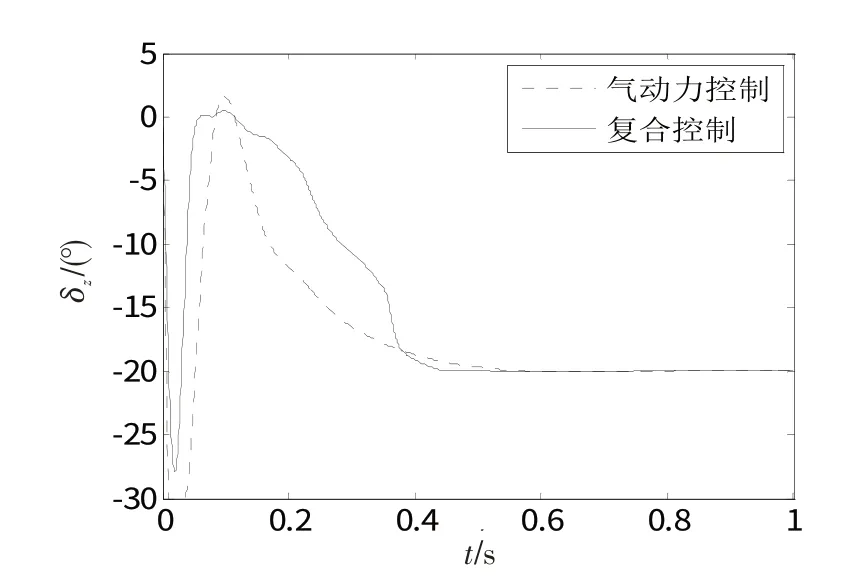
图5舵偏角变化曲线Fig.5 Changing curve of rudder deflection angle

图6 复合控制系统的直接力变化曲线Fig.6 Changing curve of lateral thrust in compound control system

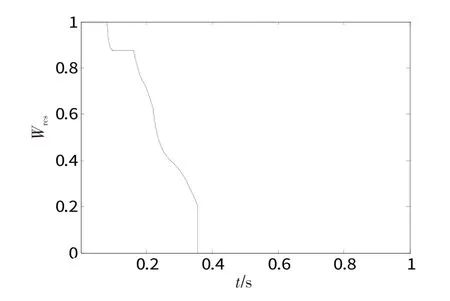
图7 控制分配权重变化曲线Fig.7 Changing curve of control allocation weight

由图4 看出，气动力控制系统的过载响应的上升时间为0.45 s，复合控制系统的过载响应的上升时间为0.36 s，响应快速性提高了20%。这表明所设计的基于模糊逻辑控制分配算法的复合控制系统具有更好的控制效果。由图5、6可看出，2种控制量基本没有抖振现象，展现了光滑二阶滑模控制算法的优越性。

5 结论

本文研究了空空导弹的复合控制系统，采用动态面控制方法设计了复合控制量。在设计过程中，利用了扩张状态观测器估计汇总不确定项，并采用光滑二阶滑模控制算法设计了控制律，有效地削弱了传统滑模控制的抖振现象；设计了一种模糊逻辑控制分配算法，将复合控制量分解为直接力控制指令和舵偏角控制指令。为验证所设计的复合控制系统的控制性能，针对复合控制系统和传统的气动力控制系统进行了对比仿真。仿真结果表明，所设计的基于模糊逻辑控制分配算法的复合控制系统具有更好的控制效果。