基金类别内的确定性等值回报排名次序对风险规避程度的敏感度实证研究

■吴慧明

（上海财经大学）

1 引 言

一个人的风险规避程度属于人格特点，会因人而异。此外Blais et al.的研究发现，同一组人在道德，金融，健康及安全，康乐和社交五个不同领域之间的风险规避程度的差异是他们之中不同人之间的差异的七倍[2]。理论上，投资者所使用的确定性等值回报及其衍生数据不单要吻合自己的风险规避程度，而且具体地是要吻合自己在金融投资领域的风险规避程度，才能发挥最高的参考价值。

有一些测试可以帮助个人对自己在金融领域的风险规避程度作一个量化的评估[1][4]，为使用客制化的确定性等值回报及其衍生数据资讯创造条件。但客制化的确定性等值回报及其衍生数据资讯相对昂贵和较不易得。

财经数据供应商按照典型个人投资者的风险规避程度计算出来的确定性等值回报及其衍生数据资讯就像服装生产商制作出来的量产服装一样，对于部分人来说非常合身，就像量身定做的客制服装一样。但是对于其他人来说就做不到那么合身。这些产品相对较易得和没有那么昂贵。

在恒定相对风险规避效用模型下，当退休基金供款人以比典型的个人投资者较高的风险规避程度去衡量一系列基金，这些基金中的每一个的确定性等值回报都会变得较小。然而它们各自的确定性等值回报由此而来的减量可以不相同。这有可能导致它们之间的确定性等值回报的排名因为风险规避程度增加而有所改变，变得和以典型的个人投资者的风险规避程度去衡量所得的不同。若然退休基金供款人选择退休基金时借用相对易得的为配合典型的个人投资者的需要而按照他们的风险规避程度计算出来的确定性等值回报排名做参考,则理论上有可能会由于背后的风险规避程度不吻合，因不正确的排名而作出不符原意的选择。除此之外，若有基金单位持有人对自己在金融投资领域的风险规避程度缺乏量化了解，甚至可能不知道确定性等值回报随所使用的风险规避程度参数的数值不同而不同，他们也有可能会遇上类似的景况。

本文以2001年1月至2018年1月期间所有中国香港强制性公积金基金的回报历史数据以恒定相对风险规避效用函数以不同的风险规避程度参数数值去求得相应确定性等值回报，以之去探讨确定性等值回报的排名对风险规避程度的敏感度。试图借此对风险规避程度参数数值不吻合会产生什么程度的影响得到一个梗概。

2 在这个实证研究中所采用的基金确定性等值回报计算方法

使用恒定相对风险规避效用函数以回报的历史数据去计算确定性等值回报需要做一些前设。前设的主要目的是为计算中所需的一个概率密度函数能找到一个靠谱的近似代表制造条件。

假设：①某一位投资者的风险规避行为表现符合恒定相对风险规避效用模型；②作为一个随机变数，某一个基金的可能月度回报在过去某个36个月的时段内依从同一个概率密度函数去实现。后一个假设背后隐含的意义是在那36个月内经济环境完全一样，这基金所持有的资产分布完全不变,这些资产各自的盈利能力也完全不变。这样的话，就有理据去用这个基金在那36个月的回报历史数据去近似地代表这时段内这基金的可能月度回报所依从的那一个概率密度函数。

设这个基金在符合后一个假设的期间的某一个月每基金单位的起始资产净值和将得的月末资产净值分别为确定数值w0和随机变量W，对应的月度回报为随机变量R。

如此则有

按照上述前设，这位投资者的风险规避行为表现符合恒定相对风险规避效用模型。所以他的财富的效用由恒定相对风险规避效用函数给出：

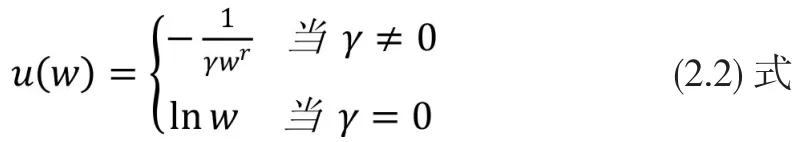
其中：

w代表财富，u(w)代表w的效用。u(w)只定义在w>0的域上。

γ是一个反映这位投资者对这笔投资的风险规避程度的参数。γ>-1代表规避风险，γ数值愈大代表对风险的规避程度愈高。γ=-1代表对风险持中性态度。γ<-1代表喜好风险，γ数值愈负代表对风险的喜好程度愈高。

W的确定性等值wCE定义为与W有相同效用的一个确定财富值。即对于持守既定的γ值的人士而言，带有不确定性的W与全无不确定性的wCE的效用无分轩桎。数学上作为常数的wCE的效用按定义要与作为随机变数的的效用的期望值相等。

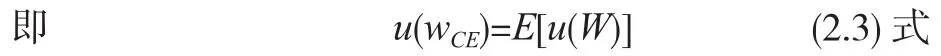
要计算E[u(W)]需要使用W的概率分布函数。一个近似估算W的概率分布函数的常用方法是将W和R由连续随机变量简化为离散随机变量，然后透过R去处理W。以过去36个月的36个月度回报作为R的36个可能结果。每个可能结果的概率均为36分1。

设这月度回报的36个可能结果为r1,r2,…,r36,

对应的每基金单位月末资产净值的可能结果为 w1,w2,…,w36。

由此可得w 的36个可能结果:

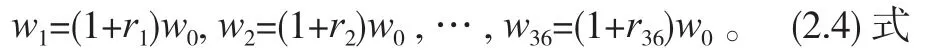
又设wCE的对应回报为rCE。

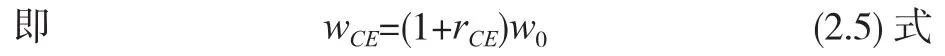
rCE并不是随机变数R的确定性等值。只有财富才可以运用恒定相对风险规避效用函数得到确定性等值。R不是财富。它是一个比率，没有单位的。

基于W和R在(2.1)式里所呈现的关系,W的每个可能结果的概率也均为36分1。于是有

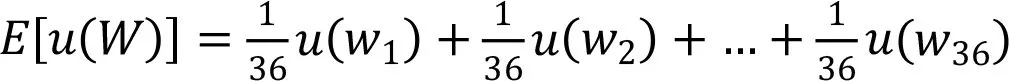
由(2.3)式,

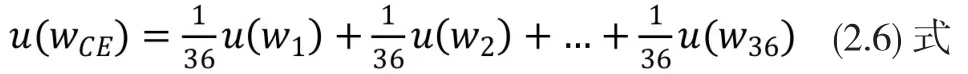
（1）当γ=0的计算

当γ=0,由(2.2)式，u(w)=ln w。

由 (2.6)式,

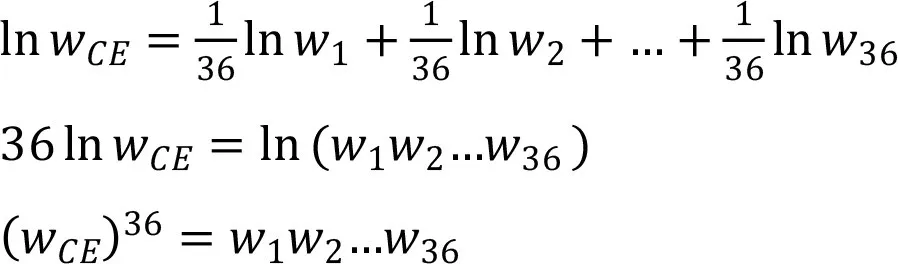
由 (2.4)式和(2.5)式,

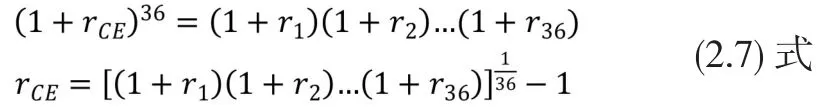
（2）当γ≠0的计算

由 (2.6)式,

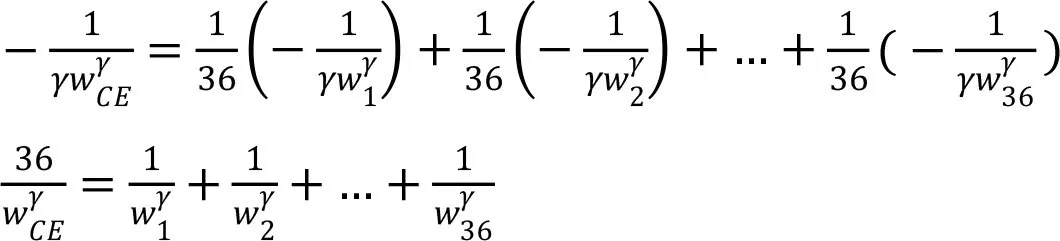
由 (2.4)式和(2.5)式,

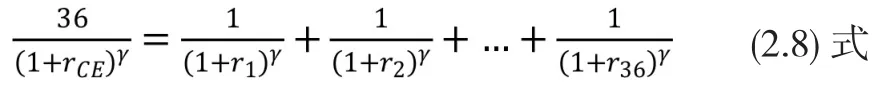
3 研究方法

3.1 研究的焦点在于同类基金之间而非全部基金之间的排名变动

一般来说,为了达到分散投资以减低风险的目的,一个投资组合里面的各个成员基金通常会来自不同的类别。所有获挑选进入投资组合的基金全是在自己的类别里按该投资组合的管理者心中的策略依照一套衡量准则量出来的最适者。这套准则衡量的项目往往会包括确定性等值回报。

不同的人在金融投资方面可以持不同的γ数值。由(2.2)式可知，以不同的γ值作计算所得的确定性等值回报会有所不同。因为最广泛流传的基金确定性等值回报的排名讯息通常是按照典型的个人投资者的γ值计算所得，所以会和按照典型的退休基金供款人的γ值计算所得的版本有差别。

这次研究的目标就是要知道，在同一个类别里的基金的确定性等值回报排名的次序在不同的γ值下的差别有多显著。其目的就是为了知道当典型的退休基金供款人借用了为典型的个人投资者制作的确定性等值回报排名作为类别内基金之间进行比较的其中一个指标时，问题大不大。

因此这次研究的焦点并不在于基金的总排名的变动，而是在于同类基金的类别内排名的变动。基于上述原因，在研究程序当中会先将研究对象基金依其特性归类，然后再就每一类去观察基金在类内的排名受γ值变动影响的程度有多大。

3.2 研究所涵盖的γ值变动范围

在研究程序中γ值由-1以每次增加0.1的步伐上升到4。基于典型的个人投资者的γ值为2[3]，对风险抱持中性态度的投资者的γ值为-1，这个γ值变动范围涵盖了由对风险抱持中性态度者，到典型的个人投资者，再到风险规避程度较高者的变化。

3.3 选择一个指标去反映一个类别发生类别内排名交换的频密程度

每当γ值上升，类别内的基金的确定性等值回报就全都会下降，但下降的数值各有不同。

就类别内任意一对基金观察，假使在γ=-1 时它们的确定性等值回报一高一低，但若它们的下降速度是高的快低的慢，则有可能当γ值上升到某一数值时原本较高的一个会跌至比原本较低的一个更低。这样两者的排名就交换了。

排名的交换有可能影响到数据使用者对基金的选择，所以它发生的次数是本文的关注点之一。然而研究排名交换次数的最终目的是要研究类别对γ值变动的敏感度。基于即使两个类别对γ值变动有相同的敏感度，基金数目较多的一个类别发生的排名交换还是会较多，所以以类别内排名交换的次数除以类别内的有排名的基金的数目作为频密程度指标较为合适。在相关月份营运未足连续36个月的基金未能有回报的3年期确定性等值回报，故此不会有相关排名。再考虑到较宽的γ值变动范围也会有较大的排名交换次数，所以以类别内排名交换的次数除以类别内有排名的基金数目再除以γ值改变范围的宽度作为频密程度指标更为合适。

所以本文选择以类别内平均一个有排名的基金每单位γ值变化产生的类别内排名交换次数作为该类别的排名交换频密程度指标。若一个类别有较高的排名交换频密程度指标，显示这个类别对γ值变动有较高的敏感度。

3.4 尝试了解每一个类别的排名交换频密程度指标的概率分布

就每一个类别而言，可以从研究期内所有月份的每单位γ值变化产生的排名交换的频密程度指标数值的算术平均，样本标准差和算术平均的标准误差,得以窥探该类别的指标数值的概率分布。研究所覆盖的时段内营运期最长的类别有170个指标数值可作统计之用。不同类别的敏感度的差异可以透过这些统计数值得到恰当的比较。

4 执行实证研究

4.1 选取研究对象

基于关注强制性公积金供款人若不知就里地采用了基于典型的个人投资者的风险规避程度计算而得的确定性等值回报排名所产生的差别是否严重，本文将研究对象范围界定为所有在营运中的中国香港强制性公积金。

4.2 研究所用数据

测试会用到相关基金的月度超额回报数据。其中超额的意思是超出无风险回报的回报额度，是比无须承受风险也能得到的回报多出的部分的意思。它们反映了基金单位价格升跌，加上派息的效应，并扣减了无风险回报。数据所覆盖的时段为2001年1月至2018年1月。研究数据中的基金共分为19类。

4.3 研究操作

以下是就每一个γ值区间所作的排名交换频密度指标计算。

为19个基金类别逐一执行以下步骤：

为确定性等值回报研究期内每一个月逐一执行以下三个步骤：

步骤1：为类别以内每一个基金以(2.7)式或(2.8)式按照γ值由指定区间的左边界开始，以每次加大0.1的步伐上升至区间的右边界时，逐一算出其确定性等值回报。例如当区间为-1至4，则要分别计算出γ=-1,-0.9,-0.8,...,3.9,4 时的确定性等值回报。

步骤2：为类别以内每一对基金检查以上列出的每两个相邻的γ值的相应两对确定性等值回报有没有出现大小交换的情况，并累计该类别的总交换次数。

步骤3：将该类别该月份的总交换次数除以该类别在该月份有排名的基金数目再除以该γ值区间的宽度得出该类别在该月份在该γ值区间每单位γ值变化产生的排名交换频密程度指标。

将研究期内所有170个月末的该类别的指标数值求算术平均，样本标准差以及样本平均值的标准误差。

步骤完。

5 研究结果

上述4.3的操作结果列在表5.1内。

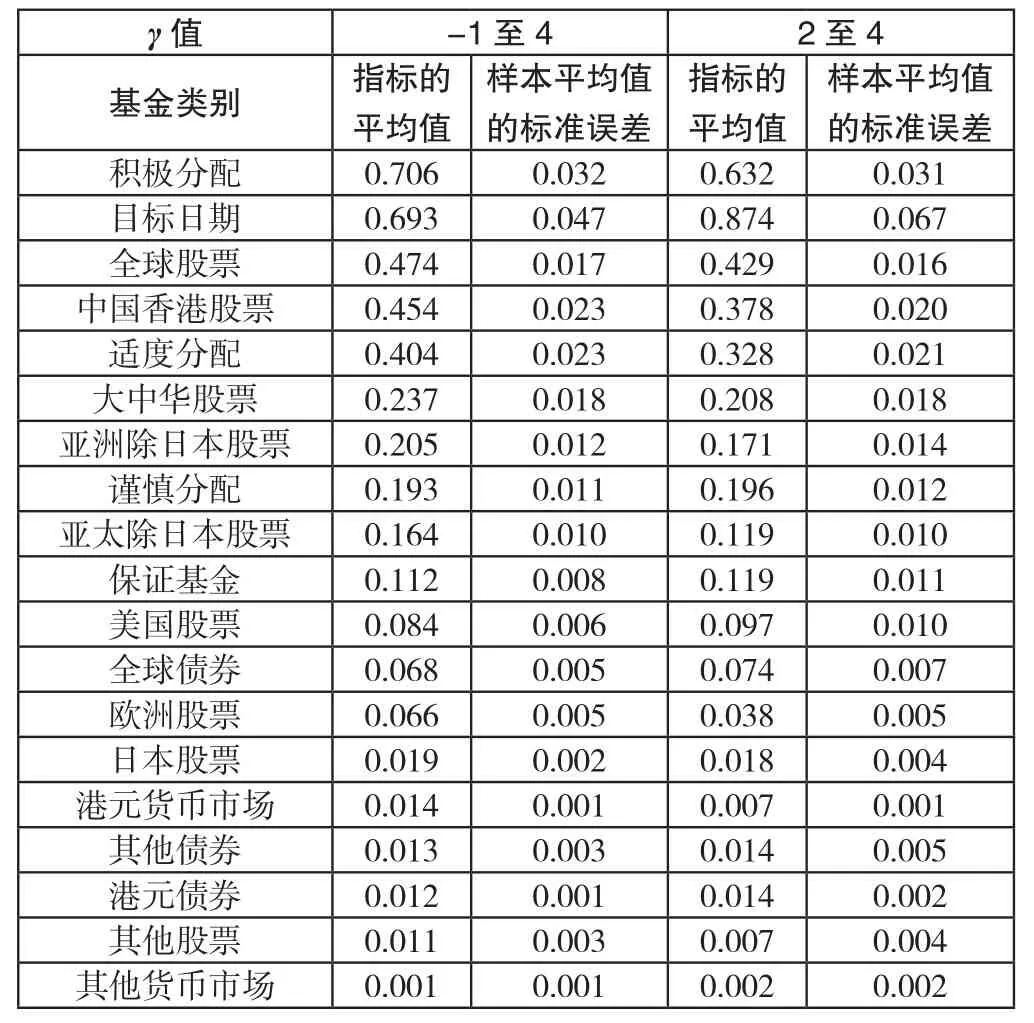
表1 各类别在不同覆盖范围的区间上排名交换频密程度指标的算术平均和样本平均值的标准误差＊

类别的排名交换频密程度指标定义为该类别内平均一个有排名的基金每单位γ值变化产生的类别内排名交换次数。可见在指标的定义里已经就区域宽度的差异设置了相应的调节机制使之适合用作比较。

（1）由表5.1所见,按基金所投资的市场观察，投资在股票市场的基金类别的排名交换频密程度指标一般偏高，而投资在债券或货币市场的基金类别的排名交换频密程度指标一般偏低。

（2）不同基金类别的排名交换频密程度指标之间的差别相当大。以风险规避参数γ的数值由-1增加到4的区间而言，排名交换频密程度指标平均值处于最高,中位数和最低的基金类别分别是“积极分配”“保证基金”和“其他货币市场”。这三个基金类别的排名交换频密程度指标平均值取5位有效数字时的值分别是0.70577,0.11196和0.00072。位处最高的是位处中位数的6.3倍。位处中位数的是位处最低的156倍。位处最高的更是位处最低的980倍。

（3）从关注强制性公积金供款人借用为典型的个人投资者所计算的类别内排名的可行性的角度出发，检视在 γ值由2增加到4的区间内各个基金类别的指标数值，会留意到以“目标日期”类别为最高，其指标数值达到0.874。这个指标数值可以这样理解：假若在这期间的某一个月“目标日期”类别内有10个基金能有3年期确定性等值回报排名，则在γ值由2增加到4的过程中,平均说来在“目标日期”类别内的10个有排名的基金之间共发生了约等于 (类别指标×基金数目×区间宽度)=0.874×10×2次排名交换。

这个指标数字背后所发生的事情构成一个可能性光谱。光谱的其中一端是少数基金的排名出现了重大的差别，例如在10个基金之中有2个在γ值分别等于2和4时各自出现了排名相差8至9位的差别。光谱的另外一端是大多数基金的排名出现了小差别，例如在10个基金之中有8个出现了排名相差2位，另外2个出现了排名相差1位的差别。因为17.84次只是个平均数，所以以上描述的只是平均情况的情景。当统计上较低可能性的情况出现，例如某一次的次数实际上是24次或12次，则相应的极端情况可以变得更极端，达到10个基金之中有3个基金各自出现了排名相差7，8和9位的差别，或10个基金之中只有2个出现了排名相差2位，其余8个出现了排名相差1位的差别。

假若一位γ值为4的强制性公积金供款人要为是否借用为典型个人投资者以γ等于2计算出来的“目标日期”类别的排名资讯作一个知情选择，他先得知道平均说来他要面对以上程度的排名差异。

（4）在19个类别当中的16个在整个研究期间或接近整个研究期间都有营运，所以他们每一个都有170个或接近170个指标数值可以用作估算该类别的指标的概率分布的均值，和样本均值的标准误差。其余的三个类别分别有76，41和31个指标数值可作此用。由表5.1所见,各个类别的样本均值的标准误差比起样本均值都不算大。所以这些样本均值都适合用作估算对应类别的指标的概率分布的均值。

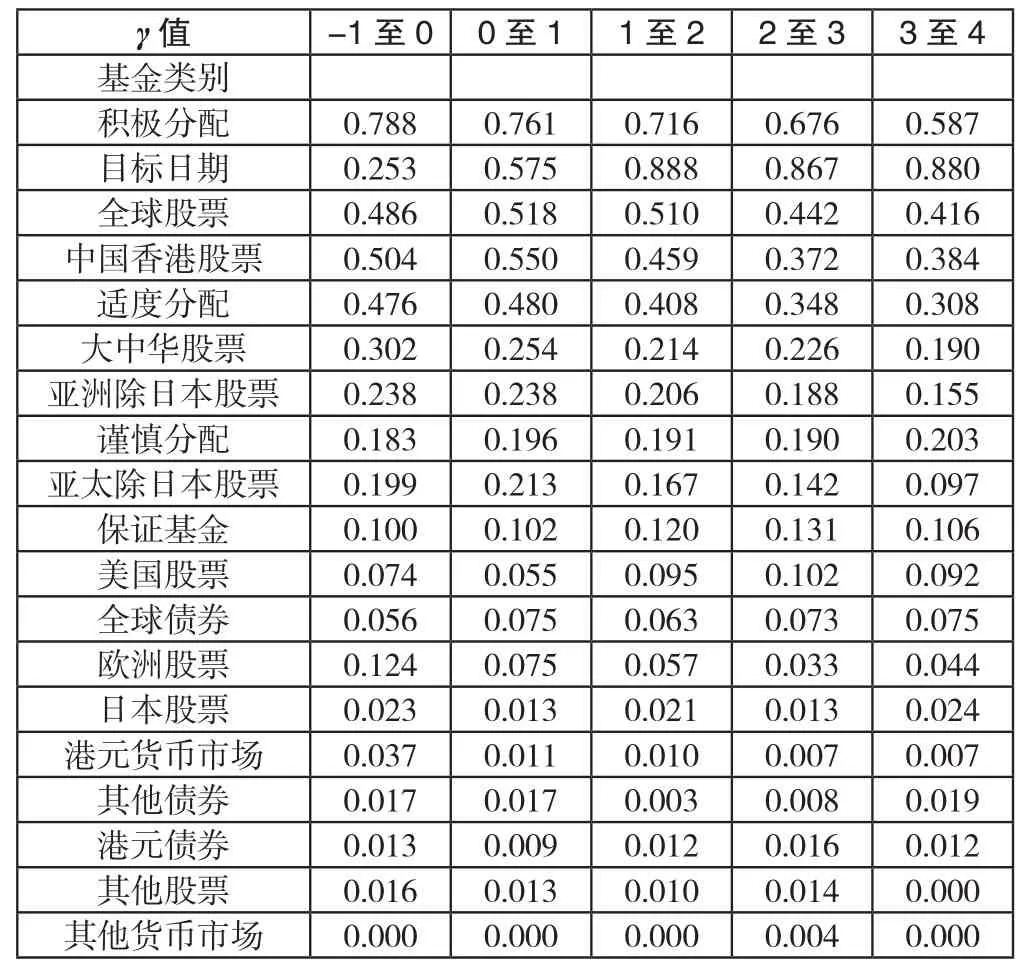
表2 各类别在相邻单位宽度区间上排名交换频密程度指标的算术平均

（5）当检视γ值上升的不同阶段,由表5.2所见，从γ值由-1至4的区间分拆而成的5个宽度为1的子区间当中，并没有哪一个子区间明显表现出通常有较高排名交换平均数的倾向。

6 研究的局限性

本文以一个基金的类别内每单位γ值变化产生的平均一个基金的排名交换的次数作为该类别的频密程度指标。然而这个指标的参考价值是有它先天的局限性的。作为一个平均数,反映对象群体内的个别差异会是它相对较弱的一环。群体的平均数的数值并没有描述群体内部某一个体数值的能力。

例如以下的说法就不成立：

“凡是在γ值由a上升到b的过程中类别内排名交换的平均次数高于1次的类别，它在γ值是a时排名第一的基金,在γ值上升至b时都有相当确实的机会发生过一次或以上排名交换因而有很大机会不再排名第一了。所以γ值是b的人在这种类别里一定不能借用为γ值是a的人所计算的确定性等值回报资讯去寻找类别内最高确定性等值回报的基金，因为对他们来说这样找到的不是最高的一个。”

理据可以从以下这个虚拟情景找到：

在本月所发报的数据当中,某个类别的基金之中有十个基金有其回报的3年期确定性等值回报数据。在γ值由-1上升到4的过程中,这十个基金的确定性等值回报随γ的改变如图1中的图线所示。

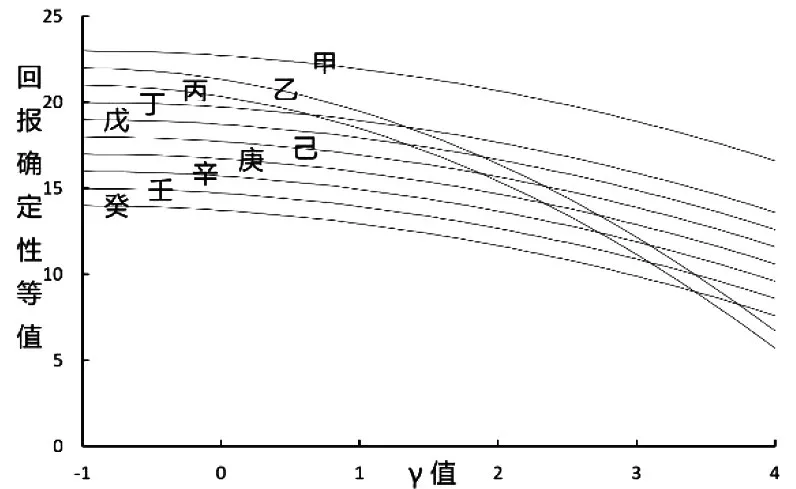
图1 十个基金确定性等值回报随γ的上升而下降,但速度的差异引起排名交换

在γ值等于-1时，基金甲乙丙丁戊己庚辛壬癸分别排名第一至第十。

在γ值由-1上升到4的过程中，基金甲一直保持排名第一；基金丁至基金癸七个的排名相互之间维持相同的次序一直没有交换过; 基金乙和基金丙两者之间的排名也维持相同的先后次序一直没有交换过。

不过基金乙和基金丙的γ值持续同步快速下跌。在γ值等于4时，基金乙和基金丙的确定性等值回报都已逐一跌过了基金丁至基金癸七个的数值。他们的排名已经分别跌至第九和第十，各自作出了七次排名交换。

在这个虚拟情境中，这个类别发生过14次确定性等值回报类别内排名交换。平均一个基金的交换次数是1.4次。但基金甲的类别内排名交换次数没有如以上的说法推断那般变成1次,而是确确实实维持在0次，依然排名第一。平均数是1.4与其中一个数值是0没有矛盾。因为群体的平均数的数值并没有描述群体内部某一个体数值的能力。这是以平均交换次数作为指标的先天局限性。

上述指标是对整个类别而言的。一个类别的指标数值较高，只表示类别内基金排名受γ值变动导致的总体变动较大，但并不指明某一基金的排名变动一定大。

7 结 论

本文提出了一个反映一个基金类别里确定性等值回报的排名次序对风险规避程度的敏感度的指标，并分析了这个指标的局限性。本文以历史数据为一个地区的强制性公积金提供了上述指标数值。

按照上面所得的数据结果，本文觉得使用按照典型个人投资者的风险规避程度计算所得的确定性等值回报资讯就和穿着量产服装相似: 产品不一定是最理想的，但也不至于完全不可用；和理想版本可以有的差别大小因类别而异。消费者意识到存在差别的可能性，作一个知情选择就可以了。而本文所得的数据结果可以为这个选择提供初步参考。