精准定位提升数学思考力
【摘 要】实际体验会给人留下深刻的印象。有所体验,就会有所感悟,有感悟就会产生思考,有思考才能培养数学思想。“找次品”是人教版五年级下册“数学广角”单元的教学内容,是经典的数学思维课例,可以作为教学研讨内容。
【关键词】小学数学;体验;经历;思维
“找次品”是人教版数学五年级下册“数学广角”单元的内容,作为经典的数学思维课例,经常成为教学研讨的内容。笔者听过多次这一节课的内容,也进行了多次教学实践,对此总结如下。
1 存在的问题
(1)目标不明确。这节课综合了很多的教学内容,包括学生的操作与观察、猜想与验证、归纳与推理等活动,既要实现解决问题的多样性,又要体现解决问题时优化思想的渗透;既要让学生体验和经历规律的形成过程,又要实现学生解决问题能力的提升[2]。但是由于内在规律的隐蔽性,一节课下来,学生常一头雾水,教师也头昏脑涨。
(2)学生思维停留在表面。整堂课的内容很多,学生应该要学些什么?一些教师认为这节课的重点是落实优化策略,于是整堂课就在讨论该如何解决问题,每讨论一个总物品数就把它所有的分法和次数都讲一遍,最后得到一个最简便的[3]。还有教师觉得必须做一个表,让学生观察和发现。尽管学生和教师都忙得不可开交,但效果不尽如人意。
(3)教师对教材的理解不够透彻。有教师对“找次品”问题的思想方法说不清道不明,只知道“尽可能平均分成3份”,那么为什么要分3份呢?能不能分成4份呢?为什么有时候平均分2份和平均分3份是一样的呢?它们有区别吗?对于这些延伸问题,这些教师都没有讲清楚。
(4)不理解天平的作用。天平的作用是什么?是用来称重量的,还是用来比较物品重量的?教师不能限制学生的思维,要让学生暴露出原有的思维状态[4]。在学生的观念中,天平是用来称重量的。教师很有必要让学生改变这样的观念,让学生明白天平其实就是一个等臂杠杆。
2 教学实践与思考
2.1 只有激发认知冲突,才能产生问题
对于这节课的导入,大多是以任务驱动为主。如有的教师是这样导入课堂的:“81个小球中,有一个稍重的小球,如果利用没有砝码的天平,你至少要称几次才能保证找到那个稍重的小球?猜一猜,并说一说理由。”笔者认为,问题模型中出现的两个词语“至少”和“保证”,可能不利于学生理解和接受,所以应该设计更加合适的课堂导入语。
为此,笔着设计了这样的问题:“在一个装有500多个小球的池子里,有一个小球略重,你能保证找到它吗?”笔者的思路如下。第一,“500多个”是一个大概数,它能更好地体现区间量。第二,可以让学生理解“保证”这个词语的意思。笔者提出问题后,有的学生回答:“可以用秤称一称。”对此有的学生说:“这样太慢了。”有的学生说:“老师,这里的球太多了。”有的学生说:“运气好的话,称两次就可以了。”然后笔者引出“保证”的意思从运气最差的方面考虑(最不利原则)。师生共同分析得出:需要一个合适的工具,以提高效率,尽快找到那个略重的小球。由此引出“天平”。之后笔者向学生介绍了天平的使用方法。在两边的托盘中放入相同个数的小球后,会出现两种情况,让学生说出次品在哪儿,然后提出“化繁为简”,从2个开始研究。
2.2 只有经历“举三反一”,才能发现规律的存在
在教学这节课之前,笔者听了很多教师的课,也看了很多文章。其中有一个共同点:这节课一定要学生学会把物品分成3份。那么为什么呢?在教学6个的时候,把6分成(3,3)和(2,2,2)都是能保证找到次品的,怎么解释呢?要解释吗?这些知识只可意会不可言传,因此,要寻找一个恰当的时机开展教学。
在8个小球中找次品是一个很好的时机。因为(4,4)和(3,3,2)在次数上是不同的。要让学生自己体会到平均分两份的局限性。教师不应该在这个阶段去干预学生的思考,让学生匆忙下结论。因为这是学生通过长期形成的思维习惯得出的。
应该让学生保持懷疑的态度,应该用学生之间的探讨和研究代替教师的引导[5]。要让学生自己找证据,用实实在在的例子说明。可以研究“9”的至少次数。让学生发现从9个中找一个次品至少需要2次,这时学生肯定会产生怀疑。让学生自觉地发现问题,然后找出证据说明。这个时候,可以回到从6个中找一个次品,学生会发现平均分3份并没有什么优势。由此引发学生进一步去找证据说明。让学生探究总数是16个、20个等偶数个的情况,在尝试和对比、分析中达到真正的优化。一次优化的过程其实是一次头脑风暴,必须是彻底的觉悟,而并不是简单的告知。
2.3 突出最值的重要性,体现思维的严密性
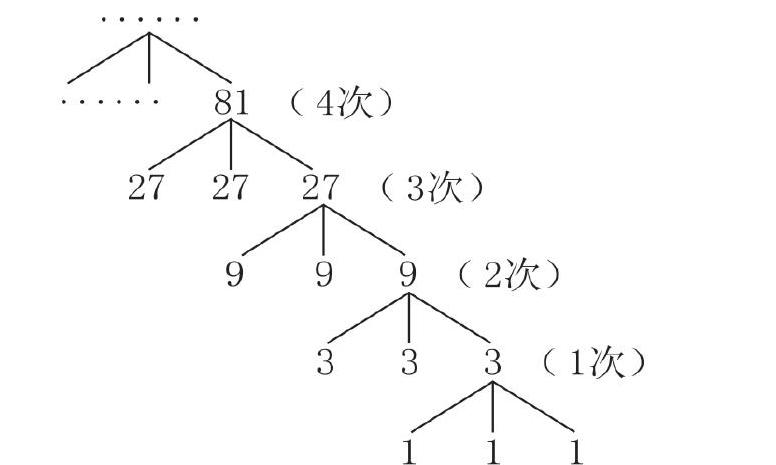
当教学完在2个、3个、4个里找次品之后,教师可以提出:“2个和3个小球中找略重的小球只要1次就能找到,从4个小球中找要2次才能找到。这说明用天平称一次可以最多在几个小球里找到次品呢?”然后,可以让学生猜测和验证用天平称2次、3次可以最多在几个小球里找到略重的小球。在探究的过程中,可以结合如下思维导图。
借助思维导图,要让学生理解要找到的一定是次品,那么其余两份最多是1个和1个,因为称1次最多能在3个物品中找到次品。那么最大范围,只能定在3个,因此其余两份也就最多是3个和3个,依此类推。
由此可见,优化思维必须通过一系列的思维活动,只有让学生真正感受到一种迫切的需要,才能让学生的思维走向深入。透过现象看本质的本领不是一朝一夕就能练成的,需要教师不断探索。为了在课堂中渗透数学思维,教师要精心设计教学过程,在教学中体现思维的逻辑性和严密性。只有这样,才能让数学思想真正融入学生的思维之中。
【参考文献】
[1]华应龙,刘伟男.从一分为二到一分为三——以找次品教学为例[J].小学数学教师,2015(10).
[2]王广丽.对一类“找次品”问题的探讨及其教学建议[J].新课程研究,2008(9).
[3]陈沙,王美德.感受数学优化思想的魅力——“找次品”教学实录与评析[J].小学数学教育,2014(3).
[4]王桂清,赵顺天.让学生经历探索,去感悟模型魅力——以 “找次品”教学为例[J].新教师,2015(5).
[5]林碧英,陈秀娟.直面难点巧妙设计——找次品教学实践与思考[J].小学数学教师,2018(4).
【作者简介】
邱伟星(1978~),汉,本科。研究方向:小学数学。

