浅谈高等数学中的思想方法及其教学建议
■张芙敏
(浙江东方职业技术学院)
数学是一门非常重要的学科,它与人类的生活和发展密不可分,社会主义现代化建设的各行各业都需要数学。认识数学、研究数学、应用数学到什么程度,主要看人们对数学思想方法掌握得怎么样。[1]数学的显性知识点如概念、定理、公式等可能会随着时间的推移被淡忘,但基于显性知识的数学思想方法它将化为内生知识可随时随地发生作用。数学思想方法对人的能力的培养及素质的提高都具有非常重要的作用。因此在高职高等数学教学中,我们应加强渗透数学思想方法的教学。
1 高等数学中数学思想方法的主要内容
所谓“思想”是:客观存在反映在人的意识中经过思维活动而产生的结果。而“方法”是:关于解决思想、说法、行动等问题的门路、程序等。
数学思想方法是人们对数学内容本质的认识,是对数学知识的抽象与概括,属于对数学规律的理性认识的范畴[2]。
高职《高等数学》教学内容主要包含函数与极限,导数与微分,导数的应用,不定积分、定积分、定积分的应用等。其中的数学思想方法可分为三类:一是思想观点类。如:函数思想,极限思想,转化思想,方程思想,数形结合思想等。二是思维方法类。如:猜想,归纳(从特殊到一般),分析与综合,抽象与概括,观察,类比,演绎与证明等等。三是技能技巧类。如:换元法,配方法,待定系数法,有理化,坐标法等等。
2 高等数学教学过程中渗透数学思想方法教学的建议
在高等数学教学过程中数学思想方法教学是一项长期且需不断挖掘的工作,需要教师们不断总结、学习、分享。如何在高数教学过程中渗透数学思想方法,笔者认为应做到以下几点。
2.1 教师在思想上应重视数学思想方法教学
只有思想重视,才有行动支持。数学知识,如概念、定理、公式,都明显地写在教科书上,大纲有要求,肯定不会被忽视,而数学思想方法是隐于知识教学过程中,教学大纲考纲都不会被呈现,容易被忽视甚至忽略。所以教师只有在思想上重视数学思想方法教学,才会在教学过程中渗透数学思想方法教学。
教师在备课时可注意该知识点相关的数学思想方法,并从教材中不断挖掘、提炼,并将该知识点涉及的数学思想方法与该知识点一同纳入教学目标中,这样在做教学设计时必会设计好渗透数学思想方法的教学。
如在讲导数的概念时,教师不仅要解决函数在某一点的导数“是什么”的问题,更要解决的是“是怎样想到的”问题及在概念形成过程中所体现的极限思想。如导数定义引例中一例子。
已知自由落体运动的路程s与所经过的时间t的关系是:
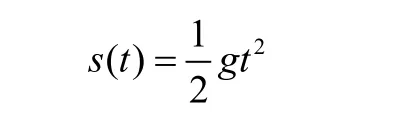
求:(1)3秒到3+Δt秒的平均速度;
(2)3秒时的瞬时速度。
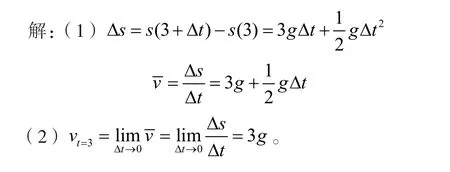
在解该题时,教师不能只满足解出题目结果,而应将它的3秒时的瞬时速度如何实现等于3秒到3+Δt 秒的平均速度的这个思维过程传给学生,也就是其中涉及的极限思想得让学生感受到。
2.2 教师在教学中应注意数学思想方法教学的反复性
数学思想方法尤其是思想观点类的,它具有高度的抽象性,没有固定的形式,有时只是一种思想意识,它需要教师反复渗透,不断让学生体会,才能逐渐被学生掌握。因此,教师在教学过程中,当遇到类似数学思想方法时,应不失时机地告诉学生,让学生不断体会,领悟,深化,才能达到有意地,自觉地应用此思想方法。
例如前面提到的极限思想,当讲到定积分的概念时,又会涉及。教师应抓住时机,让学生再次体会、领悟。如:
【例2】 求曲边梯形的面积。
解题主要过程:(1)分割——分曲边梯形为n个小曲边梯形
(2)近似代替——用小矩形的面积代替小曲边梯形的面积
(3)求和——求n个小矩形面积之和
(4)取极限——由近似值过渡到精确值
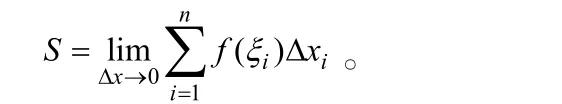
其第四步就涉及极限思想,在讲到该点时,要注意让学生体会、领悟极限思想。当然,此时已是第二次讲到该思想方法,教师在教案设计时要注意以引导为主,让学生自己想到此思想方法,培养学生潜意识里会应用此思想方法的能力。
2.3 教师在教学中应注意数学思想方法教学的系统性
数学思想方法教学的系统性需从纵横两个方面去把握:纵向是这一数学思想方法在教学过程中可以借助哪些知识点来渗透;横向是这一数学知识点可以进行哪些数学思想方法的渗透。教师在教学中应注意从纵横两个方面对数学思想方法教学进行系统研究,从而能循序渐有的放矢的让学生掌握相应的数学思想方法。下面以纵向为例。比如构造函数思想,它是一种重要的数学思想方法,在高等数学解题中经常用到。高等数学教学中涉及该思想方法的有以下几个知识点:
(1)零值定理。
如:【例3】证明方程x5-3x+1=0在区间(0,1)内至少有一个根。
证明:令f(x)=x5-3x+1,则f(x)在[0,1]上连续。
又f (0) =1,f (1) =-1,
根据零值定理,有ξ∈(0,1)使f(ξ)= 0。
即 方程x5-3x+1 = 0在区间(0,1)内至少有一个根ξ。
(2)最值问题——最小成本最大利润问题。
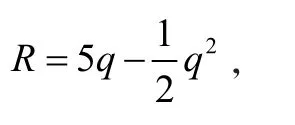

教师只有清晰课程中数学思想方法的系统内容,才能在教学过程中更加自如地渗透数学思想方法的教学。
总之,数学思想方法是以数学知识点为基础又高于数学知识点的一类隐性的数学知识。数学思想方法教学的重要性也已被越来越多的教学工作者们所重视。如何在教学中渗透数学思想方法仍是一个任重道远的重要课题,需要广大教学工作者们投入更多的时间和精力去共同探讨和研究。

