基于锥形透镜的光线入射角度测量系统设计与研究

（中国科学技术大学 精密机械与精密仪器系，安徽 合肥 230026）

引言

光线入射角度的测量在机械制造、测试计量和精密仪器等领域具有广泛的应用。例如主要由光电探测器、步进电机跟踪模块、电路模块等组成的可用来提高太阳能利用率的太阳光角度追踪器[1]；主要由光学镜头、图像传感器以及图像处理系统组成的对卫星进行姿态测量的恒星敏感器[2]以及应用于目标探测领域的目标跟踪系统[3]等。目前，在光学测量领域，尤其是光线入射角度的测量，大多采用光电探测法来实现。光电探测法通常在特殊结构上布置一定数量的光敏元件，光线入射角不同时会导通不同的光敏元件组合，进而确定光线角度。但这种方法需要较多的光敏元件，调试工作量大。还有通过测量不同位置光电池的输出短路电流来计算入射光角度。这种方法虽然可减少光敏元件的数量，但光电池特性不一致或特性变化时则会导致较大的误差[4]。此外还有采用微透镜阵列进行光线入射角度测量的方案，比如通过至少一组具有预先规划安装参数的微透镜阵列实现光线角度的测量[5]，但此类方案也存在微透镜阵列较多，一致性难以保证，安装调试工作量较大的缺点。本文提出一种基于锥形透镜[6-8]的光线入射角度测量系统与方法，利用光阑、锥形透镜和图像接收装置，获取待测光线通过光阑射入锥形透镜后在图像传感器得到的光斑图像，通过图像处理得到光斑图像特征信息，进而结合标定数据求解光线入射角度。该方法具有精度高、成本低、结构简单、体积小、功耗低等优点。

1 系统介绍

如图1所示，本系统中包括光阑、锥形透镜、图像接收装置、图像显示装置以及图像处理装置。待测光线经过光阑至锥形透镜大端端面射入锥形透镜，以不同角度入射的待测光线，会在锥形透镜中发生不同次数的全反射，全反射次数越多入射角越大，当入射锥形透镜侧壁的光线不满足全反射条件时，光线从锥形透镜侧壁射出，射出的光线被图像传感器接收并形成图形化的光斑图像；由于出射光束的边界由临界全反射角确定，因此光斑图形有着清晰的边界，易于通过图像处理提取出光斑图像的特征信息，进而求解出待测光线的入射角度。

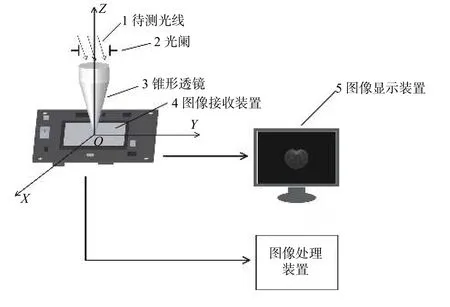
图1 系统结构示意图Fig.1 Schematic diagram of system structure

系统包括光阑、图像接收装置、图像处理以及锥形透镜四个部分。

1）光阑

光阑放置于锥形透镜大端表面或上方，并且与锥形透镜同轴放置；光阑形状为圆形或环形通孔，尺寸小于等于锥形透镜大端口径。

2）图像接收装置

图像接收装置主要用于获取待测光线经由锥形透镜所形成的图形化光斑图像，待测光线在锥形透镜内经一次或多次全反射，最终会从锥形透镜侧壁出射并照射到图像传感面，形成光斑图像。

3）图像处理

提取出光斑图像的特征信息后，结合锥形透镜光学参数和几何参数、光阑尺寸与位置、以及标定数据，计算待测光线入射角度。具体计算时，可以先通过标定将入射光线的角度与光斑图像的特征信息一一对应，接着通过图像处理方法求解图像接收装置获取的经由锥形透镜形成的光斑图像的特征信息。最后将图像的特征信息与标定数据比对或进行插值运算，从而精确地测出待测光线的入射角度。

4）锥形透镜

图2（a）为锥形透镜的示意图。锥形透镜的参数包括材料折射率、大端口径以及锥角，材料可以是各种透明材料，应用的范围不限于可见光。锥形透镜放置的方向垂直于图像传感器接收面且尖端接触或靠近图像传感面。

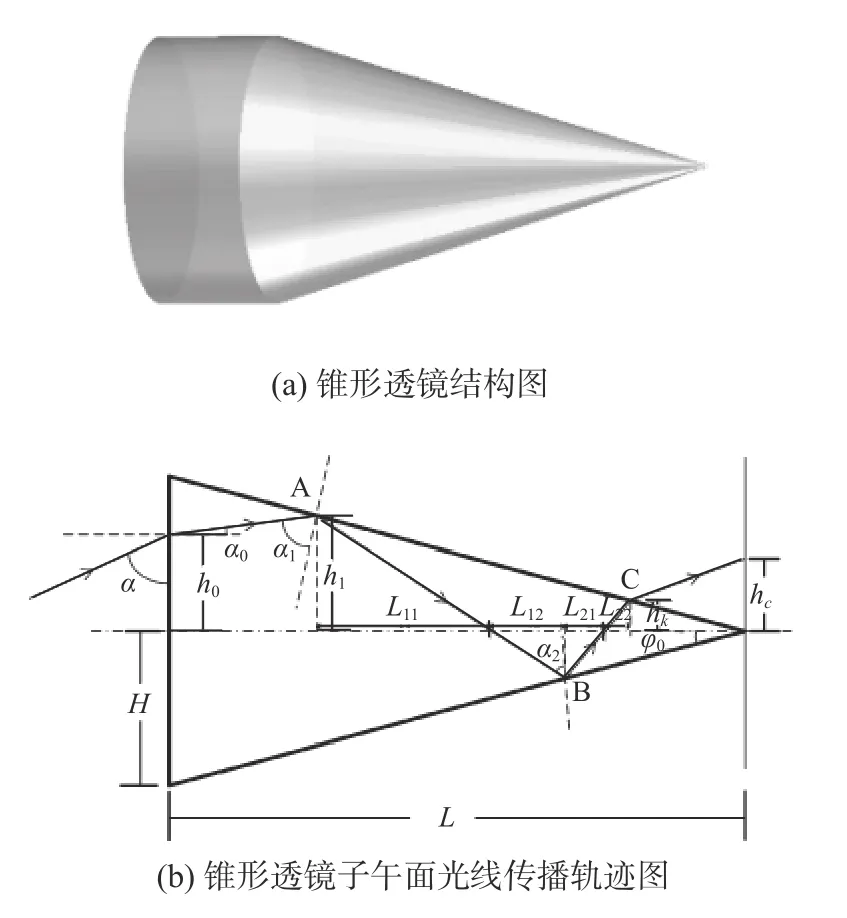
图2 锥形透镜模型及子午面光线传播轨迹图Fig.2 Conical lens model and its’ ray trajectory in meridional plane

锥形透镜的参数、光阑位置和尺寸以及待测光线入射角度决定了图像接收装置接收面上光斑图像的尺寸和形状；当待测光线平行于光轴入射时，光斑图像尺寸最小且图像具有圆对称结构，当待测光线与光轴夹角增大时，由于子午光线在面内全反射状态和非子午面的斜面全反射状态不同，使总体出射光束形成的光斑尺寸增大并具有不均匀性的轴对称结构，因此，可以提取出多种图像特征。

如图2（b）所示为光线在锥形透镜子午面内传播的光线轨迹图[9]。现假设光阑放置在锥形透镜的大端端面处，假设光线以 α角度从锥形透镜的大端端面入射时，光线的折射角为α0，在锥形透镜内入射光线与锥形透镜壁法线方向的夹角为αk，其中k表示第k次全反射，锥形透镜材料的折射率为n。则根据几何关系可知：

式中：k=2,3,4,······

当光线第一次入射至子午面上侧壁时，

当光线第一次入射至子午面下侧壁时，

又根据光的折射定律，当锥形透镜放置在空气中时，

因此，当光线第一次入射至子午面上侧壁时，反射角之间满足关系：

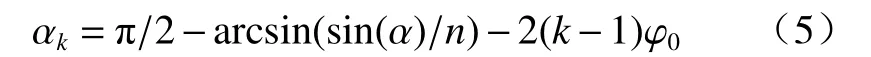
当光线第一次入射至子午面下侧壁时，反射角之间满足关系：

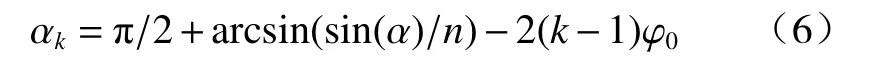
通过上述公式可以看出，光线每反射一次，入射角就减小一个锥形透镜锥角。锥形透镜的全反射临界角θ=arcsin(1/n)，当光线经过多次全反射后，光线的入射角逐次减小，当减小至小于全反射临界角时，光线在锥形透镜侧壁发生折射并射出锥形透镜。根据这一特性，可以先求出光线在锥形透镜内全反射次数。

考察子午面上出射光线位置与光线入射角关系有助于理解光斑图形形状变化。假设光线第k次全反射时在锥形透镜内的高度为hk，光线在锥形透镜侧壁发生第一次全反射后，从A点到B点沿锥形透镜轴向方向前进的距离为

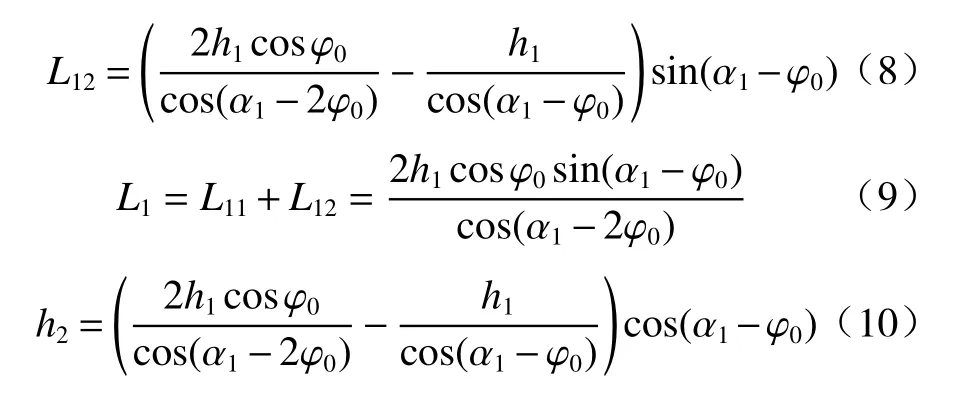
同理，光线从B点到C点沿锥形透镜轴向方向前进的距离为

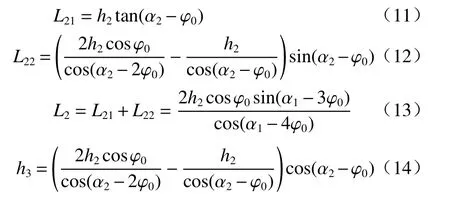
光线在锥形透镜内发生多次全反射不断前进，根据在|AB|和|BC|两个反射点之间前进的距离公式，可以推出光线在锥形透镜内两次全反射之间前进的距离公式为

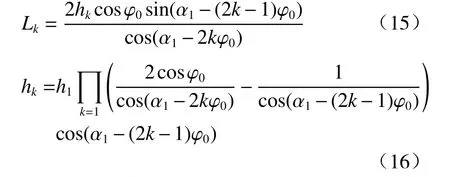
现以h0表示待测光线在锥形透镜大端端面入射的高度，H表示锥形透镜大端端面半径，则当光线入射锥形透镜上侧壁时，

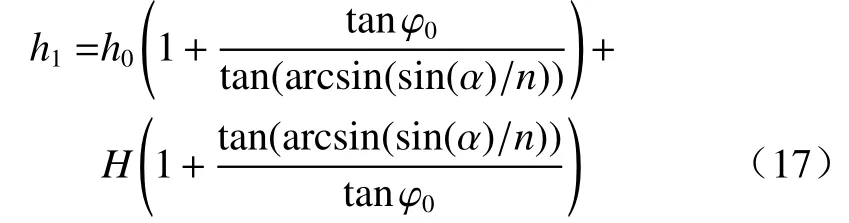
当光线入射锥形透镜下侧壁时，

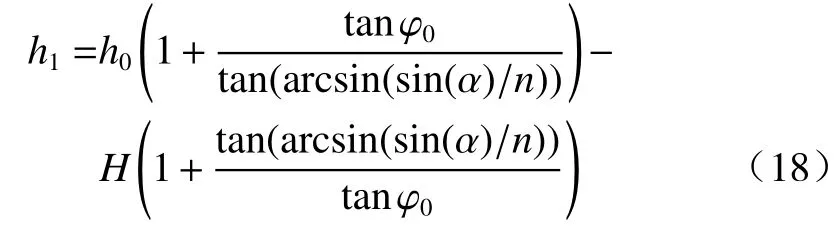
则不同高度处入射的光线在图像接收装置上的高度hc为

式中：L表示锥形透镜的锥长，由此可以求出在子午面处入射的光线照射到图像接收装置上的位置。

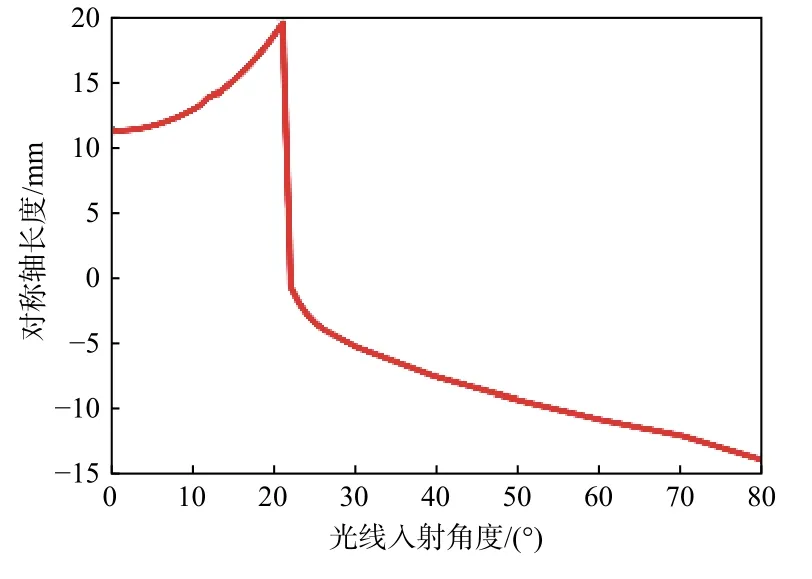
图3 子午面光线入射角度与出射光斑长度关系图Fig.3 Relationship between incident angle of meridian plane and length of outgoing spot

假设光阑放置在锥形透镜的大端端面处，锥形透镜的参数：材料折射率为1.72，其大端口径为10mm，锥角为28.1°。图3是子午面上的光线入射角度与出射光斑长度关系图（其中为负数的长度表示光斑位置在锥形透镜与图像传感器接触点的下方），这在一定程度上可以反应图像的面积变化情况以及不同全反射次数光线对应的图像位置。

2 测量装置系统仿真

根据前文分析，我们对该系统进行仿真分析。为得到较为合适的图像，我们选用折射率为1.72的锥形透镜材料，大端口径为10mm，锥角为28.1°，光阑放置在锥形透镜的大端端面处，大小与锥形透镜的大端端面口径相等，图像接收装置的面积为50mm×50mm。图4给出光线以不同入射角进入锥形透镜后得到的仿真图像，入射角从0°至80°。

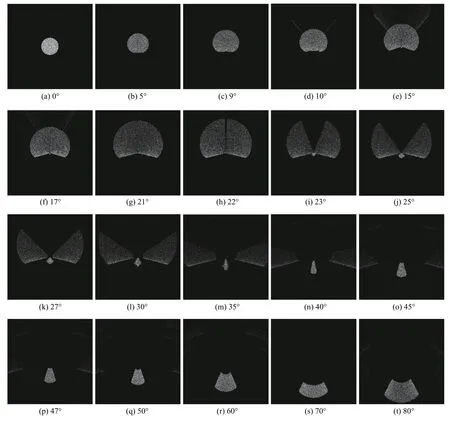
图4 不同角度入射光线形成的光斑仿真图Fig.4 Simulated light spot images of rays at different incident angles

由图中可以看出，不同入射角度的待测光线入射锥形透镜后具有不同的图像特征。根据仿真图像中光斑的块数可以看出，图4（a）～图4（g）所示光斑图像仅有一块，图4（n）～图4（r）可提取一个主要扇形亮块，图4（h）～图4（m）所示光斑图像主要有2个扇形亮块。根据图像边界夹角可分为上边界夹角、下边界夹角以及扇形夹角，图4（e）～图4（g）所示为仅有下边界夹角，图4（h）～图4（o）所示为有上、下边界夹角，图4（n）～图4（t）所示为有扇形夹角和亮块。根据图像的矩特征，图4中所有光斑图像可提取零阶矩（面积）、一阶矩（重心）和二阶矩（转动惯量）等图像信息。

对于不同入射角度的光线，可根据其图像特征信息不同划分为几类。如表1所示，将光线入射角度划分为4类，其中第1类为光线入射角度在0°～10°范围内，整体光斑图像仅有1块；第2类为光线入射角度在10°～21°范围内，整体光斑图像仅有1块，且图像特征包括图像下分裂为具有一定角度的扇形；第3类为光线入射角度在21°～40°范围内，整体光斑图像分裂为2块，且图像特征包括图像上分裂角度、下分裂角度；第4类为光线入射角度在40°～80°范围内，容易提取到1块明亮扇形光斑图像，图像特征包括图像扇形区域和角度。

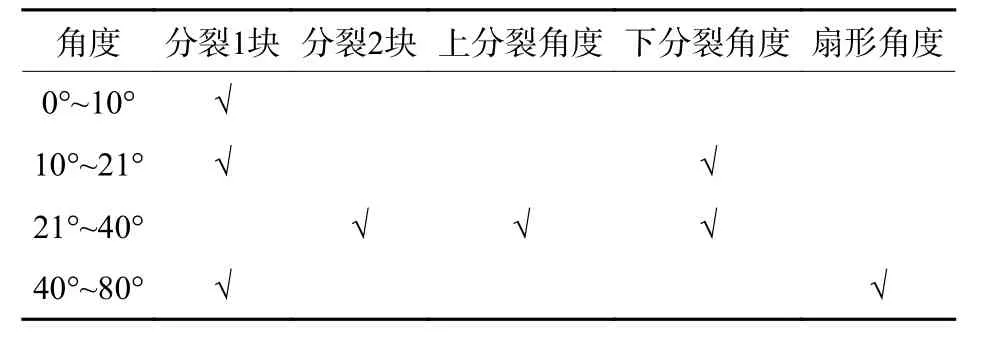
表1 不同入射角度的光线具有的图像特征Table1 Image characteristics of light rays with different incident angles

3 仿真结果分析

图5为光线入射角度测量模型，其中 β为光线入射的方位角，δ为光线入射的倾斜角。通过图像接收装置接收到的光斑图像具有轴对称性[10]，显而易见图像对称轴的方向确定了图5中光线的方位角β角度。我们采用主成分分析法求取图像对称轴角度[11]，根据卢春雨提出的基于主元分析的对称性检测方法[12]，若平面图像协方差矩阵的2个特征值不同，则图像对称轴的方向必为2个特征向量方向的子集，也即二维图像的2个特征向量方向中的1个必为图像对称轴方向。基于以上理论，我们可以通过求取图像协方差矩阵的特征向量方向来求取图像对称轴的方向。

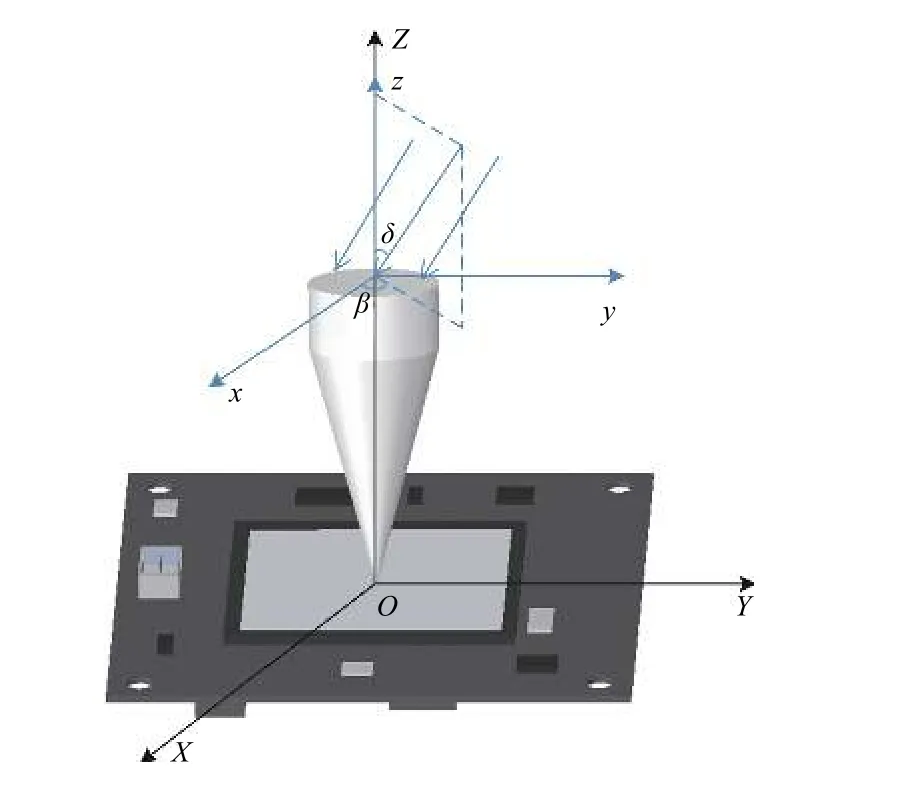
图5 光线入射角度测量模型Fig.5 Measurement model of light incident angle

基于以上理论，我们可以通过求取图像协方差矩阵的特征向量方向来求取图像对称轴的方向。对称轴检测的算法如下：

1）由图像出发，对图像进行中值滤波、最大类间方差法[13]二值化等操作；

2）求取图像质心；

3）计算图像协方差矩阵并进行特征值分解；

4）设定阈值检测2个特征值是否相等，对2个特征向量方向进行验证，确定图像对称轴。

如图6所示，该图为依据图4中的光斑仿真图像、采用主成分分析法求取的图像对称轴角度残差与光线入射方位角角度关系图，图4中图像的对称轴角度理论值为90°。从图6中可以看出，当光线入射角度在0°～13°范围内时，图像对称轴角度检测的残差值最大会超过±1°；当光线入射角度大于13°时，对称轴角度残差值在±1°以内；当光线入射角度大于25°时，对称轴角度残差值在±0.2°以内。

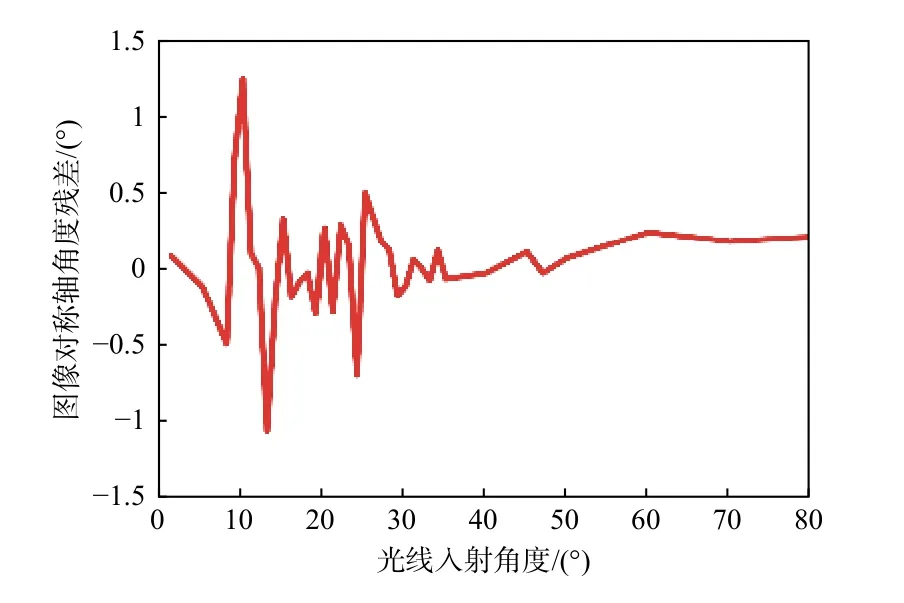
图6 图像对称轴角度残差与光线入射Fig.6 Relationship between residual angle of axis of symmetry and incident azimuth angle of light

在具体实现时，首先以锥形透镜锥尖与图像传感器接触点为坐标原点O，计算图像对称轴方向，这样就确定了图6中的方位角β角度。求出入射光线方位角后，将图像坐标系XOY通过坐标旋转转化到以光斑图像的对称轴为Y轴，以垂直对称轴的直线为X轴的世界坐标系XOY中，进而求取入射光线的倾斜角。

图像分布形式变化可以表达为1组图像特征，这组图像特征确定了图5中光线的倾斜角δ角度。其中，随光线入射角度的不同，会形成不同次数的光线全反射，所形成的图像特征变化具有分段单调特性。图4中仿真图的像素大小为698×698。图7（a）所示为图像面积与光线入射角度关系图，当光线入射角在40°～80°范围内时，可取光斑下部亮块的面积作为图像的面积。可以看出，在光线入射角度在0°～22°范围内，光斑图像的面积与光线入射角度呈一一对应关系；在光线入射角度在22°～40°范围内，光斑面积的单调特性不明显。在图4的仿真图中，以锥形透镜光轴与成像面接触点为坐标原点，图片水平向右方向为X轴正方向，图片竖直向上方向为Y轴正方向建立直角坐标系。图7（b）所示为该坐标系下光斑图像重心[14]坐标位置与光线入射角度关系图。从图中可以看出，当光线入射角度在0°～22°和大于22°时，重心位置分段单调特性较为明显。图7（c）所示为光斑图像转动惯量与光线入射角度关系，其中当光线入射角度大于40°时，用图像下部亮块来计算图像的转动惯量。转动惯量的计算公式为

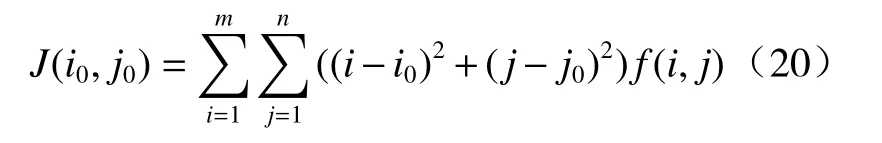
式中：(i0,j0)表示锥形透镜光轴与成像面交点；m、n表示图片的像素尺寸；f(i,j)表示在该位置处二值化图片的灰度值。由图7（c）中可以看出，当光线入射角度小于40°时，除光线入射角度为23°时图像的转动惯量有波动，其他角度处图像转动惯量单调特性明显；当光线的入射角度大于40°时，图像转动惯量单调。图7（d）所示为当光线入射角度在22°～40°范围内时光斑扇叶上部夹角[15-16]与光线入射角度关系图，从图中可以看出，在该角度区间范围内，光斑扇叶上部夹角的角度与光线入射角有一一对应关系，单调特性明显。

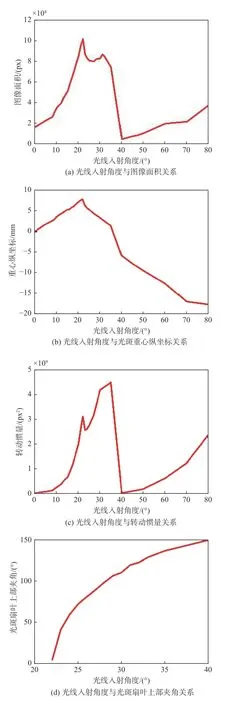
图7 光线入射角度与不同图像特征间的关系Fig.7 Relationship between incident angle and different image features

4 讨论

从上述分析可知，可以根据不同角度的光线入射到系统后形成的光斑图像的特征信息求取光线入射角度。具体方法为通过主成分分析法求取待测光线的方位角，通过光斑图像的特征信息求取待测光线的倾斜角。从图7可以看出，当光线入射角度在不同区间段内时，分别与一些图像特征成单调对应关系。表2和表3分别为当光线入射角度在不同区间段时采取的精测和粗测求解方案。当光线入射角度在0°～22°范围内时，光斑图像的面积与光线入射角度呈单调对应关系且角度越大，灵敏度越高；当光线入射角度在22°～40°范围内时，光斑图像扇叶上部夹角随光线入射角度的增大而增大且角度越大，灵敏度越低；当光线入射角在22°～24°范围内时，图像转动惯量有波动；而在24°～30°范围内时，图像转动惯量与光线入射角度呈单调关系；从图4中可以看出，当光线入射角在30°～40°范围内时，图像扇形面积有部分未显示，因此不对该区间内图像转动惯量予以讨论；当光线入射角在40°～80°范围内时，图像下部亮块的转动惯量和夹角分别与光线入射角度呈单调对应关系。通过表2和表3可知，采用图像转动惯量确定光线入射角度的方案，灵敏度更高，适合用作精测手段；采用图像面积和扇叶夹角确定光线入射角度的方案，灵敏度低，适合用作粗测手段。

表2 不同入射角度光线精测求解方案Table2 Methods of precise measurements of different ray incident angles

表3 不同入射角度光线粗测求解方案Table3 Methods of coarse measurements of different ray incident angles

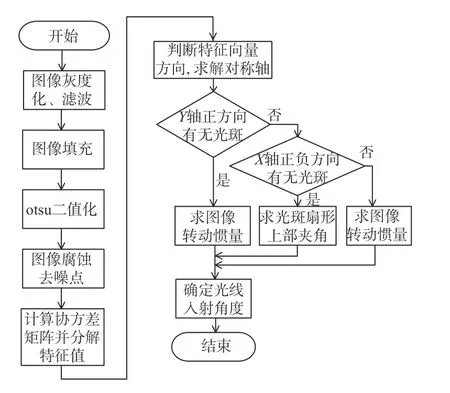
图8 光线角度计算流程图Fig.8 Flow chart for calculating the ray angle

针对不同入射角度的光线可以采取不同的求解方案，处理方案的流程图如图8所示。当光线入射角度在22°～40°范围内，光线在锥形透镜内增加了1次全反射使得光斑图像分裂且当光线角度大于35°后，有部分超出图像探测器，因此在22°～40°范围内采用转动惯量的测量方法光线角度单调性不够明显。

现在在该区间段内使用光斑扇形上部夹角作为测量方法，具体角度区间的判别依据为：以锥形透镜光轴与成像面接触点为坐标原点，以光斑图像对称轴方向为Y轴，垂直对称轴方向为X轴建立直角坐标系。可以看出，当光线入射角度在0°～22°范围内时，在坐标轴Y轴正方向始终有光斑图像分布；当光线入射角在22°～80°范围内时，在坐标轴Y轴正方向均没有光斑图像分布；当光线入射角度在22°～40°范围内时，在坐标轴X轴正负方向均有光斑图像分布；当光线入射角度在40°～80°范围内时，光斑图像下部亮块这一特征较为明显，亮块旁边的光斑分布图像可以通过图像处理算法滤除，因此在该角度范围内，X轴正负方向上没有光斑图像分布，具体如表4所示。根据坐标轴上有无光斑图像分布，即可确定光线入射角度范围。

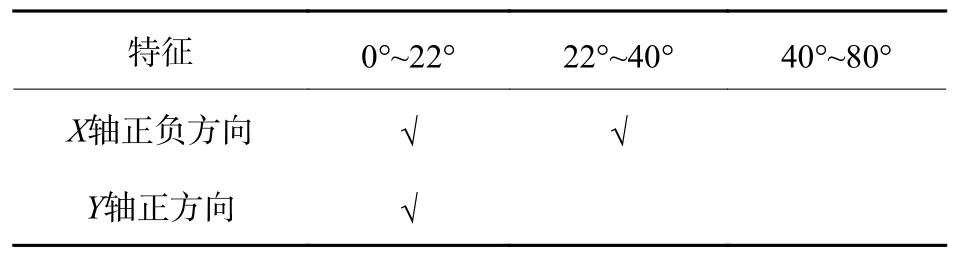
表4 不同入射角度光线图像分布情况Table4 Distribution of light images at different incident angles

与现有的角度测量传感器星敏感器[17]、太阳敏感器[18]对比，目前国内外星敏感器姿态测量精度可达到1″。采用本文锥形透镜测量法，测量范围在0°～22°（第一个分段范围）的视场角范围内，采用转动惯量的测量方法，精度可达1×10−4，因此精度比星敏感器要高3个数量级，视场角也比星敏感器大。

对比国内外高精度太阳敏感器，本文的精度比太阳敏感器要高，例如当采用转动惯量的测量方法时，精度可达1×10−4；当采用扇形上部夹角的测量方法时，测量精度优于其中∆x表示图像中一个像素所占的实际宽度，R代表图像中扇形上部夹角的边缘半径。所以，采用上述几种算法其测量精度都优于现有的太阳传感器，视场角相当。

由图3和图7（a）可以看出，光斑图像面积尺寸较大，因此图像接收装置应选用大尺寸CCD。一般来说，CCD 尺寸越大，像素数越多，感光效果越好，灵敏度就越高。本论文中求解方案的精度除了与光线的入射角度有关外，还与图像处理二值化算法中阈值的提取有关。如图6所示，在计算方位角时，采用最大类间方差法进行图像处理，除了在个别角度处计算出对称轴方向的残差大于1°，其他角度残差大致都在±0.5°范围内分布，在后续的图像处理方案中，可继续对二值化阈值提取方案进行改进，以获得更高的处理精度；也可以引入迭代算法进一步提升对称轴方向计算精度。同时在实际的应用中，可以通过标定技术减小各种测量误差，也可以通过双锥成像差分等方法提高测量精度。

5 结论

本文提出了一种基于锥形透镜的光线入射角度测量方案，通过理论分析和仿真实验论证了系统的可行性。仿真结果表明，不同入射角度的待测光线入射锥形透镜后所成的光斑图像具有不均匀性的轴对称结构，且具有不同的图像特征。由图像的对称轴方向可以确定待测光线的方位角；图像的特征如面积、转动惯量等与光线入射角呈分段单调关系，可高精度地测量光线的入射角度，并且具有大视场检测能力。