轨道交通混凝土箱梁低频噪声贡献源及空间分布

张天琦，周 力，罗雁云，吴 尚

（同济大学铁道与城市轨道交通研究院，上海201804）

随着轨道交通的快速发展，高架线作为一种节约土地资源、造价低于地下线的线路形式，在轨道交通领域内的应用不断增加［1］。箱梁振动产生的结构噪声主要为200 Hz 以下的低频噪声［2］，低频噪声具有衰减慢、传播距离远的特点，由此引发的高架线附近居民的身体健康和烦恼度问题日益突出［3-5］。

目前研究者大多采用有限元法［6-7］建立车辆-轨道-箱梁有限元模型，将轨道不平顺作为激励，模拟箱梁系统的动力响应。对于箱梁结构噪声辐射问题目前主要采用边界元法［8-10］，将仿真得到的箱梁结构竖向振动响应作为边界条件导入到边界元模型中，计算箱梁结构噪声；混合有限元-统计能量法［11］也常用来预测箱梁结构噪声。现有的轨道交通高架箱梁结构振动辐射噪声的仿真分析较少采用有限元法。原因在于：与边界元相比，有限元需要对空间和时间进行离散处理，网格密度较大、单元数目较多，导致计算速度较慢，但由于本研究对象为低频噪声，对网格密度的要求不高，因此可以采用有限元-无限元法。此外，现有研究对箱梁结构噪声的模拟很少进行各板件振动辐射噪声声压贡献的仿真以及从定量角度分析梁侧噪声的来源，而分析梁侧噪声的贡献源，有助于针对性地提出减振降噪措施。

基于30 m 双线混凝土简支箱梁振动和结构噪声现场实测，建立了车辆-轨道-箱梁有限元模型和箱梁振动-辐射噪声有限元-无限元模型。对列车运行条件下的箱梁各板件1～200 Hz 频带内的振动和辐射噪声进行仿真，对单个板件在行车侧25 m×13 m 声场内的噪声声压贡献进行计算，并分析了梁侧低频结构噪声的来源和空间分布特性。

1 车辆-轨道-箱梁耦合振动

1.1 车辆-轨道-箱梁有限元模型

1.1.1 基本假设

由于列车运行产生的振动是随机的，轮对引起的钢轨振动在轮对离开该点10 个扣件前后可以忽略，因此仅考虑一节列车作用下轨道、箱梁的动力响应。此外，考虑到钢轨边界对模型动力响应计算的影响，车轮与钢轨端部距离最小值不能低于30 m，建立的钢轨长度为90 m［12］。由于桥墩质量较大，列车荷载作用下的振动响应较小，因此产生的结构噪声可忽略不计。在建立有限元模型时不考虑桥墩，直接将梁体与地面连接［13］。

1.1.2 参数设置

车辆参数参照地铁B型车，钢轨为标准60轨；扣件采用弹簧-阻尼单元进行模拟，垂向刚度为5×107N·m-1、阻尼为1×104N·s·m-1。基于轮轨接触的基本理论，采用非线性赫兹接触模型计算轮轨法向接触力，切向摩擦和蠕滑行为则用摩擦系数法描述。选择美国六级谱作为模型的激励，采用三角级数法生成轨道高度不平顺值［14］，如图1所示，并将该值对应钢轨长度输入到模型中。

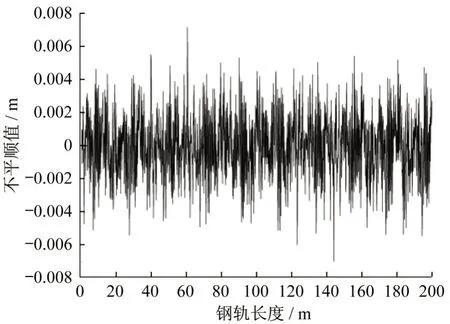
图1 轨道高低不平顺值Fig.1 High and low irregularity of track

箱梁为30 m跨度混凝土简支箱梁，采用三维实体模型，尺寸按照实际工况设置，如图2所示。箱梁弹性模量为3.5×104MPa，密度为2.5×103kg·m-3，泊松比为0.2。两端边界条件设置中仅约束纵向和横向位移，不约束垂向位移。利用离散的弹簧-阻尼单元模拟箱梁支座，仅考虑垂向刚度1.26×109N·m-1与阻尼2.04×105N·s·m-1。

图2 箱梁横截面（单位：mm）Fig.2 Cross section of box girder (unit:mm)

1.2 箱梁振动响应

某城市轨道交通30 m 跨度双线混凝土简支箱梁跨中横截面如图2所示。箱梁底板距地面9 m，桥上无声屏障，轨道结构为普通整体道床，采用WJ-2A扣件，运营车辆为6节编组B型车，通过平均速度为67.9 km·h-1。在顶板处布置振动加速度传感器，在底板、腹板和翼板处分别布置振动加速度传感器和传声器，如图2 中V1―V4 和N2―N4 所示。图3为根据实际工况采用有限元软件建立的仿真模型。

图3 车辆-轨道-箱梁有限元模型Fig.3 Finite element model of vehicle-track-box girder

表1和图4分别为实测和仿真得到的1～200 Hz内箱梁各部分振动加速度级和倍频程图。从图4可以得到以下结果：由于未考虑多节列车通过的附加作用，仿真结果略小于实测结果，但很好地模拟了各板件在1～200 Hz内的振级大小关系，均为底板＞顶板＞翼板＞腹板；仿真结果较好地体现了振动的频段特性，底板振动加速度级在40～63 Hz频段内出现全局峰值，在5～8 Hz、20～25 Hz频段附近出现局部峰值，在100 Hz左右存在局部振动；翼板振动加速度级在100 Hz左右出现最大值，在5～8 Hz、20～25 Hz和40～63 Hz频段内存在局部振动。这说明，对于箱梁振动仿真，所建立的车辆-轨道-箱梁有限元模型具有良好的精度。

表1 各板件振动加速度级仿真值和实测值Tab.1 Simulation and measurement values of vibration acceleration level of each plate

图4 各板件振动实测和仿真倍频程Fig.4 Vibration measurement and simulation octave of each plate

2 箱梁振动辐射噪声

2.1 箱梁振动辐射噪声有限元-无限元理论

声学无限元技术是一种基于半解析的方法。将声学主控方程在球形或椭球形坐标系下展开，通过级数叠加的形式来描述椭球面上的声学量，然后与有限元辐射边界匹配在一起，可以满足无反射边界条件［15］。在模拟无限流场时，采用声无限元技术来避免声波反射对计算结果的影响，该方法可根据不同需求减小有限元声场模型，降低建模和计算成本。

借助有限元软件模拟箱梁辐射的结构噪声，可避免由多软件交叉导致的文件在不同软件之间转化所带来的问题。考虑到本研究关注的频率上限为200 Hz，属于低频噪声，因而有限元网格密度不会太大。与边界元法相比，无限元法能够根据模型需求改变有限元声场的大小，从而降低建模和计算成本，并且两者计算结果相差不多［16］。

2.2 箱梁结构振动辐射噪声仿真模型

建立的箱梁结构振动辐射噪声有限元-无限元模型如图5所示。模型主要由三部分组成，即声-固耦合交界面（箱梁外轮廓）、无限边界（箱梁轮廓外的椭圆柱面，是箱梁结构振动辐射声场的外边界）、空气（两边界之间的填充）。所关注的频率上限fmax为200 Hz，因而网格尺寸L根据L≤c/(6fmax)（c 为声音在介质中的传播速度，取340 m·s-1）计算可得网格单元长度不大于0.28 m［17］。

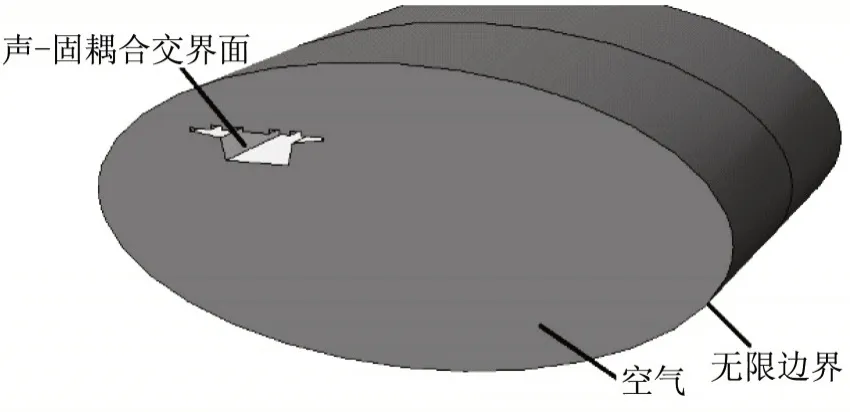
图5 箱梁结构振动辐射噪声仿真模型Fig.5 Simulation model of box girder structureborne vibration-radiation noise

将第1.2 节中仿真得到的箱梁振动输入到有限元-无限元模型中，可得到各板件近场（对应实测测点）噪声1～200 Hz 声压级和倍频程图，分别如表2和图6所示。可以看出，与实测对比，仿真得到的各板件附近噪声声压级大小规律与实测一致，均为底板＞腹板＞翼板，并且声压级的数量级一致；频谱特征基本相同，在50 Hz 左右出现全局幅值，在5～8 Hz、20～25 Hz 频段以及100 Hz 均存在局部峰值。由此可知，所建立的有限元-无限元模型可以很好地模拟板件振动辐射噪声。

2.3 箱梁各板件振动辐射噪声仿真模型

为得到箱梁各板件在梁侧的辐射噪声，以顶板为例，如图7 所示，将顶板处的交界面作为声-固耦合输入，而其他板件的外轮廓交界面设置为全反射，此时计算得到的辐射声场即为顶板的辐射噪声。其他板件的辐射噪声计算方法与之类似。

表2 各板件附近噪声声压级仿真值和实测值Tab.2 Simulation and measurement values of noise pressure level of each plate

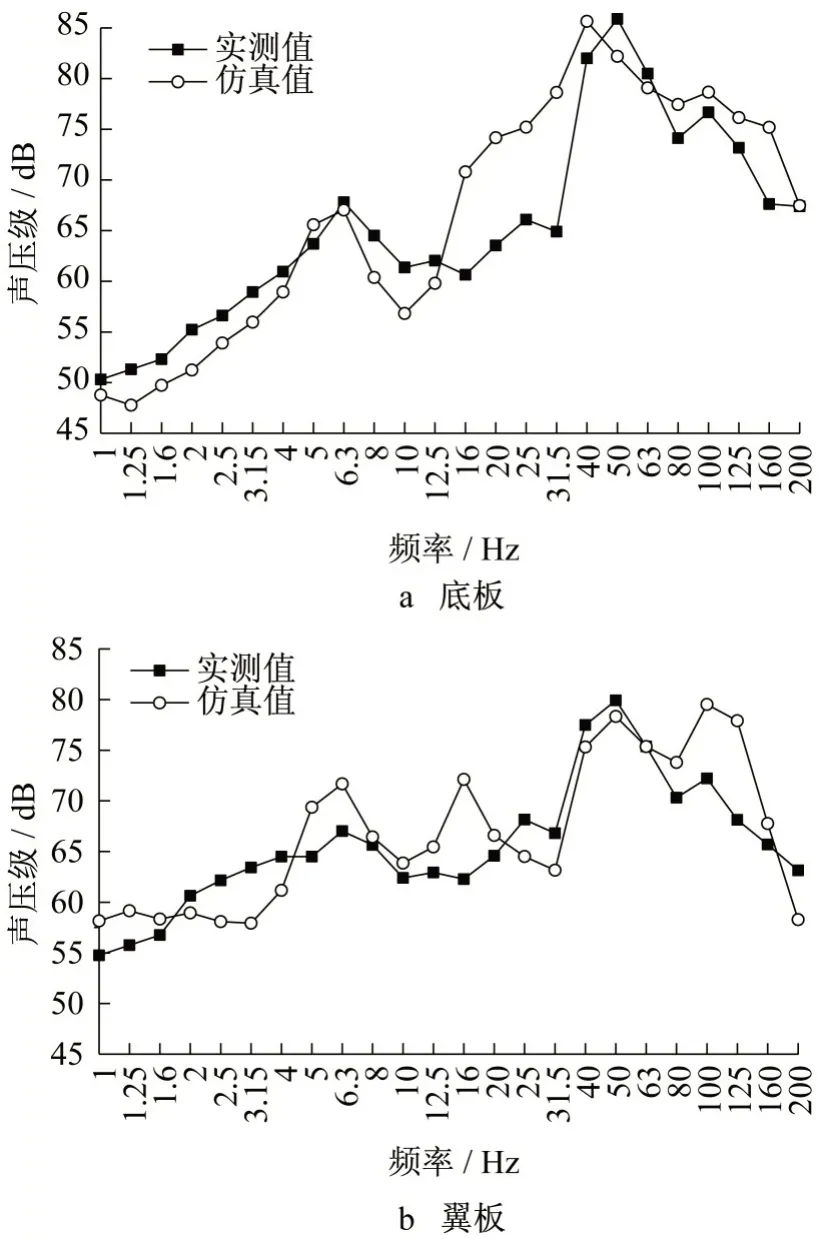
图6 各板件附近噪声实测和仿真倍频程Fig.6 Near-field noise measurement and simulation octave of each plate

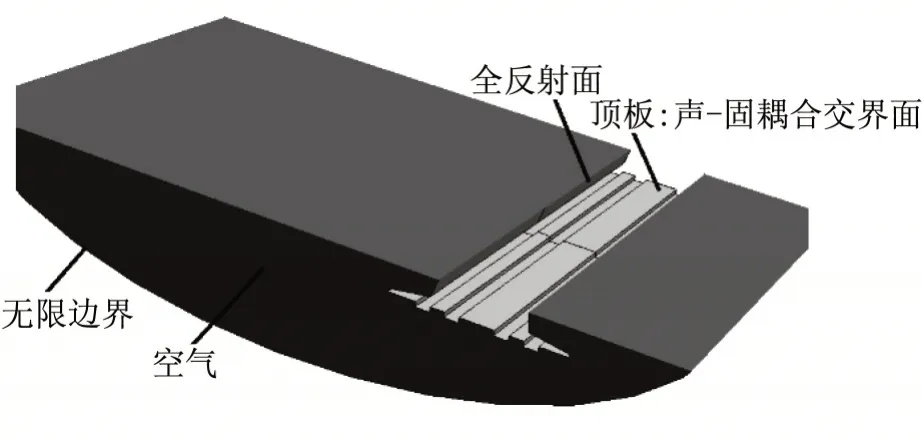
图7 板件辐射噪声模型（以顶板为例）Fig.7 Plate radiation noise model (taking top plate as an example)

图8 为计算得到的顶板振动在各板件附近（距各板件中心0.05 m）的辐射噪声频谱。可以看出，顶板处的结构噪声在各频率处明显大于在其他板件处的噪声，由此证明采用此方法可以计算得到单个板件振动辐射噪声。

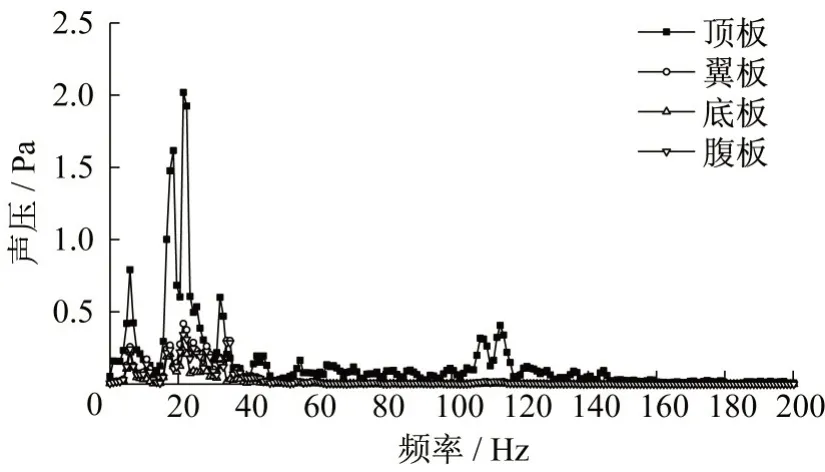
图8 顶板振动在箱梁各板件处的辐射噪声频谱Fig.8 Radiation noise spectrum of top plate vibration at each plate of box girder

2.4 板件声压贡献

混凝土箱梁可以看成由多块矩形板件组成，对于箱梁附近的场点，可求得箱梁在场点处的总声压p。为计算各板件的振动对场点总声压贡献，采用声学贡献系数Dc［11，18］，计算式如下所示：

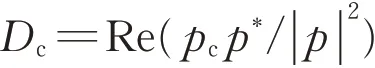
式中：p*为p的共轭复数；pc为构件在场点的声压；Re指取实部。

3 梁侧低频噪声源分析

为了分析梁侧低频结构噪声的主要来源，从而有针对性地提出降噪措施，在箱梁跨中截面呈网格状布置59个场点，共6列10行，如图9所示。行B与轨面平齐；行C与腹板中心平行；行D平行于底板噪声测点，与底板垂向距离为0.05 m；行J 位于地面，与底板垂直距离为9 m；其余行均为1.5 m等间距布置；列I 位于箱梁中心线处，以5 m 为间距向列车运行一侧布置5列场点。

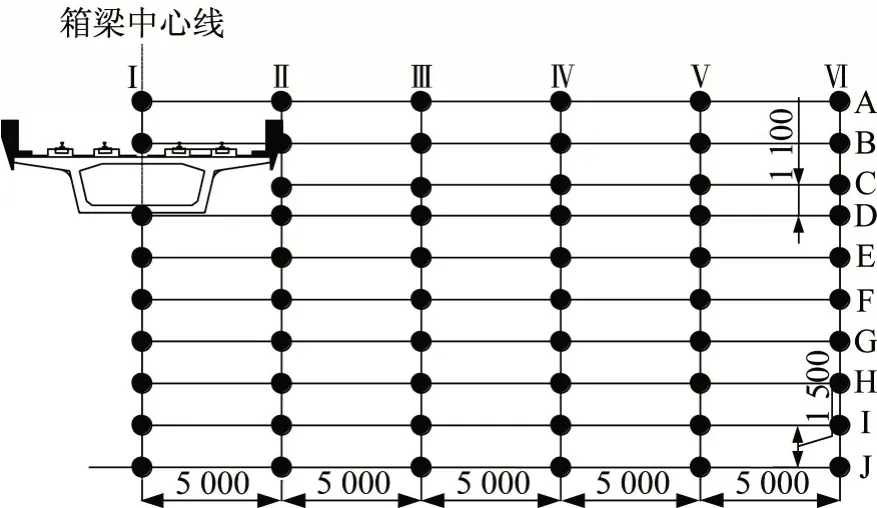
图9 梁侧场点位置（单位：mm）Fig.9 Location of the field on beam side (unit:mm)

3.1 声压贡献云图

箱梁各板块在梁侧的声压贡献云图如图10 所示。对每个板件振动在梁侧25 m 范围内产生的噪声（1～200 Hz）进行分析，得到以下结论：

（1）由图10a可知，底板对箱梁正下方区域影响最大，声压贡献最大可达100%。此外，底板振动对结构噪声的主要控制区域在底板下方空间约30°的范围内，如图10a中虚线所示，在此空间内底板对场点噪声的声压贡献大于50%。以虚线为界，底板的声压贡献在斜上方场点区域逐渐减小，直至顶板附近，声压贡献可几乎忽略不计，而且底板对近地面场点的声压贡献大于近箱梁场点的声压贡献。

（2）腹板振动对梁侧空间内声场的主要影响区域是一条从腹板开始斜向下约40°的窄带（如图10b中点划线所在区域所示），声压贡献约为18%；腹板声压贡献以该窄带为对称轴，向两侧区域递减。在窄带上方区域，声压贡献减小的幅度较小；反之在窄带下方区域，声压贡献减小得较快。在梁底板正下方，可以忽略腹板的影响。

（3）由图10c 可以看出，在顶板上方的区域，声压贡献大于100%，可见顶板对此区域的场点声压起主要作用，并且顶板辐射声压超过整体辐射声压，说明板件振动辐射的噪声在传递至该区域的过程中，发生了干涉现象；在顶板边缘的斜上方区域，顶板的声压贡献大于50%，说明在此区域声场也是顶板振动的主要作用范围，主要原因为声的绕射。从图10c中50%等值线开始（约为20°倾角），顶板的声压贡献沿顺时针方向快速降低，在底板正下方区域声压贡献减为零。

（4）翼板在梁侧声场的主要影响范围为以翼板为切线的圆形区域，如图10d所示，在这一范围内翼板的声压贡献为50%～70%；在此区域外，以该圆形区域为中心，翼板的影响逐渐减小，在顶板上方和声场右上方区域声压贡献减为零；同时，在圆形区域下方，在图10d 中点划线方向（近似垂直于地面）翼板的声压贡献变化较小，仅从50%降低至40%左右。

此外，箱梁各板件在不同频率下声压贡献可能有所不同，因此有必要对此进行分析。从第2.2节的仿真和实测结果可知，各板件振动辐射噪声的峰值基本在40～50 Hz频段内，在100 Hz处出现了较大的局部峰值，因此分析箱梁各板件在40～50 Hz频段内和100 Hz处的梁侧声场声压贡献，如图11和图12所示。

综合图10 和图11、图12 可以看出：除了个别区域由于发生了声波的干涉导致局部声压分布规律发生变化外，各板件在峰值40～50 Hz 频段内、峰值100 Hz 处与1～200 Hz 频段内的梁侧声场声压贡献分布规律基本一致。

在3 个频段内，底板对梁侧声场的最大声压贡献均达到了90%以上；在40～50 Hz频段内，距箱梁中心线20 m的近地面处出现了声波干涉；在100 Hz处，底板振动产生的结构噪声在距箱梁中心线25 m的近地面以及距地面9 m处出现了声波干涉。

对于腹板振动而言，在40～50 Hz 频段内、100 Hz 处的声压贡献最大值分别大于25%和180%，大于在1～200 Hz 频段内的最大声压贡献；在40～50 Hz频段内，声波干涉出现在了距箱梁中心线20 m的近地面处；在100 Hz处，距箱梁中心线20 m、距地面3 m和9 m处出现了声波干涉。

顶板振动在2个峰值频率处的声压贡献最大值（250%）同样大于在1～200 Hz 频段内（140%）；在2个峰值频率处，声波干涉均出现在了距箱梁中心线25 m、距地面11 m处。

翼板振动在40～50 Hz 频段内的声压贡献云图与在1～200 Hz频段内的基本一致，并且声压贡献的最大值均在70%以上；在100 Hz 处，声波干涉出现在了距箱梁中心线5 m、20 m 的近地面处以及距箱梁中心线20 m、距地面9 m处，并且声压贡献的最大值大于80%。

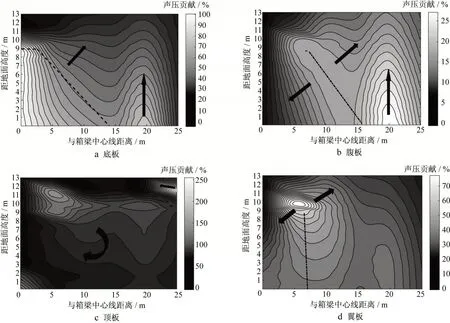
图11 40～50 Hz频段内各板件声压贡献云图Fig.11 Sound pressure contribution coutour of each plate from 40 Hz to 50 Hz

3.2 各板件辐射声场的空间分布特性

在4个板件中，腹板声压贡献最小，在考虑降噪措施时可以不予重点考虑，并且按照箱梁各板件在1～200 Hz频段内的声压贡献大小关系，箱梁一侧基本可以分为3个区域，如图13所示。

（1）在底板正下方及斜下方30°区域内（区域1），底板振动对场点噪声起主要作用，并且各个板件的声压贡献大小顺序为底板＞翼板＞腹板＞顶板。

（2）在轨面正上方（区域2-1）及腹板斜上方20°区域（区域2-2），顶板振动对场点声压贡献最大（均大于50%，并且在箱梁正上方154°范围内（区域2-1）大于100%），其次为翼板（约为20%～40%）、腹板（约为10%～20%），底板最小，可忽略不计。

（3）在上述2个区域以外的空间范围（区域3）内，底板和翼板振动声压贡献基本相当（约为20%～50%），大于腹板（约为20%），顶板最小（小于20%）。

综合图10和图13分析可得：

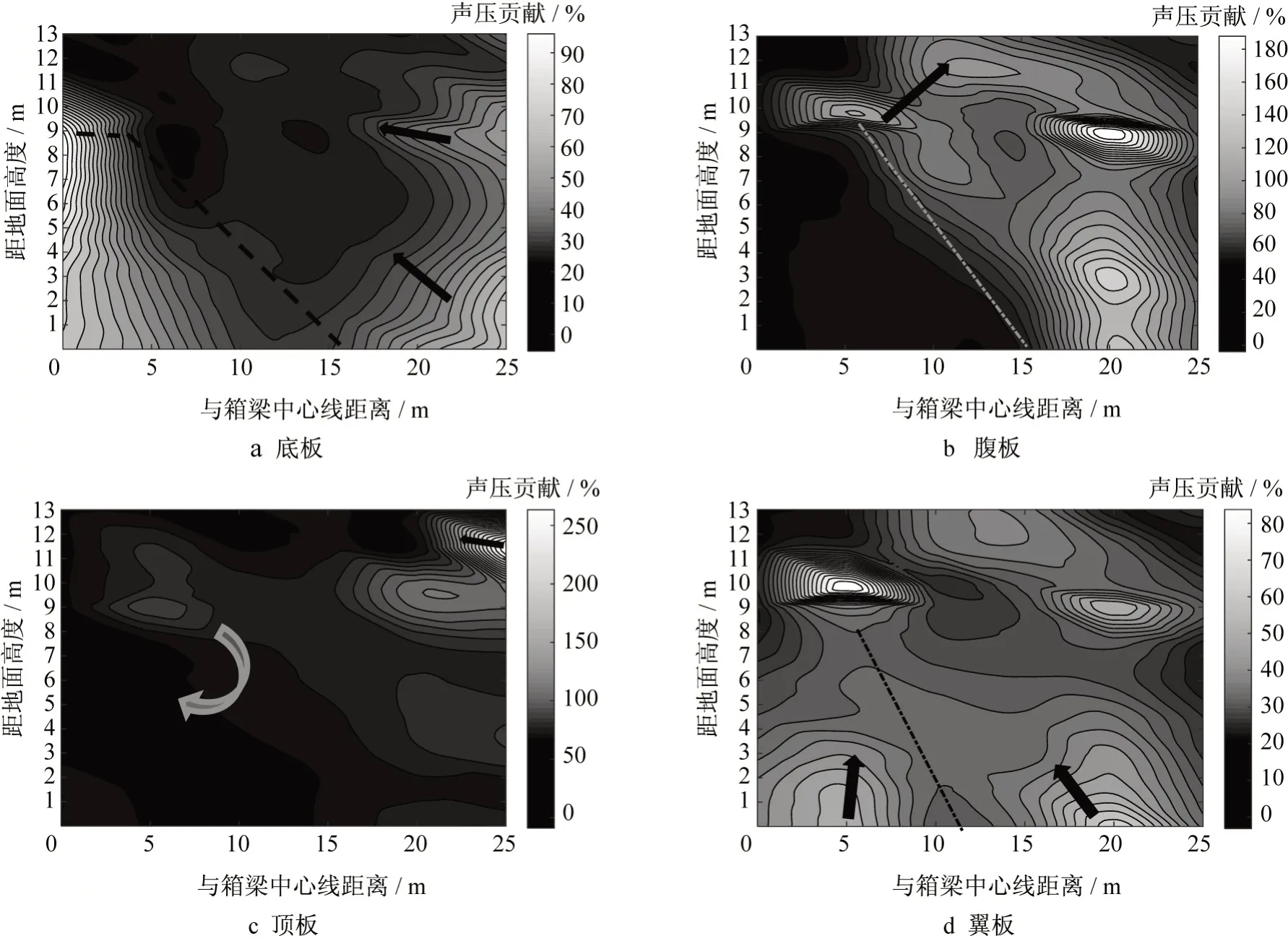
图12 100 Hz处各板件声压贡献云图Fig.12 Sound pressure contribution coutour of each plate at 100 Hz

图13 声场区域划分（单位：m）Fig.13 Sound field division(unit:m)

（1）从与箱梁中心线距离的角度来看，近场声压主要受底板振动的影响，其次翼板，略大于顶板和腹板；远场噪声主要由底板和顶板的振动决定，大于翼板，腹板最小。

（2）从距地面高度的角度来看，近地面区域（距地面0～4 m）噪声各板件声压贡献大小顺序为：底板远大于翼板，腹板次之，顶板最小。对于箱梁附近声场（箱梁底面以下范围），板件声压贡献大小顺序为底板＞翼板＞顶板＞腹板。箱梁顶板以下、底板以上区域内，顶板声压贡献略大于翼板，两者起主要作用，而底板和腹板声压贡献基本在10%～20%；对于顶板以上声场，顶板声压贡献基本在50%以上，顶板正上方声压贡献甚至大于100%，远大于其他各板件。

板的法向振动和声辐射效率是决定辐射噪声的主要因素，从第1.2节的仿真和实测分析中可知，底板振动最大，并且由于底板面积大于腹板和翼板，振动辐射的噪声较大，因此底板振动在底板以下区域起主要作用。顶板的法向振动略小于底板，面积大于底板，但由于箱梁本身的遮蔽作用，顶板振动辐射的噪声难以绕射至底板附近及下方区域。腹板的法向振动小于其他板件，因此对场点声压的影响并不明显。

4 结论

（1）采用有限元-无限元相结合的方法计算箱梁结构噪声具有良好的精度，而且采用同一有限元软件可以避免多软件交叉所带来的问题。

（2）在1～200 Hz频段内，腹板对整个声场的声压贡献均小于20%，在4个板件中，腹板声压贡献最小。底板正下方及斜下方30°声场内为底板结构噪声的主要影响区域，声压贡献达到50%～100%。在顶板正上方及斜上方20°声场内，顶板起主要控制作用，声压贡献均在50%以上。在前述两区域外，底板和翼板是结构噪声的主要来源，两者的声压贡献之和达到60%～80%。

（3）在辐射噪声的峰值频段40～50 Hz 及局部峰值频率100 Hz 处，各板件在梁侧声场的声压贡献分布规律与在1～200 Hz频段基本一致，区别为在距箱梁中心线20～30 m的近地面处以及距地面9 m处发生了声波干涉。

（4）在1～200 Hz频段内，近场声压主要受底板的影响（50%以上），其次是翼板，略大于顶板和腹板。各板件的辐射噪声在远场场点声压贡献大小顺序为：底板和顶板大于翼板，略大于腹板。对于近地面场点，各板件声压贡献大小顺序为：底板≫翼板＞腹板＞顶板。近箱梁场点（底板以下），声压贡献大小顺序为底板＞翼板＞顶板＞腹板。箱梁同一高度，顶板声压贡献略大于翼板，两者起主要作用，而底板和腹板的声压贡献几乎可以忽略。顶板以上空间，顶板起主要作用，并且声压远大于其他板件。