磁流变抛光回转对称非球面工件精确自定位

周 涛，张云飞，樊 炜，黄 文，张建飞

(中国工程物理研究院 机械制造工艺研究所，四川 绵阳 621900)

1 引 言

在光学系统中使用非球面光学元件，可有效地消除球差、彗差、像散、场曲，减少光能损失，从而获得高质量的图像效果和高品质的光学性能[1-4]。磁流变抛光技术具有去除函数稳定、去除效率高及面形收敛性好等优点，在非球面光学工件抛光中应用广泛[5]。利用磁流变抛光技术对光学工件进行高精密抛光，需对工件进行精确定位。传统定位方式利用千分表及工装对工件进行手动调平及找正，在调平、找正的基础上利用测量系统[6]测量工件位置信息，以建立准确的工件坐标系。当被加工件尺寸较大或被加工表面为非球面时，人工精确调平效率非常低，且当对工件进行多次迭代加工时，每次加工都需要重新手动调节工件姿态，加工精度和效率会受到影响。因此，实现非球面工件的位姿求解，解决磁流变抛光中的自定位关键问题，对提高磁流变抛光工件定位效率，提高磁流变抛光设备的智能化水平有着重要的意义。

工件自定位指利用计算机及传感器测量系统，通过位姿求解算法实现工件实际工况下的精确定位，其本质是三维点云的精确配准[7-8]。近年来，国内外研究者围绕三维点云匹配问题展开了系统的研究[9-13]。其中，最具代表性的是由Besl和McKay提出的迭代最近点算法[12](Iterative Closest Point， ICP)，该算法实现简单、精度高，但对初始迭代矩阵的要求非常严格，且由于迭代计算过程中需反复求解匹配对应点，算法计算量很大。为此，许多研究者对算法进行了改进。Rusinkiewicz等[14]提出法向均布采样法，有效改善了迭代收敛速度，但方法鲁棒性未得到验证。徐金亭等[15]为解决曲面匹配的初值敏感性问题，提出了基于曲面曲率特征的初始矩阵建立方法，并通过仿真验证。刘胜兰等[16]为解决零件表面精度差异性对模型配准精度的影响，提出先利用高精度特征配准约束部分配准方向，再用低精度特征完成整体配准的方法，并通过叶轮定位配准验证。张洪帆等[17]为解决飞机蒙皮加工过程中的精确定位问题提出基于ICP算法的两级定位策略，通过粗、精定位方法，实现了飞机蒙皮件的精确定位。李文龙等[18]为解决复杂曲面零件三维配准中固有测量缺陷对匹配精度的影响，提出基于方差最小化原理的匹配方法。文献[15-18]所述方法主要聚焦于解决传统机械加工中复杂曲面的无约束匹配问题，匹配结果具有唯一性。在无约束情况下，回转对称工件的匹配结果具有非唯一性，因此上述方法均无法应用于具有回转对称特性的光学工件。为解决圆柱形平面光学工件的定位问题，王彦哲等[19]将基于经典ICP算法的工件自定位方法应用到磁流变抛光定位中，通过人工标记点对匹配剩余自由度进行了约束，并进行了抛光验证实验，但通过在平面上添加标记点的方法，需通过手动方式对标记点进行测量，测量的自动化水平不高，且测量精度及定位精度受人工经验影响。

本文针对磁流变抛光回转对称非球面工件的精确自定位问题，根据磁流变抛光工件的定位要求，确定了磁流变抛光工件精确自定位原理，分析了经典ICP定位算法直接应用于回转对称非球面工件精确定位时存在的问题，提出了通过构建特定迭代初始矩阵实现指定性匹配的方法与提高匹配效率的空间映射方法，并以此为基础提出了改进后的两级ICP定位方法(Improved Two-Level Iterative Closest Point，ITLICP)。实验证明，本文提出的ITLICP磁流变抛光工件定位方法，在保证定位精度的同时，极大地减少了加工辅助时间，提高了磁流变抛光回转对称非球面工件的定位效率。

2 磁流变抛光工件定位需求及原理

2.1 定位要求

磁流变抛光示意图如图1所示，磁流变液在抛光轮带动下循环流动，在磁场作用下磁流变液变成Bingham介质并在工件表面与之接触的区域产生剪切力，实现材料去除[20]。磁流变液未与工件接触时，在磁场作用下于抛光轮底部形成厚度为H的凸起；与工件表面接触后，缎带凸起被挤压，挤压距离称为浸入深度[21]。浸入深度的变化会引起去除函数的变化，为实现磁流变高精度抛光，需对浸入深度进行严格控制，保持浸入深度恒定。由图1可知，记抛光轮最低点OPW与工件表面抛光点O的距离为h，则浸入深度可表示为：

Δh=H-h.

(1)

文献[19]中提出，为满足光学元件的加工需求，缎带浸入深度的误差需控制在±10 μm内。抛光缎带的稳定性控制与工件定位无相关性，本文不进行研究，H视为常量，则浸入深度的控制精度取决于h。因此，在抛光过程中需要根据光学元件抛光点的实际Z向位置对抛光轮进行控制，且Z向定位误差需控制在±10 μm内。

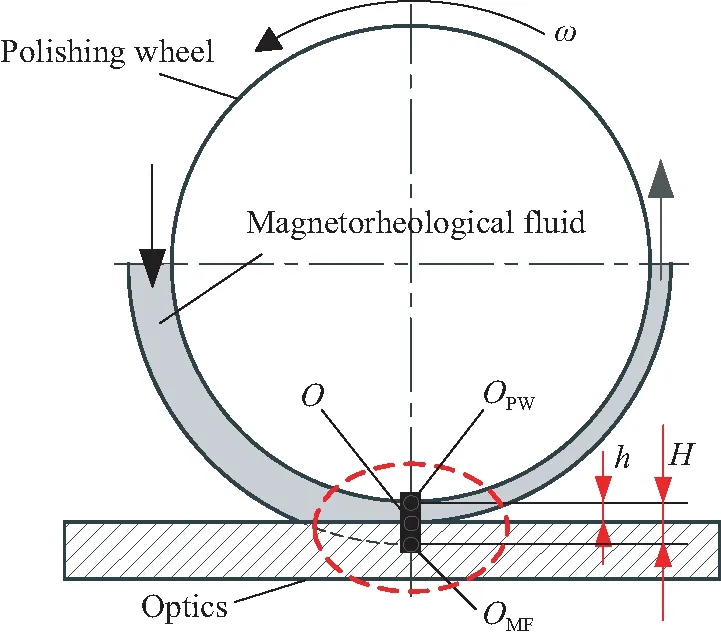
图1 磁流变抛光示意图Fig.1 Schematic diagram of magnetorheological polishing

2.2 定位原理

磁流变抛光中工件位姿精确定位由对刀工艺实现。基本对刀工艺过程包括调平、找正和位姿测量。利用高精密位移传感器，对调平及找正后的工件位姿进行在位测量，计算工件几何特征点坐标，并以此为坐标原点建立工件坐标系。对于回转对称非球面工件，通常以加工面回转对称中心线交点(顶点)为特征点。如图2所示，以凹抛物面为例，所测加工面顶点为工件坐标系原点，建立了与机床坐标系O-XYZ平行的工件坐标系Os-XsYsZs。进行磁流变抛光工艺规划时，为便于非球面各点位置的解析计算，通常会根据工件形状特征建立理想姿态下的工艺坐标系，且抛光过程中，将上述对刀过程所建立的工件坐标系与工艺坐标系视为重合。因此，找正与调平能够保证工件位姿与理想位姿一致。

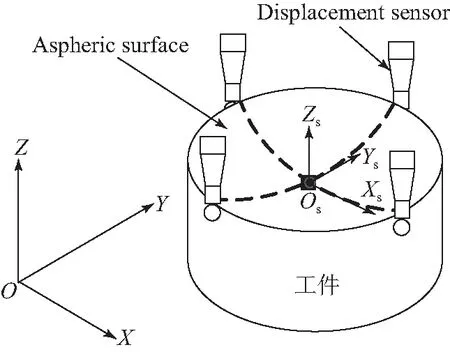
图2 磁流变抛光中工件坐标系Fig.2 Workpiece coordinates in magnetorheological polishing

未进行工件找正及调平时，工件实际位姿与理想位姿存在偏差。由刚体变换理论[23]可知，在相同的机床坐标系下，工件理想位姿可由实际位姿进行刚体变换得到。对工件表面任意点，假设理想位姿下机床坐标为(xid，yid，zid)，实际位姿下机床坐标为(xre，yxre，zxre)，则存在刚体变换矩阵Ttr，使：

(xid，yid，zid，1)=Ttr(xre，yxre，zxre，1)，

(2)

其中变换矩阵Ttr可表示为：

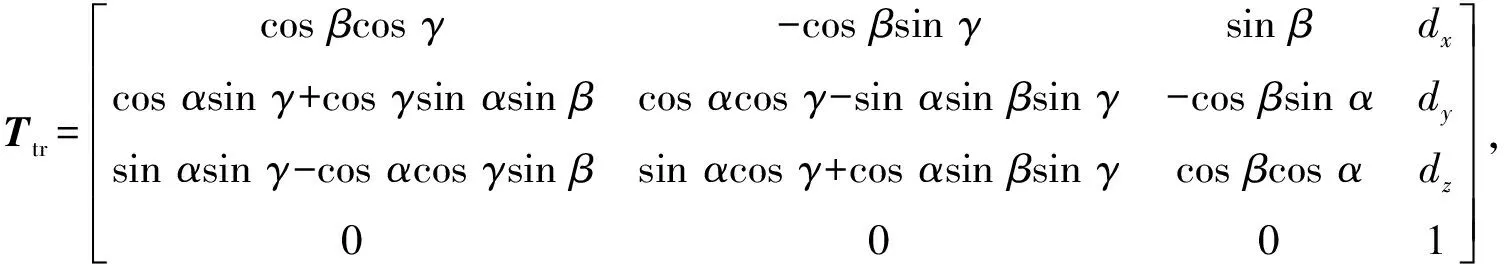
(3)

式中：α，β，γ为工件实际位姿绕机床直线轴X，Y，Z的旋转角；dx，dy，dz为工件实际位姿沿机床X，Y，Z轴的平移量。

因此，工件定位问题的本质是求解相同机床坐标系下工件实际位姿与理想位姿之间的刚体变换矩阵。在未找正及调平的状态下，为描述工件的实际位姿，利用高精密传感器对工件的实际位姿进行测量，测量点集记为点云M={mi|mi=(xi，yi，zi)T，i=1，…，Nm}。理想位姿则通过离散化工艺坐标系下工件的CAD理论模型来描述，记为P={Pi|Pi=(xi，yi，zi)T，i=1，…，NP}。由于测量点云M中所有点在理想位姿点云P中的对应点均未知，引入最小二乘的思想，将位姿求解问题描述为：已知测量点云M，CAD模型点云P，求解刚体变换矩阵Ttr及M的对应点，使得式(4)最小。

(4)

利用磁流变抛光技术进行修形的光学工件，其加工面的面形误差通常在几个波长内，几何精度非常高，而非加工面通常用于安装支撑，精度等级相对较低且不同工件之间具有较大的差异。为避免非加工面几何误差导致定位精度下降，且使定位方法更具通用性，本文中工件的实际位姿测量点均在加工面上。

3 回转对称工件定位

3.1 经典ICP点云匹配算法

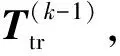
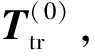
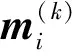
(5)

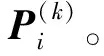
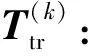
(6)

第4步：由式(7)计算匹配后两点云的平均匹配误差τ：

(7)

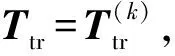
经典ICP算法具有精度高、实现简单及适应性好等优点，可实现任意形状点云的配准，但算法要求两组点云具有包含关系，且匹配结果受初始值影响较大，具有局部收敛特性。基于经典ICP算法的工件位姿匹配结果受初始变换矩阵及匹配过程中点对关系建立的影响，直接应用于回转对称非球面工件的位姿匹配，存在匹配结果不唯一和计算效率低的问题。

3.1.1 匹配结果不唯一

由于工件具有回转对称特性，工件表面的测点无法实现绕机床Z轴旋转角度γ的精确定位，理论上任意匹配结果绕机床Z轴旋转任意角度得到的变换矩阵，均能实现测量点云与理想点云的精确匹配，γ的匹配结果取决于初始旋转矩阵的设定。图3所示为同组目标点云与测量点云在不同迭代初始矩阵下得到的结果。

图3 不同初始旋转矩阵迭代匹配结果Fig.3 Iterative matching results caused by different initial rotation matrix

3.1.2 计算效率低

为满足CAD模型点云P与测量点云M之间的包含关系，且所有测量点在P中均能找到准确的匹配点，对CAD理论模型进行离散时，离散间隔应小于定位精度。磁流变抛光中工件的Z向定位误差需控制在±10 μm内，考虑到实际加工过程中存在机床运动误差，定位匹配误差需控制在在更小的范围内。以5 μm的间隔对直径为Φ100 mm的非球面工件进行离散化，点云P的规模为31 415.93万，经典ICP算法的时间复杂度为O(NmNp)，遍历搜索将耗费大量的时间。实际加工中，光学工件尺寸往往更大，经典ICP算法的计算效率较低。

3.2 回转对称非球面工件定位

3.2.1 局部收敛指定性匹配

针对匹配结果不唯一的问题，本文提出通过构建特定的初始迭代矩阵，实现Z轴旋转角度与设定值相同的匹配方法。初始迭代矩阵的构建包括确定初始旋转角α，β，γ及平移距离dx，dy，dz。

首先设定初始旋转角。手动找正、调平再对刀工件定位模式下，回转对称非球面工件的找正定位依靠工件侧面的定位线，本文采用相同方式使工件侧面定位线与X及Y轴分别平行，绕机床Z轴旋转角度γ设定为0。找正后，对工件进行目视初略调平。此时，α，β值较小，可近似为0。

然后设定初始平移距离。以机床坐标系为工件理想位姿CAD模型坐标系，两点云的平移量近似值通过五点法得到。如图4所示，在机床坐标系下，测量工件侧面4点的位置信息。1，3测点连线与Y轴平行，2，4测点连线与X轴平行。非球面工件曲面中心点坐标(xrc，yrc)为：

(8)

测量该点的Z向坐标值zrc，假设工艺坐标系下非球面工件曲面中心点坐标为(xc，yc，zc)，初始点云平移量为：

(9)

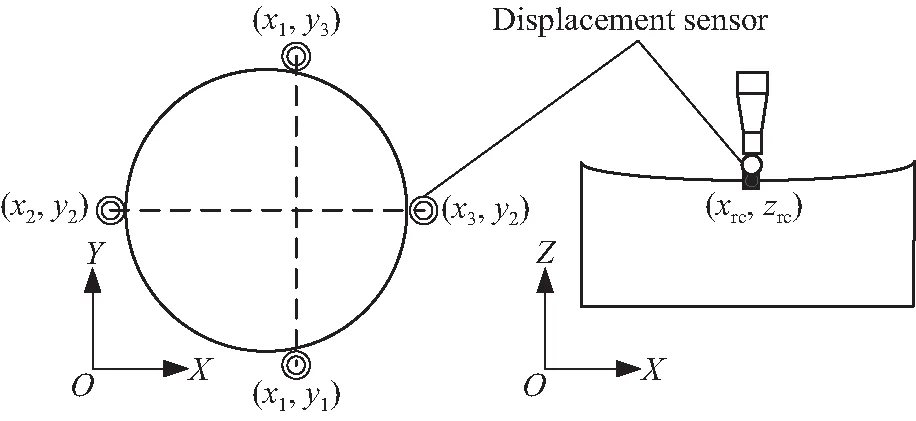
图4 五点法原理示意图Fig.4 Principle diagram of five-point measurement method

初始迭代矩阵可表达为：

(10)

3.2.2 两级ICP匹配改进方法

图5 空间垂直映射原理Fig.5 Principle of vertical mapping

对更新后的目标点云进行重新细化离散，并将一级匹配结果作为二级匹配的初始匹配条件，通过两级ICP匹配方式实现定位误差小于设定值的精确定位。结合前文所述的局部收敛指定性匹配，提出ITLICP，具体实现步骤如下：

(1)第一级ICP匹配

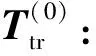
(11)

max{‖Ttr1·mi-Pi‖2，i=1，…，Nm}<Δw，

(12)

得到一级转换矩阵Ttr1。

(2)第二级ICP匹配

将测量点云M进行坐标变换，得到第一级匹配后的点云M1为：

M1=Ttr1·M.

(13)

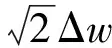
(14)

定位算法中，测量点数目Nm、第一级ICP匹配间隔Δw及第二级ICP匹配间隔Δw1是影响计算效率和定位精度的关键因素。

ICP算法要求测量点数目Nm不少于6个[12]，增加测量点数目可以减小偶然误差对定位精度的影响，但过多的测点数目会增加算法的时间复杂度，且耗费更多的测量时间，降低定位方法效率，因而测量点数目的选取需综合考虑传感器测量方式、测量精度、测量效率及定位效率。高精度机械接触式测量方法具有可靠性好及成本低的优点[6]，在工程中运用广泛，本文针对接触式测量方式，提出如图6所示的测量点分布策略。图6中，D表示工件直径，k为比例系数，当非球面工件边缘几何误差较大时，可设定相应的k将测点选取在几何精度高的区域。

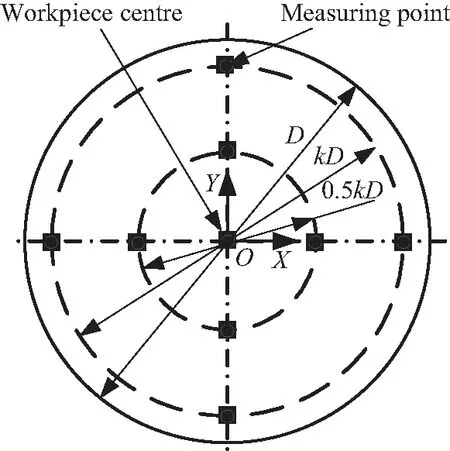
图6 测量点分布Fig.6 Distribution of measuring points

ICP算法的时间复杂度为O(Nm，Np)，测量点云点数相同，通过比较目标点云点数可实现ITLICP与经典ICP算法的效率对比。记回转对称工件的直径为D，则第一级ICP匹配目标点云数可表示为：

(15)

第二级ICP匹配目标点云数为：

(16)

为实现相同的定位精度，以Δw1为离散间隔直接对原始CAD模型进行离散，经典ICP算法定位求解的目标点云点数为：

(17)

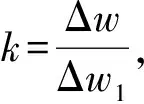
(18)

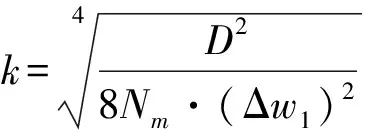
测点的实测位置精度不会超过机床运动轴的分辨率τ，为满足定位精度为δset的精确匹配，Δω1的取值为：

τ≤Δw1≤δset.

(19)

由于D的值远大于Δw1，因此在式(19)所示的取值范围内，Δw1对f(k)的影响较小，则Δw1的设定取决于它对定位精度的影响。由于Δw1取值越小，离散点云对理论CAD模型的描述越准确，定位精度也就越高，因此Δw1应设定为τ。

3.3 定位精度分析

两级定位方法ITLICP的精度主要受测点测量误差、非球面几何误差及工件找正误差的影响，这三种误差均会影响转换矩阵Ttr的计算结果。通过机床运动轴带动传感器对工件表面进行测量时，机床定位误差ε1及传感器误差ε2会导致测量误差，这两种误差均为随机误差，可以通过多次测量的方式提高测量精度。非球面几何误差为固有误差，可通过三坐标机、轮廓仪等高精密测量设备对工件非球面进行测量，并对CAD理论模型P进行修正。找正误差对绕Z轴的旋转角γ产生影响，本文采用的找正方式与传统方式相同，因而找正精度与传统方式相当，本文不展开讨论。

4 实验及结果

4.1 实验方案

(20)

定位误差中，Z向定位误差直接引起切深误差，X，Y向误差对切深误差的影响较小，因此本文设计实验对Z向定位精度进行验证。

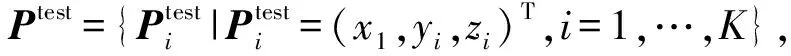
本文以一块Φ100 mm熔石英抛物面镜为实验对象，在自研六轴磁流变机床PKC-1000Q2上进行定位及验证实验，如图7所示。机床X，Y，Z的定位精度分别为6，6，3 μm，各轴运动分辨率均为1 μm。凹形抛物面镜的顶点曲率半径为480 mm，面形PV为0.22λ。位姿测量传感器为雷尼绍三坐标接触式传感器，重复定位精度为±1 μm。用于位姿求解的计算机配置为64位Win7操作系统、8 GB内存和i7-6700CPU。

图7 磁流变抛光回转对称工件及实验设备

Fig.7 Experimental workpiece and equipment for magnetorheological polishing of rotary symmetrical aspherical surface

4.2 实验结果与分析

为提高测量精度，定位实验中各测量点的测量结果为两次测量求取的平均值，验证实验中各测量点的测量结果均为10次测量求取的平均值。具体实验步骤如下：

步骤1：利用工件侧面定位线对工件进行精确找正及粗略调平，利用雷尼绍三坐标传感器进行5点测量，得到初始迭代矩阵为：

步骤2：按图6所示，取k=0.8，D=100 mm，测量实际工况下非球面工件表面9点坐标，得到工件实际位姿测量点云M，如表1所示。

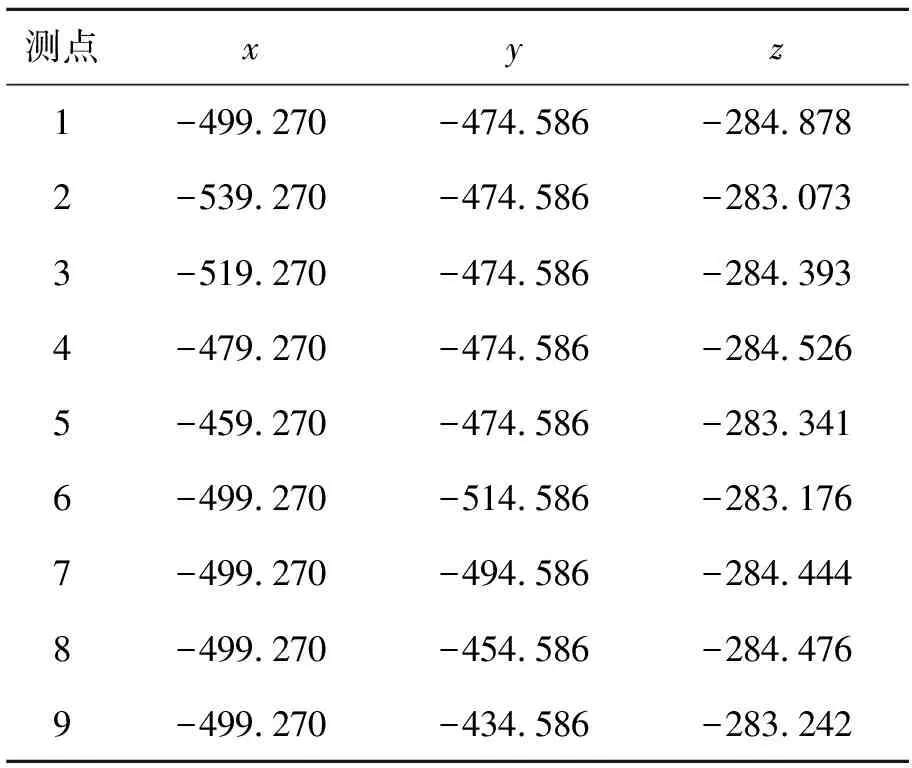
表1 工件位姿测量结果

步骤3：以抛物面顶点为坐标原点，对理想位姿下凹抛物面进行建模及离散，离散间隔为1 mm，离散点云P如图8所示。

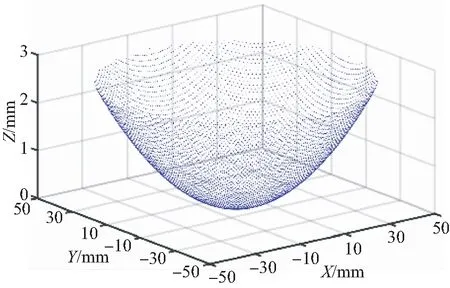
图8 CAD模型点云Fig.8 Point cloud of CAD model

步骤4：进行第一级ICP匹配计算，迭代求解得到一级转换矩阵。投影映射，以1 μm为间隔进行模型离散，对理想位姿点云进行更新，更新后点云P1如图9所示。将第一级转换矩阵作为第二级匹配初始迭代矩阵，令定位精度δset=7 μm，求解得到转换矩阵Ttr：

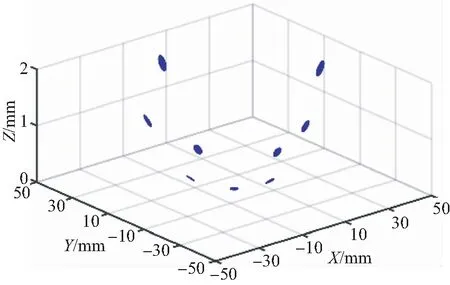
图9 映射后理想位姿点云Fig.9 Ideal point cloud after mapping

测量点云与理想位姿点云的两级ICP匹配结果如图10所示。求解式(21)所示非线性方程组，得到表2所示的刚体变换参数。

(21)

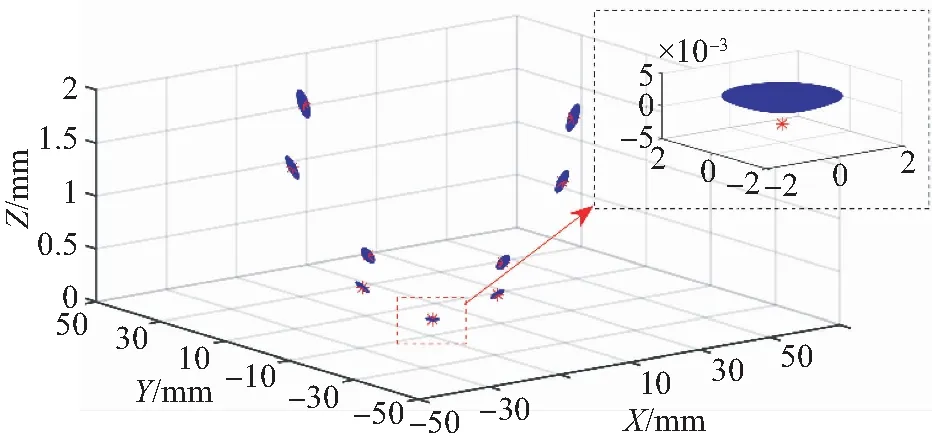
图10 点云匹配结果Fig.10 Matching result of point clouds

表2 刚体变换参数求解结果

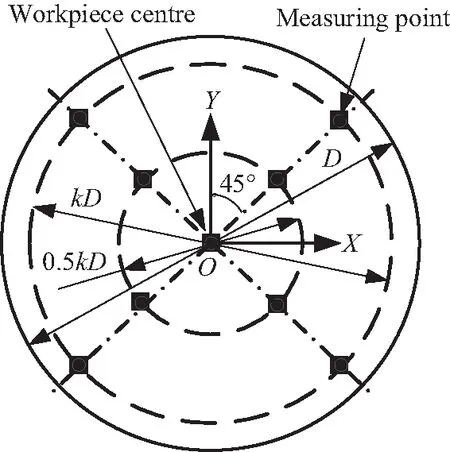
图11 测量点分布Fig.11 Distribution of measuring points

表3 验证点理想位姿

表4 验证点实际位姿测量结果

Tab.4 Measurement result of actual pose of verification points (mm)

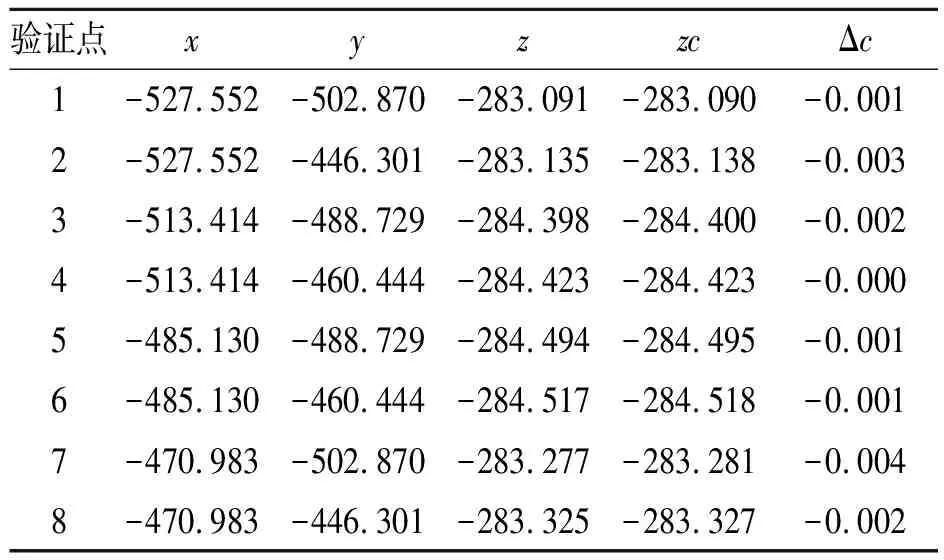
验证点xyzzcΔc1-527.552-502.870-283.091-283.090-0.0012-527.552-446.301-283.135-283.138-0.0033-513.414-488.729-284.398-284.400-0.0024-513.414-460.444-284.423-284.423-0.0005-485.130-488.729-284.494-284.495-0.0016-485.130-460.444-284.517-284.518-0.0017-470.983-502.870-283.277-283.281-0.0048-470.983-446.301-283.325-283.327-0.002

改变工件位姿，重复上述验证实验，图12所示为20次不同位姿下验证点Z向计算值与测量值的最大偏差Δzmax分布。Δzmax包含了测量误差及ITLICP定位误差。记测量点的实际值为zr，如式(22)所示：

zr=zc-ε1-ε2.

(22)

则ITLICP方法的定位误差ε可表示为：

ε=zr-zc=(zc-z)-(ε1+ε2).

(23)

由图12可知，实验中验证点Z向计算值与测量值的最大偏差为-5 μm，因此定位误差ε在(ε1+ε2)取最大正值时具有最大负值。多次测量求取均值后，验证点的实际定位误差ε1小于Z轴定位精度(3 μm)，且ε2≤1 μm，则在验证实验中，ITLICP方法的定位误差ε优于9 μm，满足定位要求。

图12 不同位姿下验证点Z向计算值与实测值的最大偏差

Fig.12 Maximum deviation between calculated value and measured value of verification pointZin different poses

为验证定位方法ITLICP在实际磁流变抛光中应用的可行性，对定位实验中Φ100 mm口径的熔石英抛物面镜进行磁流变修形抛光实验。首先，在非调平模式下对该抛物面镜进行位姿求解，然后对手动调平模式下按螺旋轨迹规划的NC代码进行修正，并进行抛光。图13所示为修形抛光前后的面形数据，工件面形误差PV值由0.22λ收敛到0.107λ，面形误差RMS值由0.033λ收敛到0.009λ，结果表明：定位方法ITLICP的定位精度满足磁流变抛光的定位要求，能够实现非球面抛光的有效收敛。传统方式下，完全依靠操作人员经验对Φ100 mm尺寸工件进行调平找正时，整个过程耗时约20～30 min。ITLICP定位方法在常规计算机上的平均计算时间为1.3 min，粗略调平及找正时间在3 min左右，测量点位姿的测量时间为3 min，共计7.3 min，大幅度减少了光学工件磁流变抛光时的定位辅助时间。

表5为ITLICP与经典ICP算法在相同收敛条件下的效率对比。在相同计算机配置下，经典ICP算法由于目标点云数据量过大，导致内存溢出，无法实现Φ100 mm工件在设定精度下的配准。ITLICP方法则能实现回转对称非球面工件绕机床Z轴回转角度设定为0的精确配准，定位精度优于9 μm，平均计算时间为1.3 min，极大地提高了计算效率。

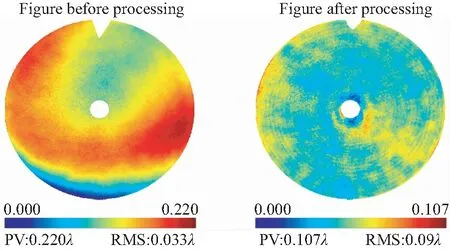
图13 抛物面镜自定位修形实验结果Fig.13 Experiment results of parabolic mirror modification after self-positioning

表5 ITLICP与经典ICP算法的匹配效率对比

5 结 论

本文根据磁流变抛光恒浸深控制要求，提出了一种基于ICP的回转对称非球面工件精确定位方法。实验结果表明：所提磁流变抛光定位方法ITLICP满足磁流变抛光的定位要求，可实现回转对称工件的有效收敛，多次实验中定位精度均优于9 μm，平均定位时间为7.3 min。与人工手动对刀相比，该方法在保证定位精度的同时提高了工件的定位效率。

定位方法中，关键参数会影响不同尺寸回转对称非球面的定位精度和效率，在以后的工作中，将继续完善相关参数的研究分析，以进一步提高定位方法的适用性。