孔数与孔厚对多孔板压损系数的影响机理

马有福，王凡，吕俊复

（1上海市动力工程多相流动与传热重点实验室（上海理工大学），上海200093；2热科学与动力工程教育部重点实验室（清华大学），北京100084）

多孔板作为管道内节流降压或流量测量元件，在减小管道振动、流动噪声及流动压损等方面较传统的单孔板具有明显优势[1-3]。由于影响多孔板压降特性的结构因素众多，对多孔板压降特性仍无清楚的机理性认识和可靠的压损系数预报方法，这制约了多孔板在实际工程中的应用。影响多孔板稳定区压损系数的结构因素主要有开孔等效直径比β、孔数n及孔板相对厚度t/d（t为孔厚，d为孔径）。其中β的影响规律比较简单，即压损系数随β增大而减小[4-11]，而孔数与孔厚对多孔板压损系数的影响机理仍不清楚。

关于孔厚对多孔板压损系数的影响，Malavasi等[7]在相同的β、n和孔分布条件下改变t/d发现，在0.24≤t/d≤1.4时，压损系数随t/d增加呈波浪状变化。在Holt 等[8]对多孔板压损系数的实验研究中，将孔数的影响归因于t/d变化，由其实验结果认为，随t/d增大多孔板压损系数先减小后略有增大，临界t/d为1.5～2.0。Holt 等[8]强调t/d对多孔板压损系数具有显著影响，t/d=1.5多孔板的压损系数较t/d=0.25的多孔板下降约53%。

关于孔数对多孔板压损系数的影响，Özahi[9]在孔厚t和孔径d不变的条件下，在n为5～26时，改变孔数进行实验，得出压损系数随n增加而减小；但在n增加的同时β减小，因而其压损系数的减小可能更多是由于β减小所致。Malavasi 等[7]和Zhao等[10]的实验是在相同β和孔厚t下，研究压损系数随n增加的变化，结论均为压损系数随n增加而减小。同样Malavasi等[7]和Zhao等[10]就n的影响进行比较得到，在n增加的同时t/d增大，因而其压损系数的减小也可能是t/d增大所致。

可见已有的研究中，关于相对孔厚t/d对多孔板压损系数影响的结论并不一致；而且以往研究在分析孔数n对多孔板压损系数的影响时，未能剔除β和t/d的影响，故所得结论不能准确反映n的影响。由于孔数与孔厚的影响机理仍不清晰，在现有的多孔板压损系数关联式模型中，有的只考虑了β的影响，有的只考虑了β和t/d的影响[11]。因此探明孔数与孔厚对多孔板压损系数的影响机理，是建立准确可靠的多孔板压损系数关联式的关键。本文以多孔板均匀布孔为前提条件，以β=0.40 为例，通过数值模拟方法分别对相同孔厚t-不同孔数、相同孔数-不同相对厚度t/d、相同t/d-不同孔数3 种情况下的多孔板压损系数进行计算与分析。

1 研究内容与孔板结构参数设计

1.1 研究内容设计

图1 多孔板结构示意图

多孔板的结构参数如图1所示。本文首先对工程应用中常见的在相同的β和孔厚t下改变孔数n的情况进行研究，获得多孔板压损系数随n的变化规律。在这种情况下，由以往的研究已知随n增大压损系数是先减小后趋于稳定值，但对于使压损系数达到稳定值的最小临界孔数仍不清楚。为了探究最小临界孔数是否随管径D的变化而改变，本文取D=100mm 和D=50mm 分别研究其临界孔数。由此可获得在常见的多孔板应用（β、t不变）中改变n对压损系数的影响以及临界孔数与D的关系。继而，对相同β和n下改变t/d、相同β和t/d下改变n的两种情况进行研究，分别获得t/d和n对压损系数的影响及其规律，从而说明t/d与n各自对多孔板压损系数的影响机理。

1.2 孔板结构参数设计

多孔板的开孔方式多种多样（例如按同心圆布孔、分形孔板等），这进一步增大了多孔板压损系数结果的分散性。已有研究也表明孔分布形式不同对多孔板压损系数有影响[10,12]。本文为避免孔分布形式不同的干扰，所研究的多孔板以小孔呈正三角形布置，均匀布满整个孔板且以孔板中心对称布孔为原则。

在均匀布孔条件下，本文模拟计算的孔板的n为1、4、10、14、38 和64，t/d为0.1、0.25、0.5、1.0、1.5和2.0。在不同管径下，各孔板的孔分布位置相同，各孔板的小孔分布情况如图2所示。在相同β、t下改变n的研究所模拟的孔板结构参数见表1，在相同β、t/d下改变n的研究所模拟的孔板结构参数见表2，共计模拟计算了39个孔板试件。

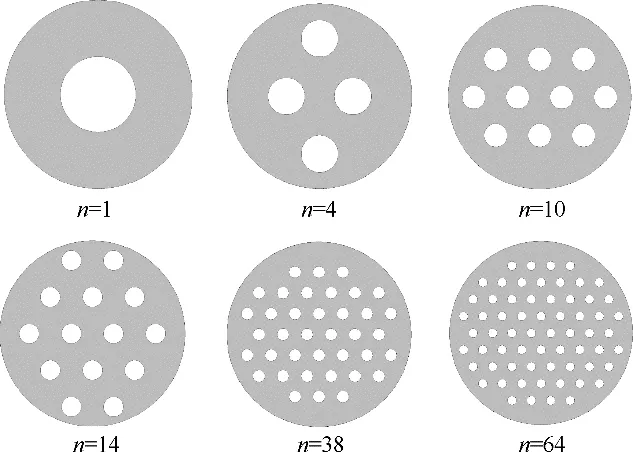
图2 在不同孔数下孔板的孔分布

2 数值计算模型

2.1 计算区域与网格划分

各孔板试件的流体计算区域如图3所示。为使管内流动充分发展后流经孔板，孔板上游管段长度取5D。由模拟结果可知，流体静压在孔板之后3D以内可恢复至稳定值。考虑到孔板之后的流动需恢复至稳定的问题，下游管段长度取10D。

表1 在相同β、t下改变n的孔板模拟试件（β=0.40）

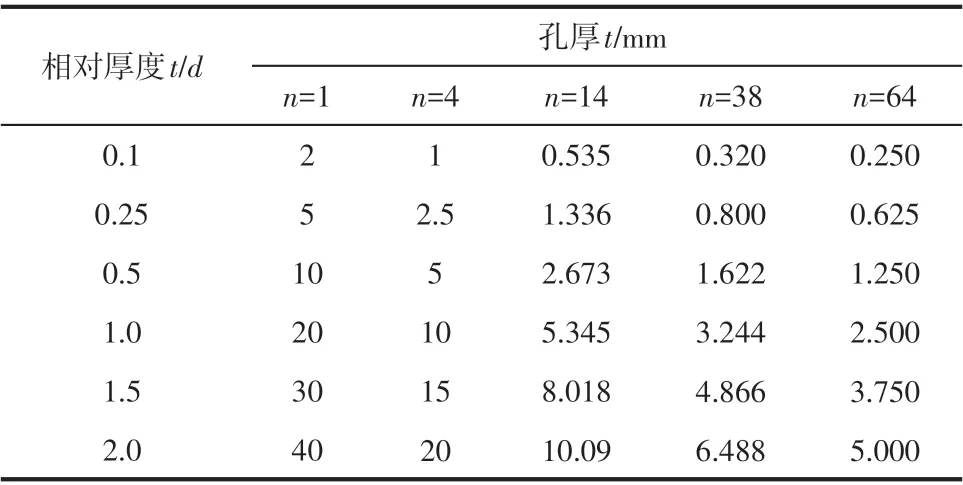
表2 在相同t/d下改变n时孔板试件的孔厚t（β=0.40）

图3 计算区域及网格

网格独立性验证：在Re=1.0×105时，对D=100mm管道中的n=1和n=14孔板分别在4个不同网格数（61 万、385 万、521 万和653 万）下进行数值计算，得到孔板压降随网格数的变化如图4。因此本文采用521万网格的划分方法。

图4 网格独立性验证

2.2 控制方程

根据管内水流经孔板实际流动状况，做如下假设：①流体与壁面之间无热交换；②流体不可压缩，即Dρ/Dt=0；③流动为稳态，即∂/∂t=0。故描述计算域内单相不可压缩流体稳态流动的基本方程为式(1)和式(2)。

连续方程

雷诺平均N-S方程

式中，下角标i、j为张量指标，取值为1、2、3；u、p、ρ、μ、μt分别为流体的速度、压力、密度、动力黏度、湍流黏度。式(2)中湍流黏度的封闭采用标准k-ε模型，其方程见Fluent手册[13]。

2.3 数值解法与边界条件

采用有限体积法离散化控制方程，由Simple算法解决压力与速度的耦合关系，近壁区流动采用壁面函数法处理。欠松弛因子为：压力0.3、速度0.7、湍动能耗散率0.8，其他为1。在上述条件下，方程组采用分离、隐式求解，获得收敛（残差不大于1×10-4）。利用Fluent 软件进行计算，获得管道内流场与静压分布。

边界条件：管壁与孔板为无滑移壁面，管内流体为常温水，入口条件为速度进口，流速为1m/s，出口条件为压力出口，出口表压为0。

2.4 数值计算结果处理方法

孔板压损系数ξ定义如式(3)。

式中，Δp为孔板的永久性压力损失，Pa，根据国家标准GB/T 2624.2—2006[14]，是孔板上游距离孔板1D位置静压与孔板下游6D位置静压之差；ρ为水的密度，kg/m3，本文中ρ=998.2kg/m3；u为管道来流速度，m/s，本文中u=1m/s。

根据雷诺数定义Re=uD/v（v为水的运动黏度，v=1.004×10-6m2/s），u=1m/s 时，D=100mm、D=50mm管道内流体的Re分别为9.96×104和4.98×104。随着来流Re增大，孔板压损系数会逐渐由变化值趋于定值，使压损系数达到稳定的最小Re称为稳定区临界雷诺数。经过数值模拟验证，本文所取的D=100mm、D=50mm管道内流体Re均已大于其稳定区临界Re，所以本文模拟所得结果均为孔板的稳定区压损系数。

2.5 数值模拟方法的实验验证

本文作者课题组蔡振琦[15]在D=100mm 管道内对单相水流经等效直径比0.4、孔板厚度5mm 单孔板的压降特性做了实验研究，获得其稳定区压损系数为80.5。通过本文数值模拟方法，在管道及孔板结构参数均保持与实验相同的条件下，计算出该孔板的稳定区压损系数为75.5。实验值与模拟值的偏差为6.2%，表明本文模拟方法及结果准确可信。

3 数值计算结果及分析

3.1 相同β、t下改变n对孔板压损系数的影响

在相同的β、t下，孔数n对孔板压损系数ξ的影响如图5所示。

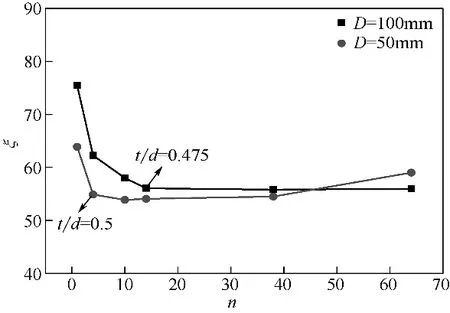
图5 相同孔厚下孔数变化对孔板压损系数的影响

由图5 可知，在相同的β、t下，ξ随n增大而先减小后趋于定值。在D=100mm 管道中使ξ达到稳定的临界孔数为14左右，在D=50mm管道中使ξ达到稳定的临界孔数为4左右，也即临界孔数随D减小而减少。可见在β、t保持不变时，在n小于临界孔数的区域ξ确实随n增大而减小，这符合以往认为增大n可使ξ减小的一般认识。但在n大于临界孔数的区域，ξ并不随n增大而减小，意味着此时增大n不会减小孔板节流压损效益。由D=50mm管道中n=38 和n=64 孔板的ξ比较可知，过多地增大n还会使ξ趋于缓慢增大。

在相同β、t下增大n意味着孔口相对厚度t/d增大，如表1 所示。所以此时ξ随n增大而减少的结果究竟是由t/d增大引起还是由n增大引起并不清楚。值得注意的是，由图5 可见，虽然D=100mm和D=50mm管道的临界孔数明显不同，但二者在临界孔数下的t/d非常接近，均在t/d=0.5附近，这说明t/d减小很可能是导致ξ减小的主要原因。总体来看，在相同的β、t下，多孔板ξ可较单孔板ξ降低20%左右。

3.2 相对厚度对多孔板压损系数的影响

在D=50mm 管道中，取β=0.4 不变，通过数值计算模拟表2 所示的孔板试件，可得相对厚度t/d对压损系数ξ的影响如图6所示。

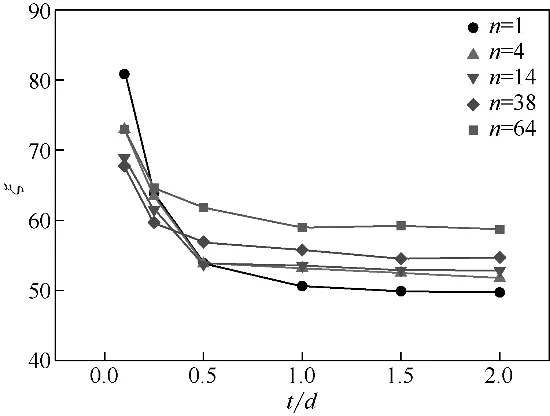
图6 相对厚度变化对孔板压损系数的影响

由图6可知，在相同的β、n下，ξ随t/d增大先减小后趋于定值，这与以往关于t/d对单孔板ξ的影响是一致的。可见，使ξ达到稳定的临界t/d在1.0附近。即在t/d＜1.0 时，ξ随t/d增大而快速减小；在t/d≥1.0 时，随t/d增大ξ基本不变。如图7 所示，这是因为在薄孔板（t/d＜1.0）中，随t/d减小，流体在孔口处的收缩增强（即收缩系数减小），射流核心区流速增大，使孔板后回流涡流的黏性耗散增大所致；而在厚孔板（t/d≥1.0）中，由于流体在孔道内经历第一次膨胀（收缩系数接近1.0），在相同流量和β下孔口射流速度基本不变，故孔板后回流涡流的黏性损失随t/d增大也基本不变。

图7 n=1孔板在不同相对厚度下的流动特性

图6所示结果表明，在薄孔板中t/d对ξ具有显著影响，但其对ξ的影响程度随n增大而逐渐减弱。例如n=1 时，厚孔板（t/d≥1.0）的ξ较t/d=0.1 孔板的ξ下降38%；而n=64 时，厚孔板（t/d≥1.0）的ξ较t/d=0.1 孔板的ξ下降19%。这是因为在相同β下，随n增大孔径d趋于减小，因而孔口射流的射程随d减小而减小，如图8所示。射程减小使孔板后回流涡流的区域减小，因而射流核心的速度变化对孔板流动损失的影响减弱，因此表现为随n增大，t/d变化对ξ的影响趋于减小。

3.3 相同β、t/d下改变n对孔板压损系数的影响

将表2 所示孔板试件的模拟结果整理为孔数n对孔板压损系数ξ的影响，结果如图9 所示。由图9 可知，在相同的β、t/d下，n对ξ的影响规律随薄、厚孔板之分而不同。在t/d≤0.5 的薄孔板中，随n增大ξ呈先减小后增大趋势，而且n对ξ的这种影响随t/d减小而愈加明显；而在t/d≥1.0 的厚孔板中，随n增大ξ缓慢增大。这表明工程应用中的一般认识“增大n从而减小ξ”在厚孔板中并不成立，在薄孔板中只在一定孔数范围内成立。同时也说明t/d=0.5～1.0是薄、厚孔板之分的过渡区域，薄、厚孔板中流体流动特性的差异，使n对ξ的影响表现出不同规律。

图8 n=14孔板在不同相对厚度下的流动特性

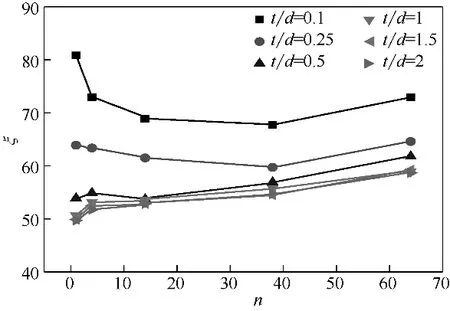
图9 不同相对厚度下压损系数随孔数变化图

在薄孔板中由于流体收缩明显，射流核心区在孔板后。由图10可见，在n较少的区域，随n增大射流长度明显变小，因而板后回流涡流区域变小，ξ也相应减小。但在一定的n（对D=50mm 管道n=38，此时d=3.25mm）之后随n进一步增大，射流长度减小不明显，但由于射流的数量增多，射流卷吸的总面积增大，使得孔板流动的黏性损失趋于增大，表现为随n增大ξ缓慢增大。

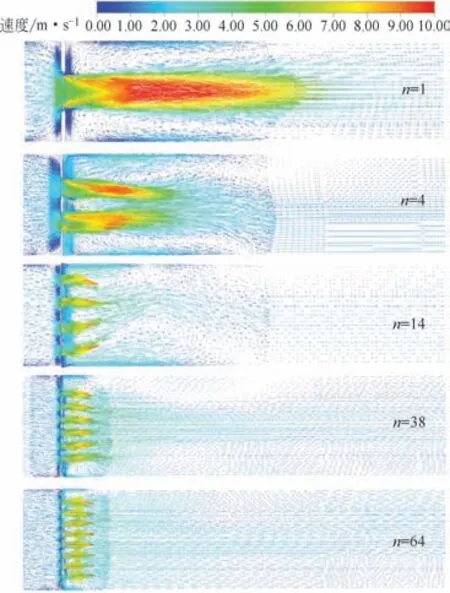
图10 t/d=0.1孔板在不同孔数下的流动特性

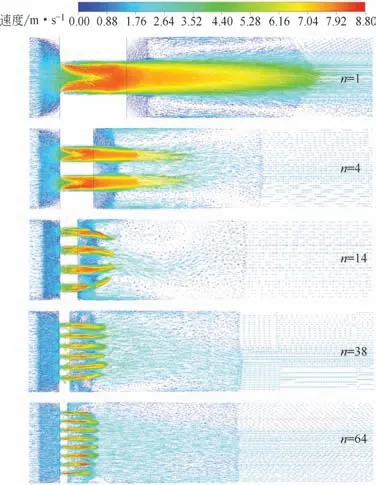
图11 t/d=2.0孔板在不同孔数下的流动特性

在厚孔板中由于流体在孔道内发生膨胀，与薄孔板相比射流的最大速度减小，同时大部分射流核心区转移至孔道内，如图11所示。在相同流量和β下，厚孔板的孔口射流速度基本不变，因而孔板后回流涡流的黏性损失变化不大。但由于d随n增大而减小，此时孔道对流体的黏性摩擦作用也成为影响ξ大小的重要因素。因此在相同β下，厚孔板的ξ随n增大总是逐渐增大。

由图9 可知，在t/d=0.1 的薄孔板中，随n从1增大至38，ξ降低了16.2%；在t/d=2.0 的厚孔板中，随n从1增大至64，ξ升高了15.7%。可见在本文研究的n=1～64时，无论薄孔板或厚孔板，ξ随n变化而改变的幅度约为16%。这表明n对ξ的影响不容忽视，在多孔板ξ关联式模型中应包含n的影响。此外，这也说明图5所示的ξ随n增大而减小结果中，既包含t/d增大的贡献，也包含n增大的贡献。

4 结论

在一定的等效开孔直径比下，通过数值模拟方法研究了孔数与孔厚对均匀布孔多孔板的稳定区压损系数的影响机理，结论如下。

（1）在相同的孔板厚度5mm下，随孔数从1增加至64，压损系数先快速减小后趋于不变，使压损系数达到稳定的临界孔数随管径减小而减少，但临界孔数对应的孔板相对厚度均接近0.50。

（2）在相同的孔数下，随孔板相对厚度从0.10增加至2.0，压损系数先快速降低后趋于不变，降幅为19%～38%。使压损系数达到稳定的临界相对厚度为0.5～1.0，临界相对厚度随孔数增多而减小。

（3）在相同的相对厚度下，薄孔板的压损系数随孔数增多先减小后增大，而厚孔板的压损系数随孔数增多单调增大。在孔数1～64时，压损系数随孔数变化而改变的幅度约为15%。

（4）除等效直径比外，孔数与孔板相对厚度均对多孔板压损系数有影响，应在压损系数关联式模型中予以考虑。