基于安定分析和概率密度演化理论的杆系结构整体可靠度分析

祖云飞，李正良，2，范文亮，2，刘蜀宇

（1. 重庆大学 土木工程学院，重庆400045；2. 重庆大学山地城镇建设与新技术教育部重点实验室，重庆400045；3. 顺泰铁塔制造有限公司，重庆400000）

由于工程结构自身及其所处环境存在各种不确定性，可靠度分析成为结构安全性评估的重要方法[1]，其中经典的体系可靠度是重要组成部分.不同于构件可靠度，经典的体系可靠度主要研究理想弹塑性或弹脆性杆系结构在静力荷载作用下的不倒概率，即结构整体不发生倒塌的概率.历经半个多世纪的发展，研究者提出了PNET 法、分支约界法、优化准则法、最小荷载增量法等分析方法[2-5].仔细考察不难发现，经典体系可靠度仅涉及时不变的静力荷载，即量值保持不变的静力荷载；然而，实际工程中结构亦可能会遭遇另一类静力荷载——量值随时间变化的时变静力荷载.例如，输电导线的覆冰荷载，由于结冰、融冰过程的缓变特性，以及可能出现的冻融循环，属于典型的变值静力荷载；又如储油罐对其支撑刚架的作用亦属于变值静力荷载.

杆系结构在变值静力荷载作用下可能的最终破坏状态包括增量塑性破坏、交互塑性破坏、瞬时塑性倒塌破坏[6]，若仍采用经典的体系可靠度方法研究结构安全，实质上仅考虑结构的不倒概率，忽略了结构可能的最终破坏状态中的交互塑性破坏. 当发生交互塑性破坏时，结构中出现断裂杆件，不同于杆件进入塑性，杆件的断裂使杆件完全退出承载，随之产生的内力重分布引发多米诺效应可能导致结构整体倒塌.即使杆件断裂后结构依然能保持不倒，断裂杆件的更换仍会影响结构正常服役.因此，采用经典的体系可靠度研究变值静力荷载下杆系结构的安全性是不合理的，低估了结构面临的风险.

幸运的是，安定理论[6-8]为研究变值荷载作用下结构行为提供了有效工具.近年来，研究者对基于经典安定理论的结构可靠度分析开展了一系列研究，亦取得了一定的进展[9-14]，然而现有成果存在较大的局限性：一方面，由于与FORM[10，12-14]、SORM[12]及响应面法[11]等基于验算点的可靠度方法相结合，对于体系可靠度中出现的多验算点问题无能为力；另一方面，现有研究通常针对已知的失效模式进行安定分析，但失效模式识别恰恰是复杂杆系结构体系可靠度分析的最大困难，因此，现有研究多局限于平板结构[10，14]、压力容器[11，13，14]、管道结构[10，12-14]以及非常简单的杆系结构[11，13，14]等，实用性不强.

鉴于此，本文以安定状态作为杆系结构在变值静力荷载作用下的极限状态，并定义与之对应的整体可靠度概念，建议了具有单一功能函数的极限状态方程，并引入实用安定分析方法计算隐式功能函数；进而，根据概率密度演化理论，推导了功能函数的广义密度演化方程的近似解；最后，经由一维积分给出结构整体可靠度.本文将安定分析与概率密度演化理论[15]相结合，提出了杆系结构在变值静力荷载作用下整体可靠度的实用、高效分析方法.尤其值得指出的是，经典体系可靠度所涉及的时不变的静力荷载仅为变值静力荷载中的一种特殊情况，显然，本文建议方法同样可解决经典的体系可靠度问题.因此，发展基于安定理论的结构整体安全性分析既是解决变值静力荷载作用下理想弹塑性杆系结构整体可靠度的合理途径，亦是经典体系可靠度的有益拓展.

1 杆系结构的安定极限状态及确定性安定分析

1.1 变值荷载作用下结构的临界极限状态

根据安定理论，杆系结构在变值荷载作用下可能进入五种不同的状态[6]：1）纯弹性状态；2）安定状态；3）增量塑性破坏；4）交互塑性破坏；5）瞬时塑性倒塌.由于增量塑性破坏和瞬时塑性倒塌将引起结构的整体倒塌，而发生交互塑性破坏时，尽管结构可能维持不倒，但断裂杆件的更换会迫使结构退出正常工作.因此，世界各国近年来出版的强度设计与安全设计评定规范（如美国ASME 和API 规范、英国BSI标准、法国RCC-MR 标准等），越来越多地采用安定载荷为控制界限的塑性失效准则.因此，本文定义增量塑性破坏、交互塑性破坏和瞬时塑性倒塌为结构的三种最终破坏状态，定义结构在变值荷载作用下不进入上述破坏状态的概率为整体可靠度. 又因上述破坏状态均以安定状态为临界过渡状态，所以安定状态可作为杆系结构在变值荷载作用下失效分析的临界极限状态.

1.2 结构确定性安定分析

1.2.1 安定极限状态方程

若定义λ 为外荷载的比例系数，安定状态的临界荷载系数λp为恰使结构维持安定状态的λ 值，安定状态的极限状态方程可表示为

式中：G 为结构功能函数的值，当G ＞0 时，λp＞1，意味着结构达到安定状态所能承受的荷载大于实际外荷载，结构安全；反之，结构失效.因此，λp的确定是判断结构状态的核心.

1.2.2 λp的确定

根据安定下限定理，λp可由如下优化问题确定

式中：ρ 表示与时间无关的自平衡残余应力场，S（t）表示将结构假定为纯弹性后的应力场，f（·）表示材料屈服条件；CT为结构总平衡矩阵，在小变形假设下，仅取决于结构体系的几何关系[16-17]，CTρ=0 表示残余力系自平衡方程.

由于屈服约束条件（fρ+λS（t））≤σ 包含时变的S（t），式（2）所示优化问题不便于直接求解.文献[18-21]指出，若结构的荷载变化域为凸域，且在变化域的所有顶点上结构均保持安定状态，则结构在该荷载变化域内任一变值荷载作用下亦能保持安定状态，于是式（2）可改写为

式中：Pk表示荷载变化域的第k 个顶点，Nl为顶点的总数，S（Pk）表示结构在Pk所对应的时不变荷载下的应力场，显然式（3）为时不变的优化问题.

若假设结构承受d 个相互独立的变值荷载，且第i 个变值荷载的上、下界值分别为ai，bi（i=1，…，d），则这些荷载变化的凸域包含Nl=2d个顶点，且有

图1 给出了仅有两个变值荷载时的凸域及顶点示意图.根据线性叠加原理，可有

式中：S（Fei）表示结构在与第i 个变值荷载作用位置和正方向相同的单位力Fei作用下的应力场.显然，仅需得到各变值荷载对应单位力下的应力场S（Fei），（i=1，2，...，d），S（Pk）可根据式（6）由代数运算直接得到，因此，尽管存在2d个顶点，求解S（Pk）所需的线弹性结构响应分析次数仅为d 次.

图1 荷载变化域及其顶点Pk（d=2）Fig.1 The load variation domain and vertices Pk（d=2）

得到S（Pk）后，求解式（3）所示优化问题还需确定CT的具体参数.在经典安定分析中CT常根据结构的失效模式由运动机构分析法得到[6].显然上述方法仅适用于运动机构（失效模式）已知的简单情况.近年来，有限单元法由于其适用性强，便于计算机进一步分析等优点，成为确定CT的主流方法[9-14]，由有限单元法建立CT与结构系统总刚矩阵的建立过程类似，首先根据单元类型以及单元基本内力参数在局部坐标系下建立单元平衡矩阵，对于本文研究的杆系结构，其单元平衡矩阵建立过程可参考文献[16，17]，然后考虑各单元之间的几何连接关系以及边界条件，按结构矩阵分析理论在全局坐标系下组装各单位平衡矩阵即可得到总平衡矩阵CT.

上述确定CT的方法通常需通过自编程实现，较为繁琐. 对于常见的桁架结构和平面抗弯刚架结构等两类杆系结构，可基于虚力法建立与式（3）等价但更易于实现的优化问题.

对于M 杆的理想弹塑性空间桁架，根据虚力法，式（3）可改写为[21]：

式（7）表示桁架的拉压屈服条件，即为式（3）中材料屈服条件f（·）在此情况下的具体形式，其中ρm是第m 杆的残余轴向应力，Smaxm，Sminm分别表示假定结构为纯弹性后考虑所有可能荷载时程组合条件下第m 杆的最大纯弹性拉应力和压应力，其可由式（9）计算得到，Sm（Pk）为顶点Pk所对应条件下第m 杆的纯弹性轴向应力，其可由式（6）所示线性叠加得到.σm、σm′是第m 杆的全塑性抗拉强度和全塑性抗压强度.式（8）为由虚力法得到的CTρ=0 的等价虚功方程组，其中lm表示第m 杆的长度，Svmj表示由第j 个虚力所引起的第m 杆内的轴向应力，Em表示第m 杆的弹性模量，lmSvmj/Em表示第m 杆的虚位移，等于其在第j个虚力下对应的弹性变形，式（8）中虚力为对应于某个节点位移自由度方向的单位力，其总数Ns等于节点位移自由度总数，因此，式（8）中各参数的确定需Ns次结构响应分析.

对于由理想弹塑性材料构成的平面抗弯刚架，根据虚力法，式（3）可改写为[22，23]：

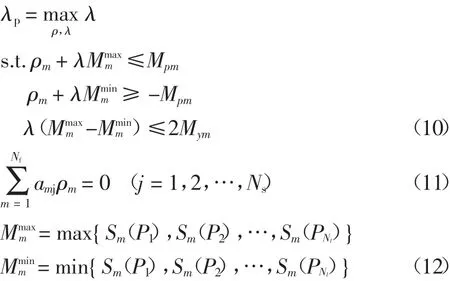
式（10）表示刚架的受弯屈服条件，同样为式（3）中材料屈服条件f（·）在此情况下的具体形式，其中ρm为第m 个塑性铰的残余弯矩，Mmaxm，Mminm分别表示假定结构为纯弹性后，考虑所有可能荷载时程组合条件下第m 个塑性铰的最大纯弹性弯矩和最小纯弹性弯矩，其由式（12）计算得到，Sm（Pk）为顶点Pk所对应条件下第m 个塑性铰的弯矩，其同样可由式（6）所示线性叠加得到.Mpm是第m 个塑性铰的全塑性极限弯矩，Mym是第m 个塑性铰仅截面外边缘屈服的弹性极限弯矩.式（11）为由虚力法得到的CTρ=0 的等价虚功方程组，amj为对应于在第j 个虚力作用下第m 个塑性铰的系数，其取值方法详见文献[22]，Nf为预定义的可能塑性铰的总数.Ns为对应刚架全部基本变形的所有虚力的总数，其与结构自由度正相关，Ns和各虚力的施加方式由文献[22]给出的三个准则确定，因此，式（11）中各参数的确定需Ns次结构响应分析.

综上所述，λp可由式（3）所示优化分析得到，而式（3）中的残余力系自平衡方程CTρ=0，可由有限单元法得到或虚力法建立其等价虚功方程组. 虚力法可以避免有限单元法自编程建模型的繁琐过程，但将引入额外的结构分析.因此，选择虚力法或是有限单元法应根据分析结构的自由度总数进行权衡，在结构自由度总数较高时，宜选择有限单元法.

1.3 λp 的求解步骤

根据1.2 节的分析，杆系结构λp可按下述步骤求解：

①对各变值荷载对应的单位力Fei作用下的结构进行受力分析，得到应力场S（Fei），（i=1，2，...，d）.将S（Fei）代入式（6）由代数运算得到结构在各顶点Pk对应的时不变荷载条件下的响应应力场S（Pk），本步骤所需线弹性结构受力分析次数为d 次.

②建立残余力系自平衡方程.若直接基于CTρ=0，则需通过自编程序确定C 矩阵；若采用虚力法，则可引入有限次附加结构分析得到CTρ=0 的等价虚功方程组式（8）或式（11）.

③采用MATLAB 优化求解工具箱求解相应的优化问题，得到临界安定荷载系数λp.

2 基于概率密度演化理论的杆系结构整体可靠度分析

2.1 考虑随机性的安定极限状态方程

在安定分析中，尽管结构承受时变荷载，但由式（3）可知，λp仅取决于结构参数、时不变荷载以及时变荷载的时不变参数.显然，当结构参数及外荷载具有随机性时，λp可表示为随机量的函数，即

式中：随机向量Θ=（Θs，ΘLO），Θs=（Θ1，Θ2，…，Θs1）表示随机结构参数，ΘLO=（Θs1+1，Θs1+2，…，Θs1+s2）表示时不变的随机荷载；Pk为变值荷载域的随机顶点，取决于描述变值荷载上下界的时不变随机参数ΘLR，即

将式（13）和式（14）代入式（1）可得考虑随机性的安定极限状态方程为

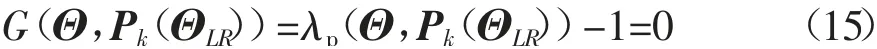
由于仅涉及一个极限状态方程，经典体系可靠度分析中存在的失效模式相关性问题迎刃而解.进而，结构整体可靠度为

式中：pG（g）指随机变量G=G（Θ，Pk（ΘLR））的概率密度函数.显然，可靠度R 对应的失效概率为1-R.

2.2 整体可靠度的概率密度演化分析

概率密度演化理论为获得pG（g）的数值解提供了可行的途径.

首先，构造虚拟随机过程Z（τ）

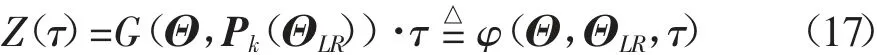
类似于随机动力系统的广义密度演化方程的推导[15]，（Z（τ），Θ，ΘLR）联合密度函数PZΘΘLR（z，θ，θLR，τ）服从如下方程

其初始条件为

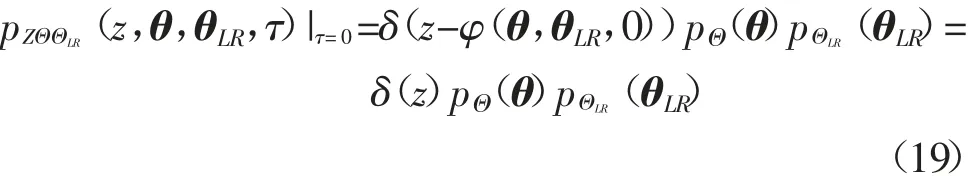
式中：δ（·）为狄拉克函数，PΘ（θ）是Θ 的概率密度函数，PΘLR（θLR）为ΘLR的概率密度函数.引入特征线法[24]可导出式（18）和式（19）的形式解析解[25]为

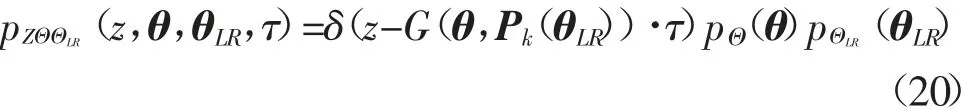
结合式（17）可知

式中：ΩΘ为Θ 的分布域，ΩΘLR为ΘLR的分布域.为避免广义函数δ（·）的直接积分，可以δ 序列替代δ（·）获得pG（g）近似解为[25]

式中：φmax=max {φ（θ，θLR，τ）|τ=1}=max {G（θ，Pk（θLR））}，α 为一适当小的常量. 进一步可给出其数值解为

式中：代表点集（θq，θLR，q）（q=1，…，Nsel）可由数论选点策略[26]得到，同时给出其赋得概率为Uq，其中Nsel为代表点的数量.

2.3 杆系结构整体可靠度的数值实现

综上所述，基于安定理论的结构整体可靠度数值求解步骤如下：

①由数论选点策略[26]在多维联合变量空间（Θ，ΘLR）中选取代表点集（θq，θLR，q）（q=1，…，Nsel），并得到各代表点的赋得概率Uq.当（Θ，ΘLR）为相关向量且仅已知各变量的边缘概率密度函数和相关系数矩阵时，可以引入Nataf 逆变换[27]进行处理.

②对于给定代表点（θq，θLR，q），由2.3 节所述步骤确定λp，进而确定功能函数值G（θq，Pk（θLR，q）），重复以上步骤，求得所有代表点的功能函数值.

③将上述所有G（θq，Pk（θLR，q））（q=1，…，Nsel）及Uq代入式（23），得到pG（g）的数值解.

④将pG（g）的解代入式（16），由一维数值积分即可得到结构整体可靠度R.

3 算例分析

本节由三个算例验证建议方法的有效性.算例1为一涉及六杆桁架结构的经典体系可靠度问题，通过建议方法结果与已有结果的对比验证建议方法的准确性和效率；算例2 以单层两跨平面抗弯刚架结构为对象，比较了时不变静力荷载下的经典体系可靠度与时变静力荷载下的整体可靠度的差异，验证了建议方法的必要性；算例3 采用建议方法分析了相对较为复杂的空间二十五杆桁架，体现了建议方法的普遍适用性.

3.1 算例1

某六杆桁架如图2 所示，其1、2、5、6 杆的截面积为1.33×10-4m2，3、4 杆的截面积为1.49×10-4m2.各杆由理想弹塑性材料组成，其初始弹性模量为2.06× 105MPa；F 为随机时不变荷载，σm（m=1，2，…，6）为第m 杆的随机屈服强度，随机变量的概率信息如表1 所示，且假设各变量均相互独立.对该桁架的不倒概率进行分析.

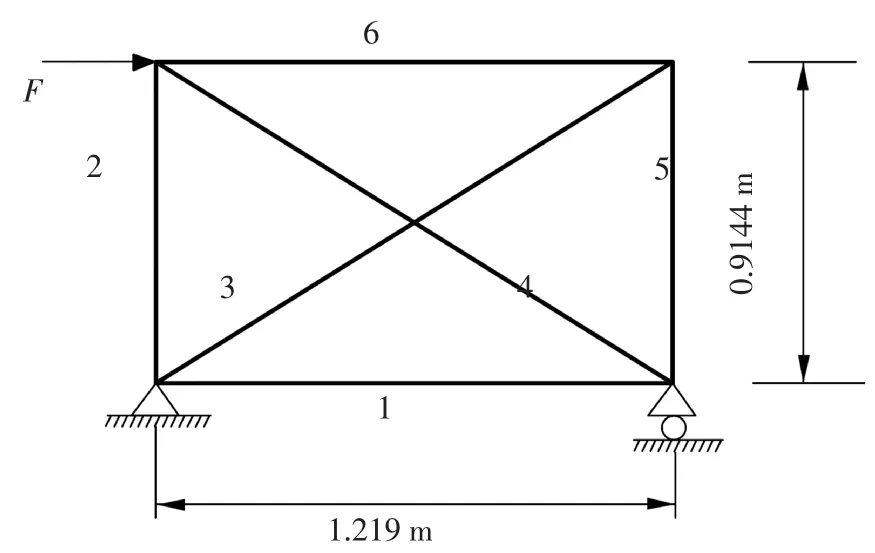
图2 6 杆桁架Fig.2 A 6-bar truss

表1 算例1 中随机变量的概率信息Tab.1 The statistical information of random variables involved in example 1

显然，该问题属于经典的体系可靠度问题，但亦可用建议方法求解.

首先，利用数论选点策略在F 和σm组成的七维随机向量空间中选取1 752 个代表点，并得到各代表点的赋得概率Uq（q=1，2，…，1 752）.然后，对于任一代表点，均可由前述的确定性安定分析得到对应的功能函数值G（θq，Pk（θLR，q））.不难发现，确定性安定分析的屈服约束条件仅由结构的线性分析确定，而对于此结构1 752 个代表点对应着相同的线性结构，换言之，仅需1 次线性结构分析即可确定所有代表点的屈服约束条件. 若采用虚力法以避免残余力系自平衡方程CTρ=0 的建立，尚需补充4 次线性结构分析. 由于采用虚力法总共仅需5 次线性结构分析，较直接建立CTρ=0 更为简便，因此，此处采用虚力法.获得所有样本点的功能函数值后，可由式（23）得到功能函数概率密度函数的数值解pG（g），其中参数α 由文献[25]中所述方法确定，其值为0.005 5，求得的pG（g）如图3 所示.最后，由式（16）得到结构的经典体系可靠度，其对应失效概率为5.64×10-4.此外，文献[28]给出了近似解为5.92×10-4，文献[29]给出的失效概率上下界限为[5.02×10-4，7.16×10-4].显然，建议方法所得结果是合理、有效的.由于涉及很少的线性结构分析和非常成熟高效的线性优化问题的求解，建议方法的高效性是显而易见的.

图3 6 杆桁架的概率密度分布pG（g）Fig.3 Probability density function of G for the 6-bar truss

3.2 算例2

某一承受F1，F2和F3三个外荷载的理想弹塑性材料组成的单层两跨平面抗弯刚架如图4 所示，其中，各杆截面相同，Mp为截面全塑性极限弯矩，而截面弹性极限弯矩为0.8Mp，结构可能的塑性铰总数为11.F2和F3为随机时不变荷载，根据F1特性的不同，分为以下2 种情况.

图4 单层两跨平面刚架Fig.4 A 1-story and 2-bay plane frame

情形1：F1为随机变值静力荷载

假定a1和b1分别为F1的下界和上界，随机变量的概率信息如表2 所示，且假设各变量相互独立.分析结构在变值荷载作用下的整体可靠度.

按建议方法选取分析968 个代表点，并确定参数α=0.002 2，得到近似概率密度分布pG（g）如图5所示，对其积分得到结构整体可靠度对应的失效概率为8.16×10-4.同样，上述过程中所有代表点的确定性安定分析屈服约束条件由3 次线性结构分析确定，而CTρ=0 的等价虚功方程组由虚力法补充2 次线性结构分析得到.此外，将简单蒙特卡罗法与确定性安定分析结合，对106个样本点分析后得到失效概率为8.47×10-4. 上述两结果的相对差异为（8.47-8.16）/8.47=3.66%，显然，建议方法的高效性和准确性再次得到验证.

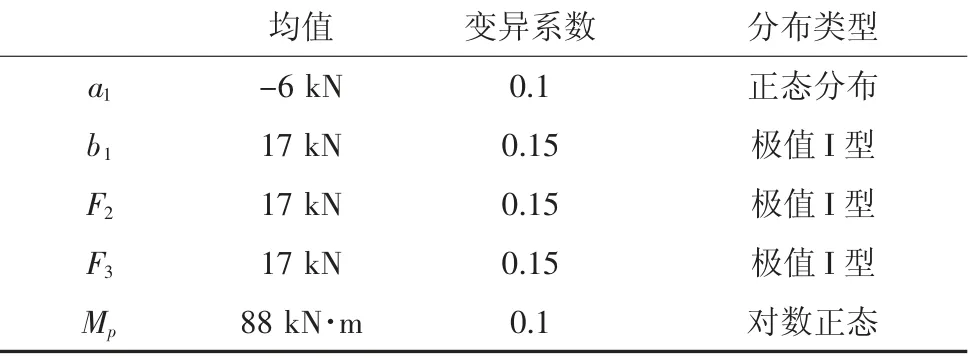
表2 算例2 中随机变量的概率信息Tab.2 The statistical information of random variables involved in example 2

图5 情形1 中平面刚架的概率密度分布pG（g）Fig.5 Probability density function of G for the plane frame in case 1

情形2：F1为随机时不变静力荷载

在本情形中，F1假定为随机时不变静力荷载，其统计信息与情形1 的上界值b1相同. 其余条件与情形1 相同.分析结构的不倒概率.

在本情形中，按建议方法选取分析641 个代表点，并确定参数α=0.002 0，得到pG（g）的概率密度分布如图6 所示，对其积分得到结构整体可靠度对应的失效概率为4.73×10-4.

另外，采用抽样数为106 的蒙特卡罗法可得到结构失效概率为4.89×10-4.上述两结果高度吻合.

比较情形1 和情形2 的计算结果不难发现，结构在变值荷载作用下的整体可靠度并不等于其在时不变静荷载（取变值荷载的上界）作用下的不倒概率，甚至较后者更低.因此，建议方法所得整体可靠度能更合理地评估变值静力荷载作用下结构的安全性.

图6 情形2 中平面刚架的概率密度分布pG（g）Fig.6 Probability density function of G for the plane frame in case 2

3.3 算例3

某25 杆理想弹塑性空间桁架结构如图7 所示，材料初始弹性模量为2.06×105MPa，各杆属性如表3所示. 外荷载包括水平节点荷载F1和竖向节点荷载F2，其中F1为随机时不变荷载，F2为随机变值静力荷载；且假定F2的上界为b2，下界为X·b2，X 为一定值.σ 为材料的抗拉屈服强度，抗压屈服强度假定为0.9·σ.随机变量的概率信息如表4 所示，且假设各变量均相互独立.分析结构在变值荷载作用下的整体可靠度.

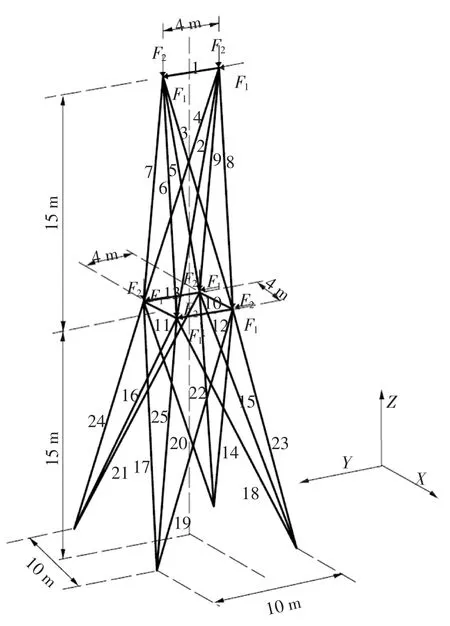
图7 25 杆空间桁架Fig.7 A 25-bar space truss

表3 25 桁架杆件属性表Tab.3 The attribute of all components for the 25-bar truss

表4 算例3 中随机变量的概率信息Tab.4 The statistical information of random variables involved in example 3

X 的不同取值对应于不同的变值静力荷载情形.特别地，当X=1 时F2退化为时不变静力荷载.

选取685 个代表点，采用建议方法分别对不同X 值的情形进行分析，得到近似概率密度分布pG（g）和结构失效概率如图8 和图9 所示（参数α 均为0.004 5）.上述过程中确定性安定分析的屈服约束条件由2 次线性结构分析得到，并由虚力法补充18 次线性结构分析得到CTρ=0 的等价虚功方程组.

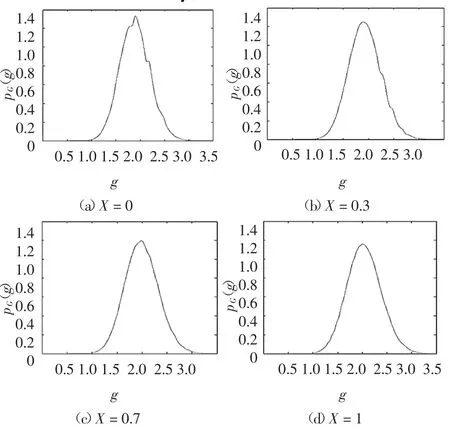
图8 不同X 取值时空间桁架的概率分布pG（g）Fig.8 Probability density function of G for the space truss with different X

图9 不同X 取值时空间桁架的失效概率Fig.9 The tendency of failure probability for the space truss with different X

由图9 可见，结构失效概率随着X 值增大而单调递减.换言之，若变值静力荷载上界保持不变，其变化范围越大，结构失效概率越大.

此外，对X=0 的情况，将简单蒙特卡洛法与确定性安定分析结合，当选取106 个样本点可得到结构失效概率为6.29×10-4，与建议方法结果的相对差异为（6.62-6.29）/6.29=5.2%，再次验证了建议方法的准确性.

4 结论

本文结合安定分析和概率密度演化理论，推导了以安定状态为极限状态的功能函数值G（Θ，Pk（ΘLR））的概率密度演化方程，并给出了其概率密度的数值求解方法.以此为基础，提出了一种可合理评估杆系结构在变值静力荷载作用下安全性的可靠度分析方法.并通过多个结构算例，验证了建议方法的精度和有效性，分析结果表明，建议方法无需进行失效模式的识别，从而避免了失效模式的组合爆炸问题；并且由于经典体系可靠度所涉及的时不变的静力荷载仅为变值静力荷载中的一种特殊情况，建议方法可直接应用于经典体系可靠度问题的分析；此外，建议方法所涉及计算大部分为线性优化求解，而线性优化求解的研究较成熟，大量已有的高效线性优化算法为建议方法的计算效率提供了坚实保障.值得指出的是，结构在变值荷载作用下的整体可靠度不同于其在时不变静荷载（取变值荷载的上界）作用下的不倒概率，因此应按建议方法评估变值静力荷载作用下结构的安全性.