快慢车组合运行条件下市域快线节能坡优化模型与算法研究

曹金铭，李得伟，董欣垒，于婕

快慢车组合运行条件下市域快线节能坡优化模型与算法研究

曹金铭，李得伟，董欣垒，于婕

(北京交通大学交通运输学院，北京 100044)

基于既有研究大多局限于站站停列车运行条件下的地铁节能坡优化，为解决快慢车组合运行条件下市域快线节能坡优化问题，在对列车受力分析的基础上，提出快慢车组合运行下列车运行能耗表达函数，并构建以运行能耗最小和列车运行时间偏离最小为目标的节能坡优化模型，并基于改进的遗传算法设计快速求解算法。通过广州市域快线18号线验证，研究结果表明：本文所提模型与算法能够有效求解节能坡设计方案，相对于原始方案，优化方案在保持运行时间小幅变动的前提下，使列车牵引能耗降低了15.2%~25.2%。并发现快慢车的不同比例对节能坡设计方案和节能效果有影响，慢车比例越大，方案的节能效果越显著。

市域快线；节能坡；遗传算法；快慢车组合运营

随着我国城市化、区域化进程的加快，连接城市中心与卫星城镇的大运量高速度的市域快线应运而生。市域快线作为城市轨道交通的一种制式，其速度高于地铁，站间距长，运营模式多为快慢车组合运行[1]。为了更好地节省列车能耗、实现城市轨道交通可持续发展，从线路纵断面优化设计角度考虑运营目标与列车能耗的相互协调，是一种长期且有效的方法[2]。节能坡优化设计问题在地铁线路设计中有较为广泛的研究基础，并在实际得到运用[3−4]，在高速铁路里也有少量研究[5−8]。对于市域快线，由于运行速度较高、部分列车存在跨站运行等特点，地铁节能坡设计理论无法直接应用。同样，由于线路性质不同、站间距不同，高速铁路节能坡的相关理论也不能用于市域快线。因此急需要一种适应于市域快线运输组织特点的节能坡优化设计方法。为了解决这一问题，本文研究提出了以列车牵引能耗最小和列车运行时间偏离最小为目标的节能坡优化模型，并设计改进的遗传算法，高效求解快慢车组合运行的市域快线线路节能坡优化方案。为市域快线的线路设计提供理论支持。

1 市域快线节能坡优化问题定义

1.1 市域快线节能坡优化的特殊性

与站站停模式的普速地铁不同，快慢车组合运行条件下市域快线的节能坡优化具有其特殊性，主要表现在以下2个方面：

1) 市域快线站间距长、运行速度高。市域快线站间距一般都在3 km以上，有些甚至超过了20 km，超过地铁2～3 km的站间距。国内外运营市域快线的最高运行速度在100～160 km/h，远远高于地铁60～70 km/h的运行速度。长站间距导致无法采用简单的加速−惰行−制动的节能运行方式。

2) 运营组织灵活，采用快慢车组合运行形式，快车在大站停车，在小站跨站不停车，慢车站站停车，并且当快车经过小站不停车时需要在安全限速内运行。不同类型的停站模式会导致同一个车站的节能坡对一种列车节能而对另一种列车不节能的情况。

1.2 节能与节时矛盾的处理

节能与节时是城市轨道交通节能坡设计追求的2个目标，既节能又节时的设计方案是最优化方案。事实上，节能与节时往往是矛盾的[6]，在市域快线条件下，这个矛盾更为突出。为了满足目标要求，在模型构建与算法设计时，在提升节能效果的基础上对节时进行约束，增加时间惩罚系数，从而完成快速与节能的矛盾处理。

因此，市域快线节能坡优化问题可以概括为：对以较高速度运行、较长区间里程、多种停站模式结合的线路进行节能坡设计，使线路列车在满足运行时间的同时实现能耗节省。

2 模型建立

市域快线列车运行过程受力与地铁列车基本相同。列车运行过程中主要受力有牵引力和运行阻力，其中运行阻力包括基本运行阻力、曲线附加阻力及坡道附加阻力等。本部分在相关列车动力学[9]研究的基础上，构建能耗表达函数，并建立节能坡设计优化模型。

2.1 列车运行能耗表达函数构建

为了满足不同站间距运行时间的要求，本文研究的列车区间运行操纵策略有2种，分别为牵引惰行交替模式与巡航模式。交替模式下，列车运行过程可以分为列车启动、牵引加速出站、区间牵引运行、撤除牵引惰行、制动减速进站5种运行工况，如图1(a)。巡航模式下，列车的运行过程可以分为列车启动、牵引加速出站、区间巡航运行、制动减速进站4种运行工况，如图1(b)。对应不同工况分别进行能耗分析，并根据各车站间各部分工况能耗分析求和得到列车在线路上运行的总能耗。

为了便于运行能耗的表达与计算，规定车站1和车站2之间由x个等间隔里程构成，并认为在∆内，牵引力和制动力不发生变化。本文中∆为50 m。

2.1.1 列车交替运行模式下的能耗计算

1) 列车启动能耗

启动牵引力做功表示为：

式中：0为列车启动瞬时最大牵引力；∆为单位运行长度；为列车重量为。

(a) 交替模式工况；(b) 巡航模式工况

图1 列车运行工况示意图

Fig. 1 Schematic diagram of train operating state

2) 列车牵引加速工况下的牵引能耗

已知列车瞬时启动后速度为1，1的计算可以由式(2)表示：

牵引能耗表示为：

并可计算得出第个∆内列车运行时间t

3) 列车区间运行能耗

故列车区间牵引能耗可表示为：

1和2为0-1变量，分别表示是否为牵引工况、是否为惰行工况。

4) 列车制动工况下的能耗

此里程间隔内的制动能耗表示为：

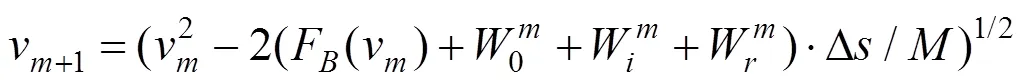
依次计算可以得出制动过程各个里程间隔的制动能耗。当列车达到最后一个里程间隔Δ时，列车的制动能耗为：

5) 列车交替模式下的区间总能耗

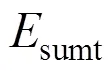
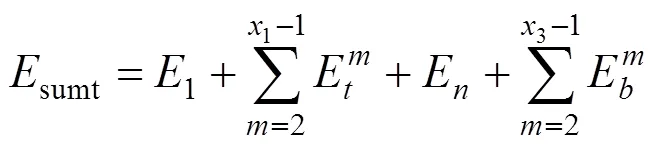
1为列车牵引加速出站过程中Δ的数量，3为列车制动减速进站过程中Δ的数量。

6) 列车全线总能耗

2.1.2 列车巡航模式下的能耗计算

列车巡航模式下，列车启动到一定速度v后以该速度匀速运行，此时，动力等于阻力，因此牵引力的做功可以用阻力做功之和的形式来表示以建立与线路条件之间的关系：

因此，巡航模式下，列车区间运行能耗可表 示为：

2.1.3 快慢车全线运行总能耗表达函数

(a) 快车跨站；(b) 慢车停车

一般认为，在规范设计标准内，坡度越大对于进出站的列车节能效果越显著，对于跨站的列车节能效果越不明显，所以快车与慢车对于小站节能坡设计的要求是相悖的，为了探究不同快慢车比例下的节能坡方案与效果，将快慢车比例加入全线能耗计算。

交替模式下，快慢车全线运行总能耗可以表示为：

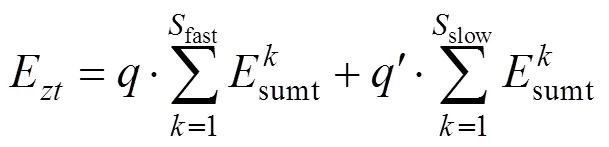
巡航模式下，快慢车全线运行总能耗可以表示为：

式中：和′分别表示快慢车比例系数。

2.2 节能坡优化模型

2.2.1 目标函数

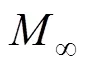
同理，巡航模式下节能坡优化的目标函数可以表示为：

式中：t为时间偏离比例。

2.2.2 节能坡优化约束条件

1) 站坪长度约束

根据线路及列车基本数据及相关研究[11]，设置站坪长度为2S=200 m，车站的中心桩号为K。即区间上的第1个坡段(车站的出站坡)的起始位置与最后一个坡段(车站+1的进站坡)的终止位置，分别固定在K+100和K+1−100处。

2) 坡长约束

根据《市域快速轨道交通设计规范》[12]，坡段长度应大于坡段最小值min且相邻竖曲线不重叠。同时为减小工程，满足线路能力，坡段长度不应大于坡段最大值max；综合以上条件确定坡长约束：

结合节能坡设计原则及《市域快速轨道交通设计规范》，对快慢车组合运行的车站进、出站节能坡坡长限制在一定的长度范围，形成坡长约束 如下：

3) 坡度约束

根据设计规范及排水要求，纵断面坡度最小值min应为1，根据地铁设计规范规定，城市轨道交通线路正线的最大坡度max不宜大于30，困难地段可采用35。故坡度约束为：

4) 列车运行约束

3 改进遗传算法

上述节能坡优化模型是非线性混合整数规划问题，精确求解算法难以求得全局最优解。因此，本研究通过改进遗传算法来实现求解。遗传算法由于其高效的全局搜索能力与极大的灵活性的优点被广泛应用。对算法中染色体编码、初始解生成、适应度函数、变异与交叉算法等进行调整，使之适应模型的结构。

算法的具体步骤如下。

3.1 编码设计

选择便于大空间搜索且精度高的实数编码方式对问题进行编码操作。实数编码分别对坡长和高程进行表示。其中染色体编码第一行为坡长编码，第二行为相邻坡段高程差编码，即前后2个变坡点高度差，在运算中，变坡点位置使用坡长累加值表示，坡度用高程差除以坡长表示。染色体具体编码形式可见图3。

图3 染色体编码图

3.2 种群初始化

种群初始化过程中首先随机产生初始纵断面设计方案。初始解不规定变坡点的数量，使用坡长的长度约束来限定变坡点数量，以10 km的区间为例，坡长的约束为500 m至2 000 m，则变坡点数量的范围区间为4至19个。

初始解生成思路为，随机生成满足约束的坡长与高程差，构建出一个基因片段，区间剩余长度与高程差减去该基因片段的坡长与高程差，直至区间剩余长度与高程差符合区间要求时停止。经过这种处理，产生了一组坡长、高程差，具有很强随机性的初始解，可以有效提升算法求解质量。

3.3 适应度函数

适应度函数值是种群进化过程中唯一的选择依据，是对每个可行解质量的一种度量，一般根据优化模型的目标函数计算可行解的适应度值。本算法中适应度函数为运行总能耗的倒数：

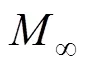
3.4 交叉

由于不同染色体的基因片段对应的变坡点里程不同，无法采用单点交叉或者多点交叉，考虑到这种情况，交叉算子采用三维空间算术交叉，将2条染色体进行空间上的交叉，若符合约束条件，则交叉成功。交叉后的子染色体′由进行交叉的双亲染色体1和2组合交叉而成，具体公式如下：

式中：1=0.5+；2=0.5−，为[0,1]的随机数。

为了提升交叉成功率，若交叉的染色体不符合约束条件，则进行混合交叉，并改变直至符合约束条件。混合交叉公式如下：

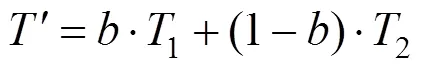
3.5 变异

变异算子采用多点变异方法，即染色体上任意片段都可以变异，增强变异能力，提升求解全局最优解能力。为了提升搜索有效解的效率，变异调整使用正态分布处理，即变异幅度越大，可能性越小。若变异后的基因片段符合约束，则变异继续，若不符合约束，则变异停止。变异公式如下：

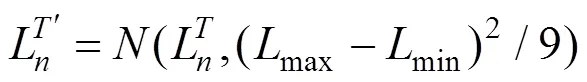
3.6 终止

当问题收敛于最优解时，算法自动停止。为了确保结果的稳定，当进化达到最大进化代数时，进化终止。

4 案例验证

选取广州地铁18号线作为案例，结合实际线路条件、运营资料等基本数据，对优化模型求解中需要采用的参数系数进行统一设置。

4.1 线路基本情况

广州地铁18号线是是国内首批可以实现地铁服务水平的全地下市域快线之一，线路大致呈南北走向，全长60 km。列车参数见表1。列车实际运行模式为巡航模式，为验证方法的有效性，本文求解中采用交替与巡航2种列车运行模式。

4.2 实验结果

算法中参数取值如下：初始种群大小为20，交叉概率为0.65，变异概率为0.01，最大迭代次数为1 000。从图4可以看出，最大适应度在320代降低到90后，趋于稳定，因此认为最大迭代数1 000可以满足优化目标的要求，且算法收敛性较好。

表1 列车参数

图4 适应度变化曲线

单位：m

各个区间人工设计方案见图5，第1行数字表示坡度，第2行数字表示坡长。考虑线路实际运营快慢车比例快车为37对，慢车为81对，接近1:2，故本节选取快慢车比例为1:2的线路设计方案作为展示，节能坡线路方案见图6。

表2为快慢车比例为1:2的情况下，交替模式节能坡优化方案与人工设计方案运行能耗结果对比。本文能耗计算均采用自主开发的列车能耗计算软件。

单位：m

表2 优化方案与人工设计方案结果对比

通过表2数据分析发现，在满足线路纵断面设计规范和运行工况约束条件下，通过遗传优化算法得到的最优解在运行能耗上较原人工设计方案单向动车运行节能效果较为明显，而运行时间偏差较小。

4.3 灵敏度分析

为了探究快慢车组合运营对于节能坡设计的影响，对不同快慢车运行比例、不同操纵模式下的节能坡方案进行优化求解并对节能效果进行比较。

4.3.1 交替模式运行能耗

由图7可知，在不同快慢车比例的情况下，慢车与快车能耗都有很大程度的减少，减少最低13.8%，最高达到21.4%。随着快车比例的增加和慢车比例的减少，慢车能耗增加，这是由于算法求解过程中更加侧重于对快车的能耗优化所导致。但是在随比例变化的过程中，慢车能耗变化幅度高于快车能耗变化幅度，因此认为，在快慢车组合运行条件下，慢车的节能效果比快车更明显。

图7 交替模式不同快慢车比例人工设计方案能耗与优化方案对比图

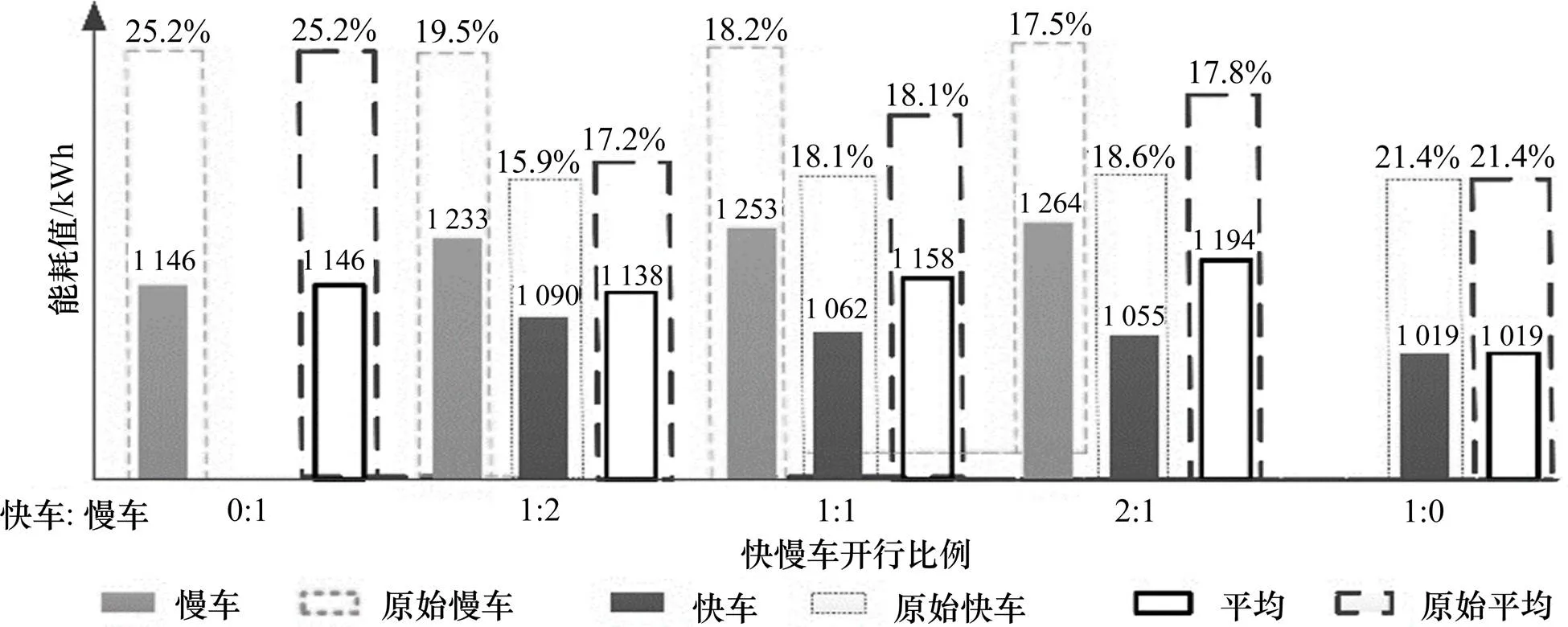
图8 巡航模式不同快慢车比例人工设计方案能耗与优化方案对比图

4.3.2 巡航模式运行能耗

巡航模式下，在不同快慢车比例的情况下，能耗减少比例都高于15.9%，说明本文提出的快慢车组合条件下节能坡设计优化模型及优化算法在2种不同运行模式下都能有效减少列车运行能耗，从而减少运营支出。不同比例下快车与慢车巡航模式能耗结果证明，慢车的节能效果比快车更明显。

5 结论

1) 针对市域快线快慢车组合运行的特点，对线路节能坡优化问题进行定义，建立列车全线运行能耗和运行时间偏差的多目标优化模型，并设计基于改进遗传算法的快速求解算法。以广州地铁18号线作为实证。结果表明本文所提模型与算法能够高效求解节能坡方案，相对于原始方案，能耗降低了15.2%~25.2%，运行时间偏差低于2%，节能效果显著且保证运行时效，具有可应用性。

2) 通过对仿真实验结果的分析，认为交替模式与巡航模式下不同的快慢车比例对节能坡设计方案和节能效果有影响，慢车比例越大，节能坡方案的总能耗减少效果越显著。

[1] 李忍相, 冯爱军, 万学红. 北京市域快线主要技术指标研究[J]. 都市快轨交通, 2014, 27(3): 27−30. LI Renxiang, FENG Aijun, WAN Xuechong. Main technical indicators of Beijing regional express railway[J]. Urban Rapid Rail Transit, 2014, 27(3): 27−30.

[2] Kim D N, Schonfeld P. Benefits of dipped vertical alignments for rail transit routes[J]. Journal of Transportation Engineering-asce, 1997, 123(1): 20−27.

[3] CHENG W C, Schonfeld P. A method for optimizing the phased development of rail transit lines[J]. Urban Rail Transit, 2015, 1(4): 227−237.

[4] LAI X, Schonfeld P. Optimization of rail transit alignments considering vehicle dynamics[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012(2275): 77− 87.

[5] 吕希奎, 李永发, 孙培培. 高速铁路进站节能坡设计方法研究[J]. 铁道标准设计, 2016, 60(9): 42−48. LÜ Xikui, LI Yongfa, SUN Peipei. Study on design of energy-saving slope in high-speed railway station[J]. Railway Standard Design, 2016, 60(9): 42−48.

[6] 陈进杰, 吕希奎. 高速铁路区间节能坡设计方法研究[J]. 铁道学报, 2013, 35(12): 83−89. CHEN Jinjie, LÜ Xikui. Research on method of energy saving gradient design for high-speed railway sections[J]. Journal of the China Railway Society, 2013, 35(12): 83−89.

[7] Kim J H, Shin Y. Formulation and evaluation of railway optimal alignment design model[J]. Journal of the Korean Society of Civil Engineers, 2014, 34(6): 1845− 1850.

[8] Kim M, Schonfeld P, Kim E, et al. Comparison of vertical alignments for rail transit[J]. Journal of Transportation Engineering-asce, 2013, 139(2): 230−238.

[9] 张东欣. 列车牵引计算仿真系统的研究与开发[D]. 北京: 北京交通大学, 2016. ZHANG Dongxin, Research and development of the traction calculation simulation system for the rail train[D]. Beijing: Beijing Jiaotong University, 2016.

[10] 刘海东, 毛保华, 丁勇, 等. 城市轨道交通列车节能问题及方案研究[J]. 交通运输系统工程与信息, 2007, 7(5): 68−73. LIU Haidong, MAO Baohua, DING Yong, et al. Train energy-saving scheme with evaluation in urban mass transit systems[J]. Journal of Transportation Systems Engineering and Information Technology, 2007, 7(5): 68−73.

[11] 乐建迪. 地铁正线节能坡设计探讨[J]. 铁道标准设计, 2008(8): 17−19. LE Jiandi Discussion on the design of energy-saving slope for the subway main line[J]. Railway Standard Design, 2008(8): 17−19.

[12] TCCES2—2017, 市域快速轨道交通设计规范[S]. TCCES2—2017, Code for design of metropolitan rapid rail transit system[S].

Research on energy saving slope optimization model and algorithm of intercity railway under multiple-train line

CAO Jinmin, LI Dewei, DONG Xinlei, YU Jie

(School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China)

Most existing researches are limited to the optimization of energy saving slope of subway under the condition of stopping trains at each station. In order to solve the problem of energy saving slope optimization of urban rail transit express line of the sprinter and express combined operation trains, based on the stress analysis of the train, this paper proposed an energy consumption function of the sprinter and express combined operation trains and established the optimization model with the minimum operating energy consumption and the minimum deviation of the train running time. Then, according to the improved genetic algorithm, a solving algorithm was designed. Finally, the operation of Guangzhou express line 18 was applied as numerical examples to validate the performance of the proposed approach. Results show that the proposed approach can effectively solve the energy saving slope design problem. Compared with the original project, the optimization approach can reduce the energy consumption of train operation by 15.2%~25.2% while maintaining the small fluctuation of running time. This paper also finds that the different proportions of sprinter and express trains have effects on the energy-saving slope design scheme and energy saving effect. The greater the proportion of sprinter trains, the higher the energy-saving proportion of the total energy consumption is.

intercity railway; energy saving slope; genetic algorithm; combined operation of sprinter and express train

U212.34

A

1672 − 7029(2020)03 − 0756 − 09

10.19713/j.cnki.43−1423/u.T20190574

2019−06−26

科技部重点研发计划资助项目(2018YFB1201402)

李得伟(1982−)，男，青海乐都人，教授，博士，从事交通运输规划与管理研究；E−mail：lidw@bjtu.edu.cn

(编辑 蒋学东)