固定支承式悬浮隧道在洋流涡激作用下的动力响应研究
范泽旭,袁勇,何任飞,张金伟,贺维国
固定支承式悬浮隧道在洋流涡激作用下的动力响应研究
范泽旭1,袁勇1,何任飞1,张金伟2,贺维国2
(1. 同济大学 土木工程学院,上海 200092;2. 中铁第六勘察设计院集团有限公司,天津 300308)
以某拟建跨海铁路隧道工程为背景,研究单跨悬浮隧道在洋流涡激作用下的共振响应问题。将隧道结构简化为两端简支的欧拉-伯努利梁,流体阻尼力和拖曳力采用Morison公式计算,采用一种基于Vanderpol方程的尾流振子模型表述尾流涡街和结构的耦合作用。通过振型分解法和龙格-库塔法对偏微分方程组进行计算,分析结果表明:在某一洋流速度范围下,考虑流固耦合效应及非线性特征对结构涡激动力响应结果有显著影响。改变悬浮隧道单跨长是解决结构涡激共振问题最为有效的办法,在某些情况下,改变结构截面尺寸及结构阻尼比也能在一定程度下控制共振响应幅度。
悬浮隧道;Morison公式;尾流振子;流固耦合;振型分解法;龙格-库塔方法

悬浮隧道(Submerged Floating Tunnel),是一种用于跨越复杂水体环境的新型交通构筑物。由于其具有对自然环境影响小、预制程度高、适用范围广等一系列优点,近年来不断受到各国研究者的关注。相比处在岩土介质中的隧道结构,悬浮隧道管段直接处于水体环境之中,利用水的作用力、自身重力以及锚索或桩台约束力的共同作用使其达到动态平衡状态。隧道变形后受到的抗力很小,易产生较大的位移响应。流体绕流隧道后,在结构后方发生边界层分离和漩涡脱落,使结构受到周期性激励力,当涡激力的频率接近结构的固有频率时,隧道结构会产生显著的动力响应,这种现象称涡激共振(VIV)。VIV发生时结构和流体之间存在相互作用,表现出明显的流固耦合特征。且由于此时结构的位移响应较大,应采用非线性方法进行分析。国内外悬浮隧道VIV的研究已取得一定进展。Remseth等[1]通过SPECTRUM程序对波浪下隧道的流固耦合特性进行研究。麦继婷[2]对波流共同作用下悬浮隧道的动力响应问题进行研究,其中水流荷载采用Morison公式进行计算。秦银钢[3]在此基础上,在管体振动方程中引入非线性因素,对洋流涡激作用下隧道的动力响应进行了更深入的讨论。然而,目前针对洋流涡激作用下悬浮隧道动力响应问题的研究还存在一些不足:采用数值模拟方法可以考虑流固耦合效应,但计算量大,在对隧道结构进行初步选型设计时效率较低。采用解析方法时,由于对涡激现象的研究还不够深入,目前大部分研究者在分析中通常还将涡激力作为简谐力考虑,其幅值根据由大量实验得到的无量纲系数计算,这种方法比较直观,但不能描述涡激作用的流固耦合特性。为描述耦合特征,可采用将流场和结构视作一整个振动系统,将尾流视为非线性振子,流固耦合通过该振子和结构之间的相互作用实现。尾流振子的概念首先由Birkhoff提出[4],Bishop等[5]通过开展大量的模型试验,验证了该方法的合理性。本文采用Facchinetti等[6]提出的一种基于Vanderpol方程的尾流振子模型。首先建立考虑非线性因素的管段振动微分方程,并以与之耦合的尾流振子方程以表述涡激力的作用。通过求解偏微分方程组,得到单跨悬浮隧道在考虑流固耦合效应下的涡激共振特征,并分析不同设计参数对结构动力响应的影响,提出在涡激作用下控制隧道动力响应的措施。
1 洋流涡激耦合振动分析方法
1.1 隧道振动微分方程的建立
在建立隧道的动力方程之前,本文作如下假设和简化:
1) 悬浮隧道属于细长柔性结构,分析时将其视为欧拉−伯努利梁,不考虑剪切变形;
2) 本文研究单跨结构,分析中可将两端边界条件视为铰接[2-3]。考虑隧道两端搁置在水中墩台的支座上,而目前使用的桥梁支座绝大部分不传递弯矩,故这样的简化是合理的;
3) 假设悬浮隧道的截面形状、材料性质沿轴线方向处处相同;
4) 假设洋流方向垂直于隧道轴线,洋流速度沿轴线均匀分布。
根据结构动力学的相关知识,两端简支梁的振动微分方程为:

式中:为抗弯刚度;为隧道线密度;()为流体作用力;为单位长度阻尼系数。
在式(1)中引入变形的非线性因素,本文中主要考虑由轴力引起的跨中二阶弯矩。设隧道的轴力沿长度方向保持不变,其大小可由下式计算[7]

式中:为材料弹性模量;为隧道横截面积;为隧道长度;为隧道轴向格林应变。
将式(2)代入式(1),考虑内力的微分关系后得到考虑非线性因素的管体振动方程:


1.2 洋流作用力的计算
式(3)中的()为结构单位长度受到的流体作用力之和,目前在海洋工程中,通常使用Morison公式计算流体力[8]。这是一种基于绕流理论的半经验半理论方法,将流体力分为拖曳力和阻尼力2项,其形式如下:

式中:F为流体拖曳力;C为附加质量系数,对于圆形截面一般取为1;′为流体密度;为隧道结构特征长度;为结构振动的加速度。

式中:F为流体阻尼力;C为阻尼系数,对于圆形截面一般取为2;为结构振动的速度。
涡激力在顺流方向和横流方向均有分量,且2个方向的振动存在耦合。但实际上横流向的涡激力要比顺流向的力大很多,这种差异通常会达到一个数量级以上。因此,为简化分析的需要,本文对涡激作用力的研究限于该力的横向分量,其表达形式如下:


采用Facchinetti在总结前人实验结果后建议的形式,振子的振动微分方程表述如下[6]:

式中:w为尾流漩涡脱落频率;和Λ为由试验得到的经验常数,根据Stansby和Blevins的实验结 果[9−10],一般取为=0.3,Λ =12。
而漩涡脱落的理论频率按照下式计算:

式中:为Strouhal数;为洋流速度;为隧道结构直径
1.3 结构涡激动力响应方程的求解
定义结构等效质量为:

将式(4)~(6)代入式(3)中,并考虑结构自身的阻尼系数为,可得到流固耦合下隧道结构的振动微分方程:


式(7)和式(10)即为流固耦合系统的总动力微分方程组。结构和尾流振子的动力耦合效应以式(7)右端的加速度项计入,当不考虑耦合作用时则忽略该项,使方程组解耦,此时尾流振子在不受外界干扰的条件下自振,其振动特征和简谐函数相同,式(10)中等号右侧的涡激激振力项退化为以往很多文献中采用的简谐作用力形式。
结构的横向位移是隧道纵向坐标和时间的函数,考虑到单跨隧道的边界条件,将其按三角级数分解为如下形式:

将式(11)代入式(10)中得:


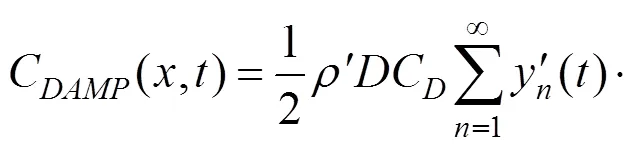

C(,)为考虑格林应变的非线性项,其形式如下:


采用伽辽金方法处理该微分方程,对得到的方程组整理后可得:

(15)
式(15)已将结构的振动化为关于时间的单变量函数。同样,将式(11)代入式(7)中,和结构振动微分方程的处理不同,对于尾流振子,考虑到在涡激作用下,结构的1阶自振模态响应较大,高阶振型由于频率较高发生共振的可能性较小,所以只考虑结构1阶振动和尾流振子的相互耦合。振子动力的方程式(7)有如下形式:
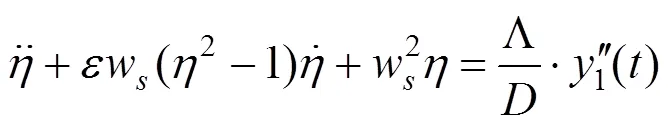
由于C(,)无法解耦,方程无法直接求得解析解,本文采用5阶4级Runge-Kutta-Felhberg算法对方程(15)及方程(16)进行数值求解[11],同时考虑到结构的高阶振型对总振动的贡献几乎可以忽 略[2-3],故只取前3阶振型加以计算。
2 算例计算与结果分析
2.1 计算参数的选择
由于目前世界上尚无在建或建成的悬浮隧道工程,本文中除基本跨长以外的其他隧道参数来自浙江舟山拟建铁路水下隧道段初步设计中的相关数据,具体如表1所示。

表1 悬浮隧道基本参数

此外,由于本文的研究并不局限于某一确定流速下结构的响应特征,表1中没有明确给出分析中使用的洋流流速。由于不同参数条件下结构共振响应对应的绝对流速不同,本文采用约化速度U代替绝对速度。其与结构固有频率有关,经计算,在0~14的约化速度范围内能够捕捉到不同情况下结构的首阶共振响应,其表达式如下所示:
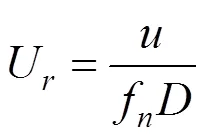
最后,悬浮隧道根据表1所给出尺寸参数确定的截面特征如图1所示。
单位:mm
图1 悬浮隧道截面示意图
Fig. 1 Cross section of SFT
2.2 计算分析结果
2.2.1 流固耦合效应对结构动力响应的影响
经过大量模型实验的验证,尾流振子模型可以较好地描述流场和处在其中结构物之间的耦合运动关系。本文采用表1中的相关参数,在较广的速度范围计算结构的动力响应峰值,得到的结果如图2所示。从图2中可知在约化速度U=4.8时流固耦合因素对共振响应的影响程度最大。图3分别描述了在该流速下隧道结构和尾流振子的振动时程 响应。
从图2中可以得到的结论有:
1) 在约化速度U<2的情况下,考虑流固耦合因素对结构动力响应的影响几乎可以忽略,这是由于此时结构的振幅、加速度等动力参数很小,尾流振子的耦合项几乎等于0,因此耦合系统表现出和非耦合系统类似的动力特征。
2) 在约化速度较高的情况下,考虑耦合后结构出现了更宽的共振响应区域,在峰值附近的曲线平滑,展现出明显的“频率锁定”效应。Carberry 等[12]在进行圆柱绕流模型试验后,认为锁定现象对应的约化速度范围为4.5~7,这和本文的结果比较接近。
3) 在非耦合曲线的位移响应达到峰值后,耦合曲线的响应仍迅速上升,在约化速度约等于非耦合情况下2倍时达到峰值。此时,2条曲线对应的位移响应相差近10倍,这说明在共振响应区域下不考虑流固耦合得到的结果是偏于危险的。
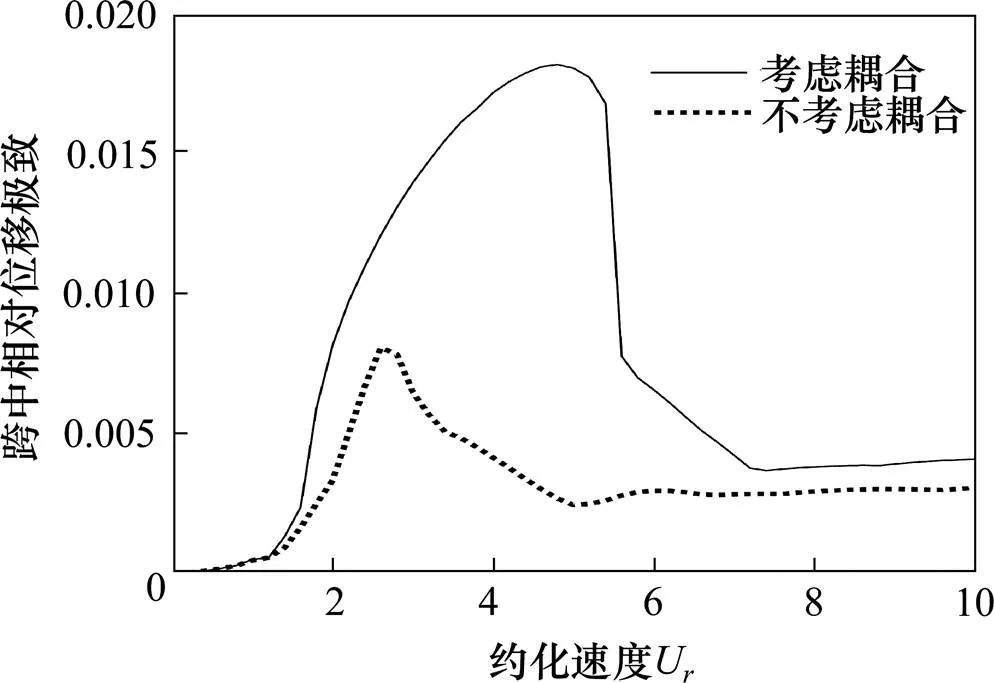
图2 流固耦合因素对动力响应峰值的影响

(a) 考虑耦合;(b) 不考虑耦合
此外,图3所示的时程响应曲线还表明流固耦合效应对结构和振子的运动有如下影响:
1) 在考虑耦合作用因素下,系统稳态振动时频率降低,最终值介于涡脱频率w和结构在水中的固有频率w。而不考虑耦合作用因素下,系统振动的稳定频率为w,即和涡激激励力的频率相同;
2) 不考虑流固耦合作用的情况下,结构和尾流振子的相位差完全取决于=0时刻两者的相位差,在本节的初始条件下,两者是反相的。而在考虑耦合因素后,两者的相位差有所降低,这也是流固耦合下振子和结构振动能够相互增强的原因之一。
2.2.2 非线性因素对结构动力响应的影响
在本文的计算中,采用格林应变计算出结构因变形而产生的轴向力,考虑大跨度梁的2次弯矩效应。图4(a)为在很大的速度范围内考虑与不考虑非线性因素2种情况下的最大位移响应,可以看到考虑非线性回复力后,响应曲线的峰值延后,且在原有的峰值后方还保持一定程度的增长趋势,直到U=8时2条曲线重合。图4(b)则说明,方程(3)中轴力项充当了非线性回复力的作用,提高了结构的实际刚度,使得振动频率有所增加。
2.2.3 单跨长度对结构动力响应的影响
从结果可以看出,不同跨长结构共振响应区域的宽度基本相同,但各曲线峰值差异较大。跨长短的工况跨中位移响应极值反而越高,需注意由于约化速度U和结构的1阶自振频率成正比,图5中各跨曲线峰值对应的水流绝对流速差异较大,直接比较同一横坐标下各曲线的值并无具体意义。涡激强度和流速平方成正比,小跨度结构共振需要很高的流速,此时涡街携带能量很高,结构的动力响应极值因此较高。同时从图中还可以看出,只要在设计悬浮隧道单跨长时避开当地洋流速度对应的共振区间,就可以有效避免由于涡激共振响应较大而可能发生的结构破坏。
2.2.4 截面尺寸对结构动力响应的影响
在明确悬浮隧道的使用要求后,内部使用限界也能随之确定,隧道的直径此时主要取决于结构的截面厚度。增大厚度,不但增加了截面的刚度,也增大了结构的迎水面积,使其承受的涡激作用力增大,因此管壁厚度对于结构动力响应影响的机理是比较复杂的,根据舟山海底隧道的设计参数,选取跨长为150 m,内径为4 m,厚度为0.05~0.20倍内径的4种工况,在较大的速度范围内研究各工况的相对位移响应。

(a) 峰值响应谱;(b) Ur=4.8时程响应结果

图5 不同跨长对动力响应峰值的影响

图6 不同壁厚对动力响应峰值的影响
从图6中可以发现,增加截面厚度和降低跨长虽然都起到了增加结构刚度的作用,但厚度的增加使得共振响应区域变窄,且速度逐渐增加时各条曲线的分岔出现得较晚。
和降低跨长相同,在一定的洋流条件下,增大截面厚度能够降低结构约化速度,进而限制结构振幅。但由于此时增加厚度不仅增加了截面的弹性模量,也增加了结构线密度,使得增加结构刚度的效果不如减少跨长的方法明显。
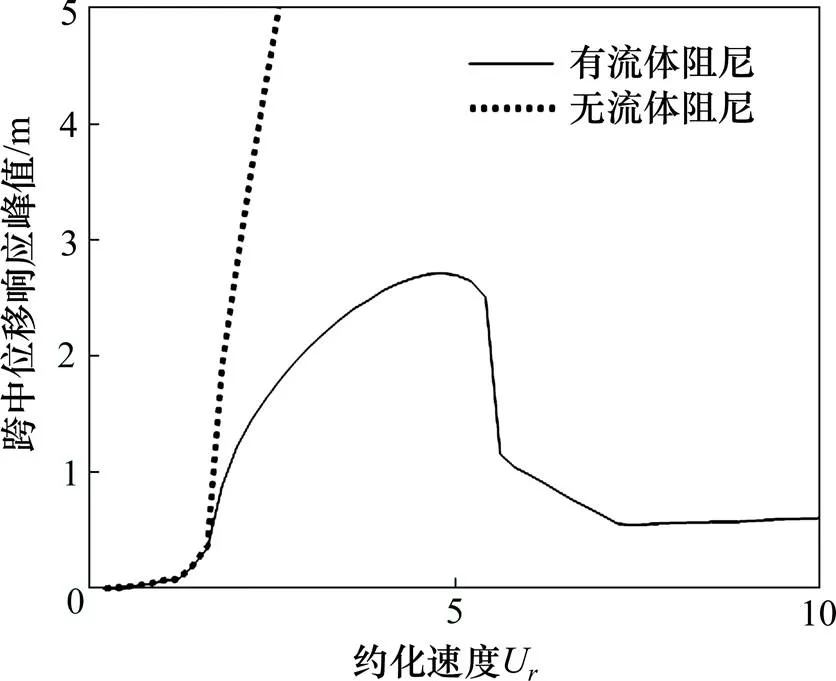
图7 流体阻尼对动力响应峰值的影响
2.2.5 阻尼大小对结构动力响应的影响
由于悬浮隧道处于流体介质中,在研究其动力特性时不仅考虑附加质量,还要考虑流体阻尼的影响。流体阻尼大小同结构在介质中的相对运动速度成正比,因此不同情况下对稳态振动的影响程度也是不同的。图7表明在洋流速度较低时,流体阻尼的作用尚不明显,但当流速继续增加时,流体阻尼对结构动力响应的影响十分显著。
事实上,在工程中很难直接调整流体阻尼的大小。图8为不同结构阻尼的动力响应曲线,从中可以看出,结构阻尼并不会改变共振响应区域的范围,但随着阻尼比的增加,结构的最大峰值振幅有所降低。在约化速度较小的情况下,增加结构阻尼对计算结果基本无影响,而在共振峰值附近使结构位移响应明显降低。

图8 结构阻尼对动力响应峰值的影响
3 结论
1) 大量试验已经证明使用尾流振子模型计算水中结构物的流固耦合运动是可行的。本文针对悬浮隧道在洋流涡激作用下动力响应的计算表明,在水流速度较低时(U<2),结构的位移响应总体较小,流固耦合的特征并不明显,此时可将涡激力看作简谐作用力,忽略耦合作用。但当水流速度较大时(U>2),考虑流固耦合效应后,结构和涡街两者的相位会发生趋近,它们之间的相互作用也不断增强,最终稳定后系统的位移响应将显著高于忽略耦合效应的情况。总的来说,在悬浮隧道的设计中考虑耦合因素对结构安全十分重要。
2) 考虑非线性特征相当于增加了结构的几何刚度,提高了稳定后系统振动的频率。在洋流速度较低时,由于结构的位移响应较小,考虑非线性因素对结构峰值位移的影响不大。但当洋流速度较高,且处在特定范围(8>U>6)时,考虑非线性因素得到的位移响应结果偏高,此时仍采用线性理论计算是偏于危险的。
3) 在研究不同设计参数对结构涡激动力响应的影响后,本文认为改变结构跨长是控制涡激共振响应最有效的措施。当悬浮隧道选址确定后,当地的平均洋流速度可以大致确定下来,在设计单跨长时应避开可能发生涡激共振的跨长区间。当洋流速度的变化范围很大,或当地地质条件不允许灵活的改变跨长时,开展合理的经济性评估后也可选择适当增加截面尺寸或增大结构自身阻尼比的方法,作为辅助控制手段。
[1] Remseth S, Leira B J, Okstad K M, et al. Dynamic response and fluid/structure interaction of submerged floating tunnels[J]. Computers & Structures, 1999, 72(4−5): 659−685.
[2] 麦继婷. 波流作用下悬浮隧道的响应研究[D]. 成都: 西南交通大学, 2005. MAI Jiting. Dynamic response of submerged floating tunnel under wave-current effect[D]. Chengdu: Southwest Jiaotong University, 2005.
[3] 秦银钢. 洋流涡激作用下水中悬浮隧道稳定性的关键技术研究[D]. 成都: 西南交通大学, 2009. QING Yingang. Major stability characteristics of submerged floating tunnel under vortex induced vibrations[D]. Chengdu: Southwest Jiaotong University, 2009.
[4] Birkhoff G. Formation of vortex streets[J]. Journal of Applied Physics, 1953, 24(1): 98−103.
[5] Bishop R E D, Hassan A Y. The lift and drag forces on a circular cylinder in a flowing fluid[J]. Proceedings of the Royal Society of London, 1964, 277(1368): 32−50.
[6] Facchinetti M L, Langre E D, Biolley F. Coupling of structure and wake oscillators in vortex-induced vibrations[J]. Journal of Fluids & Structures, 2004, 19(2): 123−140.
[7] 凌道盛. 徐兴. 非线性有限元及程序[M]. 杭州: 浙江大学出版社, 2004: 40−43. LING Daosheng. XU Xing. Nonlinear finite element method and program[M]. Hangzhou: Zhejiang University Press, 2004: 40−43.
[8] 孙意卿. 海洋工程环境条件及其荷载[M]. 上海: 上海交通大学出版社, 1989. SUN Yiqing. Environmental conditions and loads of marine engineering[M]. Shanghai: Shanghai Jiaotong University Press, 1989.
[9] Stansby P K. The locking-on of vortex shedding due to the cross-stream vibration of circular cylinders in uniform and shear flows[J]. Journal of Fluid Mechanics, 1976, 74(4): 641−665.
[10] Blevins R D. Flow-induced vibration[M]. Flow-Induced Vibration, 1977: 6.
[11] 薛定宇. 高等应用数学问题的MATLAB求解[M].北京: 清华大学出版社, 2004. XUE Dingyu. Advanced applied mathematical problem solutions with MATLAB[M]. Beijing: Qinghua University Press, 2004.
[12] Carberry J, Sheridan J, Rockwell D. Forces and wake modes of an oscillating cylinder[J]. Journal of Fluids & Structures, 2001, 15(3−4): 523−532.
Dynamic response analysis of submerged floating tunnel supported on columns in vortex-induced vibration
FAN Zexu1, YUAN Yong1, HE Renfei1, ZHANG Jinwei2, HE Weiguo2
(1. College of Civil Engineering, Tongji University, Shanghai 200092, China; 2. China Railway Liuyuan Group Co., Ltd, Tianjin 300308, China)
In the context of a planned tunnel project, this study focused on the dynamic response of single-span submerged floating tunnel (SFT) in resonance with vortex shedding. Tunnel tube was simplified as a simply supported Euler-Bernoulli beam. Drag force and damping force were calculated using Morison formula. By introducing a wake oscillator based on van der pol equation, the coupling between structure and wake could be thoroughly analyzed. Mode analysis method and Runge-Kutta method were adopted in solving differential equations. The results show that structural-wake coupling and nonlinearity have a significant influence on dynamic response of SFT. Changing span length is the most effective way in avoiding resonance problem. And under certain circumstance, the resonance response can also be restricted by optimizing sectional dimension and structural damping.
submerged floating tunnel; Morison formula; wake oscillator; structural-wake coupling; mode analysis method; Runge-Kutta method
U451.3
A
1672 − 7029(2020)03 − 0653 − 07
10.19713/j.cnki.43−1423/u.T20190471
2019−05−30
国家自然科学基金资助项目(51478343)
袁勇(1963−),男,云南景东人,教授,博士,从事地下结构动力问题研究;E−mail:yuany@tongji.edu.cn
(编辑 阳丽霞)

