基于响应面法的静电纺丝制备壳聚糖/聚氧化乙烯的工艺参数优化
赵鹏程 王俊元 梅林玉 曹一明

摘要: 為了对静电纺丝过程工艺参数进行优化,改善壳聚糖(CS)/聚氧化乙烯(PEO)纳米纤维膜的机械性能,选取CS与PEO质量配比、电压、接收距离作为优化参数,抗拉强度和伸长率作为响应性能指标,按照BoxBenhnken(BBD)设计实验,采用响应曲面分析的方法,建立相对应的预测回归模型并进行方差分析。利用残差概率图进行可靠性验证后,得出了各参数对机械性能影响的显著性及其交互作用对膜的影响。利用DesignExpert软件的Optimization模块优化后得到了各工艺参数间的最优组合:CS与PEO质量配比8︰2、电压15.5kV、接收距离9.88cm。
关键词: 静电纺丝;壳聚糖;聚氧化乙烯;参数优化;响应曲面法
中图分类号: TS102.54;TQ340.64文献标志码: A文章编号: 10017003(2020)02003104
引用页码: 021106DOI: 10.3969/j.issn.10017003.2020.02.006
Optimization of process parameters for preparation of CS/PEO by electrospinning
based on response surface methodology
ZHAO Pengcheng, WANG Junyuan, MEI Linyu, CAO Yiming
(School of Mechanical Engineering, North University of China, Taiyuan 030051, China)
Abstract: In order to optimize the process parameters of the electrospinning process and improve the mechanical properties of the CS/PEO nanofiber membrane, the mass ratio of CS and PEO, voltage and receiving distance were selected as the optimization parameters, and tensile strength and elongation were used as response performance indicators. According to the BoxBenhnken (BBD) design experiment, the response surface analysis methodology was used to establish the corresponding predictive regression model and conduct analysis of variance. After the reliability verification by the residual probability map, the significance of the influence of each parameter on the mechanical properties and the influence of the interaction on the membrane were obtained. The optimal combination of process parameters was obtained after the optimization with the Optimization module of DesignExpert software: the ratio of CS to PEO 8︰2, the voltage 15.5kV, and the receiving distance 9.88cm.
Key words: electrospinning; chitosan; polyethylene oxide; parameters optimization; response surface methodology
静电纺丝法是一种制造连续纳米纤维的方法,其工作原理是通过高压静电使溶液在喷射过程中挥发拉伸,形成纳米纤维丝[1]。纳米纤维材料的机械性能较好,能够与纳米级化学物质相结合,在药物催化、纳米传感器、生物医药等诸多领域都有着很大的发展前景,因此,纳米纤维膜在未来的各个行业一定有着不可替代的作用,研究纳米纤维膜的机械性能的意义更是不言而喻[2]。本文从静电纺丝工艺参数对纳米纤维膜的机械性能的影响入手进行分析。在静电纺制备CS/PEO纳米纤维膜的过程中,影响膜的机械性能的参数主要有CS与PEO质量配比、电压和接收距离,故选取了这三个具有代表性的工艺参数进行优化[3]。由于常用的正交实验设计的缺点是无法建立优化参数与响应目标之间的拟合方程,因此无法进一步地进行优化。响应面分析法不但实验次数少,而且求得的方程精度高,故为获得具有优良性能的膜,本文创新性地结合响应面法[47],建立回归拟合数学模型,结合利用DesignExpert软件进行后期的实验数据分析,对实验结果进行数学统计方法来优化静电纺丝技术参数,得到最优工艺参数组合[8]。
1响应面法实验
1.1试剂与材料
脱乙酰度99%、相对分子量3×105壳聚糖(CS)(上海信裕生物技术有限公司),相对分子量4×107聚氧化乙烯(PEO)(SPECTRUM CHEMICAI MFG.CORP),冰乙酸(CH3COOH)分析纯(乙酸含量≥99.5%,天津市大茂化学试剂厂),蒸馏水(H2O)分析纯(广州屈臣氏食品饮料有限公司)。
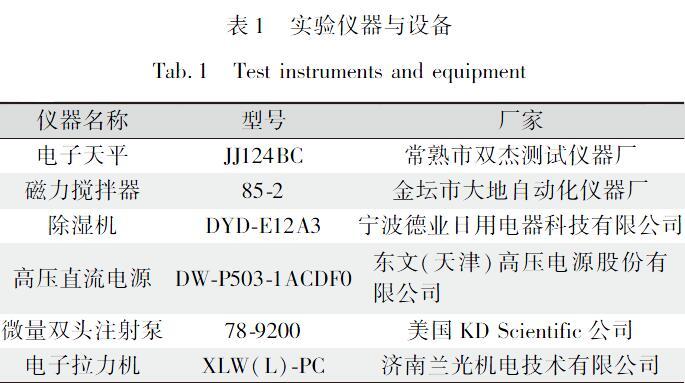
主要的仪器与设备见表1。
1.2方案设计与结果
1.2.1纤维膜的制备
选取50mL的烧杯,倒入35g左右的冰乙酸,计算配制70%冰乙酸溶剂。在25mL烧杯中加入0.14g CS,再加入006g PEO,共计0.2g;最后加前面配置好的溶剂至20g,即溶液质量分数为1%,其中CS︰PEO为7︰3。用玻璃棒搅拌至肉眼看不到溶质后,放在磁力搅拌机上继续搅拌3h。同理配出CS与PEO比例为8︰2和9︰1,质量分数为1%的溶液。
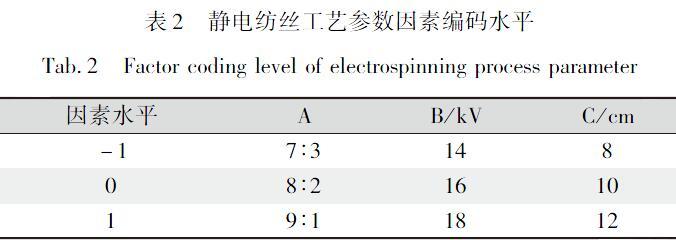
溶液性质、电压和接收距离是静电纺丝工艺中最重要的参数,由于CS与PEO的配比、电压及接收距离对膜的影响较大,所以将适用于静电纺丝工艺范围的工艺参数CS与PEO质量配比、电压和接收距离作为优化变量,将评价膜的机械性能的主要参数抗拉强度和伸长率作为响应性能指标。本实验采用BoxBenhnken(BBD)划分优化参数的水平,响应面实验法中常用的有CCD(Central Composite Design)和BBD两种方法,其中BBD法可以用比CCD法更少的实验次数获得足够多的实验数据和误差信息。再根据之前做过的单因素实验找到优化参数的浮动范围,并把这个范围划分为3个因素水平,编码如表2所示。将溶液放入针管内,按照表2调整微量双头注射泵和高压电源参数,调整接受装置距离进行静电纺丝法制备纳米纤维膜[9]。每张膜纺2h,待收集器上成膜后,关闭高压直流电源,自然条件下晾干,用刀片小心揭膜,取下制得的CS/PEO纳米纤维包装膜。将上述静电纺丝制得的CS/PEO纳米纤维包装膜裁剪成10cm×15cm的形状,置于干燥箱内干燥24h。
1.2.2机械性能测试
参照ASTM D638《塑料拉伸性能测定方法》,通过电子拉力试验机测试,得到膜的抗拉强度和延伸率。电子拉力试验机测定时的数据为拉伸载荷98N,拉伸速度25mm/min。记录膜破裂时的拉力和伸长的距离。试样裁剪成3cm×5cm规格的长条,每个试样测5次,取平均值。抗拉强度按下式计算:
TS=Fb×d(1)
式中:TS为抗拉强度,Mpa;F为试样断裂时承受的最大张力,N;b为试样宽度,mm;d为试样厚度,mm。
断裂伸长率按下式计算:
E/%=L1-L0L0×100(2)
式中:E为试样断裂伸长率,%;L0为试样原始标线间的距离,mm;L1为试样断裂时标线间的距离,mm。
按照BBD的响应面法设计出最优实验,根据上述已经划分的静电纺丝参数的编码因素组合进行17组实验,获得抗拉强度和伸长率的数据,实验方案与结果如表3所示。
2静电纺丝工艺参数数学模型的建立与可靠性检验
2.1静电纺丝工艺参数数学模型的建立与优化
建立回归模型可以对工艺参数进行优化,对响应指标进行预测,故为得到最优回归拟合方程,利用DesignExpert软件,对静电纺丝实验所得到的抗拉强度和伸长率结果进行多元回归方差分析,分别得到了两种响应指标的数学回归模型,见表4、表5。其中P值用于分析对象显著性,P<0.0001表示响应模型达到了极显著的水平,P<0.05表示响应模型达到了较为显著的水平,P>0.1表示响应模型不显著[10]。
由表4可知,A、A2、B2对于抗拉强度的P值小于00001,说明它们对抗拉强度的影响极为显著;B、C、C2的P值小于0.05,说明它们对抗拉强度的影响较为显著;其余因素的P值均大于0.1,说明它们对抗拉强度的影响不显著;比较均方值的大小可知,影响抗拉强度的工艺参数前后排序为A>B>C;交互融合作用的前后顺序为AB>BC>AC。由表5可知,B、C、AB、AC、BC、A2、B2、C2的P值小于0.05,说明它们对伸长率的影响较为显著;其余因素的P值均大于0.1,说明它们对伸长率的影响不显著;比較均方值的大小可知,影响伸长率的工艺参数前后排序为B>C>A;交互融合作用前后顺序为BC>AB>AC。最后根据响应面法建立的回归数模型为:
R1=20.64-1.19A-0.81B+0.47C-0.42AB-0.05AC-0.25BC-6.38A2-2.33B2-0.91C2(3)
R2=66.44+3.45A-8.26B-6.51C-6.93AB+6.23AC-7.2BC-9.2A2-11.77B2-13.12C2(4)
2.2静电纺丝分析模型的可靠性检验
残差正态概率图是通过观察数据是否基本符合一个直线模式来进行可靠性检验,用以说明所建模型是否准确。由图1、图2可知,图中的数据都基本遵循了一条直线的模式,并没有出现突出变异的数据点,这说明模型的误差是在可控范围内的,建立的数学模型的准确率是可信的。
2.3基于响应曲面法的参数优化验证
2.3.1响应曲面分析
基于方差分析和回归模型的建立,表明交互融合作用对伸长率的影响较为显著。利用DesignExpert软件,得到了图3所示的电压和接收距离(BC)的响应曲面,可以看到,随着电压和接收距离的增加,伸长率逐渐增大,在到达中心点后再慢慢减小。图3中响应曲面对应的等高线曲率较大,表明电压(B)和接收距离(C)的交互融合作用对伸长率的影响是显著的。
2.3.2参数优化与验证
在DesignExpert软件中利用3D响应面法对静电纺丝工艺的响应面回归模型方程进行分析,通过Optimization的优化模块对响应指标的极值点进行自动搜索,得到了工艺参数的最优组合为:CS与PEO质量配比8︰2、电压15.5kV和接收距离9.88cm,这个参数组合下的抗拉强度20.67MPa、伸长率68%。对此结果进行检验:用此参数组合进行重复实验,得到的抗拉强度20.89MPa、伸长率65.6%。经过计算可得:预测与实验得到的抗拉强度的相对误差为1.05%,伸长率的相对误差为3.65%,误差都很小,所以响应面优化方法是比较精准的,初步说明可以应用到静电纺丝工艺当中。
3结论
通过静电纺丝实验得到了基础数据,在利用响应面中的BBD方法进行实验后,再进行数据分析,建立了以静电纺丝工艺参数为自变量的抗拉强度和伸长率的数学回归拟合模型。在实验的基础上,为一定浮动范围内的静电纺丝工艺参数提供了可参考的实验依据。然后,通过分析响应回归模型,又得出了3个工艺参数分别对抗拉强度和伸长率这两个响应指标的影响顺序。最终,获得了静电纺丝工艺的最优工艺参数组合是:CS与PEO质量配比8︰2、电压15.5kV和接收距离9.88cm。
参考文献:
[1]黄建, 刘琳, 姚菊明. 静电纺再生丝素蛋白纳米纤维膜的工艺及性能[J]. 丝绸, 2011, 48(1): 2023.
HUANG Jian, LIU Lin, YAO Juming. Technology and properties of regenerated bombyx mori silk fibroin nanofiber membrane by electrospinning method [J]. Journal of Silk, 2011, 48(1): 2023.
[2]王永鹏, 刘梦竹, 路大勇. 用静电纺丝法制备可交联高性能聚合物纳米纤维[J]. 纺织学报, 2018, 39(1): 610.WANG Yongpeng, LIU Mengzhu, LU Dayong. Preparation of crosslinkable and high performance polymers nanofibers by electrospinning [J]. Journal of Textile Research, 2018, 39(1): 610.
[3]LOU C W, WU Z H, LEE M C, et al. Highly efficient antimicrobial electrospun PVP/CS/PHMGH nanofibers membrane: preparation, antimicrobial activity and in vitro evaluations [J]. Research on Chemical Intermediates, 2018, 44(8): 49574970.
[4]MATIVENGA P T, RAJEMI M F. Calculation of optimum cutting parameters based on minimum energy footprint [J]. CIRP Annals, 2011, 60(1): 149152.
[5]MVELCHEV S, KOLEV I, IVANOV K, et al. Empirical models for specific energy consumption and optimization of cutting parameters for turning [J]. Journal of Cleaner Production, 2014, 80: 139149.
[6]范煥新, 李玲, 马超云. TiO2纳米管薄膜的制备与光学性能研究[J]. 科学技术与工程, 2012(5): 987991.
FAN Huanxin, LI Ling, MA Chaoyun. Preparation and optical properties of TiO2 nanotubes film [J]. Science Technology and Engineering, 2012(5): 987991.
[7]魏娜, 孙诚, 王丽超, 等. 静电纺羧甲基壳聚糖纳米纤维直径的预测模型[J]. 包装工程, 2016, 37(13): 813.
WEI Na, SUN Cheng, WANG Lichao, et al. Prediction model of the diameter of carboxymethyl chitosan nanofibers prepared by electrospinning [J]. Packaging Engineering, 2016, 37(13): 813.
[8]KANT G, SANGWAN K S. Prediction and optimization of machining parameters for minimizing power consumption and surface roughness in machining [J]. Journal of Cleaner Production, 2014, 83: 151164.
[9]许乐, 杨庆, 黄丽媛, 等. 壳聚糖/聚氧化乙烯静电纺丝工艺研究[J]. 合成纤维工业, 2011, 34(4): 2830.
XU Le, YANG Qing, HUANG Liyuan, et al. Study on chitosan/polyoxyethylene oxide electrospinning process [J]. China Synthetic Fiber Industry, 2011, 34(4): 2830.
[10]RAJEMI M F, MATIVENGA P T, ARAMCHAROEN A. Sustainable machining: selection of optimum turning conditions based on minimum energy considerations [J]. Journal of Cleaner Production, 2010, 18(18): 10591065.
收稿日期: 20190528; 修回日期: 20191219
基金项目: 山西省青年科技研究基金项目(2015021068)
作者简介: 赵鹏程(1995),男,硕士研究生,研究方向为生物制造、纳米材料、静电纺丝。通信作者:王俊元,教授,1183590618@qq.com。

