非金属管道微小泄漏动力学数值模拟和试验对比*
岳云飞 杨文斌 严欣明 毛小虎 郝永梅
(1.江苏省特种设备安全监督检验研究院 江苏常州 213016;2.常州大学环境与安全工程学院 江苏常州 213164)
0 引言
PE管具有较高的性价比,已被广泛应用于燃气、能源等管道工程中,但由于其焊接接头质量难以检测,导致管道发生泄漏等故障时难以及时发现。PE管泄漏检测是当前的难题,从声音传播特性来看[1],泄漏信号传播的介质是土壤、水、管材等,因介质的疏密性和声波传播距离不同,导致声音衰减系数不同,尤其是微小孔泄漏对管道的运行参数影响甚微,信号特征不突出,使得其更难以被检测并及时发现。由于流体受管道内外的压力、温度或浓度梯度影响产生迁移的现象是流体泄漏的本质,研究管内流体穿过泄漏孔处在管外环境中的流量参数变化即成为研究泄漏规律的重要部分[2]。因此,探究PE管道微小孔泄漏的规律为其泄漏检测提供理论依据十分必要。
首先,预测管道事故后果的前提和基础是明确管道的泄漏率及泄漏量。国外学者BECK等[3]提出低压环境下,单相流通过狭小裂缝的泄漏速率计算公式;HELENA等[4]率先发现并提出了管道和大孔模型的概念,并在此基础上,对管道大孔泄漏、小孔泄漏的动态稳定性进行了深度的研究与分析;YOUNG等[5]首次发现并提出了一种计算高压管道泄漏状态下的简化模型;KAM[6]通过出口流量监控判断泄漏,并建立了海底水平泄漏管道压力分布模型;CROWL等[7]假想流体在管道内流动和泄漏是在绝热的条件下且管道内部起始点压力固定,建立了关于管道完全断裂的泄漏模型。国内,潘旭海等[8]对事故泄漏的过程、机理和泄漏源形式进行了研究和分析,得出各种模式下泄漏源的强定量模型;王兆芹[9]提出了计算高压力下两种常见的管道泄漏模型:管道的大孔泄漏模型和完全破裂模型;霍春勇等[10]提出了一种新的通用模型,用于计算长距离输送管道泄漏率,还说明了如果管道处于非稳定的状态,计算得到的应是流体的平均泄漏率;蔺跃武等[11]提出了一种关于管道完全破裂后泄漏量的计算模型,建立在绝热条件下且管道内的流体为理想流体,假设管道的泄漏过程为等熵流动,可以针对不同泄漏孔径下的不同泄漏情况进行分析从而得出结果。以往的研究主要集中在小孔泄漏的计算模型上,针对PE管微小泄漏孔泄漏参数分布规律的研究甚少[12]。
因此,本文针对液体PE管道发生微小泄漏的情况,使用Fluent软件构建三维管道模型进行数值模拟及试验分析,找出泄漏孔处流体参数的分布规律,为PE管道泄漏检测和安全管理提供理论依据。
1 泄漏数值模拟的基础
1.1 PE管道的基本特征
PE(聚乙烯)管密度低且强度高、耐腐蚀、便于施工、具有良好的绝热性能,且其比传统金属管更光滑的内层表面,能够有效降低输送过程中的能量损失,增强管道的输送能力。PE管道的应用不仅为城市发展节约了经济成本,而且有效解决了物质运输过程中存在的管道腐蚀问题,延长了管道的使用寿命[13]。
1.2 基本控制方程
守恒定律是流体流动必然遵循的准则,在泄漏扩散模拟中所涉及的基本守恒定律包含动量、能量和质量守恒定律,其各自对应的控制方程即是数学描述,具体形式见文献[14-15]。标准k-ε模型是经过大量实验总结得到的半经验化公式,其中湍能k代表特征速度,湍流耗散率ε代表特征长度尺度。k方程和ε方程分别如式(1)~式(2)所示。
(1)
(2)
式中,湍能k和耗散率ε的湍流普朗特数为σk=1.0,σε=1.3;ρ为密度;μ为粘性系数;Gk和Gb分别为由层流速度梯度和浮力产生的湍流动能;C1ε,C2ε,C3ε是常量;Ym为过度扩散产生的波动;Sk,Sε为自定义;湍流速度由μi=ρcμk2/ε确定,其中cμ是常量。模型常量分别为:cμ=0.09,C1ε=1.44,C2ε=1.92。
1.3 模型构建及边界条件。1.3.1 模型与网格划分
建立模拟区域为长20 m、内径150 mm、壁厚4.5 mm的聚乙烯管道模型。在距离模型上游端口6,16 m处设置两个孔径相同的圆形泄漏孔。管道外部介质为空气,内部流体介质为具有不可压缩性的水。利用CFD软件设置非结构化的四边体单元网格后,对模拟区域进行非均匀性的网格划分。同时,采取在各泄漏孔及邻近区域加密网格的方式以保证模拟液体泄漏现象的准确性,网格划分如图1所示。

图1 模拟管道的网格划分
1.3.2边界条件设置
边界条件的设置在动力学规律数值模拟中对结果有着十分重要的作用[16]。本次模拟主要的设置情况为:入口边界条件设置为质量流量进口,入口的质量流量设置为61.85 kg/s,同时,根据模拟方案对入口处的压力进行调整;为确保流体顺利的流出,出口以及泄漏孔处边界条件为开放性压力出口,并将管道出口处和泄漏孔处压力设置为标准大气压力。此外,为提高模拟的准确性,使用Scalable函数作为近壁位置的壁面函数,并将管体的边界条件设置为绝热无滑移。
2 液体PE管道泄漏仿真
2.1 压力对管道泄漏规律的影响
构建1.3.1中所述管道模型,设置两泄漏孔径为1 mm,分别在管道入口压力为0.127,0.227和0.327 MPa 3种边界条件下进行数值模拟,比较泄漏孔径固定时,入口压力变化对流体流动参数的影响。由于结果显示两个泄漏孔处参数分布基本相同,故仅以孔1处的压力、流速分布状况来说明情况,图2、图3为泄漏孔1处的压力、流速分布矢量图。
图2、图3表明:管道发生泄漏时,主流体的流动参数几乎不受泄漏影响,管道内部的压力和流速比较稳定,主要是在泄漏孔处差异较大。管壁约束作用导致管壁附近流体的流速较低;流体流速与距泄漏孔的距离成反比,速度等值线大致呈外凸圆弧;但由于管内流体本身具有一定速度,部分流体在直接冲击泄漏孔壁面时瞬间停滞,导致泄漏孔处左右压力和流速的分布不对称。

(a)0.127 MPa (b)0.227 MPa (c)0.327 MPa
图2 不同压力下的泄漏压力分布

(a)0.127 MPa (b)0.227 MPa (c)0.327 MPa
当泄漏孔径固定时,泄漏孔处的压力、流速与管道内压力呈正相关,其中,由于流体的冲击作用,背向来流方向壁面的流速相对较低,而面向来流方向壁面附近流速最高,最大约23 m/s;当射流稳定后,泄漏孔处在卷吸作用下产生漩涡,在泄漏孔根部的边缘处和中心处分别形成了两个负压区和一个高压区,且越靠近射流核心处卷吸作用越强烈,但由于泄漏孔面积本身较小,整个泄漏孔截面几乎均为负压。
2.2 泄漏孔径对泄漏规律的影响
构建上述管道模型,将管道入口压力设置为0.2 MPa,分别对管道两泄漏孔径为1,2和5 mm的3种模型进行数值模拟,探究管内压力固定时,泄漏孔径的变化对管道内部流动参数的影响。各泄漏孔径下孔口处的压力和流速分布矢量图分别如图4、图5所示。

(a)1 mm泄漏孔径 (b)2 mm泄漏孔径 (c)5 mm泄漏孔径
图4 不同泄漏孔径下的泄漏压力分布

(a)1 mm泄漏孔径 (b)2 mm泄漏孔径 (c)5 mm泄漏孔径
液体PE管道泄漏在0.2 MPa压力条件下以各孔径泄漏时泄漏处的流量变化情况如表1所示。

表1 各泄漏孔径下管道的质量流率报告 kg/s
从表1可以看出,相同泄漏孔径下的泄漏孔1与泄漏孔2的质量流率基本相同,而泄漏孔泄漏的流量相对于入口来说较小,原因是泄漏孔径比起管径十分微小,因此不太明显,这也导致了出入口的质量流率基本相同,差距比较小。且由图4看出,流体在到达泄漏孔根部端面时由于惯性作用不能及时变向,撞击在此端面上使动能转化为压力能,形成了小范围的高压区,因而管道内最高压力稍大于0.2 MPa,从图中还可以看到泄漏量随着泄漏孔径的增大而上升。
对孔口截面与孔中心轴线交点处的流动参数进行对比,结果如图6、图7所示。
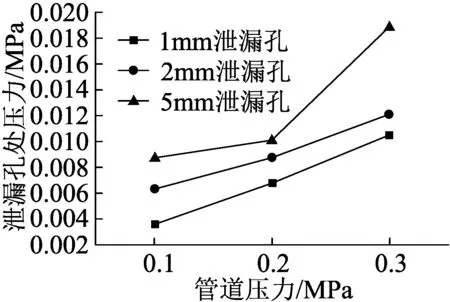
图6 不同泄漏孔处压力对比

图7 不同泄漏孔处流速对比
图4、图5显示:此种泄漏模式下孔口处压力与流速参数的分布情况与不同管道压力下的分布规律几乎一致。管道发生泄漏时,主流体受泄漏影响较小,管道内部的压力和流速比较稳定,差异主要体现在泄漏孔处;由于管壁约束作用,管壁附近流体的流速较低,流体流速与距泄漏孔的距离成反比;但由于泄漏孔处近壁面的流体在向外部泄漏时撞击到泄漏孔壁面,使得流体瞬间停滞,导致孔口左右压力和流速的分布并不对称。
图6、图7显示:当入口压力固定时,泄漏孔处高压区的内部压力值及其范围与泄漏孔径成正比,同时,低压区的范围成上升趋势但其压力随之降低;当稳定射流后,泄漏孔根部的边缘处在卷吸作用的影响下形成了两个负压区,并且两侧流体的速度有所降低;流体在其到达泄漏孔根部端面时由于惯性作用无法及时变向,撞击在此端面上使流体瞬间停止,此时动能转化为压力能形成了高压核心区,但由于孔口面积较小,整个泄漏孔截面几乎均为负压。因为1,2以及5 mm泄漏孔对于模拟管道都属于小孔泄漏且两者相差甚微,所以压力相同孔径不同时,虽然泄漏孔处的流速有所上升但波动较小,因而小孔范围内,孔径并非是影响泄漏速度的重要因素。
3 液体PE管道两孔泄漏试验
3.1 基本情况
试验管道选取长20 m、内径150 mm、壁厚4.5 mm的PE管道。管道内部流体介质为水,在距离管道上游端口6,16 m处设置两个孔径相同的圆形泄漏孔,微压力传感器的布置情况如图8所示。

图8 试验装置布置示意
3.2 压力对泄漏规律的影响试验
设置两泄漏孔径为1 mm,在管道入口压力为0.1,0.2 MPa两种情况下分别进行试验,同时加入压力0.1 MPa无泄漏发生时的状态参数,分析各压力条件下管道不同泄漏状态的压力参数变化规律。管道的两点泄漏压力电压上、下游状态分析如图9。

(a)上游变化
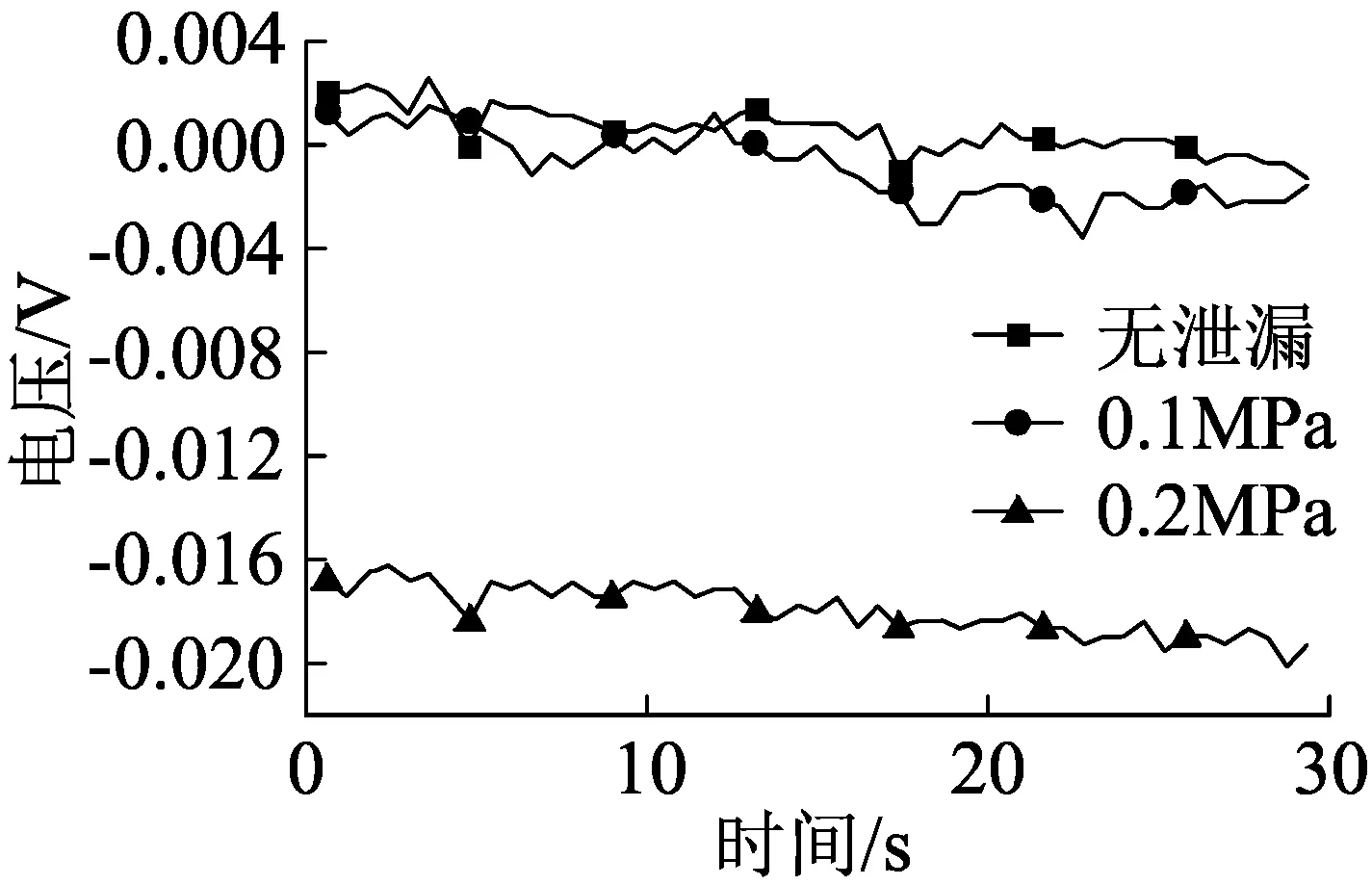
(b)下游变化
图9显示:虽然电压信号比较敏感,但其总体的变化趋势足以说明管内压力呈下降趋势,管道下游的压力基本小于其上游的压力;管内的阻力使得无泄漏管的上下游也会存在一定程度的压力降,压差即是输送过程中损失能量的体现;初始压力的增大,导致管内压力下降的速度与幅度也随之增大,这是因为管道内外较大的压差使得流体得以更快的泄漏。
3.3 泄漏孔径对泄漏规律的试验分析
在无泄漏、泄漏孔径为1,2 mm的3种情况下,管道压力为0.1 MPa,探究管道入口压力固定时,泄漏孔径大小对流动参数变化的影响,试验结果如图10。

(a)上游变化

(b)下游变化
图10显示:泄漏的发生使得管内压力逐渐降低,流体在流经管道时由于管内的阻尼而造成的能量损失可以用上下游的压差表示。与未发生泄漏时相比,压力电压的下降速度与管道泄漏孔径的大小成正相关;同时,由于1,2 mm的孔口对于该规格的管道而言都是小孔,可以推出两种孔径泄漏孔处的流速都较低,且上下游流量几乎不变,即小孔范围内孔径并非是影响泄漏流速的主要因素,这印证了数值模拟所得结论。
4 模拟与试验结果对比分析
PE管道微小孔泄漏的数值模拟与试验结果发现,泄漏孔处流速方面的结果比较相近,但在孔口处泄漏压力方面的结果存在差异。
(1)管道上存在泄漏孔时,在泄漏孔径固定的情况下泄漏孔处的流速及压力都与管内初始压力呈正相关。
(2)入口压力不变时,泄漏孔径的增大导致管道内部介质在上游的流动速度、泄漏孔处高压区和低压区的范围都增大;但在小孔范围内,泄漏孔径并不是影响管内的整体流量及泄漏速度的主要因素。
(3)泄漏的发生导致管道内部的压力呈现下降趋势,且初始压力越大这一下降趋势越明显,但最终都会逐渐变缓并趋于稳定值。
模拟结果显示,管道发生泄漏时,主流体受泄漏影响较小,管道内部压力和流速的波动不明显,主要在泄漏孔处差异较大;由于管壁约束作用,管壁附近流体的流速低于轴线处的流速,且越接近泄漏孔口,流体流速越大;但由于管内流体本身具有速度,泄漏孔处近壁面的流体由于内外压差向外泄漏时,泄漏孔壁面的阻碍致使部分流体瞬间停滞,使得泄漏孔处左右压力和流速呈不对称分布。试验结果表明,即使管道没有发生泄漏,其上下游间仍会存在压力差,与模拟测得无泄漏时管道上下游压力相等的结果不一致。因为实际管道运输中存在沿程损失,实际管道内的阻尼是无泄漏管中压力降的主要原因,压差即是介质流动过程损失能量的体现。
5 结论
本文采用Fluent软件模拟和试验分析相结合的方法,探究PE管道发生微小孔泄漏时流动参数的分布规律,结论如下:
(1)管道发生微小孔泄漏时,其内部主流体的压力、流速参数几乎不受影响,主要在泄漏孔处差异较大;管壁附近流体的流速较低,距离泄漏孔口越近,流体的流速越大。
(2)由于管内流体本身具有速度,部分流体在向外泄漏时,在泄漏孔壁面的影响下瞬间停滞,导致泄漏孔处左右压力和流速呈现不对称分布。且在这一刻流体的动能转化为压力能,使得根部边缘处产生两个负压区,泄漏孔根部产生一个高压区。泄漏口截面较小时,整个泄漏面大部分为负压。
(3)管道运输中,流动参数在一定程度上受泄漏孔径的影响,如当初始压力固定时,随着泄漏孔径增大,管道内部介质在上游的流动速度有上升趋势;同时,泄漏孔处低压区和高压区的范围增大,但小孔范围内泄漏孔径并非是影响泄漏参数的主要因素。
(4)管道上下游存在压差并不能作为判定泄漏孔是否存在的依据,实际应用中需要考虑输送过程中的沿程损失。

