残周期正弦波形总失真度的测量评价

梁志国，刘渊，何昭，张亦弛，吴娅辉

（1.航空工业北京长城计量测试技术研究所 计量与校准技术重点实验室，北京100095；2.中国计量科学研究院 信息与电子计量科学和测量技术研究所，北京100029）

0 引言

在复杂通讯信号的时频参数计量评价中，人们通常更加关注于能体现其各方面特性的“全波形”测量分析手段及结果。到目前为止，人们对于其信号带宽、频谱、功率等给予了极大关注［1-5］，因为它们事关信道宽度、容量等频谱资源的利用与分配。对于时域特征，由于其“复杂性”表述，并未形成统一的共识。

实际上，目前的复杂通讯信号，均不是任意波形信号，而是属于有确定载波的各种已调制信号，通常是正弦载波下的各种已调制信号。通过载波正弦信号的幅度、频率、相位等随时间的连续变化产生模拟调制效果；通过载波正弦信号的幅度、频率、相位等随时间的离散变化产生数字调制效果。

在参数连续变化为特征的模拟调制类已调信号中，复杂通讯信号可以看作是一个正弦载波的周波信号参数（幅度、频率、相位）随时间在连续变化而产生的结果。

在参数离散变化为特征的数字调制类已调信号中，复杂通讯信号可以看作是一段段正弦载波的周波信号阶跃跳变到下一个正弦载波的周波信号而产生的结果。即，由不同的稳定正弦周波信号和它们之间的阶跃跳变而产生的过渡过程相拼接而成的过程结果。

由此可见，复杂通讯信号的时域特征分析，可以归结为参量变化过程中的正弦周波特征分析和阶跃过渡过程的特征分析。在进行一段段正弦周波特征分析时，人们除了对其幅度、频率、相位、直流分量及其变化规律等予以特别关注外，其失真度或信噪比也是人们尤其关注的波形质量特征。它们通常包含了波形的畸变、噪声、内外电路和空间场产生的各种电磁干扰等，例如多径干扰、相邻信道窜扰。有单次干扰、周期性干扰、随机性干扰等不同种类。在复杂通讯信号全波形测量分析中，人们尤其关注每一个单独周波以及少于一个周波的残周期正弦周波的失真状态。另外，在一些和低频、超低频测量与控制有关的场合，由于时间因素、成本因素、失真反馈控制因素等要求，也需要在残周期条件下获得其失真度特性。

正弦波形失真有多种定义［6-10］，包括单一谐波分量的谐波失真、能谱比较均衡平稳的噪声失真、能谱明显高于噪声能谱但不属于谐波分量的杂波失真、以及包含全部谐波、杂波、噪声因素的总失真。它们通常都是在频域定义及实现的，需要使用谐波分析的手段和方法。因其无法进行有效的谐波分析，故在残周期条件下很难实现，只能借助于时域方法对其进行失真分析。

残周期正弦曲线拟合为解决该问题迎来契机［11］，使得残周期正弦曲线失真的评价成为可能。本文后续内容将主要讨论少于一个周波的残周期正弦波总失真度的测量评价，并试图找到一种技术解决之道。

1 基本原理方法

1.1 残周期正弦波总失真度

设带有谐波失真的正弦波形y（t）为

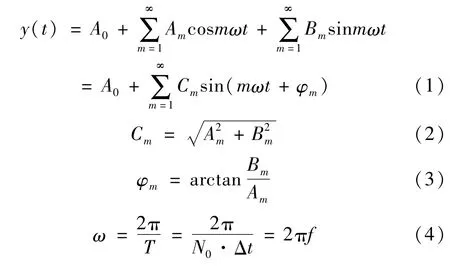
式中：Δt为信号采样间隔；N0为每个信号周期内含有的采样点数；T为基波周期；f为基波频率。

数据记录序列为已知时刻t0，t1，…，tn-1的y（t）的采集样本y0，y1，…，yn-1。四参数正弦曲线拟合过程，即为选取或寻找C1，f，φ1，A0，使式（5）所述残差平方和ε最小。

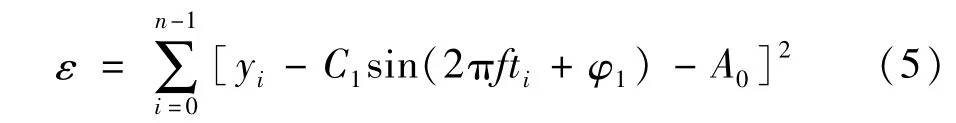
由式（5）的ε最小，可得拟合函数为

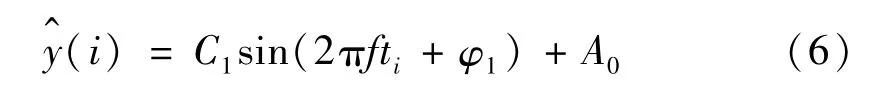
拟合残差有效值为

针对上述正弦波采样序列y0，y1，…，yn-1，使用残周期正弦曲线拟合法［11］，获得拟合参数C1，f，φ1，A0，并计算拟合残差有效值ρ。则有测量数据总失真度［6］

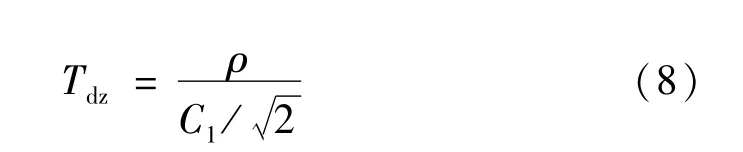
若无过高的准确度要求，可以使用Tdz表述被测残周期正弦信号的总失真度，若需要对测量系统带来的影响予以修正和补偿时，可以按照式（9）计算获得被测残周期输入信号的总失真度Tdi。

被测量输入信号总失真度［6］为

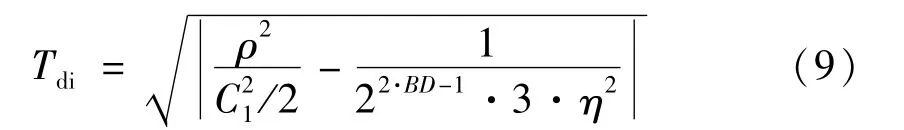
式中：BD为测量系统的动态有效位数；η为被测信号幅度范围与测量仪器量程范围的比值。

1.2 残周期正弦波的谐波失真

在上述残周期四参数正弦波拟合的基础上，按照式（4）可以计算出在已知采样间隔Δt下，每个基波中所包含的样本点数N0。而实际的采样序列｛yi，i＝0，…，n-1｝为少于一个波形周期的残周期序列，则有：

按式（10），（11）计算获得周期信号y（t）的谐波分量参数Am和Bm（m＝1，2，…）。

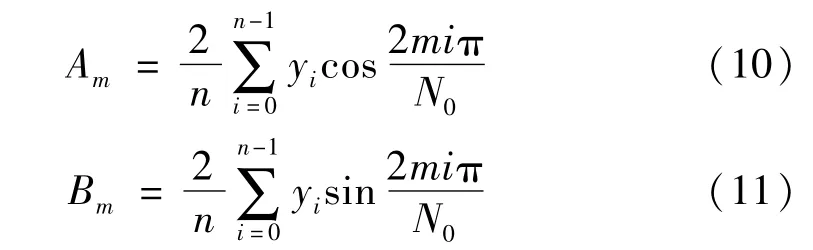
按式（2），（3）计算谐波幅度Cm和相位φm。

设定最高谐波阶次为M，则有信号y（t）的总谐波失真Tdh为［7-8］

2 实验验证

试验装置构成为［9］：

1）0.5 m大振幅、频率范围10 mHz～20 Hz的超低频振动标准装置；

2）A／D位数18 Bit、最高通道采集速率500 kSa／s、通道量程为±0.1～±10 V的NI PXI-6281型数据采集系统；

3）ASQ-1CA型位移传感器。

使用超低频振动标准装置，输出频率为50.000 mHz、位移幅度3.632 cm的正弦振动波形，激励位移传感器，设定数据采集系统的量程为±2.5 V，采样速率为200 Sa／s，数据样本点个数8000点。用数据采集系统执行采集，获得如图1所示的振动波形。

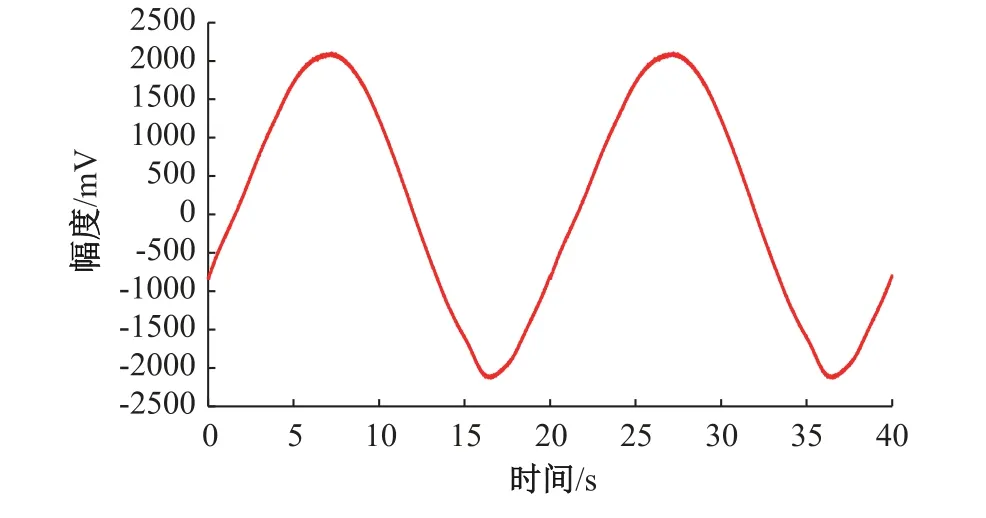
图1 位移传感器输出振动波形

执行四参数正弦波拟合［12］，拟合效果如图2所示。其中包含测量曲线、拟合曲线以及测量曲线与拟合曲线之间的差异值曲线。获得拟合参数为：拟合幅度2011.88 mV；频率50.047 mHz；初相位-32.93°；直流分量100.26 mV；残差有效值89.71 mV。

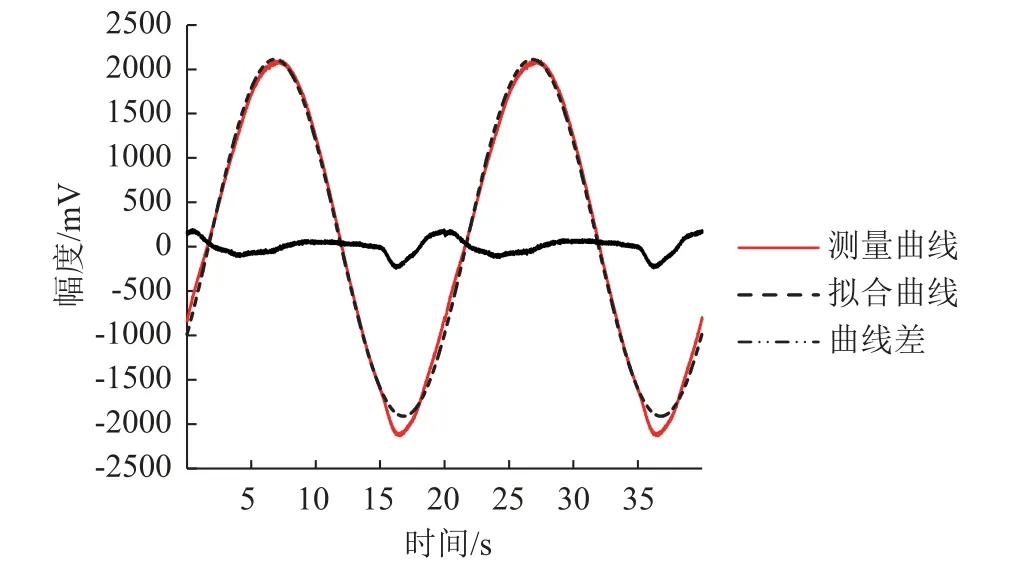
图2 位移传感器输出振动波形及拟合曲线、曲线差

按照式（8）的总失真度定义计算，获得该波形的总失真度为Tdz＝6.3%；按照式（9）计算Tdi≈Tdz。

从图1中截取不足一个波形周期的残周期正弦曲线如图3所示。

执行残周期四参数正弦波拟合［11］，拟合效果如图4所示。其中包含测量曲线、拟合曲线以及测量曲线与拟合曲线之间的差异值曲线。

图3 位移传感器输出振动波形残部（约0.6个波形周期）

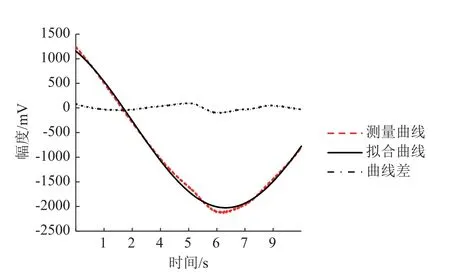
图4 位移传感器输出振动波形残周期拟合结果

获得拟合参数为：拟合幅度1746.778 mV；频率60.777 mHz；初相位124.67°；直流分量-279.4766 mV；残差有效值50.03 mV。

按照式（8）的总失真度定义计算，获得该波形的总失真度为Tdz＝3.5%；按照式（9）计算Tdi≈Tdz。

从多周期失真度和残周期失真度评价结果比较情况看，两者的量值存在差异，主要体现在局域拟合与总体拟合存在波形参数调控差异、波形失真分布不均造成的差异，它们都可能导致结果差异。两者的差异不够明显时，将表明正弦曲线失真分布比较均衡。本文所述方法具有稳定性与可行性，从图2和图4的曲线波形及差异的均衡性也说明了这一点。

3 问题讨论

综上所述，以残周期正弦拟合法为基础，用时域方式，可以获得残周期正弦波形的总失真度评价结果。

也可确定其某一谐波的失真情况。进行谐波失真分析时，难点在于基波频率参数的估计，即每周期采样点数N0的确定，该问题使用残周期正弦拟合可以获得解决。当噪声失真占比较大且分布比较均匀、随机性明显时，人们往往希望将噪声失真部分剔除，只评价谐波、杂波等畸变类失真，应用本文方法，可以获得谐波分析结果，但由于是残周期状态，其谐波分析结果误差较大，理由是谐波失真结果远大于总失真度评价结果，两者差异巨大，很难进行实际应用。其原因主要是，残周期拟合获得的基波频率相比多周期情况，误差较大；其次是，残周期因为信息不全，谐波之间正交性被破坏，导致各次谐波分量很难完全独立，你中有我，我中有你，重复部分导致合成结果变大。

此外，也可以使用局域失真的定义及评价方法处理残周期正弦波形失真［9］。即将波形按小邻域进行细分，再将小邻域内的波形失真细分为差模失真和共模失真，其差模失真的平均值，可视为噪声失真的平均值的一种估计。在能量守恒的前提下，从总失真中剔除差模失真部分，将获得只包含谐波、杂波类畸变失真的一种估计。相应的细节问题，有待后续研究予以解决。

4 结论

综上所述可见，本文所述内容主要是以残周期正弦拟合方法为基础，用时域方式定义并实现了残周期正弦波形总失真度的定量评估。并且经实验证实，在此残周期波形的基础上，使用谐波分析方法，很难获得其谐波失真的准确评价结果。

当残周期逐步扩展成完整周期后，残周期正弦失真的定义与评价方法与现有的正弦波形总失真度的定义完全相符合。属于提供了一种全新的波形参数定义、分析方法和技术手段，丰富和拓展了正弦波形失真的定义范畴。

本文所述方法，在以正弦波为载波的复杂通讯信号全波形深入分析和超低频振动等波形局部特征分析中，均有广泛的价值和良好的应用前景。