一种电动汽车变速时多速变速箱的拓扑变化模型

刘春玲， 张友坤

(1.长春工业大学人文信息学院， 长春 130000； 2.吉林大学汽车工程学院， 长春 130000)

随着化石燃料的迅速枯竭和新排放法规的制定，电动汽车逐渐成为汽车行业新的发展趋势。然而现有电动汽车由于能耗高，废气排放量大，普遍采用电气化和混合动力化[1-3]。多速变速器作为电动汽车的换挡机构，其性能决定了电动汽车的稳定性和舒适性，是一种拓扑可变的机构，啮合下的齿轮副在运行过程中会发生移位。当齿轮从一个速比转换到另一个速比时，发生传动拓扑变化，导致系统不连续，而其动态行为遵循当前的齿轮比[4]。

目前，中外学者对汽车变速箱的拓扑结构进行了大量研究，主要包括动力系统拓扑结构的设计、齿轮损失燃油经济性、变拓扑系统不同模型组合建模机制等方面[5-6]。然而传统的变速器传动系统建模时忽略了一个重要现象，即变速箱在换挡过程中的拓扑变化，导致对传动系统动态响应的不切实际的预测[7-8]。

对于电动汽车变速箱的研究，主要有两种拓扑变化模型，一是基于接触/冲击力学，其中弹簧阻尼系统用来表示接触/冲击面积[9-10]。利用该模型可以了解拓扑变化的影响，还可获得拓扑变化过程中接触/冲击力的变化过程，以便进行深入的动态分析。然而，由于该模型计算量大，无法实现在自然时间帧内拓扑变化所需的实时仿真。第二种模型基于脉冲-动量关系和恢复系数，得到拓扑变化时的不连续响应，该模型允许更大的时间步长，适合于实时仿真，然而，在处理系统状态的不连续跳变时仍然存在数值问题[11-12]。

针对上述分析，提出了一种新的变速箱拓扑变化模型，利用脉冲-动量关系和第一类拉格朗日方程，建立了模型的微分代数方程组，从而计算拓扑变化系统中速度不连续跳跃的模型，以解决电动汽车变速箱在换挡过程中的拓扑变化。分别利用传动试验台和MATLAB/Simulink进行了实验和仿真研究，通过仿真中的数学模型，对考虑速度跳跃的变速箱换挡进行了仿真研究。

1 拓扑变化模型

首先根据电动汽车变速过程的特点建立了新的考虑速度跳跃的变速箱拓扑变化模型，由于电动汽车多速变速系统是一个线性约束的传动系统，将变速箱动力学方程在一个拓扑变化周期内进行时间积分，以获得脉冲-动量关系，得到拓扑变化模型，进一步推导了由于拓扑变化导致的电动汽车多速变速器中速度跳跃的模型。对于具有n个广义坐标、以位置向量θ和s个约束方程中排列的完整系统，其位置约束方程为

φ(θ)=0s∈Rs,θ∈Rn,n>s

(1)

式中：θ表示位置向量，φ表示位置约束函数，n表示广义坐标个数。

通过对式(1)求导获得速度约束方程如下：

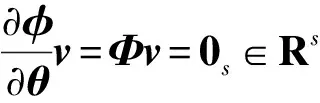
(2)

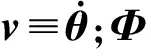
由于拉格朗日方程和约束在广义速度下都是线性的，因此不存在科氏力和离心力，得到系统约束数学模型表示为

Mv+ΦTλ=f(θ,v,t)

(3)

式(3)中：M表示n×n常质量矩阵，f(θ,v,t)表示作用力矩阵，λ表示s维拉格朗日乘子。

设T是Φ的正交补，因此，T∈Rn×n′，n′≡n-s，可得ΦT=0∈Rs×n′。将式(3)的两边相乘TT，消除拉格朗日乘数中的项，从而得到：

(4)

此外，令

v=Tw,w∈Rn′

(5)

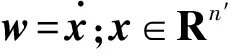
将式(5)代入式(4)，由于T是常数，式(4)可重新表示为

(6)

式(6)中：I≡TTMT∈Rn′×n′，τ=TTf。

假设在拓扑变化过程中广义坐标保持不变，而广义速度发生跳跃。t-和t+分别表示拓扑变化前后瞬间，且Δt=t+-t-的持续时间很小可忽略不计。由于广义坐标在所述区间内是常数，因此，矩阵T在[t-，t]中是常数，从而简化了式(6)的积分，并将方程两边乘以I-1可得：

Δw=I-1τ0

(7)

式(7)中：Δw表示速度跳跃；τ0表示作用力的脉冲，即式(6)中τ的时间积分。

为了获得式(7)中的速度跳跃Δw，需要首先确定脉冲τ0，τ0是τ的时间积分，其中τ=TTf，作用力f和T都依赖于传动设计。此外，变速器的作用力f取决于输入力矩、负载力矩和离合器力矩，通过建立传动数学模型，可以在仿真计算中得到力f，并通过实验验证结果的正确性。式(7)中的模型适用于所有类型的变速箱，模型本身不限于特定的传动布局，该模型依赖于齿轮换挡过程中的约束和作用力。因此，一旦获得约束和作用力，无论换挡类型如何，都可以计算出速度跳跃。

2 多速变速箱模型

在建立考虑速度跳跃的变速箱拓扑变化模型的基础上，进一步建立多速变速箱运动模型，以便于研究变速箱的运动变化。多速变速箱采用行星轮系统，由太阳轮、行星架、行星轮和环形轮四个部分组成，如图1所示。

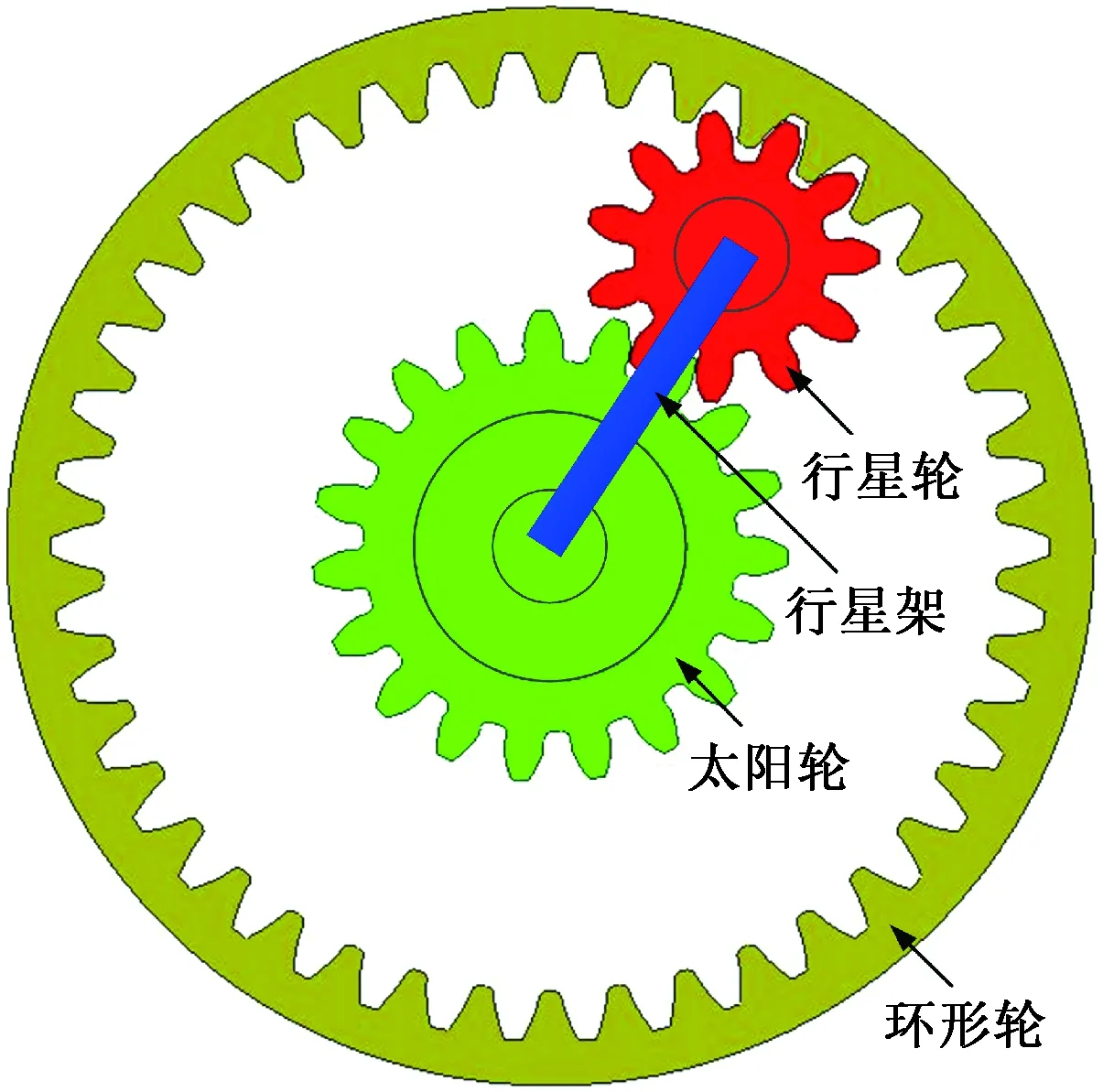
图1 行星轮系统结构图Fig.1 Structural diagram of planetary gear system

多速变速箱在模块化方面是唯一的，可根据车辆需要调节速比次数。故本文建立的多速变速箱由四个并联的行星轮系统组成，如图2所示。

图2 多速变速箱传动拓扑结构图Fig.2 Topological structure of multi-speed gearbox

图2中多速变速箱包括四个转动副，11个惯性元件，8个齿轮副(啮合)，4个环形轮离合器和2个多片离合器。

2.1 换挡机构模型

为了降低问题的复杂性，重点研究齿轮副变速传动系统中的拓扑变换模型，对图2种多变速箱传动拓扑结构进行简化，如图3所示。以太阳轮所在公共轴为系统输入，输出扭矩由公共连接架传递，该连接架直接连接到输出轴。

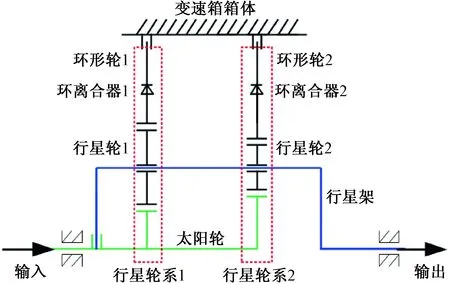
图3 变速箱二级变速传动拓扑结构图Fig.3 Topological structure of gearbox withtwo-stage transmission

从图3中可以看出，系统由两个行星齿轮系统组成，通过切换环离合器1和环离合器2实现换挡，换挡前后系统存在两种拓扑模型，当环离合器1闭合、环离合器2断开时，变速器传动比为5∶1，当环离合器1断开、环离合器2闭合时，变速器传动比为3.2∶1，在离合器切换过程中，系统从一个齿轮比转换到另一个齿轮比，拓扑结构发生改变。此外，传动速度在换挡过程中由于拓扑结构的变化而发生跳动。

2.2 二级变速箱数学模型

假设齿轮及其轮齿为刚性，则行星轮系统约束方程为

(8)

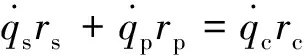
(9)

所述换挡机构由两个行星齿轮系统组成。由于太阳轴和行星架物理连接，存在两个额外的约束，可表示为

θs1=θs2≡θs

(10)

θc1=θc2≡θc

(11)

式中：下标1和2分别代表第一和第二行星齿轮系统。

在式(8)和式(9)的约束下，换挡机构齿轮系的总成为

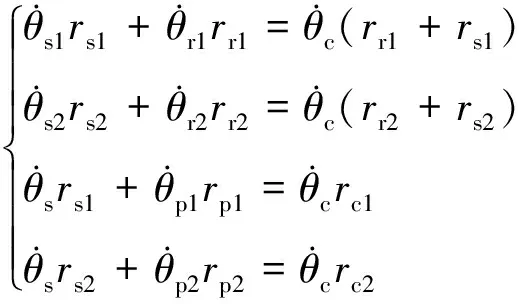
(12)

式(10)～式(12)中有六个约束条件，变速器有八个部件和相应的广义坐标，有两个自由度可以改变，这取决于啮合的齿轮比。用拉格朗日公式推导了传动的数学模型。广义坐标为θ=[θsθc]T，推导出数学模型为

(13)

式(13)中：A、B、C、a、b、c、d是为常数系数，其值如表1所示；cs为太阳轴轴承的阻尼系数，cc为行星架轴承阻尼系数；τd、τ1、τr1和τr2分别是电机、负载、第一环离合器和第二环离合器的力矩。

表1 常数系数表Table 1 Constant coefficient table

由于运动过程中环形轮加速度为零，根据扭矩平衡方程，可获得环齿轮1和环齿轮2的静态离合器力矩分别为

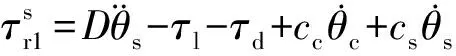
(14)

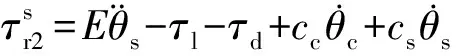
(15)

式中：D和E是表2中定义的常数系数。

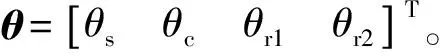
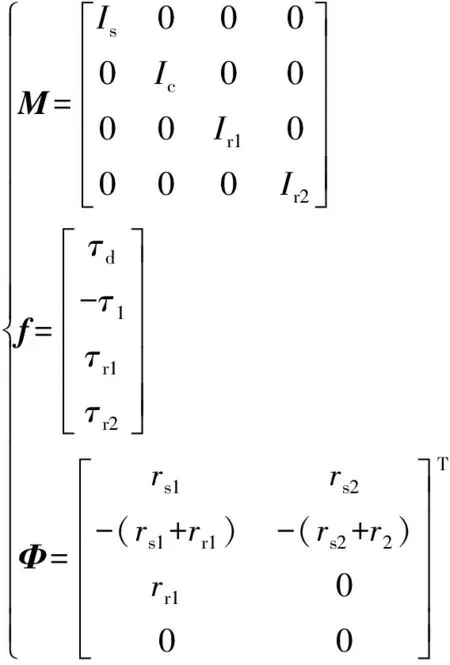
(16)

式中：Is、Ic、Ir1和Ir2分别表示太阳齿轮、环形轮、行星架和行星轮的转动惯量。

3 测试系统构建

3.1 仿真模型系统

根据构建的考虑速度跳跃拓扑变化模型和变速箱模型，建立如图4的变速箱仿真控制系统框图。

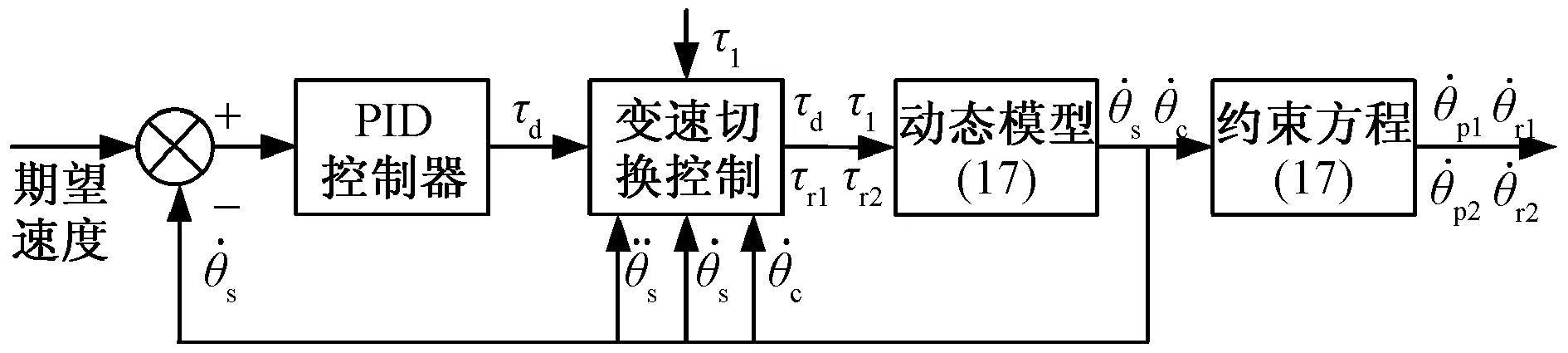
图4 变速箱仿真控制系统框图Fig.4 Block diagram of simulation control system for gearbox

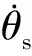
3.2 试验测量系统

为与仿真进行对比分析，在齿轮传动试验台上开展了试验测试，如图5所示，该试验台包括输入和输出两部分，采用对称结构，左侧为动力输入装置，第一个太阳齿轮传输输入扭矩，而第二组中的行星架传递输出扭矩，输入和负载由两个相同的无刷伺服电机GMBM80550-45提供。输入速度通过PID控制器保持与仿真相同，保持在369 r/min，而负载以3.24 N·m扭矩转矩提供反向运动。通过内置的电机编码器测量输入和输出角速度。

图5 齿轮传动试验台Fig.5 Gear drive test

根据实际系统模型，获得多速变速箱齿轮相关参数如表2所示。

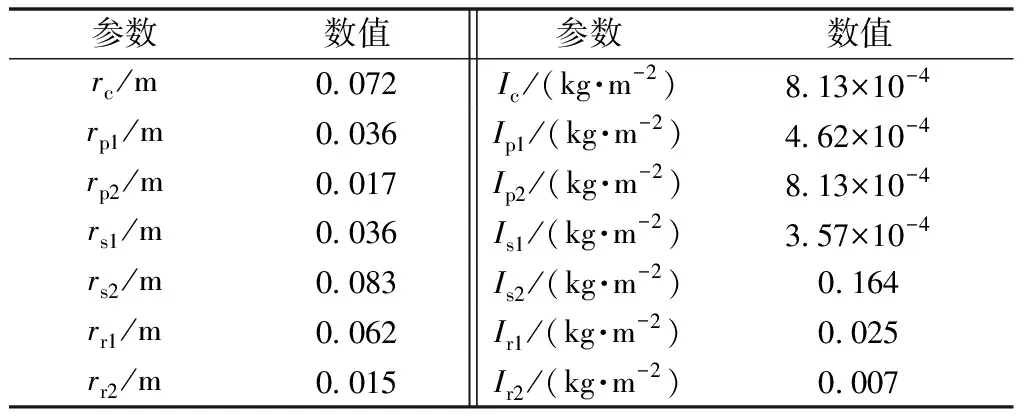
表2 多速变速箱齿轮相关参数Table 2 Gear parameters in multi-speed gearbox

基于表2中的参数值计算T和τ，如下所示：

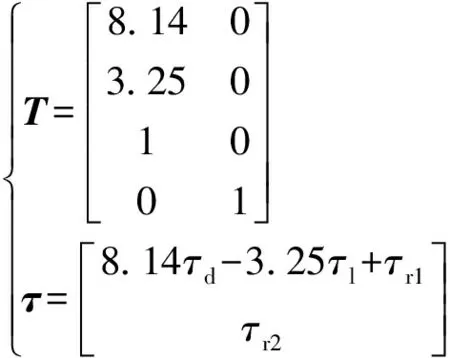
(17)

式(17)中：T是通过ΦT的QR分解得到的，它是T的一个正交补；T的下2×2块，只要得到的T是满秩的，就可以自由地选择一个零矩阵块。因此，最简单的选择是2×2恒等矩阵。

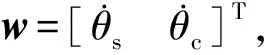
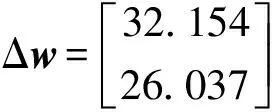
(18)

4 实验结果分析

为了验证本文建立拓扑变化模型的正确性，对不考虑速度突变的拓扑变化模型和本文提出的考虑速度跳跃拓扑变化模型进行了测试。

4.1 无拓扑变化模型结果

无拓扑变化模型下换挡过程中，对升挡和降挡过程输出速度进行仿真和试验研究，获得结果如图6所示。

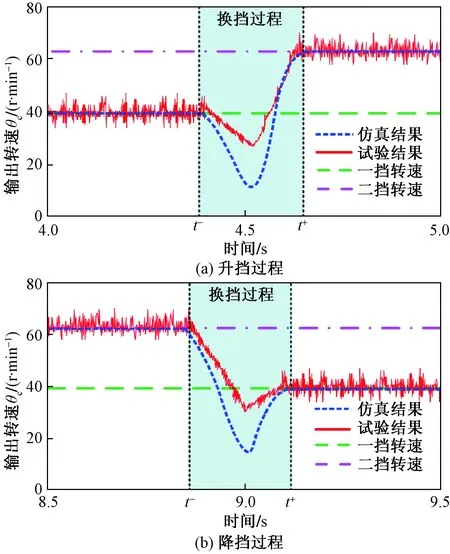
图6 不考虑速度突变时仿真试验结果Fig.6 Simulation and test results without consideringsudden change of velocity

从图6(a)中升挡过程可以看出，齿轮在t-=4.38 s时发生移动，进行换挡操作，在t+=4.65 s完成换挡操作，在移动前后输出速度发生跳跃，然而仿真结果中未记录跳跃过程。理论输入速度为40 r/min，换挡仿真速度下降到16.5 r/min，速度下降幅度达到41.25%，由于换挡周期与实验结果相匹配，仿真中输出速度发生大幅度下降，明显偏离实际换挡过程中速度的动态响应，因此无法根据仿真结果对换挡过程中的振动和控制研究提出切实有效的控制手段。从图6(b)中同样可以看出，齿轮在t-=8.87 s时发生移动，进行降挡操作，在t+=9.12 s完成换挡操作，整个过程中仿真结果同样出现较大的速度误差，而实际换挡过程中由于齿轮传动的约束作用，速度降低较小。

根据上述分析可知，在不考虑速度突变时，升挡和降挡过程中仿真结果均方法有效跟踪实际速度变化，换挡过程速度存在不连续性。

4.2 考虑拓扑变化模型结果

在不考虑速度跳跃下的仿真结果无法真实模拟电动汽车换挡过程的拓扑变化，为验证本文提出模型的正确性，将换挡过程分为换挡前、换挡和换挡后三个阶段，换挡阶段多速变速箱发生拓扑变化，并考虑在模型中，对不同输出速度下的升挡和降挡过程进行了研究。

对升挡和降挡过程输出速度进行仿真和试验研究，获得结果如图7所示。

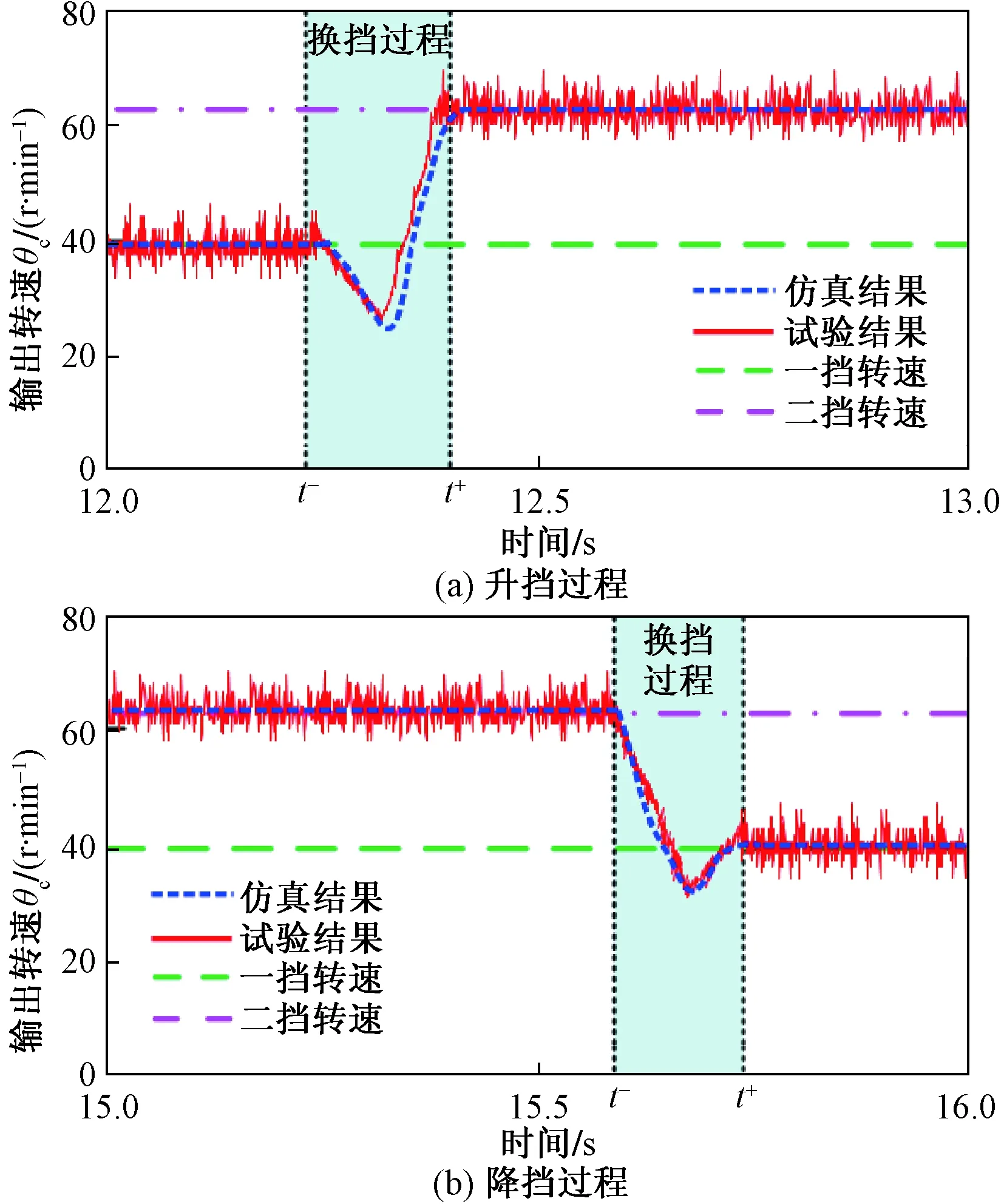
图7 考虑速度突变时仿真试验结果Fig.7 Simulation and test results consideringsudden change of velocity

从图7(a)中可以看出，由于拓扑变化，齿轮在t-=12.23 s处移动时发生速度跳跃，在t+=12.40 s时完成换挡操作，换挡总时间为0.17 s。在升挡换挡过程中，太阳轮齿轮的转速为32.154 r/min。PID控制器补偿了误差，使太阳齿轮在0.05 s内控制在所需的范围内，输出转速的速度跳跃为26.037 r/min，对比仿真和试验曲线可知，采用式(7)所述的具有速度跳跃的拓扑变化模型，升挡过程中仿真结果跟随试验结果，能有有效预测换挡过程中的动态变化。

从图7(b)中可以看出，在降挡过程中，速度变化趋势与升挡过程类似，仿真结果与试验结果曲线跟踪误差较小，表明提出的拓扑结构同样适用于降挡过程中速度变化的预测。

此外，车辆变速箱中行星轮和环形轮的动态响应无法测量，因此无法有效预测，对其进行准确的预测可以更好地控制和指导系统设计以提高传输性能。而根据本文建立的传动模型，可获得行星轮和环形轮的实时响应结果，从而能够预测变速器在不同工况下的动态响应。

5 结论

(1)提出了基于动力学原理的变速器拓扑变化模型，利用该模型计算了变速箱的速度跳跃，以解决电动汽车变速器在换挡过程中的多速非平滑变化问题。

(2)利用变速器试验台和MATLAB/Simulink 进行了试验和仿真验证，对常规模型和考虑包含速度跳跃的变速器拓扑变化模型进行了仿真对比。表明提出的拓扑变化模型可以有效预测变速过程中的变速箱的实际运动情况。

(3)在升挡和降挡过程中，考虑速度跳跃的拓扑变化模型仿真结果与试验结果跟踪误差明显减小，该拓扑变化模型适用于任何变速车辆变速箱。