异构型无人机群体并行任务分配算法
宋育武, 贾林通, 李 娟, 郭 浩
(1.空军哈尔滨飞行学院理论训练系,哈尔滨 150001; 2.哈尔滨工程大学水下机器人技术重点实验室,哈尔滨 150001;3.哈尔滨工程大学自动化学院,哈尔滨 150001)
无人机(unmanned aerial vehicle, UAV)根据任务使命的不同,装有等不同类型的任务载荷传感器,可遂行侦察、攻击等任务。随着UAV智能水平的提高及任务的复杂性,UAV群体协同作业成为未来空战领域的一种重要工作模式[1]。异构型UAV群体任务分配问题就是在考虑不同任务特性与UAV自身能力的前提下,为每个UAV分配需完成任务的集合,使得协同效能达到最优。在已有的研究中,现代智能优化算法因为具有易于实现、计算复杂度低、性能优越等特点,在无人系统的任务分配中得到广泛应用,比较常用的方法有粒子群算法[2-3]、蚁群算法[4]、遗传算法[5-6]、基于市场机制的拍卖算法[7]、合同网算法[8]等。文献[3]针对标准量子粒子群算法对多无人机任务分配中离散狭长解空间适应性差的问题,提出了基于粒子收敛程度的自适应惯性权重与量子门变异算子,将标准量子粒子群算法进行改进。文献[7]研究异构无人机对不同类型目标执行侦察、打击和评估任务的协同任务分配问题,采用信息论中熵的变化量对侦察与评估任务中所获取的信息量进行度量, 设计了基于相邻局部通信的分布式拍卖算法, 实现了多无人机协同任务分配问题的优化求解。文献[8]针对传统合同网的任务分配算法在动态环境下存在效率较低的问题,通过引入任务信任度和负载均衡度指标,对传统合同网的任务分配方法进行改进。本文针对装有异构型UAV群体,建立多UAV任务分配模模型,以时间消耗最短为优化目标,对UAV执行区域进行子域划分,最大限度地利用可用的UAV,建立多UAV任务分配模型及最优化函数,对基本遗传算法进行改进,以期有效解决了并行任务下的任务分配。
1 问题描述
异构型UAV群体由具备不同功能的个体UAV组成。在对UAV进行任务分配时必须考虑各方面因素。首先,异构型UAV群体在协作完成复杂使命时,个体UAV由于功能的差异及各种任务的不同,决定了不同任务可供选择的接受者不同。其次,多功能UAV(如果有能力)在某一区域能够同时执行多个并行子任务,因而可以有效减少完成任务的时间。
为了使异构UAV群体能够在完成总体任务的基础上,实现对数量及时间的优化,必须建立完善的群体UAV任务分配模型,以保证任务的合理分配,并且起到优化目标的作用。
讨论的异构型多UAV系统任务分配问题可描述为:使用分散在Nstart不同出发区域且装有不同类型任务传感器的UAV对Nareas个区域进行数据采集、目标搜索等任务,协同任务分配的目标满足所有约束条件下,以最少数量的UAV或以最短时间实现对异构型群体UAV的任务分配完成该任务。
2 并行任务分配模型
2.1 并行任务概念
能够执行并行任务是UAV智能化的体现之一,也是模型能够优化目标函数的关键。UAV执行并行任务,顾名思义,是指一个UAV可以同时执行多个子任务或者一个任务可由多个UAV同时执行。
异构型UAV系统由功能不同的UAV组成,各UAV之间的传感器配置可能不尽相同,UAV个体也可能配备多种不同类型的传感器。并行任务[9]主要是从以下两个方面来考虑。
单个UAV执行并行任务。主要是指在一个区域分布着需要多种传感器的多个子任务,而某个UAV单体均配备这些类型的传感器,倘若该区域的所有子任务均分配给该UAV,则该UAV能够同时执行这些子任务,并且各任务在执行时,相互之间互不干扰。
多UAV同时执行并行任务。是指一个区域分布着需要某种传感器的子任务,而配备有该类型的传感器的多个UAV能够同时执行该任务,完成该任务的时间会相应减少。
如某一区域的任务有两个子任务:子任务1为需要传感器S1完成的任务,完成时间为30 min;子任务2为需要传感器S2完成的任务,完成时间为40 min。有两个UAV均配备这传感器。
在不受时间、能源限制的条件下,这两个UAV均可以独立完成该任务,如果由单个UAV执行该完成任务,则可以同时执行这两个子任务,并且各子任务之间互不干扰,那么执行子任务1时需要30 min,执行子任务2需要40 min,最后完成总任务的总时间只需40 min。在使用这两个UAV共同完成该任务时,需要将该重新划分为两个相同的区域,两个UAV分别执行其中一个区域,且同时执行各自任务区域的任务,则总任务只需要20 min便可完成。UAV系统在执行这种并行任务时,可以减少完成每个UAV的扫描时间,从而可以起到减少总任务时间的作用,但也可能使UAV的使用数量增多。
2.2 假设条件
群体UAV任务分配与任务协调问题中的相关元素可以用四元组〈V,A,S,C〉来表示,V={1,2,…,Nuav}是UAV集合,每个UAV装配有不同的传感器;A={a1,a2,…,ak,…,ap}是任务执行区域集合,其中1≤k≤p,每个侦察区域ak的大小不一定相同,完成该区域的任务可能需要多种类型的传感器,S={1,2,…,Nsensor}是传感器集合;C是约束条件的集合,根据用户任务的需求约束条件不相同。
为了便于讨论问题,又不失一般性,在建立任务分配模型之前,作如下假设。
(1)在任务分配前,任务区已划分完毕,而且彼此之间相邻,从而形成了不同的子任务,接受到子任务的UAV可以准确到达该区域执行任务。
(2)不考虑UAV从出发点到任务作业区的时间和能源消耗,而仅仅考虑在任务作业区域内的时间。
(3)具备某一相同功能的不同UAV去完成某一子任务时,所需要的时间相同。
(4)具备某一相同功能的不同UAV可以在同一区域同时执行任务,彼此之间互不干扰,效果同一个UAV执行任务一样,但完成任务时间不同。
(5)任务作业区域如果存在重叠,可以进行重新划分。
(6)UAV不受工作时间,能源限制,且具有相同的物理尺寸和效率。
2.3 时间消耗最短的任务分配模型
以时间消耗最短为目标实现对异构型群体UAV的任务分配,任务区域划分为不同的子区域,且多个UAV可以同时执行子任务,这将会使不同的任务分配方案下总任务完成时间不同。该模型用以在以上所做各种假设下,实现对总体任务时间的优化,可以建立一个整数线性规划(ILP)模型,参数定义如表1所示。

表1 ILP模型中所使用的参数定义Table 1 Parameter definition of used in ILP model
异构型UAV群体面向多个目标区域进行任务分配问题时,为了能够使UAV群体能够在最短时间内完成总体任务,进行任务分配的问题可以表述为[10]

(1)
式(1)中:∀i∈V,∀j∈S,∀k∈A
第一个约束条件表明:任务工作区域k需要第j种传感器,即xsa(j,k)=1,则到该区域执行任务的UAV可以不止一个,否则不使用UAV,这种分配方案将能够使多UAV执行并行任务,起到减少总任务时间的作用.
第二个约束条件表明:如果任务工作区域k需要第j种传感器,且第i个UAV到该区域执行任务,那么该UAV必须配备该类型传感器,否则该UAV可以不具备此种传感器,此约束条件是对UAV传感器的配备所做出的要求。
第三个约束条件表明:如果第i个UAV被派遣到需要某种传感器的某个特定区域,表明该UAV已被使用;该约束条件是为了判断UAV是否被使用。
3 异构多UAV并行任务优化分配的遗传算法
遗传算法以编码空间代替参数空间,以适应度函数为评价依据,以编码群体为进化基础,以对群体中个体位串的遗传操作实现选择和遗传机制,建立起一个迭代过程。在这一过程中,通过随机重组编码位串中重要的基因,使新一代的位串集合优于老一代的位串集合,群体的个体不断进化,逐渐接近最优解,最终达到求解问题的目的。
3.1 UAV群体并行任务分配的编码
种群中个体的编码结构(染色体的编码方式)属于知识表示范畴。遗传算法中常用的编码方式有二进制编码、实数或浮点数编码、二维染色体编码树结构编码等。
3.1.1 任务序列的编码方案
UAV的多任务分配问题首先需要了解系统的任务组成,然后对总任务进行划分,将划分的子任务进行统一编号,如表2所示,表中列出了各区域所需要的传感器,1代表对应区域需要相应类型的传感器完成该任务,0表示没有任务。任务编号如下:任务1为(S1,a1)、任务2为(S1,a2)、任务3为(S1,a3)。

表2 任务描述Table 2 Description of mission
为了计算出UAV在每个任务区域的任务时间,除了以上对所有任务进行编号外,该算法还必须对任务区的子任务进行编号。如表2所示,任务区域编号如下:mission(a1,1)为任务1,表示任务区域a1的第一个任务为任务1;mission(a1,2)为任务4,表示任务区域a1的第二个任务为任务4。
3.1.2 传感器配备的描述
每个UAV配备的传感器的种类如表3所示,以二进制表示各UAV的配备情况,1表示相应的UAV配备有该种类型的传感器,否则未配备相应传感器。
3.1.3 模型可行解的产生
在对模型的任务序列进行编号和每个UAV传感器配备后,就可以确定各子任务的执行者的集合,从而产生分配模型的可行解。

表3 装备配备描述Table 3 Description of sensor equipment
任务分配时执行各区域子任务的UAV个数可以不止一个,即单一子任务不仅须考虑执行者的不同,还需要考虑执行者个数的不同,采用如下两层编码方式。
任务序列:1,2,3,4,5,6,7,8,…。
UAV编号:1,2,0,4;0,2,3,0;1,2,3,4;0,0,0,0;1,0,3,4;…。
以上为随机产生的任务分配方案,任务1可以由V1、V2、V3、V4四个UAV去完成该任务,但V3并没有分配该任务;任务2有V2,V3两个UAV去执行,V1、V4并没有分配该任务…,可以看到分配方案中任务4并没有分配UAV完成该任务,这显然不满足任务分配约束条件。
3.2 适应度函数的建立
上述编码方式只满足了模型的部分约束条件,为了将原约束问题转化为无约束问题,可以对模型适应度函数施加一个惩罚项,便可将带约束条件的问题转变为无约束问题。
惩罚函数如下:

(2)
式(2)中:1≤m≤maxmission。
综合目标函数和惩罚函数得出适应度函数如下:
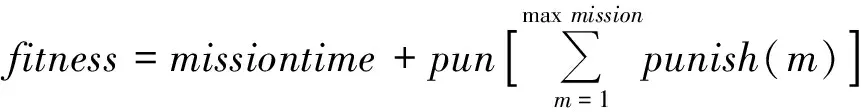
(3)
式(3)中:maxmission表示任务的总数;pun表示惩罚系数。
计算适应度时,可以将惩罚系数pun设置较大,由于每个染色体对应全部任务的一个分配方案,将得出每个染色体的适应度,但是如果该染色体只满足部分约束条件而不能满足全部的约束条件,罚函数将不为0,较大的惩罚系数pun将会使染色体的适应度变得很大,染色体的适应能力将大大降低,在分配方案择优时便可根据适应度剔除不满足约束条件染色体,从而将原约束问题转变为无约束问题。
3.3 算子选取
3.3.1 交叉策略
设置好染色体总数以后,将前一半染色体随机与后一半染色体进行交叉,交叉时随机产生一个位置,互换该位置到最后的基因组成,并更新原染色体,图1给出了遗传算法在该问题中的交叉方式。
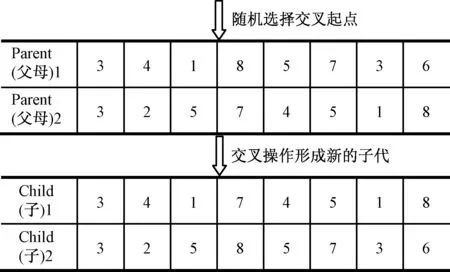
图1 交叉策略Fig.1 Crossing strategy
3.3.2 变异策略
为了使结果不至陷入局部最优,必须进行染色体的变异。采用基本变异策略变异时只改变随机产生的位置处的任务分配方案,发现结果并不能实现最优。为了得到最优解,跳出局部最优,对变异策略进行改进。
为了减少每个UAV在每个区域的完成相应任务的时间,可以使任务区域尽可能地使用较多的UAV,从而可以起到减小UAV的时间。在变异策略设计时,随机选择一条染色体及一个位串,将该位串变异成所有它能变异成的基因,其变异策略示意图如图2所示。采用该变异策略的目的是由于任务分配目标是最短时间完成任务,对每一个任务最大限度的派遣UAV才能减小该任务的时间,从而起到减小总任务的时间的作用。
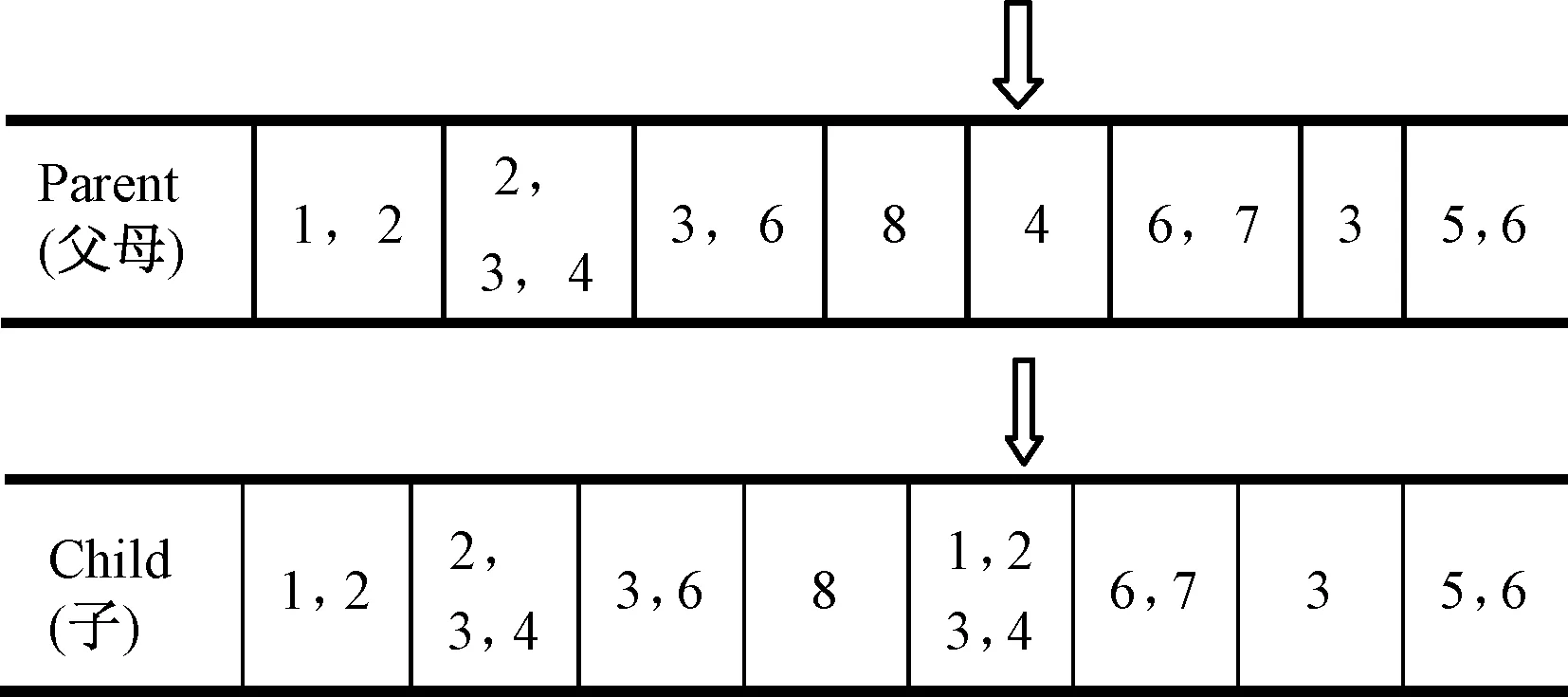
图2 变异策略Fig.2 Mutation strategy
并行任务分配算法步骤如下。
Step1参数初始化。随机产生初始种群gen(0);确定最大遗传代数T;置遗传代数计数器t为0。
Step2对种群中所有个体的适应度进行评价。
Step3选择操作。对群体按照轮盘赌进行选择。
Step4交叉操作。对群体按照交叉算子进行交叉操作。
Step5变异操作。对群体按照变异算子进行变异操作。群体gen(t)按照选择、交叉和变异操作后就得到了下一代的群体gen(t+1)。
Step6适应度计算。
Step7算法终止判断。如果t≤T,则gent← gen(t+1),转到Step 2:如果t>T,就输出在遗传进化过程中适应度最大的解,算法结束。
4 仿真算例
4.1 仿真案例的基本描述
仿真案例[10]如图3所示,为了验证改进的遗传算法在求解异构型群体UAV任务分配模型的有效性,各任务区之间相互重叠,图3中分布着6个任务区域,由于任务区域的重叠,而且各区域所需要的传感器种类不同,会导致同一区域中重叠区域与未重叠区域所需要的UAV种类不同,因而必须对任务区域进行更具体的划分,如图4所示,图4中列出了各区域划分的结果,将原任务区域划分成了11个新的区域。表4列出了各任务区域所需要的传感器类型及完成该任务的时间。

图3 仿真案例任务区域分布 Fig.3 Mission areas distribution

图4 多区域的划分示意Fig.4 New mission muti-areas distribution
表5列出了用于完成该任务的异构型UAV系统的组成及传感器配备情况,共有8个UAV参加任务,V1,V2均配备传感器S1,S2;V3,V4配备传感器S2,S3;V5,V6只配备传感器S4;V7,V8均配备传感器S5,S6。此例中将任务限定在400 min以内。
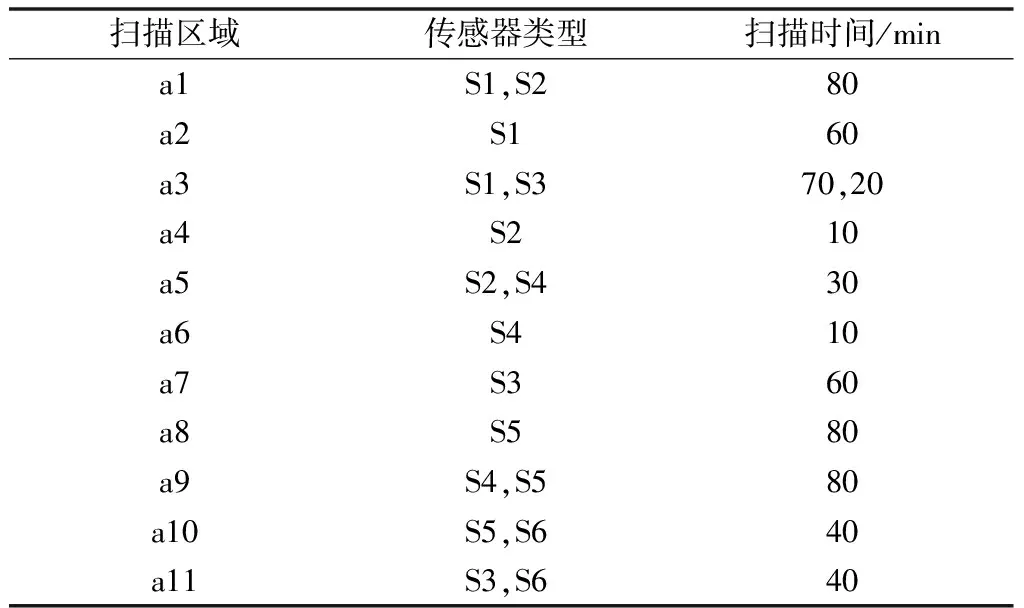
表4 仿真案例的任务描述Table 4 Mission description of simulation

表5 异构型UAV系统的组成Table 5 Heterogeneous UAV sensor equipment
4.2 仿真结果
通过改进的遗传算法来求解该案例时,其仿真结果如表6所示;从仿真结果可知完成总任务的时间为120 min,使用了8个UAV。
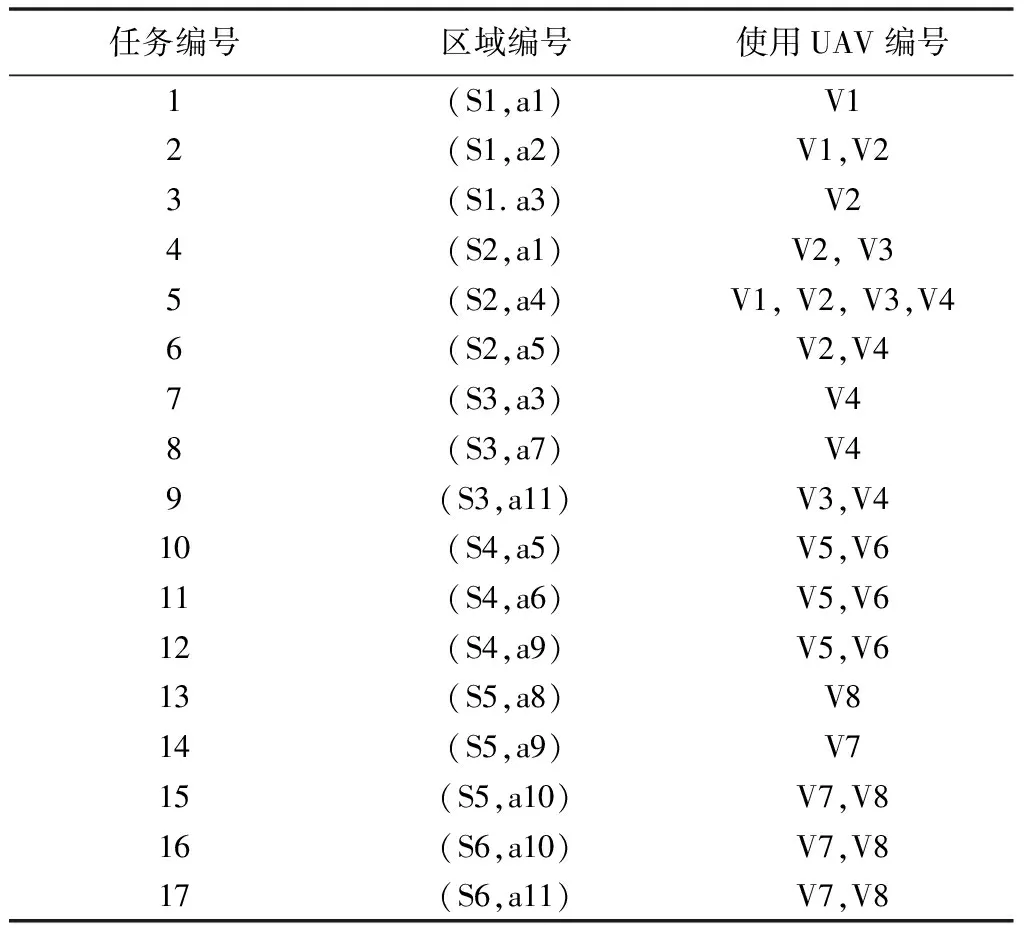
表6 任务分配方案Table 6 Task allocation scheme
与此同时采用了基本遗传算法来求解此案例,并与改进的遗传算法进行了对比,结果如图5所示。
通过以上对比结果可知,运用基本遗传算法求解该案例时,进化到5代时就出现了最优值,完成任务的时间为140 min,但采用改进的遗传算法的求解时,进化到7代时出现了最优值,但完成任务的时间也为120 min。通过对比可知改进的遗传算法加大了进化到该最优值的代数,却实现了对时间的优化。究其原因,UAV能够执行并行任务,UAV的使用时间为在各区域中使用时间之和,为此需要增多各区域中各任务的执行者个数以减少各UAV在每个区域的使用时间。因而改进的遗传算法能够起到的减小进化到最优值的代数的作用,在更为复杂的任务构成案例中将会起到优化目标函数的效果。

图5 仿真结果对比Fig.5 Contrast of simulation results
5 结论
研究了异构型UAV群体并行任务分配的问题,以时间消耗最短为优化目标,建立个整数线性规划的任务优化分配模型。通过建立最优化函数,运用改进的遗传算法完成了异构型群体UAV并行任务分配问题的求解,重点对编码方案、适应度函数和变异策略进行了详细设计。仿真结果表明该算法能够对异构型群体UAV并行任务问题的成功求解,具有较强的寻优能力,极大地缩短了寻优的时间,从而提高了整体任务的执行效率。通信拓扑的优化,以及变动目标环境下的协同式的任务分配是今后研究的重点。

