基于优化遗传算法城市立体车库信号调度算法的研究*
张书茂
(安徽城市管理职业学院,安徽合肥 230000)
0.引言
近年来,经济的高速发展,生活质量的不断提高,除了公用车辆的数量相对稳定,私家车数量上迅速增长,立体车库应运而生,目前大都是地下城市立体车库,同普通停车场主要区别是层数的增加,有一部分立体车库,已经安装有升降装置的,在空间上得到了一定的优化利用,但是相当一部分还是依据信号的顺序对升降装置即堆垛机的调度控制,即单体控制[1],那么对堆垛机的调度优化方面还需要进一步的研究,提出了一种基于遗传算法堆垛机的路径优化算法[2],为立体车库的堆垛机路径优化提供参考。
1.遗传算法
1.1 相关概念
1975 年J.Holland 教授提出遗传算法简称GA。其主要思想是通过多次迭代方式在实际问题空间里,求解达到一定程度的最优解。
1.2 常用操作
在遗传算法迭代的过程中,因为只考虑内部信息,适应度函数对迭代的次数和运行时间起着决定性作用。适应度函数g(x)主要有:(1)目标函数为参数;(2)估算参数Dmax|min为参数;(3)通过界限值D 参数(保守估计)。
实际运行中,会产生两种极端的现象:
第一种:差异比较大特殊的个体,对优化选择的趋势影响到全局。第二种:差异比较小的个体,对优化效率有一定的影响。为了减少以上个体的数量,对适应度函数g(x)要满足如下要求:
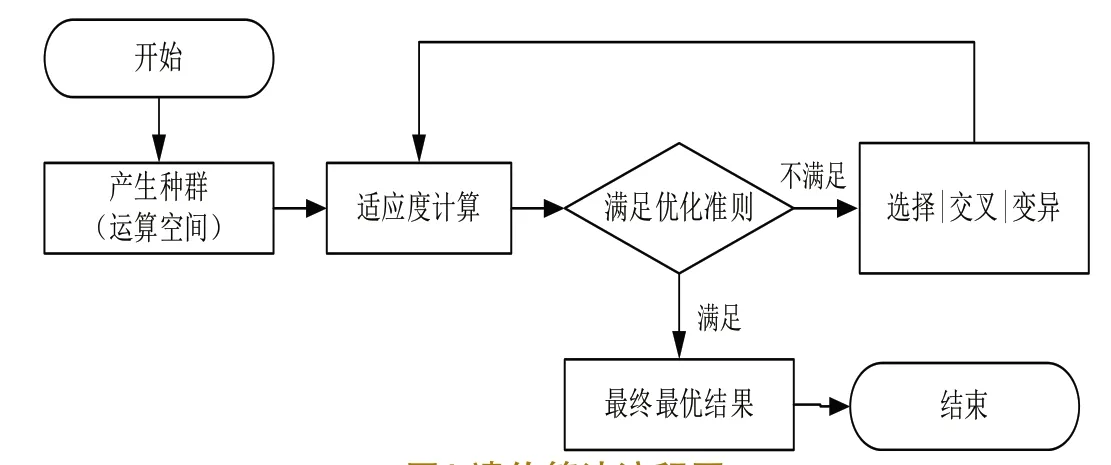
图1 遗传算法流程图
(1)g(x)函数要连续性,正值区间,具体值。
(2)g(x)在保证目标函数的条件下,简单线性化。
(3)g(x)的参数在达到目标函数要求范围内,通用化。
1.3 算法流程(图1)
2.遗传算法的改进
2.1 相关思路
在遗传算法求解最短路径的问题上,除了适应度g(x)函数有很重要的特点外,在初始化种群中求解的空间范围中的个体也很重要,通常是随机选取后进行迭代运算[3],那么在求解空间的选择或者样本空间的选择也很重要,不同的样本空间的选择,得到的结果也是不同的,为了保证在样本空间具有一定的连续性相关性,提高遗传算法的运行时间和空间的效率,引入蚁群算法(Ant Colony algorithm),对求解空间的样本进行优化,提升遗传算法。
蚁群算法是通过蚁群寻找食物的整个过程的思想,即个体之间交流信息找到最佳路径。
2.2 相关概念
假设立体车库有n 个停车位,先求解样本空间然后求解最佳路径。其中n 个停车位表示为n 个节点,dij代表第i 和第j 个节点的距离,其中i,j ∈n。
n个停车位对应n个蚂蚁,作为各个蚂蚁的位置的初始化。

相关说明: Aijα(t)表示节点i 与节点j,t 时刻路径上的剩余信息。 Bijβ(t)表示节点i 与节点j 的概率值,通常用1/dij表示,其中的α 和β 是用来调节的参数,该公式表明:选中的概率与该节点的信息量成正比,与距离成反比。
每个蚂蚁k 都有一个线性表结构L 与之对应,用来记录所访问过的节点。其中用ρ 表示L 的内容更替的程度[4]。
所有节点完成一次遍历后,每个节点的信息调整如下:

2.3 改进方法
步骤1:n 个蚂蚁对应n 个停车位。

(3)循环结束条件进行判断,满足跳出循环,反之继续循环。
步骤4:通过步骤3 的结果然后进行遗传算法的求解。
2.4 相关说明
通过分析,α=1,β=5,ρ=0.5 比较稳定,C,Q 基本没有影响,一般取值为C=10,Q=100。特别说明一点:一般循环体选用次数或者两次遗传运算结果的差异值[6](差异值允许的一定范围)。
3.数据分析

表1 空停车位表
假设在某一个立体车库的某层车库,每个停车位之间长度为1m,宽度也为1m,堆垛机的运行速度匀速为1m/s,本仿真实验不考虑时间进行测试,本车库总共停车位为225 个,其中209 已经停满,还有16 个车位为空位,空车位的坐标,如表1 所示。
(2)通过传统的遗传算法得的路径为:A-C-J-F-B-IE-M-H-P-D-G-L-K-O-N-A,对应的路径长度为:9+8+7+5+10+2+4+6+13+5+8+10+5+10+3+11=116,因为传统的遗传算法求得结果不一定是最优的结果,是相对优解(允许在一定的范围)。
(3)通过蚁群算法优化初始种群,再进行遗传算法求解最短路径:A-F-B-E-I-M-H-G-P-J-L-N-O-B-K-D-A,对应的路径长度:8+5+10+2+4+6+10+5+5+2+4+3+3+9+3+21=100。
可以得到传统遗传算法得到解是相对优解,通过蚁群算法初始化种群后在进行遗传运算得到的解更好一些。
通过算法得分析可以得到,通过蚁群算法初始化种群后,遗传算法得运算空间的基本解决,在通过适应度函数进行微调就基本达到相对的优解。
4.结语
本文探讨了立体车库信号调度堆垛机的最短路径的问题,讨论的案例是在平面二维车库进行的,适应度的平方差比较小,边缘的适应度高的节点以及客户停车时间的参数对路径的选择的影响有待进一步的研究。

