执行器失效的建筑结构有限时间稳定补偿控制

巩琪娟, 黄堃锋, 马灿洪, 严彦成, 朱厚耀, 王建晖

(广州大学 机械与电气工程学院, 广东 广州 510006)

为减小地震波对建筑结构的影响，已证实主动振动控制(AVC)策略可以通过控制方法与主动质量阻尼器相结合的方法，在建筑结构中引入一种外源能量来抑制振动.为保证建筑结构的稳定，文献[1]中提出了传统的比例导数(PD)和比例积分导数(PID)等控制方法.对于一些最优主动控制问题，已有线性二次(LQ)控制、线性二次调节器(LQR)控制和线性二次高斯(LQG)等控制方法.为处理地震波的问题，针对结构系统的抗震系统提出的滑模控制方法[2]以及H无穷的主动控制策略(H∞ AVC)[3]中假定地震波是已知的或在一定范围内有限的.

执行器失效会减弱对振动的抑制作用.为减少损失，在非线性控制理论中已经发展了许多失效补偿方法，如文献[4]中采用自适应控制技术对非线性系统进行执行机构失效补偿.

由于大多数方法都将系统的李雅普洛夫稳定性归结为渐近稳定研究领域，即稳定时间将趋于无穷.故在探索有限时间控制方法方面，文献[5]中设计了切换控制系统的有限时间稳定性；针对高阶非线性系统，文献[6]中提出了一种反馈有限时间控制方法；结合反推技术和滑模控制，文献[7]中设计了一种用于航天器姿态跟踪的有限时间滑模控制；有限时间稳定控制被广泛应用于有限时间稳定特性方面.

本文研究建筑结构振动的有限时间稳定补偿问题，提出了一种模糊自适应有限时间模糊补偿控制方法.将地震波视为系统中的非线性项，用模糊逻辑系统近似设计了有限时间自适应故障补偿振动控制的方法.利用有限时间稳定性准则，证明了该方法能够保证不确定的执行器失效系统在有限时间内保持稳定.不同失效情况下的仿真表明本文提出的方法对于使建筑结构在有限时间内保持稳定更加有效.

1 系统的模型和问题描述

1.1 建筑结构系统的数学模型

1.1.1n层建筑结构的动力方程为[1]

(1)

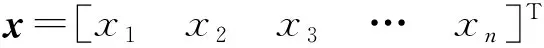
1.1.2 定义子系统数学模型为

(2)

可将系统(1)转化为以下子系统：

i=1,2,3,…,n

(3)

1.2 不确定的执行器失效模型

本文考虑了两种不同程度的执行器失效情况：①部分失效(PLOE)：因为部分损坏或缺乏动力等因素而导致执行器的输出只产生部分理想；②完全失效(TLOE)：因为完全损坏或失灵而导致的执行器输出全部失效.

设vij(t)=vi(t),∀j∈A.vi(t)，建筑结构系统的不确定执行机构失效可以被描述为

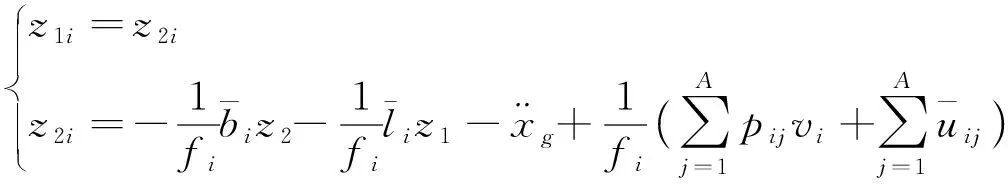
i=1,2,3,…,n

(4)

假设1：完全失效的执行器数量不超过A-1，并且剩余的执行器能够满足控制要求.

1.3 模糊逻辑系统的逼近研究

1.3.1 模糊逻辑系统数学模型

为了提高抗震效果，将地震波的加速度视为一个未知的时变非线性函数，对近似未知非线性项采用模糊逻辑系统(FLSs)逼近研究，模糊逻辑系统描述为

(5)

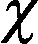
(6)

1.3.2 地震波加速度的模糊逻辑系统逼近

(7)

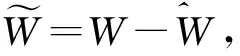
在执行器失效的n层建筑结构系统中有n个子系统需要稳定，对于第i个子系统(第i层)，控制器驱动执行器可能发生故障，为了动态补偿,地震波加速度用模糊逻辑系统逼近，控制器参数可以在线调整，以补偿执行器失效.

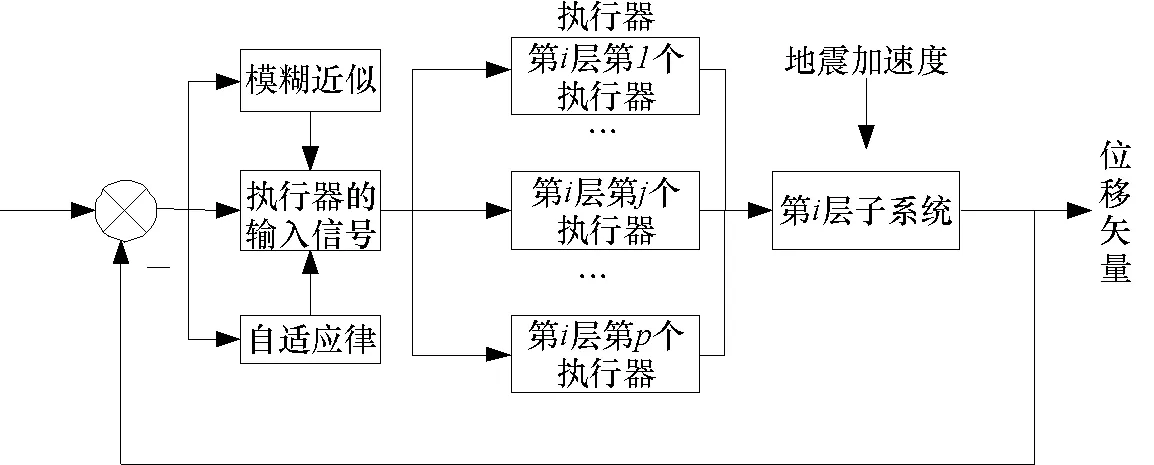
图1 n层建筑结构失效控制结构图Fig.1 Failure control structure drawing of n-storey building structureFig.1 Failure control structure drawing of n-storey building structure

下列引理用于控制设计：

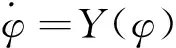
(8)

其中,W(φ)是正定函数，并a>0,δ>0,1>β>0.

引理2[9]对于xi∈R,i=1,2,3,…,n,0<ρ≤1有

(9)

引理3[10]对于φ∈R和φ，有

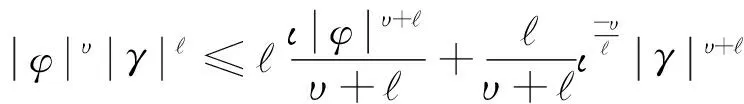
(10)

其中,υ和是任意的积极变量.

2 控制方法设计及稳定性分析

2.1 控制方法设计

控制对象为系统(4)的有限时间稳定控制器，保证建筑结构在有限时间内位移趋于小集合.根据控制对象，建立以下误差方程：

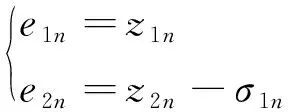
(11)

其中,σ1i,i=1,2,3...n是虚拟控制器.σi被设计为

(12)

定义以下内容：

(13)

为了补偿执行机构故障的有效性，控制设计中采用自适应控制理论，控制输入可表示为：

(14)

其中，w=[σ2i1]T；

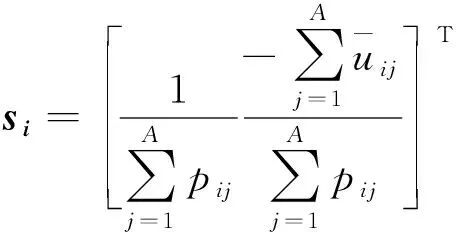
设计自适应律为

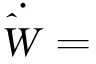
(15)

(16)

2.2 稳定性分析

理论1:在假设1的基础上，考虑具有不确定致动器故障的建筑结构系统如式(4)，具有自适应律(15)和(16)的控制器(14)可以保证所有的关闭系统信号都是有界的.z1的状态在有限时间内趋于小集合.

综上，分析得：

(17)

(18)

选择正李雅普诺夫函数为

(19)

(20)

选择一个新的李雅普洛夫函数：

(21)

根据引理3分析，通过推导得：

(22)

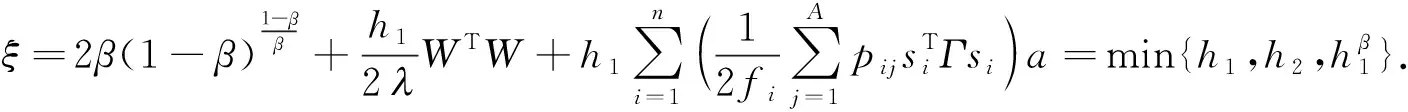
引用引理2，根据引理1，推导得以下结果：

(23)

(24)

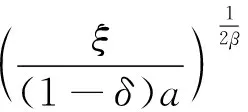
3 仿 真

该部分将对LQR控制和本文提出的模糊有限时间稳定补偿控制这两种控制方法进行参数的对照分析，模拟不同的执行器失效情况，验证其有效性.采用的特殊例子是一个三层建筑，每层有两个执行器，地面加速度假设是1940年埃尔森特罗地震的记录.

3.1 系统参数

模糊逻辑系统和控制器的隶属度函数设计如下：

提出的控制参数如下：

LQR(线性二次调节器)控制的R和Q选择如下：

其中，初始条件为

3.2 实例

假设每层各有一个执行器在3 s后发生部分失效，其参数设置见表1.

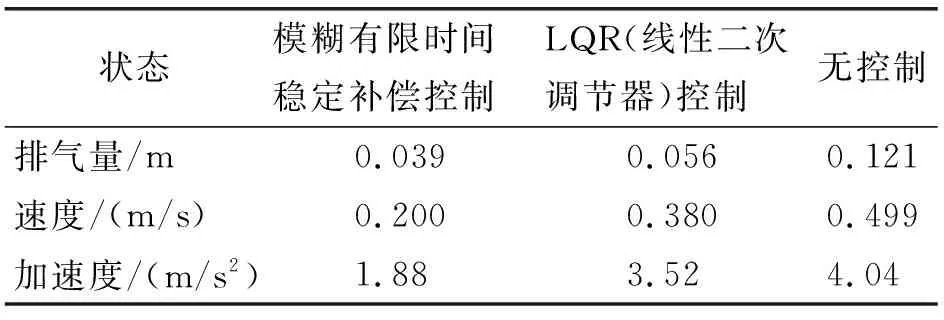
表1 该实例下的最大位移、速度和加速度Table 1 Maximum displacement, velocity and acceleration

由表1可知，在遭受部分失效的情况下，本文方法对建筑物相关地面位移的抑制率约为67.7%，高于LQR控制的53.7%.相应地，该方法下最大速度和加速度明显降低了60%和53.4%.

3.3 仿真图部分

从仿真图2～图4可见，分别采用LQR控制和所提出的控制方法，得到了在部分失效情况下的位移、速度、加速度响应.在图5中，给出了LQR(线性二次调节器)控制与所提出方法的控制力对比.从图6～图7可见，每个执行器的控制输出，分别为本文所提方法及LQR控制下的控制力.

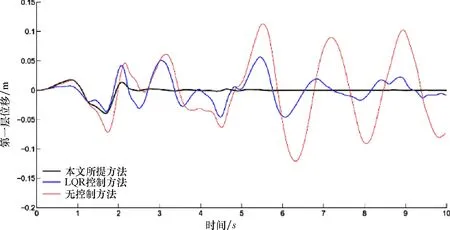
图2 示例中的位移Fig.2 Displacement in example

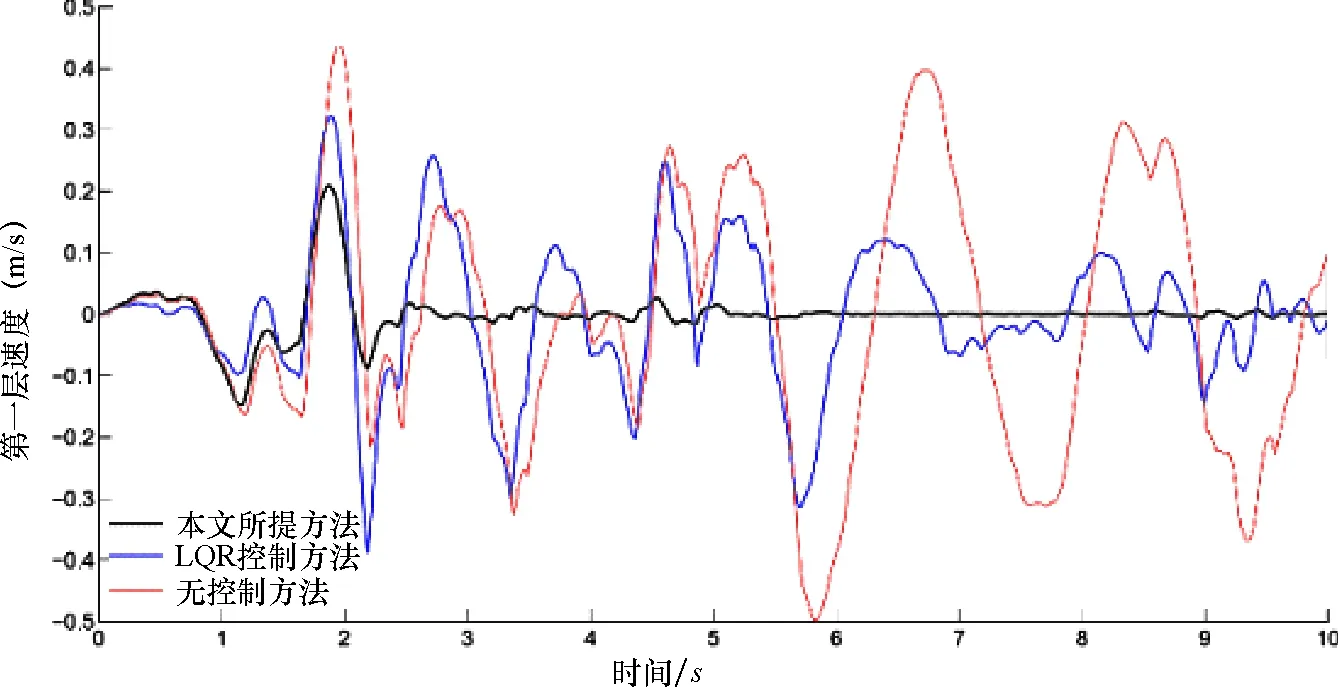
图3 示例中的速度Fig.3 Velocity in example

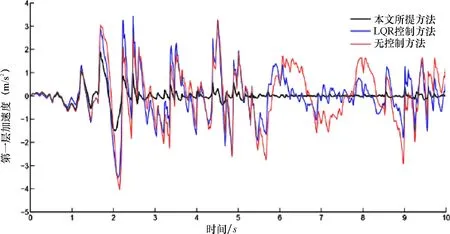
图4 示例中的加速度Fig.4 Acceleration in example

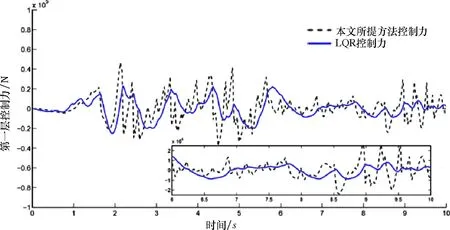
图5 示例中的控制力Fig.5 Controlling force in example

图6 本文提出控制方法下的控制力1和控制力2Fig.6 Force 1 and force 2 for proposed control method

图7 LQR控制下的控制力1和控制力2Fig.7 Force 1 and force 2 for LQR

仿真结果表明，虽然LQR和所提出的控制方法都能有效地抑制建筑结构系统的振动，但是所提出的控制方法比LQR控制更有效，特别是在不同执行器失效的影响下.同时，该方法可以保证层间位移在有限时间内保持在较小的范围内.因此，模糊有限时间稳定补偿控制方法是比较有效的，特别是在执行器失效的情况下.

4 结 论

本文研究了不确定执行器失效情况下的建筑结构非线性控制系统模型，设计出一种建筑结构系统在执行器失效情况下的模糊有限时间稳定振动补偿控制方法，能够保证在地震波作用下，建筑结构系统在有限时间内保持稳定.具体工作如下：

(1)将不确定地震波视为控制系统中的未知非线性项，用模糊自适应方法逼近.

(2)针对执行器失效的问题，结合自适应控制理论，提出了一种自适应故障补偿方法.

(3)结合补偿方法，设计了有限时间主动振动控制来抑制建筑物结构的振动.

(4)稳定性分析和仿真表明，本文方法能保证建筑结构在执行机构失效的情况下，所有状态都是有界的，并且在有限时间内保持稳定.