若干新的s-偶图的Ramsey数
杨 洪, 吴 璞, 邓 飞
(1. 成都大学 信息科学与工程学院, 四川 成都 610106; 2. 广州大学 计算科技研究院, 广东 广州 510006; 3. 成都理工大学 信息科学与技术学院, 四川 成都 610059)
本文只考虑没有重边或环的图.对于图G=(V,E),用V(G)和E(G)分别表示图G的顶点集和边集.一个分类数为m和n的完全偶图可以用Km,n来表示.更多图论的概念和符号请参考文献[1].Erdõs等[2]在1978年开始了边Ramsey数的研究,后来Faudree等[3]、Lortz等[4]和Pikhurko等[5-6]继续这一研究工作.
对于正整数s,以及两个偶图G和H,s-偶图Ramsey数BRs(G,H)是一个最小正整数t,使得每一个Ks,t的2-边着色都含有1色的图G或者含有2色的图H.
文献[7-9]提出了s-偶图Ramsey数的概念,文献[9]得到了关于K2,3和K3,3的s-偶图Ramsey数对于s≤7的一些精确值.最近,Wan等[10]应用一些计算技术,确定出了K2,3和K3,3的2色s-偶图Ramsey数对于s≥8的一些精确值.致力于图论算法研究的基础上[11-12],本文提出了一个新的整数线性规划模型,对其他类型的完全偶图,计算出了双色s-偶图Ramsey数的精确值.实验结果表明,该模型比文献[10]提出的模型更加高效.利用该模型,成功地确定了许多个新的s-偶图Ramsey数的精确值.
1 计算技术
对于完全偶图Ks,t,Ks1,t1和Ks2,t2,建立一个新的线性规划模型,以确定是否存在一个Ks,t的2-边着色方案,使得在该方案中既不含1色的Ks1,t1,也不含2色的Ks2,t2.
1.1 以前的工作
文献[10]提出了一种计算双色s-偶图Ramsey数的整数线性规划(ILP)方法.为了保持论文的独立性,将模型重述如下.
设Ks,t的顶点集是A∪B,其中A={a1,a2,…,as},B={b1,b2,…,bt},且A和B都是独立集.对每一条边{u,v}(u∈A,v∈B),引入布尔变量xu,v,c(1≤c≤2),且xu,v,c=1当且仅当{u,v}着色c.于是,对任意uv∈E(Ks,t),有
xu,v,1+xu,v,2=1
(1)
对每个Ks,t中的K2,3,不妨设顶点分别为a1,a2,b1,b2,b3,有
xa1,b1,1+xa1,b2,1+xa1,b3,1+xa2,b1,1+xa2,b2,1+xa2,b3,1≤5
(2)
对每个Ks,t中的K3,3,不妨设顶点分别为a1,a2,a3,b1,b2,b3,有
(3)
对于给定的正整数s和t,如果不存在满足约束条件(1)(2)(3)的解,那么就有BRs(K2,3,K3,3)≤t;否则就有BRs(K2,3,K3,3)≥t+1.利用上述的整数线性规划模型,成功地求出了BRs(K2,3,K3,3)的所有情形.
1.2 新线性规划模型
对于某些阶数较大的偶图,1.1小节中的整数线性规划(ILP)模型未必能在合理的时间内求解.下面,对较大的图,引入一个新的ILP模型来计算双色s-偶图Ramsey数的精确值,描述如下.
假设完全偶图Ks,t的顶点集是A∪B,其中A={a1,a2,…,as}.设G是Ks,t的一个子图,u,v是正整数,且
Z2={0,1},
y=(y1,y2,…,ys)∈Z2×Z2×…×Z2,
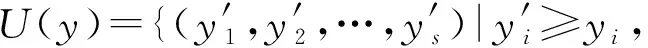
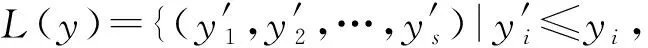
Xy(G)={v|v∈B,v∈NG(ai)对任意yi=1,且v∉NG(ai)对任意yi=0},
定理设Ks,t是一个完全偶图,对于整数s1,t1,s2及t2,存在一个Ks,t的2-边着色方案使得在该方案中既不含1色的Ks1,t1也不含2色的Ks2,t2,当且仅当存在一个Ks,t的子图G满足Ds1,t1(G)=∅及Ms2,t2(G)=∅.
证明设完全偶图Ks,t的顶点集是A∪B,其中A={a1,a2,…,as}.现在假设存在一个Ks,t的2-边着色方案使得方案中既不含1色的Ks1,t1也不含2色的Ks2,t2.将Ks,t中的1色导出的子图记为G.先考虑以下两种情形:
情形1:Ds1,t1(G)≠∅.
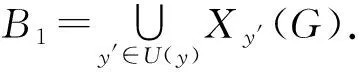
情形2:Ms1,t1(G)≠∅.
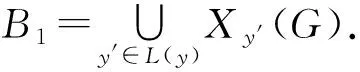
如果存在满足Ds1,t1(G)=∅,Ms1,t1(G)=∅ 的Ks2,t2的子图G,那么就将G中的所有边着颜色1,其余边都着颜色2.现考虑如下两种情形:
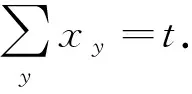
现将条件Ds1,t1(G)=∅,Ms1,t1(G)=∅应用到如下约束中:
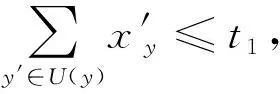
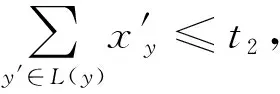
因此,提出一个新的ILP模型,其约束条件如下所示:
(4)
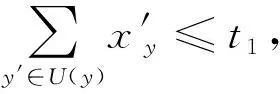
(5)
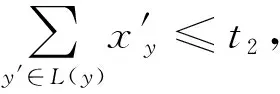
(6)
于是可得,存在满足Ds1,t1(G)=∅,Ms1,t1(G)=∅ 的Ks,t的子图G,当且仅当存在一个满足约束条件(4)(5)(6)的解.由定理可知,存在一个Ks,t的2-边着色方案满足既不含有1色的图Ks1,t1也不含有2色的图Ks2,t2,当且仅当存在一个满足约束条件(4)(5)(6)的解.
2 计算结果
如表1所示,文献[9]和文献[10]确定了BRs(K2,3,K3,3)的值.但是,欲求BRs(K3,3,K3,3)的值或其他偶图Ramsey数的值,用文献[10]提供的ILP模型仍然很难确定.

表1 BRs(K2,3,K3,3)的精确值Table 1 Exact values of BRs(K2,3,K3,3)
为了验证新ILP模型的有效性,在2.66 GHz的CPU环境下利用软件Gurobi[8],分别用两种ILP模型求解BRs(K2,3,K3,3)的值,通过实例将这两个模型进行比较.设文献[10]中原有的ILP模型和本文中的新ILP模型分别用old ILP和new ILP来表示.实验结果表明,对任意的s∈{5,6,…,10},都无法在1 h内通过old ILP模型求出相应的精确值.可是,当s=5,6时,在0.01 s内通过new ILP模型成功地求出了相应的精确值.当s=19,t=23时,仅用5.35 s就通过new ILP模型成功地求出了相应的精确值.而且,通过new ILP模型成功地求出了55个新的精确值,结果如表2~表11所示.
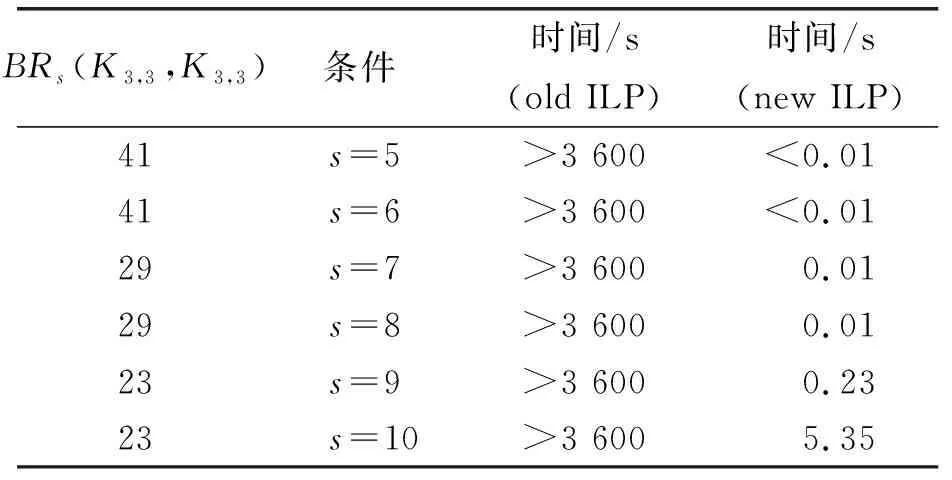
表2 BRs(K3,3,K3,3)的精确值Table 2 Exact values of BRs(K3,3,K3,3)

表3 BRs(K2,4,K3,3)的精确值Table 3 Exact values of BRs(K2,4,K3,3)

表4 BRs(K2,5,K3,3)的精确值Table 4 Exact values of BRs(K2,5,K3,3)

表5 BRs(K2,6,K3,3)的精确值Table 5 Exact values of BRs(K2,6,K3,3)

表6 BRs(K2,7,K3,3)的精确值Table 6 Exact values of BRs(K2,7,K3,3)

表7 BRs(K3,4,K3,3)的精确值Table 7 Exact values of BRs(K3,4,K3,3)

表8 BRs(K3,5,K3,3)的精确值Table 8 Exact values of BRs(K3,5,K3,3)

表9 BRs(K2,3,K3,4)的精确值Table 9 Exact values of BRs(K2,3,K3,4)

表10 BRs(K2,4,K3,4)的精确值Table 10 Exact values of BRs(K2,4,K3,4)

表11 BRs(K2,5,K3,4)的精确值Table 11 Exact values of BRs(K2,5,K3,4)
3 结束语
在文献[9]中,Bi等首先开始研究了当s≤7时K2,3和K3,3的s-偶图Ramsey数的情况.文献[10]提出一些计算技术来获得了K2,3和K3,3的s-偶图Ramsey数的其他所有情形.然而,利用文献[10]中的方法,无法在1 h以内求出当s≥5时的BRs(K3,3,K3,3).本文提出了一个新的ILP模型,能求出当5≤s≤10时的BRs(K3,3,K3,3)的精确值.而且,对其它多种组合下的完全偶图情形,通过新ILP模型求出了多达55个2色s-偶图Ramsey数的精确值.

