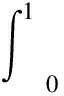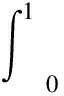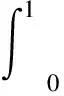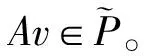一类含参数的Caputo型分数阶微分方程正解的唯一性
张 金, 汪 娜
(上海应用技术大学 理学院,上海 201418)
相较于整数阶微分方程,分数阶微分方程有较大的优势。分数阶微分方程对于事物变化规律的描述更为灵活与准确。因此,在实际生活中分数阶微分方程应用广泛。但是由于分数阶微分方程的初值较为复杂,它们具备的某些物理意义也没有被普遍认可,以至于分数阶微分方程理论的发展依然处于起步阶段。分数阶微分方程边值问题中对导数有限制,这对其研究造成了一定的难度。但由于其广泛的实际应用价值、重要的理论意义以及开阔的研究前景,分数阶微分方程理论成为当下众多学者研究的热点[1-4]。
早在300年前,分数阶微积分就已被提出。分数阶微分方程的研究需要综合运用不同数学知识, 如实变函数、复变函数、积分变换、泛函分析、线性代数等。因此分数阶微分方程的研究具有一定的难度和综合性[5-6]。此外, 分数阶微分方程与其他多种学科的联系逐渐紧密, 分数阶微分方程在运用于不同领域的同时, 其内容也变得越来越丰富。众多学者对分数阶微分方程及其应用进行了不少研究, 收获颇丰。
分数阶微分方程在数学领域的研究最多,冯子鑫等[7]研究了一类无穷区间上具有积分边界条件的分数阶微分方程边值问题。作者先构造格林函数, 讨论其相关性质, 再利用压缩映象原理及单调迭代法, 研究此类边值问题正解的存在性, 建立了若干正解存在的定理。在数值计算领域,刘宝强[8]基于变分迭代和DNA序列运算, 设计了一种改进的分数阶微分方程数值解析算法优化了算法的性能。在复杂流体研究领域,潘明阳[9]首次建立了含有空间分数阶导数的流动控制方程的相似变换公式, 研究了壁面射流和斗板绕流问题。
当前主要的分数阶导数的类型有Caputo型、Riesz型、Riemann-Liouville型等分数阶导数。其中Caputo型和Riemann-Liouville型分数阶导数因为有广阔应用背景且计算相对简便, 所以应用更为广泛。目前分数阶微分方程理论的研究逐年递增, 其中关于分数阶微分方程解的存在性的研究最多, 而不动点定理是研究分数阶微分方程边值问题解存在的常用工具。但关于Caputo型分数阶微分方程复杂边值问题正解的存在性研究却较少, 其原因在于:① Caputo型分数阶微分方程边值问题中对锥和算子的构造相对比较困难; ② 适合算子拉伸、压缩的不等式证明, 以及算子在拉伸或压缩过程中体现其对正解存在性的影响的结果不易得到。
近期,Zhai等[10]研究了含参数的非线性Caputo型分数阶微分方程边值问题:
(1)
式中:1<α≤2,0≤ξ≤η≤1且0≤μ1,μ2≤1,λ>0是一个参数;f(t,x):[0,1]×R+→R+是连续的,x对于t∈[0,1]是增函数。通过运用凹算子不动点定理,得到该问题存在唯一正解的充分条件。
贾建梅等[11]考虑了带积分边界条件的分数阶微分方程的边值问题:
(2)

受文献[10-11]的启发,本文研究一类含参数的Caputo型分数阶微分方程
(3)
式中:n+1<α≤n+2且n∈N,λ>0是一个参数;p≥0,q≥0,p+q≠0;0<μ 本文将运用凹算子不动点定理得到边值问题式(3)存在唯一正解的存在定理。 定义1函数φ:[0,+∞)→R的α阶Riemann-Liouville型积分定义为[12] 其中α>0,等式右边在(0,+∞)上是逐点定义的。 Caputo型分数阶微分定义可用Riemann-Liouville型积分算子Iα给出如下定义: 定义2函数φ:[0,+∞)→R的α阶Caputo型微分定义为[12] cDαφ(x)=In-αDnφ(x)= 其中α>0;[α]是指取实数α的整数部分;Γ函数对于n∈N,具有性质Γ(n)=(n-1)!。 定义3设D是E中的一个凸子集[13]。如果算子A:D→E满足 A(tx+(1-t)y)≥tAx+(1-t)Ay,x,y∈D,t∈[0,1] 则称A是凹算子。 定义4设是实Banach空间E中的锥并且e∈P/θ。集合Ee={x∈E:存在λ>0,使得 -λe≤x≤λe},且 ‖x‖e=inf{λ>0: -λe≤x≤λe}, ∀x∈Ee. 易见Ee是范数为‖·‖e的赋范线性空间,其中 ‖x‖e称为元素x的e—范数。 引理3[15]设锥P是正规的,则以下结论成立: (1)Ee是具有e—范数的Banach空间,则存在常数m>0使得m‖v‖e,∀v∈Ee; (2)Pe=Ee∩P是Ee中的正规锥,且Pe={v∈Ee:存在τ=τ(v)>0使得v≥τe}。 引理4[16]设P是正规锥且算子A:P→P是凹的。假设Aθ≫θ。则下列结论成立: (1)存在0<λ≪∞使得方程 v=λAv (4) 在P中存在唯一解v(λ),0≤λ<λ*;当λ≥λ*,则方程(4)在P中无解。 (2)对任意v0∈P,设v0(λ)=v0,vn(λ)=Avn-1(λ),n=1,2,…,则当n→∞时,对0≤λ<λ*,有vn(λ)→v(λ); (3)v(·):[0,λ*)→P连续且强递增(即,0≤λ1<λ2<λ*⟹v(λ1)≪v(λ2))。而且对0≤λ<λ*,有v(tλ)≤tv(λ),0≤t≤1; (4)若存在v0∈P且λ0>0使得λ0Av0≤v0,则λ*>λ0。 引理5[16]若A:P→P是凹的,则A是递增的。 引理6[16]设P是正规体锥且算子A:P0→P0是递增的。若存在常数0 A(tv)≥trAv, ∀v∈P0, 0 记vλ是方程Av=λv(λ>0)在P0中的唯一解,则 (1)vλ是强递减的(即,0≤λ1<λ2<λ*⟹vλ1≫vλ2); (2)vλ连续(λ→λ0(λ0>0)⟹‖vλ-vλ0‖→0); (3)limλ→∞‖vλ‖=0, limλ→0+‖vλ‖=∞。 引理7设φ(x)∈C[0,1];n+1<α≤n+2且n∈N;p≥0,q≥0,p+q≠0;0<μ (5) 其中ψ(t)=(n+1)p+n(n+1)q-μξn+1(1-t)。 证明由定义1及引理2,(5)中方程cΔαv(x)+h(x)=0等价于 (6) 由(4)中条件v(0)=v′(0)=…=v(n-1)(0)=v(n+1)(0)=0,得 (7) (8) (9) (10) (11) 将式(11)代入式(7)得 (12) 当0≤x<ξ≤1时,有 当0≤ξ 故引理3得证。 引理8设n+1<α (3)ψ(t)>0,且ψ(t)在[0,1]上为增函数; (4)G(x,t)≥0,∀x∈(0,1)。 证明当0≤t≤x≤ξ≤1时,有 α(α-1)(n+1)qxn(1-t)α-2-(n+1)μxn(ξ-t)α}= (α2-α)(n+1)qxn(1-t)α-2t-(n-1)μxnCα(1-t)α-1}≥ 且 α(α-1)(n+1)qxn(1-t)α-2-(n+1)μxn(ξ-t)α}= (n+1)μxn(ξ-t)α+(α2-α)(n+1)qxn(1-t)α-2t}≤ 当0≤ξ≤t≤x≤1时, (α-1)(n+1)qxn(1-t)α-1+(α-1)(n+1)qxn(1-t)α-2t}≥ 且 (α-1)(n+1)qxn(1-t)α-1+(α-1)(n+1)qxn(1-t)α-2t}≤ 当0≤x≤t≤ξ≤1时,有 (n+1)μxnξα(1-t)α+(α2-α)(n+1)qxn(1-t)α-2t}≥ (n+1)μxnξn+1(1-t)α+(α2-α)(n+1)qxn(1-t)α-2t}≥ 且 (n+1)μxn(ξ-t)α+(α2-α)(n+1)qxn(1-t)α-2t}≤ 当0≤ξ≤x≤t≤1时,有 且 因此引理8(1)-(2)得证。由ψ(t)的表达式容易证明引理4(3)成立。由引理8(1)易见(4)成立。综上引理8得证。 定理1假设f(x,·)是凹的,且存在常数α,β>0使得 f(x,0)≥0,f(x,1)≤β, ∀x∈[0,1] (13) 和 f(x,v)≤vf(x,1)-(v-1)f(x,0)≤βv 故对v∈P,有1 预备知识与研究工具
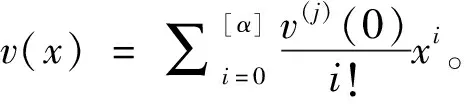
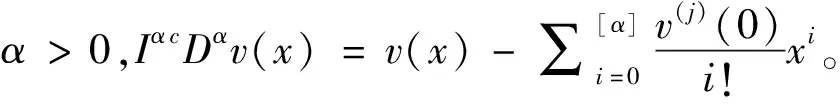
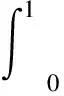
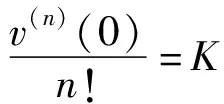




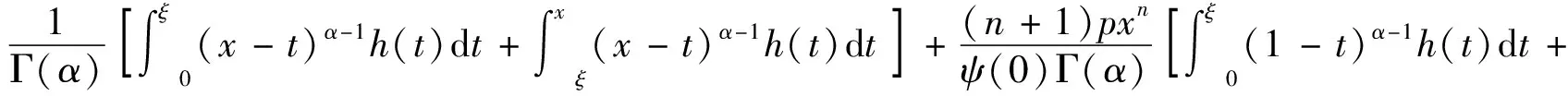
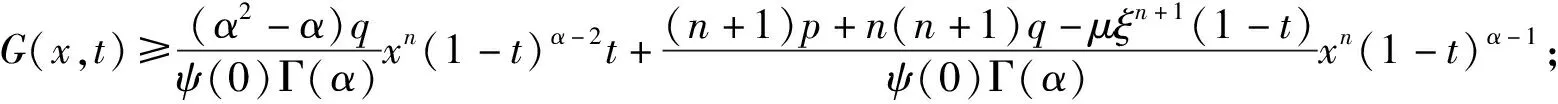



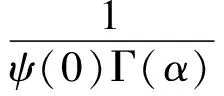
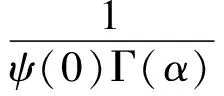



2 正解存在性