轴承摩擦磨损对柔性支承转子动力响应特性的影响

吴庭苇

(粒子输运与富集技术国防科技重点实验室，天津 300180)

柔性支承转子的轴承由轴和窝组成，具有支承转子和连接转子与阻尼装置的功能。在研究柔性支承转子的动力学问题时，通常在建立模型时将轴简化为连接转子下端与阻尼上端的1根弹簧，假设轴和窝之间是刚性连接的，无相对滑动或摩擦。这种传统的轴承简化模型无法对轴承的运动状态和配合方式进行理论研究，导致轴承设计缺乏理论基础。此外，在工程和试验中均发现，运转后转子的轴端部球面和窝的球面上存在磨痕，说明轴和窝之间存在相对运动和摩擦。传统模型不能对这些现象和作用机理进行具体分析，需对转子模型中的轴承简化模型进行改进，建立轴承非刚性连接的转子模型是有效的改进途径。

作为柔性支承转子中旋转件与静止件唯一的接触点，轴承的相对运动和摩擦对转子动力响应特性有直接影响，研究其作用机理和影响因素可为柔性支承转子的轴承优化设计和转子失效原因分析提供理论依据。

目前，已有学者对柔性支承转子的轴承磨损性能开展了相关试验研究。苏荔[1-2]建立了磨损性能试验装置，从耐磨性能和减磨性能2个方面对轴承摩擦副的磨损性能进行了研究。谢军[3]采用高速摩擦磨损专用试验机，进行了宝石轴承的摩擦磨损试验，得出了性能优良的摩擦学匹配设计方案。蒋书运[4]采用Falex型摩擦磨损试验机考察了T8钢/Al2O3陶瓷摩擦副在3种油性剂与极压抗磨剂作用下的摩擦学性能。

但柔性支承转子的轴承相对运动和摩擦对柔性支承转子动力响应的影响方面研究较少。李正光等[5]运用数值方法计算了转子在稳态和非稳态下的振动响应，并测量了实际运行时转子的振动特征，对比测量结果与理论分析结果表明，建立转子的动力学模型并采用数值方法进行求解能有效对转子的动力学行为进行分析。杨光明等[6-7]通过实验测量了轴与窝之间的相对位移，并结合理论分析说明轴与窝之间微小的相对运动会对转子动力学行为产生一定影响。

本文以柔性支承转子的轴承摩擦磨损对转子动力响应特性的影响研究为切入点，通过对运动状态下的轴承进行受力特性分析，建立轴承非刚性连接的转子模型，数值计算并分析转子在轴承摩擦磨损影响下的动力响应特性，分析轴承摩擦磨损对转子失效模式和释放最大能量的影响。

1 理论模型

1.1 物理模型

1) 转子模型及轴承非刚性连接力学模型

建立柔性支承转子模型，首先对转子进行如下简化与假设：(1) 转子是亚临界的，近似地视为刚体；(2) 上支承对转子在竖直方向上具有磁拉力作用，考虑其径向刚度对转子系统的影响；(3) 下阻尼件仅做平动运动而不能转动；(4) 转子做横向微幅振动。

根据基本假设，转子的力学模型可简化成图1所示系统。其中，磁钢的径向刚度为k1；转子的质量为M；轴的径向刚度为k2；阻尼装置的刚度、质量和阻尼分别为k3、m3、c3。轴承由轴和窝组成，轴即为图中的弹簧k2，窝固结于阻尼装置的顶部，轴与窝示意图如图2所示。

设轴的半径为rz，宝石轴承窝半径为rw，系统静止时，轴的轴线与z轴重合。转子运转时，轴和宝石轴承窝之间发生相对移动，xOz平面上的受力分析如图2所示。轴直径很小，可忽略力矩的影响，为简化计算，将轴所受的轴向承载力P移到轴球面与窝的接触点。假设轴仅在B点与窝接触，其中fz为xOz平面上的滑动摩擦力，N为窝对轴产生的法向反力，α为法向反力方向与水平方向的夹角。

图1 转子-支承系统力学模型Fig.1 Model of rotor-bearing system

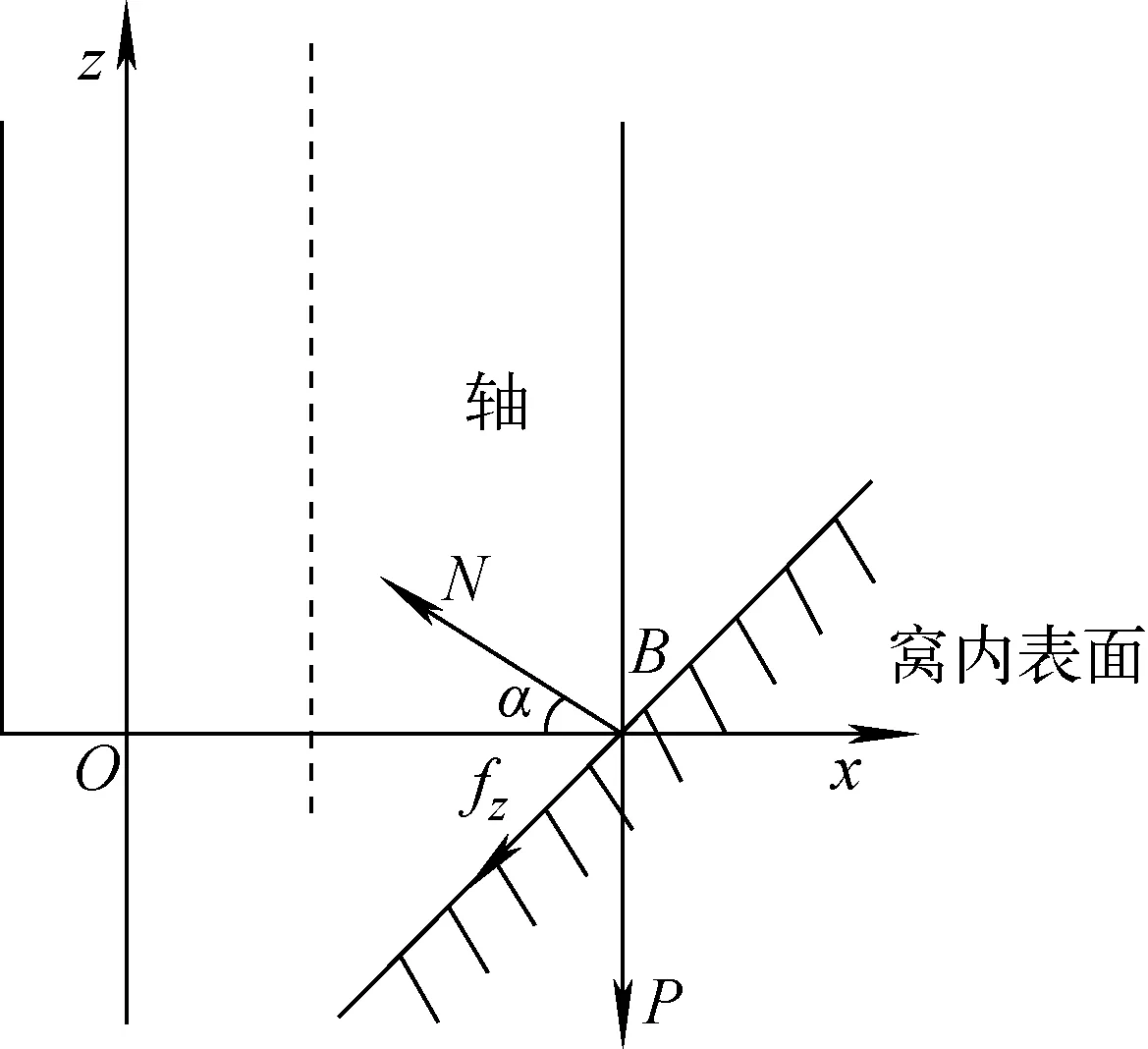
图2 xOz平面轴受力示意图Fig.2 Diagram of bearing forces in xOz plane

图2中的α可表示为：

(1)

其中，Δr为轴与窝在水平方向上的相对位移。

根据受力分析可知转子在运行过程中，竖直方向上所受合力为0，fz等于正压力与摩擦系数乘积，得出轴所受法向反力N与fz和正压力P之间的关系，如下式所示。

(2)

图3为轴与窝在xOy平面上的受力分析，其中Ff为轴在旋转方向上所受的滑动摩擦力，NxOy为轴所受法向反力在xOy平面上的分量，同理，fxOy为滑动摩擦力在xOy平面上的分量。

将NxOy、fxOy进行矢量合成，得到轴在xOy平面上所受的径向合力，假设轴旋转所受的周向滑动摩擦力为干摩擦形式，则周向滑动摩擦力Ff为径向力与摩擦系数的乘积，如下式所示。

(3)

Ff=μ(NxOy+fxOy)

(4)

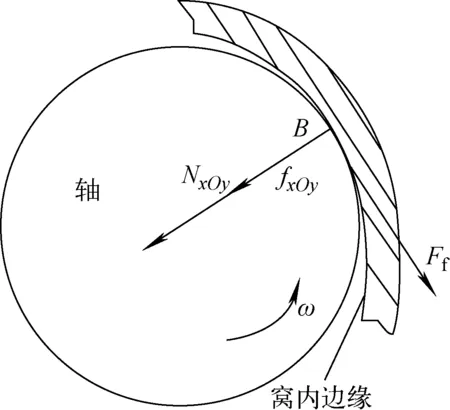
图3 xOy平面轴受力示意图Fig.3 Diagram of bearing forces in xOy plane

将轴所受的力分解到x、y方向上，并分别合成，得到轴在x、y方向上所受的合力Fx、Fy。

将轴所受的外力代入系统运动方程中，即可计算非刚性连接系统的转子动力响应。按照上述力学模型，在运用数值方法求解转子动力响应时，每向前推进1个时间步长，需对位移系数矩阵进行1次求逆计算。然而，轴的自身质量与转子质量相比为1个极其小量，若将轴作为1个广义坐标引入系统中，会造成位移系数矩阵接近奇异化，求逆计算将变得异常困难，导致很难求得非刚性连接转子-支承系统的动力响应。

2) 轴-窝连接刚度模型

为解决上述问题，本文引入连接刚度kl，将轴与窝之间的相互作用力Fx、Fy等效为连接刚度与二者相对位移的乘积。连接刚度不是一个常量，与轴在窝中的相对位置有关，因此该系统中的kl为非线性刚度，将轴在xOy平面上所受的外力Fx、Fy分别对x、y方向上的位移进行求导，即可得到任意时刻的连接刚度klx、kly。根据轴与窝的运动特性可知，连接刚度与轴为串联关系，如图4所示。

引入连接刚度后，转子与阻尼器连接的等效刚度kz如下式所示：

(5)

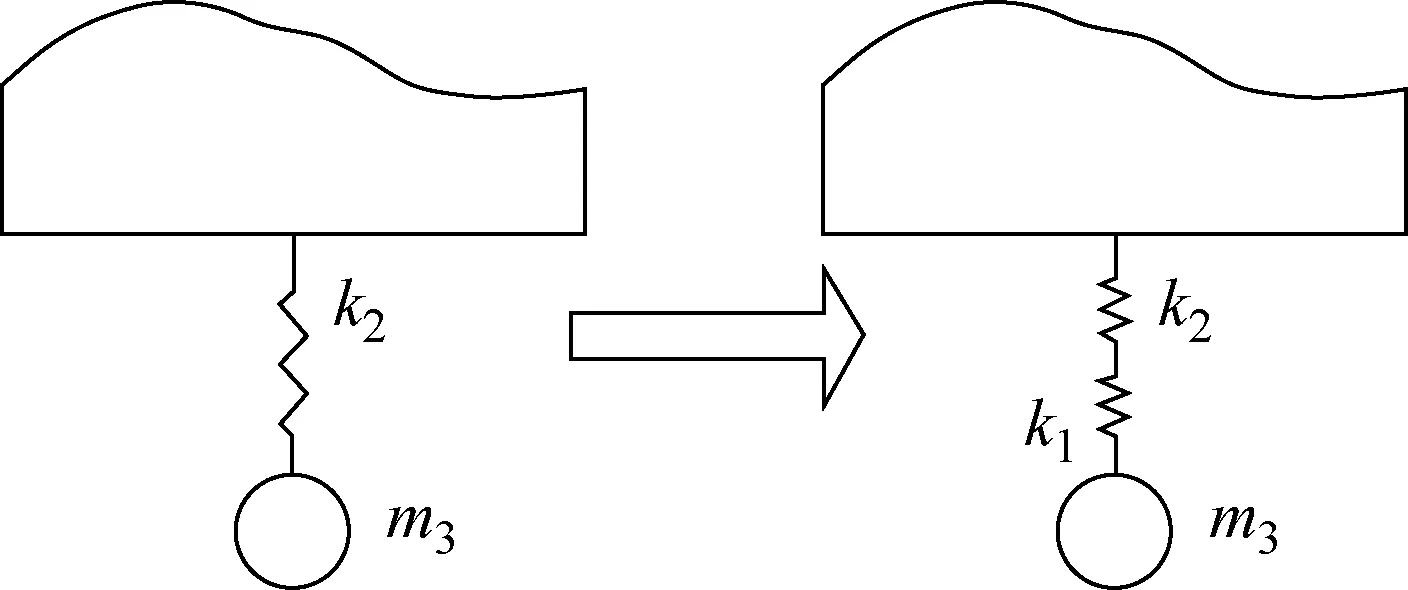
图4 轴承连接刚度示意图Fig.4 Diagram of bearing connection stiffness

通过引入连接刚度和以上一系列的处理，即可将轴作为一个弹性连接件引入转子模型，转子下端通过轴和轴承以非线性连接方式与阻尼器相连，解决了计算过程中求逆运算的困难，从而能运用数值计算方法对转子的动力响应进行计算。

1.2 数学模型

对于上述轴承非刚性连接的转子力学模型，采用拉格朗日方法[8]建立其对应的数学模型。计算转子系统的动能、势能、耗散能，分别代入拉格朗日方程，即可得到转子-支承系统的运动微分方程：

(6)

其中：k1为上支承的径向刚度；k3、m3、c3分别为阻尼器的刚度、质量和阻尼；M为转子的质量，l为长度，ls为转子质心与转子下端在z方向上的距离；Jt为转子的赤道转动惯量；Jp为转子的极转动惯量；x1、y1为转子上端位移，x2、y2为转子下端位移，x3、y3为阻尼体上端，即窝的位移；Qx1、Qy1为转子上端所受的外激励，Qx2、Qy2为转子下端所受的外激励，Qx3、Qy3为阻尼体上端所受的外激励。

2 计算方法及研究方案

2.1 计算方法

本文采用四阶Runge-Kutta方法[9]对转子-支承系统的运动微分方程进行数值求解。

将式(6)改写为矩阵形式并进行适当变换得到式(7)，其中M、C、K分别为质量、阻尼、刚度矩阵，r为坐标矩阵。

(7)

为了使用Runge-Kutta方法进行求解，将式(7)变换至适当形式，如式(8)、(9)所示：

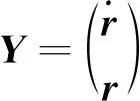
(8)

(9)

假设转子-支承系统初始时刻t0时的位移值为Y0，在[t0，t1]时间段内应用以下四阶Runge-Kutta迭代公式(式(10))，计算在等距节点tn=t0+nh(n=1，2，…，N)上的数值解Yn，即转子-支承系统的动力响应值。

(10)

转子动力响应具有时域特性和频域特性，运用Runge-Kutta方法计算得到转子的时域动力响应后，即可得到其时域特性。在频域特性分析方面，本文采用快速傅里叶变换方法[10]对转子的时域动力响应进行计算，即可得到转子的频域响应特性。

式(11)、(12)为快速傅里叶变换公式。

(11)

ωN=e-2πi/N

(12)

式中：X(k)为频域响应；Y(j)为计算得到的时域响应Yn；i、j、k均为计算序数，取值范围为1～N。

2.2 研究方案

为分析轴承摩擦磨损程度等因素对转子动力学响应特性的影响，分析转子的运动特性，计算并分析轴承摩擦磨损对转子失效模式及其最大失效能量的影响。本文以柔性支承转子为研究对象，运用本文的建模方法建立轴承非刚性连接的柔性支承转子数学模型，运用数值方法计算转子的动力响应。研究方案如下：1) 计算不同轴承摩擦磨损程度下转子的动力响应，分析其对转子动力响应的影响；2) 计算并分析转子在轴承严重摩擦磨损状态下的动力响应特性；3) 计算轴承摩擦磨损导致转子出现进动失效时转子释放的最大能量，分析轴承磨损导致转子进动失效对释放能量的影响。

2.3 轴承摩擦磨损状态模拟方法

为研究不同轴承摩擦磨损程度对转子动力响应的影响，本文根据《轴球面磨损等级评定》[11]对轴的摩擦磨损进行分类并划分等级。《轴球面磨损等级评定》根据轴球面表面摩擦磨损情况，给出了5种磨损外形形貌特点(表1)。

表1 轴端部球面磨损形式Table 1 Wear pattern of bearing sphere

轴磨损外形及测量参数示于图5。

为进一步区分磨损等级，对相同磨损外形形貌，又以不同磨痕宽度表示磨损等级(表2)。

为研究轴球面表面摩擦磨损外形为H、Z、Q、M的4种情况，通过逐渐增大径向摩擦系数来模拟计算不同磨损程度对转子-支承系统的影响。为研究轴球面表面摩擦磨损外形D，通过将接触区域与非接触区域设为不同的径向摩擦系数来模拟计算不同磨损程度对转子-支承系统的影响。

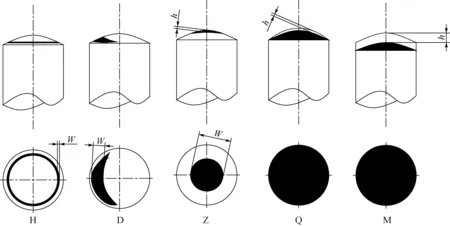
图5 轴磨损外形及测量参数Fig.5 Bearing wear profile and measurement parameter

等级磨损宽度HDZQM说明ⅠW≤0.5 mmW≤0.5 mmW≤1 mm无无轻微Ⅱ0.5 mm2.5 mmW>3 mmW>4 mm,或h>0.35 mmh>0.25 mm是严重

3 计算结果及分析

3.1 轴承无磨损状态下的转子动力响应

按照柔性支承转子技术条件，轴与窝之间的摩擦系数设计值为0.25，此时轴球面及窝球面无摩擦磨损。采用本文计算方法，计算工作转速为500 s-1下转子的时域响应，通过傅里叶变换，得到转子下端的振幅为0.16 mm，如图6所示。从图6可看出，当轴承无摩擦磨损时，转子以工作转速做稳定的自转运动，无进动。

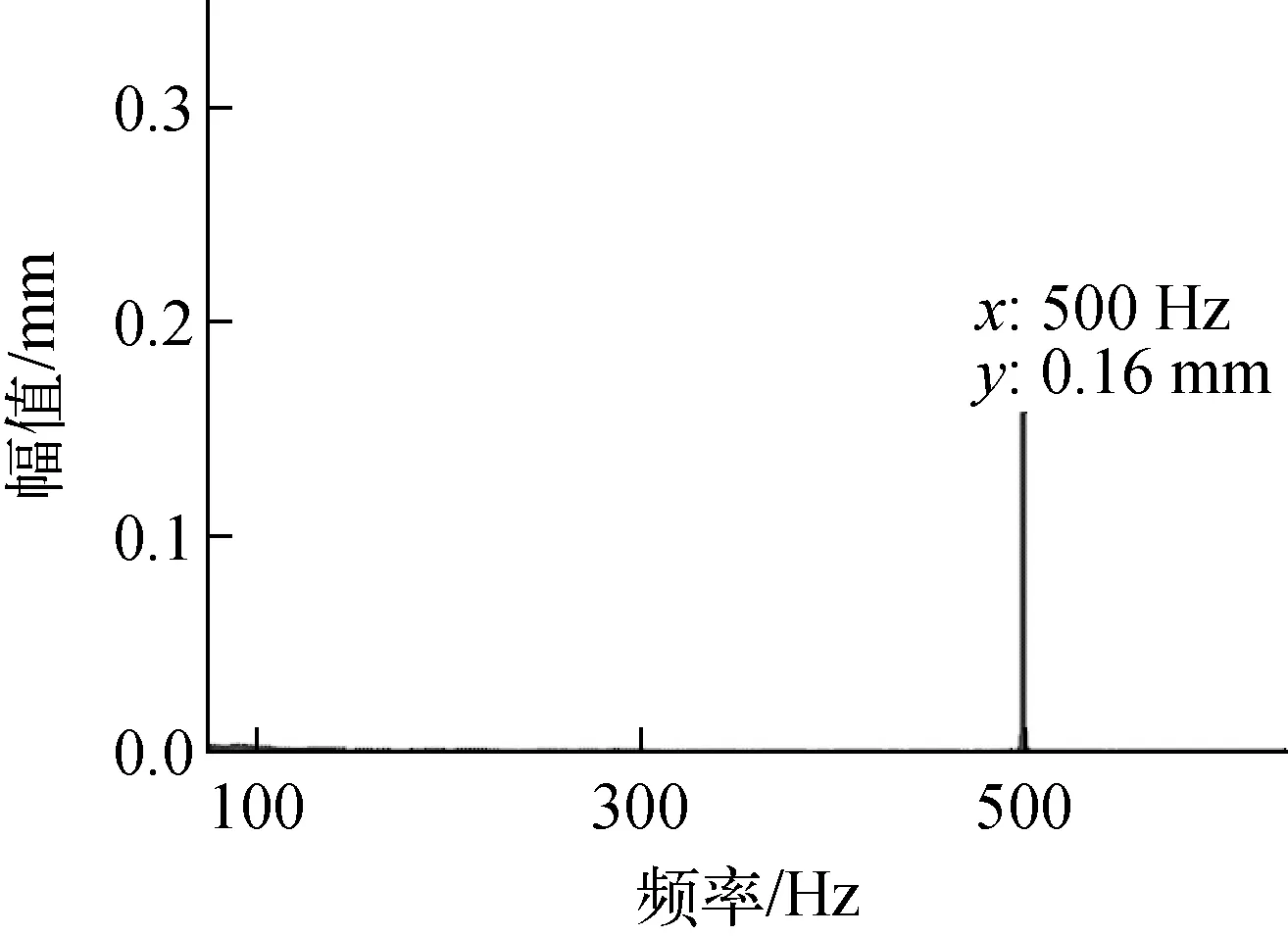
图6 转子下端振幅的幅频特性曲线Fig.6 Amplitude-frequency characteristic curve of rotor lower part

3.2 轴端面磨损程度对转子动力响应的影响

1) 磨损外形为H、Z、Q、M

(1) 不同轴承摩擦磨损程度对转子振幅的影响

柔性支承转子技术条件中，轴与窝之间的摩擦系数设计值为0.25，此时轴球面及窝球面均完好无损。假设磨损等级为Ⅰ级时，摩擦系数为0.5；磨损等级为Ⅱ级时，摩擦系数为0.6；磨损等级为Ⅲ级时，摩擦系数为0.7；磨损等级为Ⅳ级时，摩擦系数为0.8。

采用本文计算方法，计算工作转速为500 s-1下转子的时域响应，得到在轴承不同磨损程度下的转子下端幅值变化曲线，如图7所示。从图7可看出，相比轴承无磨损状态下转子振幅(图6)，随着轴承摩擦磨损严重，轴承摩擦系数不断增大，转子下端的振动幅值也逐渐增大，说明轴承整圈磨损越严重，转子振动越剧烈。

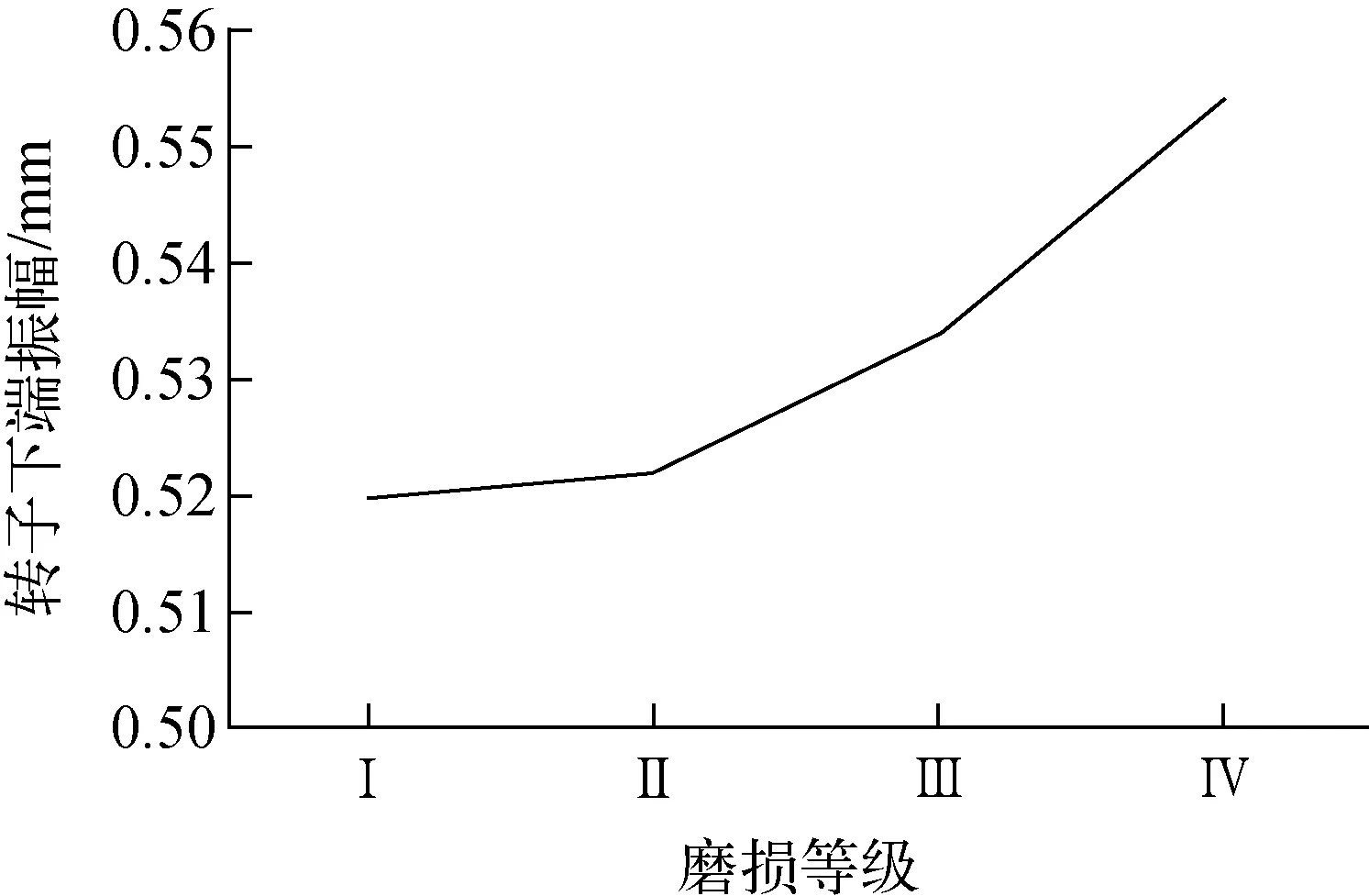
图7 磨损外形为H、Z、Q、M时 转子下端幅值与轴承磨损程度的关系Fig.7 Amplitude of rotor lower part vs. bearing wear degree for wear profiles H, Z, Q and M

(2) 不同轴承摩擦磨损程度对转子进动幅值的影响

采用本文计算方法，计算工作转速为500 s-1下转子的时域响应，通过傅里叶变换，得到在轴承不同磨损程度下的转子下端幅频特性曲线，如图8所示。从图8可看出，相比轴承无磨损状态下转子幅频特性曲线(图6)，当轴承产生整圈摩擦磨损时，不仅转子下端的振动幅值增大，同时伴随着出现了系统二阶进动。当轴承磨损等级为Ⅰ级时，转子二阶进动幅值为0.067 mm；当轴承磨损等级为Ⅱ级时，二阶进动幅值为0.092 mm；当轴承磨损等级为Ⅲ级时，转子二阶进动幅值为0.111 mm；当轴承磨损等级为Ⅳ级时，转子二阶进动幅值为0.14 mm。随着轴承整圈摩擦磨损程度加剧，转子的二阶

图8 磨损外形为H、Z、Q、M时转子在不同轴承磨损程度下的幅频曲线Fig.8 Amplitude-frequency characteristic curve of rotor for different bearing wear degrees for wear profiles H, Z, Q, and M

进动幅值越来越大，存在发散趋势，说明随着轴承磨损严重，转子动力响应特性发生了明显变化。

2) 磨损外形为D

(1) 不同轴承摩擦磨损程度对转子振幅的影响

根据表2中列出的磨损等级Ⅰ～Ⅳ对应的磨损宽度，本文在计算中将磨损宽度分别设为0.5、1、3、4 mm，计算不同磨损程度下转子的动力响应，得到转子下端幅值变化曲线，如图9所示。从图9可看出，随着轴承局部摩擦磨损加剧，转子下端的振动幅值逐渐增大，说明磨损程度越严重，转子振动越剧烈。

(2) 不同轴承摩擦磨损程度对转子进动幅值的影响

采用本文计算方法，计算工作转速为500 s-1下转子的时域响应，通过傅里叶变换，得到在轴承不同磨损程度下的转子下端幅频特性曲线，如图10所示。从图10可看出，相比轴承无磨损状态下转子幅频特性曲线(图6)，当轴承产生局部摩擦磨损时，不仅转子下端的振动幅值增大，同时也伴随着出现了系统二阶进动。当磨损等级为Ⅰ级时，二阶进动幅值为0.055 mm，当磨损等级为Ⅱ级时，二阶进动幅值为0.084 mm，当磨损等级为Ⅲ级时，二阶进动幅值为0.111 mm，当磨损等级为Ⅳ级时，二阶进动幅值为0.15 mm。随着轴承局部磨损越来越严重，磨损区域宽度增大，转子的二阶进动也随之变得更加明显，且存在发散趋势，说明随着轴承磨损变得严重，转子动力响应特性也发生了明显变化。

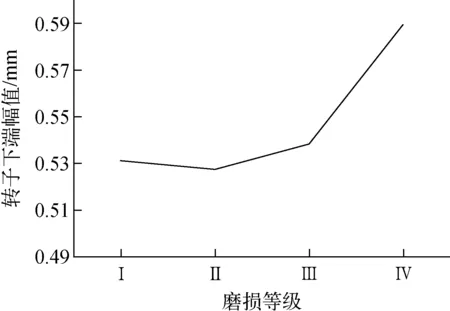
图9 磨损外形为D时转子下端幅值 与磨损程度的关系曲线Fig.9 Amplitude of rotor lower part vs. bearing wear degree for wear profile D

图10 磨损外形为D时转子在不同轴承磨损程度下的幅频曲线Fig.10 Amplitude-frequency characteristic curve of rotor for different bearing wear degrees for wear profile D

3.3 轴承摩擦磨损状态下转子的运动特性

从上述结果可看出：轴承摩擦磨损对转子的动力响应特性产生了明显影响。当轴承出现轻微磨损时，转子振幅增大；随着磨损程度的加重，转子振幅持续增大，并伴随出现转子系统二阶进动，而且进动越来越明显。说明转子系统在轴承摩擦磨损状态下会出现二阶进动，严重时可能导致转子的振幅过大，影响转子稳定运行。

进一步计算分析轴承整圈摩擦磨损达到Ⅳ级以上时，轴承摩擦磨损加剧，转子在出现二阶进动现象的同时，轴承的非线性摩擦运动导致转子产生了拟周期运动(图11)。

图11中，f1=84 Hz为转子二阶进动频率，f2=500 Hz为转子工作频率，f3=f2-f1=416 Hz、f4=f3-3f1=416-3×84=164 Hz、f5=f2-f4=500-164=336 Hz为转子拟周期运动频率[12-15]。该现象说明此时转子的运动状态包含自转、二阶进动以及3种拟周期运动，这5种运动形式叠加，会进一步加剧轴承的摩擦磨损程度。

在实际工程中也曾出现同类现象，对工程中的失效转子进行解体，发现大量转子的轴端部球面上出现了明显磨痕，一些磨损严重的轴甚至被磨短，导致转子下端与电机定子的间隙变小，电子转子盘与电机定子发生了碰磨。在转子强度强化试验中，部分转子出现了二阶进动现象，并最终导致转子失效，对这些失效转子进行解体后同样发现轴端部球面上出现了明显的磨痕。

图11 具有拟周期运动特征的幅频曲线Fig.11 Amplitude-frequency relationship with characteristics of quasi-periodic motion

从以上研究结果可看出，利用本文建立的理论模型，通过增大摩擦系数和磨损宽度等方法模拟不同轴承磨损程度，能有效反映轴承摩擦磨损对转子动力响应特性的影响。随着轴承磨损程度的加重，转子的进动幅度逐渐增大，最终可能导致转子发生碰磨导致转子失效。

3.4 转子失效能量计算

根据以上研究结果可知，轴承摩擦磨损会导致转子做二阶进动甚至出现拟周期运动，进一步加剧轴承摩擦磨损和轴所受的交变力。随着轴承磨损程度和交变力的加重，转子的进动幅度逐渐增大，最终可能导致转子失效。本节进一步运用理论方法对比分析转子进动失效与转子无进动失效时释放的最大能量。

1) 无进动失效转子释放的最大能量

假设1台以工作转速运行的柔性支承转子发生破损失效，计算其释放的最大能量。

由于该转子的失效原因为强度破坏，因此转子失效时，其释放的最大能量为以工作转速自转的转动动能，转子的动能计算公式如下：

(13)

式中：Jp为转子极转动惯量；ω为转子工作角速度。计算得到柔性支承转子无进动失效时释放的最大能量为6.001×104J。

2) 进动失效转子的最大能量

假设1台以工作转速运行的柔性支承转子，由于轴承产生摩擦磨损导致转子发生进动，进而导致转子失效，计算此时释放的最大能量。

由于该转子的失效原因为大幅进动，因此转子失效时的运动状态是由多种运动叠加的，其中包括以工作转速自转的运动和以系统二阶进动频率做进动的运动状态，转子失效时，其释放的最大能量为以工作转速自转的转动动能和二阶进动的转动动能，此时，转子的动能计算公式如下：

(14)

式中：J2为转子系统二阶模态的转动惯量；ω2为转子二阶进动角速度。计算得到某型机转子失效时释放的最大能量为6.121×104J，转子释放的最大能量是无进动情况下破损失效模式的1.02倍。

当轴承产生摩擦磨损导致转子发生进动并伴随拟周期运动时，由于进动失效，此时释放的最大能量由工作转速和二阶进动频率、拟周期运动频率线性叠加能量组成。转子的动能计算公式如下：

(15)

式中：J3、J4、J5均为转子做拟周期运动的转动惯量；ω3、ω4、ω5均为转子拟周期运动角速度，ω3=f3×2π，ω4=f4×2π，ω5=f5×2π。计算得到柔性支承转子失效时释放的最大能量为1.380×105J，转子释放的最大能量是无进动情况下破损失效模式的2.3倍。

以上失效能量的理论计算结果说明，在相同转速下，轴承摩擦磨损导致转子发生进动并伴随拟周期运动直至失效时，转子释放的失效能量大幅增加，如果超出装架保护装置的吸能上限，有可能引起同装架机器发生链锁失效的严重后果，因此，在工程中应尽量避免出现轴承摩擦磨损，以防转子出现进动和拟周期运动。

4 结论

本文通过对轴承的运动特性和受力状态进行分析，建立了非刚性连接轴承力学模型，从而建立了轴承非刚性连接的柔性支承转子模型，运用数值方法计算了转子的动力响应，得到如下几点结论。

1) 随着轴承磨损程度的加重，轴承摩擦系数越大，转子的振幅越大，转子的二阶进动也越明显。

2) 随着轴承摩擦磨损加剧，轴承的磨损程度超过磨损等级Ⅳ时，转子产生二阶进动并伴随出现拟周期运动。

3) 轴承摩擦磨损可能导致转子出现不同的失效模式，理论分析结果表明转子二阶进动和拟周期运动会使失效转子释放的最大能量大幅增加。

感谢粒子输运与富集技术国防科技重点实验室姜磊副研究员和杨福江研究员在研究工作中给予的支持与帮助。