公路桥梁正交异性钢桥面板承载疲劳的检测
闫 红
中铁十九局集团第一工程有限公司 辽宁 辽阳 111000
钢桥投入使用后,桥面板受汽车或列车荷载的长期作用,极易发生因疲劳裂纹而导致的事故。仅在1938—1940年间,欧洲就有10座钢桥发生倒塌。1995年,我国广州的海印大桥出现局部斜拉索疲劳断裂的问题,这一类事故均属于由疲劳裂纹引起的突发性倒塌事故[1]。
为提高桥梁的使用寿命和使用安全,众多学者针对钢桥面板承载疲劳检测进行大量研究。
根据文献[2]提出的断裂学理论、文献[3]提出的损伤学理论,相关学者提出了2个不一样的公路桥梁正交异性钢桥面板承载疲劳检测方法,通过计算断裂指数、分析损伤程度,实现对桥梁承载疲劳的检测。
但传统检测方法的定势思维较为严重,所有研究均在公路桥梁正常承载力下完成,难以发现超荷载状态下的桥梁疲劳规律。因此,本文提出公路桥梁正交异性钢桥面板承载疲劳检测研究。
1 公路桥梁正交异性钢桥面板承载疲劳检测方法
1.1 整体钢桥面板组合结构受力行为分析
公路桥梁正交异性钢桥面板承载疲劳检测,首要目标是分析整体钢桥面板组合结构受力行为,即桥梁组合结构的受力情况。正交异性钢桥面板组合结构的受力情况十分复杂,多种桥面荷载向主桁结构传送受力,其中,钢桥面板和桥体小横梁,与下弦杆直接相连,下弦杆除了受主桁变形引起的拉压力以外,还受竖向弯曲作用力的影响。此次检测采用空间有限单元法,分析钢桥面板组合结构受力行为,行为指标包括:桥面荷载传力路径和传力比,该指数关系大横梁和小横梁的受力分析,以及主桁节点荷载和非节点荷载的确认;下弦杆和内系梁的竖向弯曲指数,该指数涉及小横梁间的传力比;桥面荷载对主桁的分配量,该指数关系主桁受力、下弦杆和系梁的竖向弯曲程度[4]。
令大横梁至主桁下弦节点之间的传力路径为L1,另一部分由桥面传至下弦杆,再由下弦杆传至主桁下弦节点的传力路径为L2。其中,路径L1先纵向传力、再横向传力,钢桥面的受力小于总荷载的10%,纵肋受力荷载占比在30%~40%之间,纵梁受力在40%~50%之间。桥面受力后,力经过节点大横梁传递给下弦杆节点,此时该位置的受力小于总荷载的50%;而L2则通过下弦杆将力传给下弦杆节点,此时该位置的受力大于总荷载的50%。设置这2个传力比分别为P1和P2,则P1+P2=1[5]。根据上述传力比,分别计算桥梁中桁和系梁之间、下桁和系梁之间的集中力,公式如下:

式中:F1、F2——中桁和系梁、下桁和系梁之间的集中力;
n——结构之间的受力节间;
φ1、φ2——每一节间内,中桁和下桁分配到的桥面荷 载比;
F*——一个节间桥面荷载总和。
路径L1总的来说没有影响中桁和下桁结构,因此默认P1=F3,即主桁的直接受力值。根据上述受力值,分析钢桥面板的竖向弯曲受力行为[6]。同时,由于公路桥梁的荷载分为一期恒载、二期恒载和活载,因此,以上述系数为参考,计算整体钢桥面板组合结构的受力分配方式。在两主桁结构中,桥梁的荷载是均匀分配的,但在三主桁结构中,该受力分配是不均匀的。由结构力学可知,当3个支座都为刚性时,跨度为2L的梁边支座反力为3qL/8,中支座的反力为10qL/8,二者之比为3∶10,该比例为下桁和中桁的受力之比极限值。通过上述对3个指标的计算,实现对整体钢桥面板组合结构受力行为的分析。
1.2 计算正交异性钢桥面板承载力
面板、纵肋和横隔板组成正交异性钢桥面板,满足桥梁的不同受力需求,因此,在上述整体受力行为分析的基础上,计算正交异性钢桥面板承载力。图1为正交异性钢桥面板受力传力过程[7]。
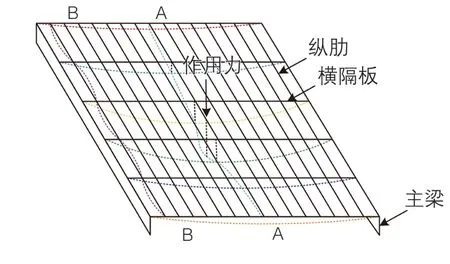
图1 正交异性钢桥面板受力传力过程
根据图1可知,桥面板作为纵肋和横隔板上的一部分,直接承受荷载,又与主梁共同支撑桥面。在荷载作用下,正交异性钢桥面板承受桥面荷载,先将荷载传递给纵肋,然后传递给横隔板,最后传递给主梁。因此,根据上一节的分析结果,将正交异性钢桥面板分为主梁体系、桥面结构体系和面板体系。
主梁体系的力学分析与一般梁相似,因此,可以按照初等梁弯曲计算方法确定具体取值,这里就不再过多描述。而桥面结构体系,沿纵桥向方向,简支在钢箱梁的腹板上,沿横桥向方向,弹性支撑在横隔板上。
从以往的研究结果可知,该结构体系的实际承载能力大于小挠度弹性计算求得的支撑力,因此按照正交异性钢桥面板理论计算其承载力,采用的计算方法为P-E法。该方法做出如下3个假设:正交异性钢桥面板简支在顺桥向的钢箱梁腹板上,弹性支撑在横桥向的等间距横隔板上;钢箱梁的腹板抗弯刚度为无穷大;横向抗弯刚度等于桥面板刚度。
该方法在第一阶段计算纵、横隔板的弯矩最大值,并求出横隔板位置的支反力;然后在第二阶段考虑横隔板的柔度,修正第一阶段的计算结果。
面板体系直接承受荷载的局部作用,并将荷载传递给纵肋、横隔板。而桥面板受力呈膜应力状态,具有极大的超载能力,是造成面板疲劳开裂的重要因素,因此,本次研究考虑面板体系的膜应力状态,对公路桥梁正交异性钢桥面板承载疲劳进行检测时,必须考虑第三体系的承载力。采用弹性薄板理论分析面板体系,将面板看成支撑于弹性肋上的各向同性板,如图2所示[8]。
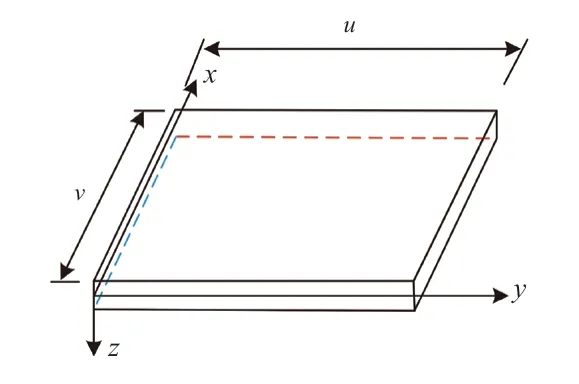
图2 正交异性钢桥面板三维坐标系
然后进行承载力计算,同时默认纵、横隔板的刚度均匀分布,且与面板共同受力,则面板横、纵向抗弯刚度分别为:

式中:Wx、Wy——横向、纵向抗弯刚度;
E——弹性模量;
Ix、Iy——横向、纵向截面惯性矩;
u、v ——横、纵隔板间距。
按桥面体系计算时,参考下列平衡微分方程:
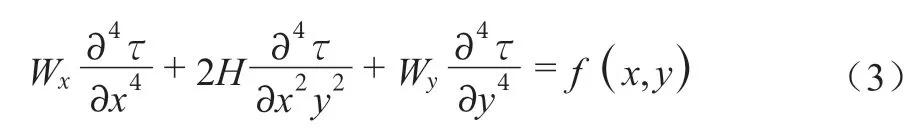
式中:τ ——正交异性板上的中间点在竖直方向上的挠度;
f(x , y)——z方向的分布荷载;
H——抗扭刚度。
按照薄板理论求得上述公式后,求解式(3),得到齐次方程的一般解τ1和τ2,即τ1+τ2=τ。将结果代入式(2),得出实际抗弯刚度,至此完成对正交异性钢桥面板承载力的计算。
1.3 检测正交异性钢桥面板的疲劳程度
根据上述计算结果,以传统正交异性钢桥面板有限元模型为参考,建立新型桥面板有限元模型,通过设定疲劳评价指标,检测正交异性钢桥面板的疲劳程度。由于该模型的建立与传统模型的构建方法较为相似,因此,不再着重描写该模型的建立过程。
对钢桥面板进行承载疲劳检测时,利用名义应力法和热点应力法,设定疲劳评价指标。名义应力的取值,通常以裂纹附近处的应力值为标准,根据弹性理论获得,即利用S-N曲线,得到结构名义应力,以此来评价桥面板的疲劳程度。
对于比较复杂的结构连接部位,一次名义应力的计算是存在误差的,需要进行多次计算,取其平均参数作为标准名义应力,这是对于单一连接结构来说的。而对于由多个零件组成的复杂结构来说,需要利用热点应力法来评价桥面板的疲劳程度。热点应力法,首先要确定热点应力类型,而该类型按照结构衔接位置,可分为3种结构,如图3所示[9]。
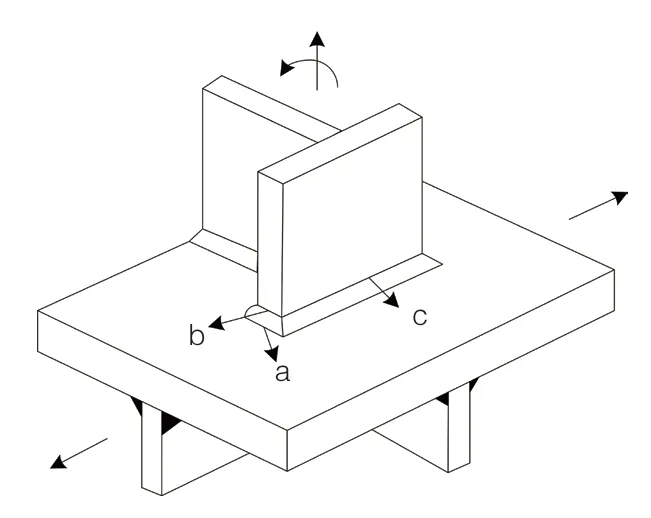
图3 3种热点应力相对位置
根据图3可知,类型a位于附板的根部或者母板的表面,类型b位于附板的端面边缘,类型c沿母板的衔接方向分布,则利用热点应为外推法,对2个衔接点或3个衔接点的结构进行线性差值计算,公式为:式中:δ1——两点线性外推计算结果。
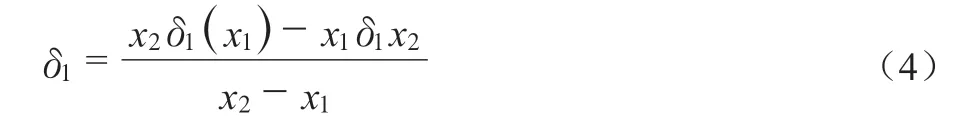
根据设定的评价指标,检测正交异性钢桥面板的疲劳程度,计算公式为:

式中:μ ——膜应力;
Wx,y——式(2)所得抗弯刚度;
t ——板厚度;
gt——板厚方向的应力分布。
由于桥梁面板多为复杂结构连接,因此检测复杂钢桥面板的承载疲劳程度时,不再使用名义应力[10]。根据以上内容检测正交异性钢桥面板的疲劳程度,实现对公路桥梁使用性能的分析。
2 试验研究
将此次提出的检测方法作为试验组,将依据文献[2]、文献[3]提出的传统检测方法,分别作为对照1组和对照2组,进行仿真对比试验,检验不同检测方法,是否可以在同样的试验环境下使用。
2.1 试验准备
利用仿真试验环境模拟一个由正交异性钢桥面板建立的公路桥梁。为保证试验数据与实际工作相符,根据钢桥面板各个主要构造细节的标准疲劳强度允许值,构造模拟桥梁。
令试验测试所用的桥梁模型与真实桥梁属性和参数保持一致。设置2个试验环境,第1组试验环境:没有大型货车通行,无超载车辆,日均车流量较小;第2组试验环境:有大型满载车辆通行,来往的大、中、小型货车中,45%的货车为一般超载,15%的货车为严重超载,且日均车流量大。测试2个试验环境下,公路桥梁模型的工作状态。运行无异常后,以上述试验环境为变量,利用3个测试组,检测不同试验环境中正交异性钢桥面板的承载疲劳程度。
2.2 第1组试验测试与分析
使用第1组测试环境,已知该环境中与4个结构相连接的钢面板承受的荷载较小。图4为3个检测方法的承载疲劳检测结果。
试验测试通过失效系数来评价疲劳程度。图中4条曲线为与钢桥面板相连接的4个部位的桥面失效曲线。根据图4可知,3个测试组得到的失效系数具有相似的变化规律,可见第1组桥梁疲劳检测结果可信。导出具体数据后可知,3组方法的疲劳计算结果非常相似,可见3种方法在第1组试验环境中具有很好的性能。
2.3 第2组试验测试与分析
重置试验环境和测试软件,对第2组试验环境下的桥面疲劳程度进行检测。已知该环境中与4个零件相连接的钢面板承受的荷载较大。图5为第2组试验测试对比结果。
根据图5所示结果可知,试验组失效曲线同样具有一定的变化规律,而对照1组只有曲线A与试验组相似,对照2组只有曲线C和试验组相似,2个测试组中的其他失效曲线波动剧烈,完全失去规律性。
经逐步排查,证实试验硬件与测试软件均不存在故障,人为操作也没有出现失误的现象,可见2个传统的疲劳检测方法无法适用于第2组测试环境,同样也无法应用到实际工作中。
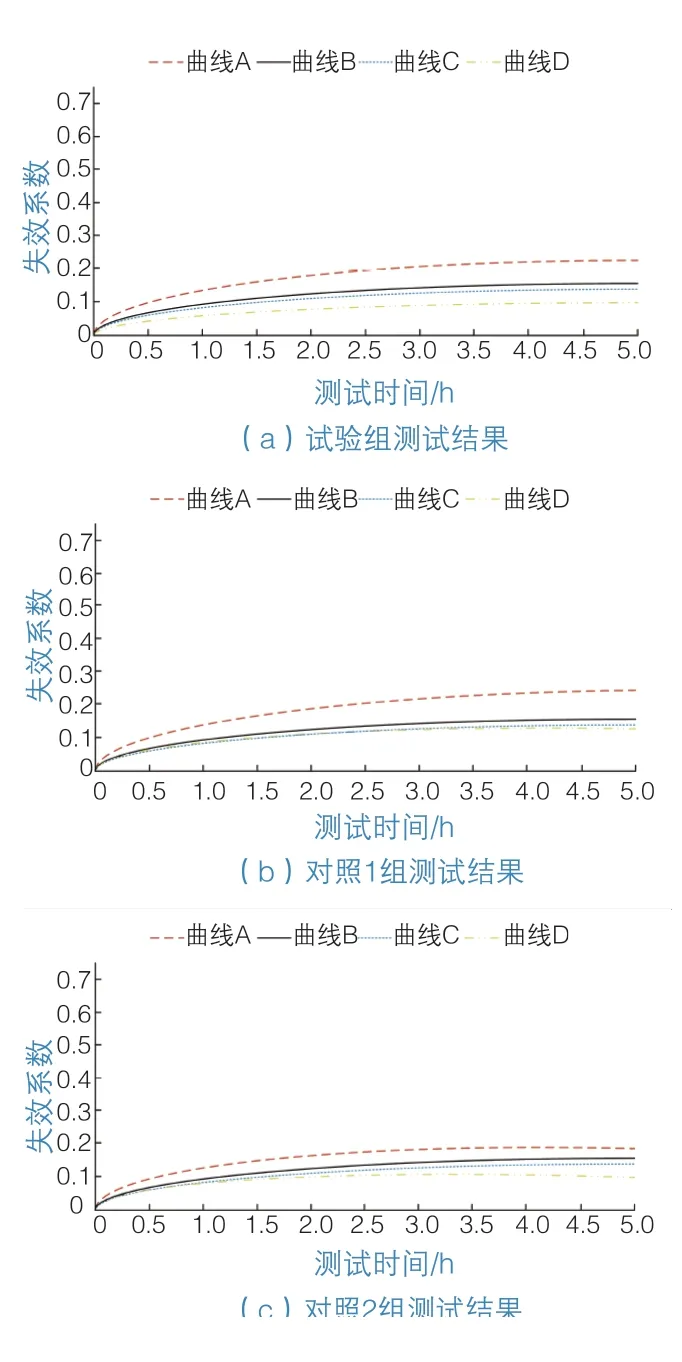
图4 疲劳程度检测结果
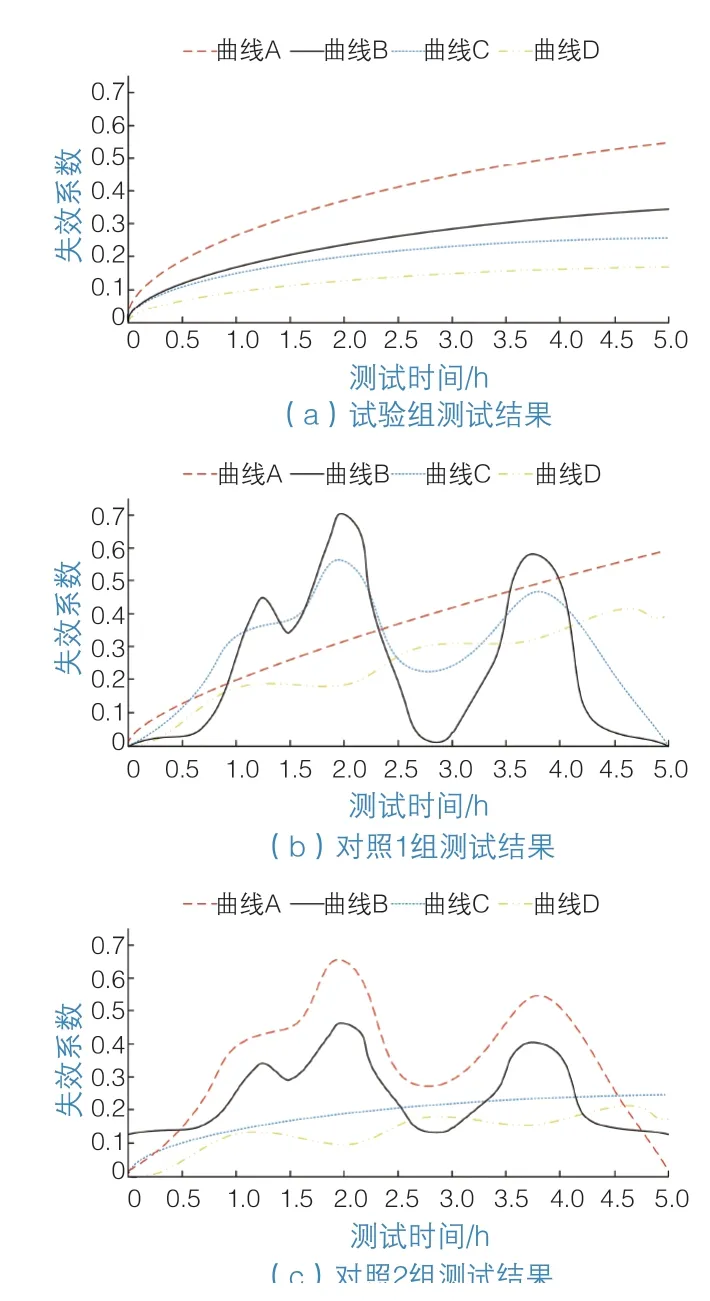
图5 疲劳程度检测结果
鉴于第2组测试结果中对照组的试验结果脱离实际,因此不再计算疲劳值。
3 结语
此次研究的钢桥面板承载疲劳检测方法,从3个结构体系上计算桥面板的承载能力,没有忽视任何一个细节,从而令检测方法适用于日均车流量大、来往车辆超载率高的公路桥梁,使检测结果贴合公路桥梁的实际使用状态。但此次没有详细介绍桥面板有限元模型的建立过程,因此今后可以对该模型的建立进行分析说明,重点介绍建模使用的各项参数[11]。

