基于FLUENT的垂向二维数值波浪水槽的造波效果*

童朝锋，魏芷阳，孟艳秋

(河海大学 港口海岸与近海工程学院，江苏 南京 210098)

基于FLUENT流体力学模型建立数值波浪水槽是波浪与建筑物之间相互作用研究的经典方法，周勤俊等[1]基于RANS方程和两方程湍流模型，采用有限体积法，首次提出了适用于VOF方法的源造波、消波技术;其后孙大鹏等[2]、赵艳等[3]采用计算流体力学模型成功利用源项、推板、速度边界造波法建立基于FLUENT的数值波浪水槽，FLUENT流体力学模型开始广泛应用。近年来国内外新的数值造波方法层出不穷，Jacobsen等[4]将基于BOUSSINESQ水波方程的造波方法成功应用到了开源代码OpenFOAM中取得了较好的造波效果;Wang等[5]基于CIP模型成功模拟了孤立波与水下建筑物的相互作用；Losada 等[6]、Higuera等[7]分别建立了基于COBRAS-UC模型、OpenFOAM模型的数值波浪水槽模型模拟了波浪与建筑物之间相互作用过程，取得了较好的效果。

相比之下，FLUENT作为最常用的计算流体力学模型，操作简便、界面友好，具有先进的数值仿真和强大的前、后处理功能，在计算流体力学领域和实际工程中具有极强的应用价值。基于FLUENT的数值造波方法根据造波原理主要有源项造波法、推板造波法和速度边界造波法3种。为达到波浪的精准数值仿真，须充分了解各种造波法造波效果以及达到最佳造波效果应采用的网格尺寸，但目前尚无相关文献对此进行详细对比分析。

为此，本文应用FLUENT流体力学计算模型，采用上述3种造波法，分别建立不同网格尺寸和波陡条件下的数值波浪水槽，结合线性波和二阶、三阶Stokes波理论，对比不同方法的仿真结果及与理论波浪形态之差异，分析3种造波法的优缺点，讨论采用不同波浪方程、不同网格尺寸对仿真结果的影响，为利用数值波浪水槽开展波浪与建筑物相互作用数值研究提供根据。

1 造波、消波原理及边界条件设置

1.1 数值波浪仿真模型

波浪数值仿真采用FLUENT流体力学软件，其软件选取显式或隐式差分格式，非耦合隐式算法、耦合显式算法或耦合隐式算法等数值计算方法求解Navier-Stokes方程，可精确模拟层流、湍流、多相流等各类流体力学问题，软件提供用户自定义函数便于二次开发。本文数值波浪水槽模拟采用二阶迎风格式、PISO算法、k-ε模型，结合VOF模型和几何重构法进行液面捕捉，获得较为精准的模拟结果。

1.2 造波原理及边界条件

1.2.1源项造波法

源项造波法原理是通过UDF二次编译功能在造波源区域给动量方程添加动量源项s(x,y,t)，使造波源区域中水质点具有运动速度，并在重力作用下水面升降形成波浪。根据相关文献[8-9]，造波源区域高度宜取水深的23，或使造波源区域上方水体高度约为1倍波高，宽度宜取波长的150。实际计算时可选取大致合适的尺寸，再不断试算调整选取最佳造波源尺寸。

数值水浪水槽如图1所示。造波源区域设在入口处，波浪沿x方向传播，右端为消波区，消波区长度取1～2倍波长。水槽入口、出口及下部边界均取固壁边界，上部为压力出口。

图1 数值波浪水槽

造波源函数根据以下公式确定：

(1)

(2)

式中：s(x,y,t)为造波源区域要添加的造波源项；u(x,y,t)为t时刻目标波浪在坐标(x,y)处的水质点水平速度，根据线性波理论或Stokes波理论取值；u、v分别为x、y方向速度；Δx为水平方向网格长度。

1.2.2推板造波法

推板造波法原理与物理模型中推板式造波机相同，其数值波浪水槽与图1相同，入口处固壁边界添加动网格以模拟推波板运动。

推板运动速度根据Schaffer等[10-11]推得的推板位移变化与波面高度之间解析关系确定，其水平运动速度函数u(t)如下：

(3)

(4)

式中：η为波面升高，根据Stokes波理论或线性波理论确定其值；ω为角频率；c0为造波板运动与给定波浪间的传递函数；k为波数；d为水深。

1.2.3速度边界造波法

速度边界造波法将入口边界水质点赋予已知相应波水平和垂向周期性振荡速度，促使水质点运动产生波浪，其数值水槽与图1相同。数值水槽的造波区入口处边界设为速度入口边界，水槽底部和右侧为固壁边界，上部为压力出口边界。

数值水槽入口边界处水质点水平向和垂向速度：

u=u(x,y,t)

(5)

v=v(x,y,t)

(6)

式中：u，v分别为入口边界水平、竖直方向速度；u(x,y,t)、v(x,y,t)分别为在t时刻坐标(x,y)处水平、竖向速度，其值根据线性波理论或Stokes波理论确定。

1.3 消波方法

采用动量源消波。在消波区，水体动量方程添加阻尼源项：

(7)

(8)

式中：ρ为水密度；p为水压力；μ为消波系数，为使波浪平缓过渡，μ随x由0递增，即:

μ=a(x-x0)

(9)

式中：a为常数，根据经验其取值范围为1～50；x0为消波区起始位置水平坐标。

2 模型建立

2.1 网格及模拟工况

波浪要素见表1，波况1～3保持水深和波高不变，只改变周期达到改变波陡的目的。波况1～3采用的水槽总长280 m、高10 m、水深6 m，消波区长30 m。为方便比较，考虑尽可能少的影响条件，波况4采用总长140 m、高8 m、水深6 m的深水数值水槽，探究非线性项对造波效果的影响，水槽消波区长20 m。

表1 数值水槽波况参数

采用a、b、 c、d、e共5种结构化网格，其中网格a水平分辨率Δx=0.4 m，垂向分辨率Δy=0.02 m；网格b的Δx=0.4 m，Δy从液面附近向两边递增，最小为0.02 m，最大为0.1 m；网格c的Δx=0.4 m、Δy=0.05 m；网格d的Δx=0.4 m、Δy=0.12 m；网格e的Δx=0.1 m，Δy从液面附近向两边递增，最小为0.004 m，最大为0.06 m。

为探究垂向网格分辨率对模拟结果的影响，波况1采用a、b、c、d4种网格分别建立数值波浪水槽。网格e用于波况4深水情况下微幅波的模拟计算。波况1～3分别采用3种造波法和线性波、二阶Stokes波两种波浪方程进行模拟，以探究造波法对造波效果的影响。波况4采用3种造波法和线性波、二阶、三阶Stokes波方程进行模拟，研究数值造波中非线性作用的影响。算例模拟时间步长取0.01 s，每步最多迭代40次，计算总时间超过80 s。

2.2 造波和消波验证

使用波况1(波陡Hλ=0.043)、网格b、二阶波浪方程，则3种造波方法得出的x=λ处水面变化历时曲线如图2所示。3种模拟结果都在时间t=10 s左右达到稳定，之后水面随时间规律性变化，且与理论值吻合良好。模拟得出的x=λ处一个周期内速度和动压强与理论值对比见图3。取波峰处时间为T4,波谷处时间为3T4，可以看出模拟值与理论值基本吻合，说明基于FLUENT建立的数值波浪水槽可用于波浪与结构物之间相互作用的研究。

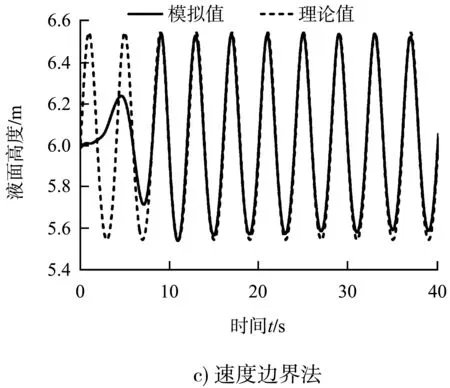
图2 3种造波法x=λ处液面历时曲线

波况1使用推板造波法、二阶波浪方程,t=60 s时水槽末端水质点速度矢量分布见图4。结果显示在非消波区水质点运动速度较大，消波区水质点运动速度逐渐减小，最后变为0，说明消波区消波效果良好。

图3 推板造波法x=λ处水质点速度、动压强与理论值对比

图4 t=60 s时水质点速度矢量分布

3 结果对比与分析

3.1 网格分辨率对数值造波效果影响

采用上述3种造波法、二阶波浪方程和4种不同垂向分辨率的网格分别建立数值波浪水槽，模拟仿真波况1的波浪。为便于辨析某一位置处模拟波面与理论波面贴合程度，将自由水面和波高的理论值均取该点处模拟波的平均水面和波高，采用如下均方根相对误差计算一个周期内模拟值与理论值相对差异，评价模拟仿真效果：

(10)

式中：S为均方根相对误差；H为波高；ηi为i时刻理论液面高度；η′i为i时刻模拟液面高度；n为一个周期内的数据数量。

不同造波法所造波浪平均水面飘移随网格分辨率变化如图5a)所示。源项造波法模拟仿真的水面漂移绝对值受网格尺寸变化影响较大，液面附近垂向网格分辨率Δy取0.02 m时波面漂移绝对值为0 m，随Δy增加，迅速增加到0.07 m左右；推板造波法模拟结果在Δy≤0.05 m时水面漂移绝对值集中在0.015 m附近，当Δy=0.12 m时偏移量急剧增加至0.06 m；速度边界造波法模拟仿真结果随网格步长增加波面漂移量变化不明显，基本保持在0.02 m左右。

液面高度相对差异随网格分辨率变化如图5b)所示。采用源项造波法得出的模拟波形与理论波形之间误差最大，随网格变化误差增加最快；采用推板造波法得出的模拟波形与理论波形吻合最好，相对误差均较小；使用速度边界法模拟值在Δy≤0.05 m时误差较小，Δy=0.12 m时误差急剧增加。

注：波况1，Hλ=0.043,x=λ处；Δy为0.02、0.02～0.10、0.05、0.12 m分别对应网格a、b、c、d。

图5采用不同造波方法的水面漂移绝对值和仿真与理论液面高度相对差异随不同网格分辨率变化

波高沿程变化如图6所示。可以看出，采用不同分辨率的网格建立数值波浪水槽，随波浪传播距离增加，采用不同网格模拟得出的波高值产生差异。其中使用源项造波法造波得出的波高差异最大，使用推板造波法得出的波高差异最小，采用速度边界造波法得出的沿程波高在网格垂向分辨率Δy≤0.05 m时基本相等，使用Δy=0.12 m的网格时得出的沿程波高与使用其他网格得出的模拟值差异较大。波高随传播距离增加持续衰减，衰减到一定程度后逐渐稳定，这是由数值耗散和水体黏性影响产生的正常现象，实际应用中可以增加起始波高，在波高趋于稳定的位置放置建筑物。

图6 波况1使用不同造波法沿程波高对比

综上，垂向网格步长越小模拟结果越精确，源项造波法模拟仿真波浪效果对垂向网格分辨率变化比较敏感，液面附近垂向网格分辨率取Δy=0.02 m，即Δy=H50(H为波高)时即可取得较为精确的结果；推板造波法和速度边界造波法模拟结果对网格分辨率变化敏感性相对较弱，垂向网格分辨率Δy=0.05 m，即Δy=H20时模拟效果较好。

3.2 波陡对数值造波效果影响

根据上述网格对3种造波法造波效果影响分析结果，采用网格b对波况1～3模拟计算，讨论波陡对数值造波效果影响。计算分别采用了3种造波法和2种波浪方程。

模拟结果在x=25 m处水面漂移绝对值见图7。可以看出，波陡相同时采用速度边界法得出的水面漂移绝对值最大，源项法最小；就波浪方程而言，其他条件相同时，采用不同波浪方程得出的水面漂移绝对值基本相等，说明采用的波浪方程不是影响水面漂移的主要因素。

图7 不同波陡条件下采用不同波浪方程模拟x=25 m处水面漂移绝对值

模拟结果在x=25 m处一个周期内液面高度与理论值的相对误差S见图8。可以看出，其他条件相同时，采用不同波浪方程仿真得出的结果与二阶Stokes波理论值吻合均较好。说明造波源不管采用哪种波浪方程，在波浪传播过程中，模拟结果都会受边界的非线性作用影响，使波浪呈现出非线性波特性。

图8 不同波陡和波浪方程模拟液面与理论液面误差

仿真得出的沿程平均波高对比见图9。可以看出，采用速度边界造波法得出的沿程平均波高最大，采用源项法最小；其他条件相同，波陡增大波高衰减速度变快；只改变波浪方程对比模拟结果，使用二阶波浪方程得出的沿程平均波高普遍高于使用一阶方程得出的结果，波陡越大两者差异越不明显。

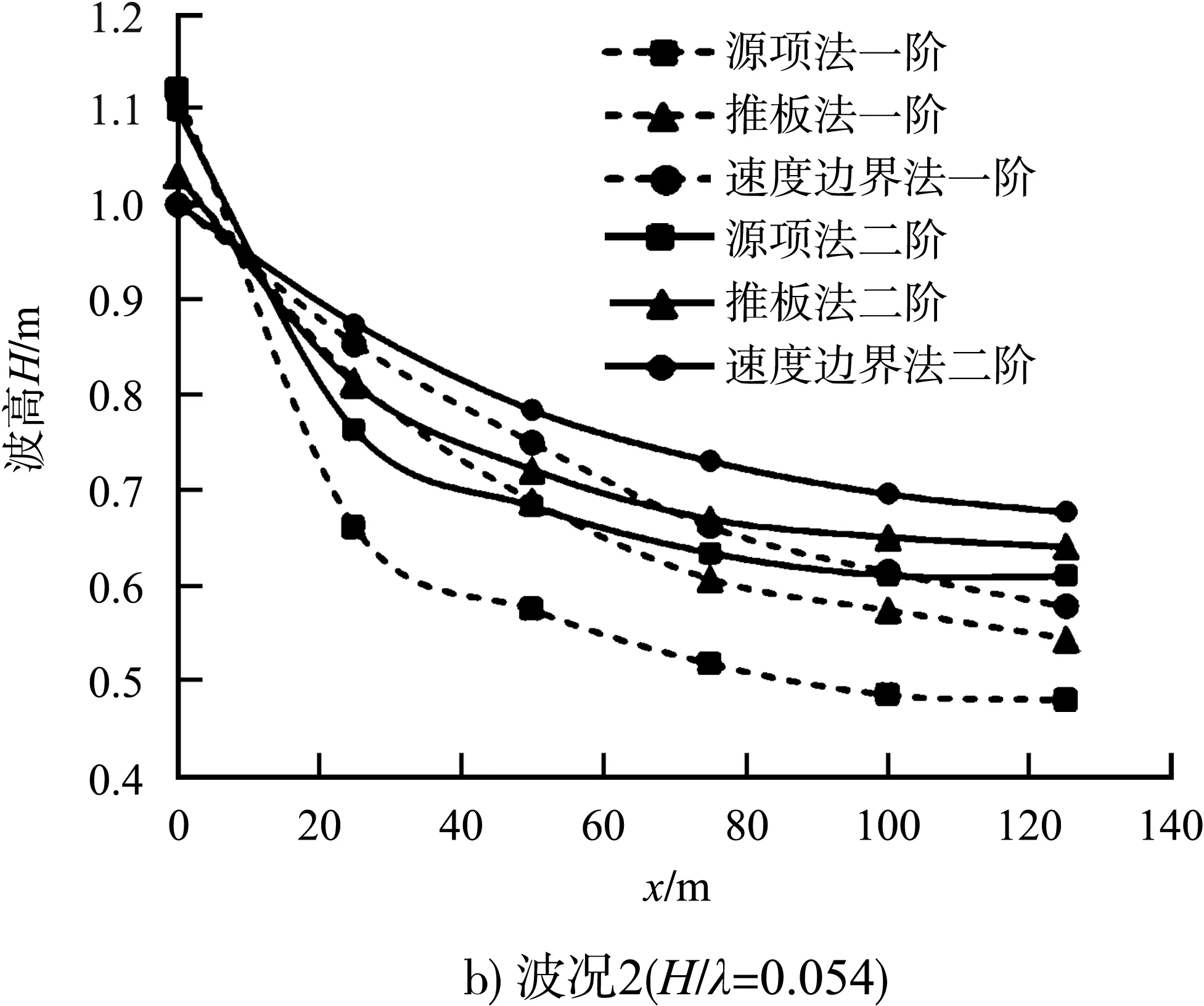
图9 采用不同造波法和波浪方程模拟沿程平均波高对比

3.3 数值造波中的非线性作用影响

根据上述波陡对数值造波效果影响结果，无论使用哪种波浪方程建立数值波浪水槽，在波浪传播过程中都会使模拟波面变化接近二阶Stokes波理论值。增加波况4(Hλ=0.021)，深水数值水槽算例，研究采用不同波浪方程对造波效果影响。计算分别采用一阶、二阶、三阶波浪方程,其水面漂移绝对值见表2。可以看出，造波方法相同时，使用不同波浪方程得出的水面漂移绝对值完全相等。模拟波面与理论波面相对误差如图10所示，造波方法相同时采用的波浪方程阶数越高模拟值与同阶理论值之间相对误差越小；低阶波传播过程中受非线性影响，模拟值与相应理论值相对误差反而大。高阶波波形已经体现了非线性项的变形作用，传播过程中反而变形较小，其模拟值与理论值之间误差也较小。

表2 波况4在深水情况下水面漂移绝对值

图10 波况4在深水条件下模拟波面与理论波面相对误差

4 结论

1)采用源项造波法造波，波高沿水槽衰减最快；推板造波法采用动网格技术，计算效率相对低，数值造波波形与理论波形最接近；采用速度边界造波法计算效率最高，数值波高沿水槽衰减速度最小。

2)网格越细模拟结果越精确，采用源项造波法模拟结果对网格尺寸变化最敏感，采用推板造波法和速度边界造波法模拟结果对网格尺寸变化较不敏感。

3)数值水槽计算中，波陡越大波高衰减越快；数值波浪模拟显示，在数值水槽的波浪传播有非线性作用影响，导致即使造波是线性波，传播到一定距离后，波面也有非线性变形。