基于物理模型的“同心协力”策略探究

韩子星 鹿栖苑 王洋洋

（华北理工大学数学建模创新实验室 河北 唐山 063210）

引言

假设鼓的形状为圆柱体，绳子固定点的位置位于鼓侧边的中心；假设装置固定良好，不易散架，鼓的材质均匀一致；假设所有人拉绳子的力相同且均为恒力；忽略鼓与水平面夹角对拉力在竖直方向上的分量的影响。

1 模型准备

转动是机械运动的一种基本形式，它是指运动物体上，除转动轴上各点外，其他各点都绕同一转动轴线作大小不同的圆周运动[1]。

在题目中给出的数据中,可以大致确定它们的转轴，并将它们进行分类[2]。

（1）第一类：第1、4、7组，只有第一个人的发力时机或用力大小与其他人不同，所以转轴为过鼓的中心且平行于第3、7号队员连线，如图1(a）所示。

（2）第二类：第2、5组，只有第1、2个人与其他人的行为不同，但1，2号队员之间相同,因此转轴平行于3、4号选手的角平分线，如图1(b)所示。

（3）第三类：第3、6、9组，只有1、4两人相同且与其他人不同，则转轴平行于4、5号队员的角平分线，如图1(c)所示。

（4）第四类：第8组，对称性弱，不易看出。

基于以上分类，进行求解，所求倾角如表1所列。

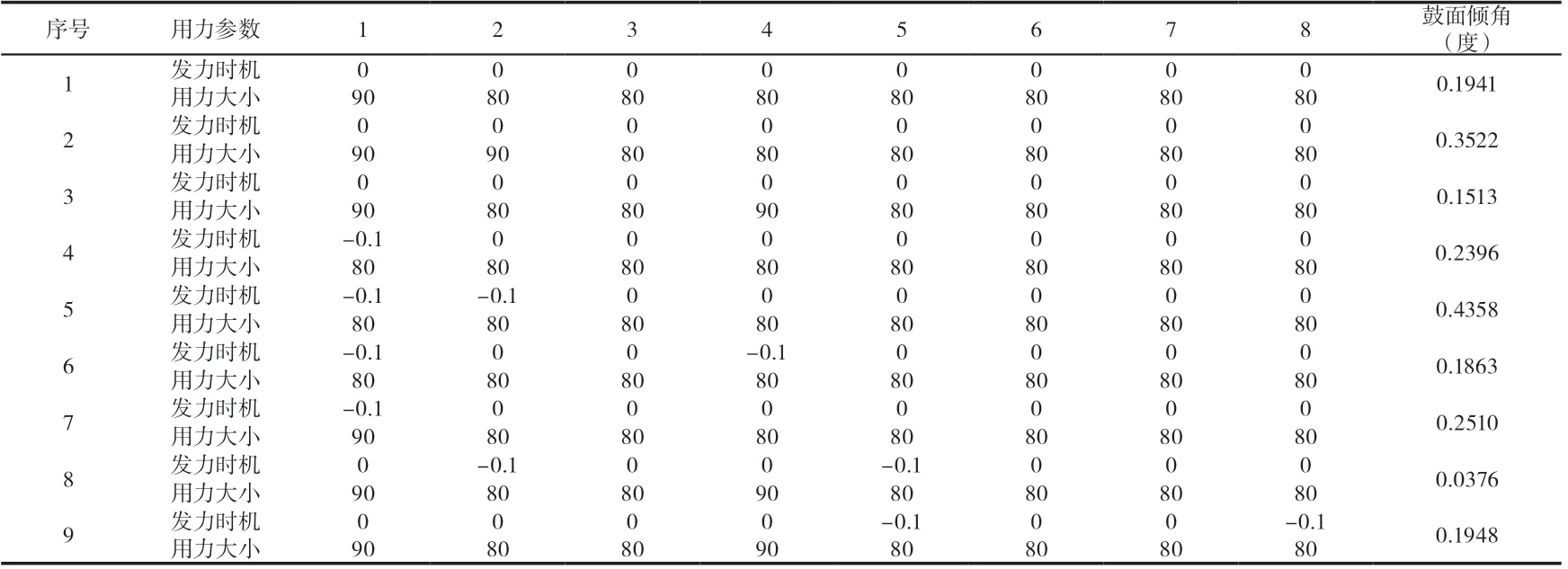
表1 鼓面倾角

2 策略调整

如图4所示，设球沿着第1、2位队员之间1:2的方向所在竖直面内移动，为了把球调整成竖直,需要在下次接到球时鼓面往反方向倾斜0.5°，即要鼓绕着图中的轴线旋转使得第1、2位队员之间1:2的方向上升0.5°。这需要使合力矩始终沿着转轴的方向[3]。

要使得鼓始终绕着轴旋转，合力矩必须始终垂直于轴，即沿轴方向的分量零。为了使此分量恒为零，需要h和α的系数均为零[4]。

求得一组满足上述条件的解如下，

假设鼓面初始时刻是水平的，初始位置较绳子水平时下降0.15m，将以上数据代入平动公式中，即

得到倾角公式为

根据（3）式可得如下图像，

由图可知，速度v1在前0.1s时随时间增大而增大。当t=0.0423s时的速度恰好能使球上升至0.4m处。当t=0.062时，v1较前者更大，故满足使球上升至少40cm的要求，则该策略合理[5]。

3 结束语

本文就同心协力鼓在转动情况下的“同心协力”策略的研究，基于四类不同发力情况，建立三维物理模型，根据2019年全国大学生数学建模竞赛B题的数据，计算得出了不同情况下的鼓面倾角。后续又进行了策略的调整，使其能满足球上升至少40cm的要求。本文所建立的三维物理模型，利用数学物理方法，较为准确地分析了“同心鼓”游戏在理想条件以及鼓转动条件下的物理过程，能为游戏参与者提供指导性意见，帮助参与者取得更好成绩。