数形结合巧运用 思维能力妙培养

张玉翠

（福建省厦门市同安区第二实验小学，福建厦门 361100）

引 言

著名数学家华罗庚指出：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休。”数形结合是学生解决数学问题时常用的一种思想方法[1]。无论是“以形助数”，还是“以数赋形”，都能使抽象的数学问题变得直观、形象。由此可见，在数学教学中运用数形结合的思想，有助于培养学生的思维能力，提升学生的数学素养。下面笔者结合自身的教学经验，谈谈如何借助数形结合思想来培养学生的思维能力。

一、运用数形结合，培养形象思维能力

形象思维能力是指依托具体的图像或形象，帮助学生理解数学知识，从而解决问题的一种思维能力。在计算教学中，有些算理很抽象，教师不妨把计算教学与直观图像结合起来，使之形象化，以此培养学生的逻辑思维能力[2]。

（1）在练习本上画一个比较大的正方形，当作单位“1”；

（2）在正方形这个单位“1”里画出计算题中的每个分数，并标上分数值；

（3）观察所画的图，思考：你发现了什么？

在展示交流时，学生画的图如图1所示。

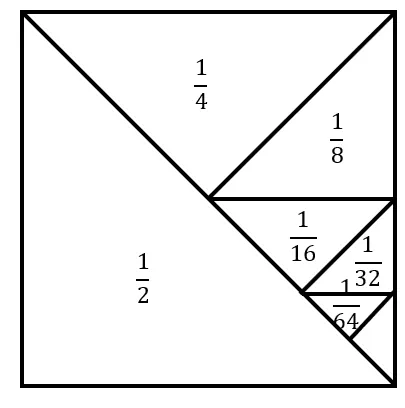
图1

教师借助图形这一工具，使数与形巧妙结合，把数学问题从图形上视觉化，利用图形的直观性引发学生思考，从而引导学生发现解题思路。数形结合能够充分调动学生的形象思维，使形巧妙地反映数的内在联系，直接揭示问题的本质，把复杂问题简单化，同时渗透极限思想，使学生做到心中有图见数、有数见图，思维也得以拓展。

二、运用数形结合，培养逻辑思维能力

逻辑思维能力是指正确合理思考问题的能力，是学好数学必须具备的能力。教师运用数形结合思想，将复杂的数量关系与直观的几何图形联系起来，能使抽象问题具体化，有助于培养学生的逻辑思维。

图2

此时教师做如下引导：观察线段图，你能发现什么数量关系？学生观察图充分理解后，汇报整理如下：

（1）菊花2 份，月季花3 份，共5 份是60 盆；

（4）菊花与月季花的比是2∶3，菊花与总数的比是2∶5，月季花与菊花的比是3 ∶2，月季花与总数的比是3 ∶5；

厘清数量关系后，学生的解题思路自然打开，得出了以下几种解法。

第一种解法：根据总数与部分数之间的关系。

第四种解法：利用比的知识进行解题。

菊花：60÷（2+3）×2=24（盆）月季花：60÷（2+3）×3=36（盆）

教师借助线段图，“以形助数”使数量关系更加明显、直观，使学生的解题思路更加开阔，呈现出多样化的解题方法。学生在画线段图的过程中经历了由“文字表征”向“形象表征”再到“数学表征”的转换过程，这一过程给学生提供了广阔的思维空间，需要学生主动地进行观察、分析等一系列智力活动才能实现，有效培养了学生的逻辑思维能力，提高了学生的学习能力。

三、运用数形结合，培养空间想象能力

教学实践表明，空间想象能力较弱是学生学习几何知识遇到的最大难题。学生在面对文字描述时无法在大脑中呈现出相应的图像，数形结合的方法可以很巧妙地打破这一困境。

例如，一个平行四边形，如果底增加2 厘米后，面积增加20 平方厘米；如果这条边上的高增加4 厘米，面积增加60平方厘米。原来平行四边形的面积是多少平方厘米？这道题综合性强，复杂且抽象。乍一看，学生会感觉很难，不知如何解答。教师可引导学生根据题意来画图（如图3）。

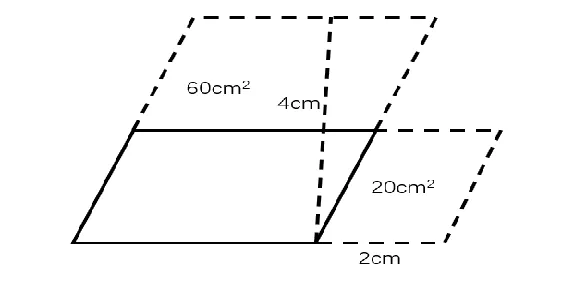
图3

通过画图，教师引导学生观察，从而得到：根据“底增加2 厘米，面积增加20 平方厘米”，可以求出原来平行四边形的高，即20÷2=10（厘米）；同样的根据“高增加4 厘米，面积增加60 平方厘米”，也可以求出原来平行四边形的底，即60÷4=15（厘米）；然后可以求出原来的平行四边形的面积：10×15=150（平方厘米）。

此题借助几何示意图，使复杂问题简单化，无形地使解题思路形象化，激活了学生的形象思维，使学生的空间观念在解题的过程中逐步养成，从无到有，从模糊到清晰。数形结合帮助学生建立了几何表象，有效弥补了学生空间思维上的不足，提高了学生的空间想象能力。

四、运用数形结合，培养创造思维能力

创造性思维是指学生在解决问题的过程中，能分析题意，发现问题，找到独特的解决问题的方法或提出富有创造性的设想。教师要巧妙运用数形结合，激发学生的创新意识，培养学生的创造性思维。

例如，在学完梯形的面积后，教师出示了练习题（见图4），让学生计算图中圆木的总数。大部分学生列式：3+4+5+6+7+8+9+10=52（根）。其中一名学生提出了自己的看法：如果再多几层，还用这种方法计算太麻烦了；另一名学生提出了自己的猜想：这个图形看起来像梯形，是否和梯形的知识有关？学生创新的火花在闪耀。此时教师出示图5。

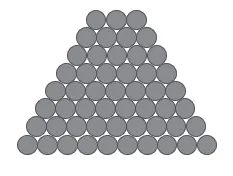
图4

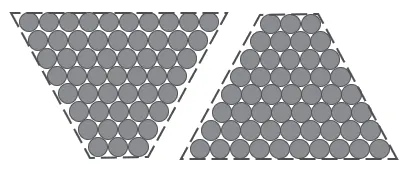
图5

教师带领学生观察图形，分析得出：两个完全一样的梯形拼成了一个平行四边形，平行四边形的底边根数由两部分组成，即梯形圆木的顶层根数和底层根数之和。这些平行四边形圆木，每层有(3+10)根，有8 层，一共有(3+10)×8=104（根）；梯形圆木的根数是平行四边形圆木根数的一半，所以这堆梯形圆木的根数是：(3+10)×8÷2=52（根）。再与原来的图形进行类比，学生发现这和梯形的面积公式（上底+下底）×高÷2 类似。这样通过类比图形，学生深刻地理解了这道题的难点，创造性地解决了问题。

接着，教师出示这样一道计算题：3+4+5+6+…+100=？有了前面的学习经验，学生脑海里马上会闪现出相应的图形，并列出算式：(3+100)×98÷2=5047，进而总结出解决这一类问题的模型：（顶层根数+底层根数）×层数÷2。

在数与形的相辅相助中，学生另辟蹊径地解决了原本烦琐的问题，成功突破了习惯性思维定式的约束，展开了巧思妙想。数形结合的巧妙运用，有效培养了学生的探索精神，提高了学生的创造性思维能力。

结 语

总之，在实际教学中，教师应善于挖掘教材内容，积极合理地把“隐性”的数形结合思想方法“显性”地传递给学生，将复杂的数学知识简单化，从而提高学生的学习效率，使学生在潜移默化中日积月累，达到培养学生思维能力的目的。