残骸落区对火箭构型影响论证
周天帅,张博俊,周 桃
(北京宇航系统工程研究所,北京 100076)
0 引言
近年来,随着科技的不断进步,现有运载火箭已经逐渐不能满足发射任务的需求。更大的载荷、更先进的发动机、更经济的发射费用是未来新运载火箭的设计目标。随着我国经济的高速发展,地方建设水平的日益提高,已经很难再划出新残骸落区,仅能继续使用现役运载火箭已有落区[1]。运载火箭的残骸落区与上升段弹道密切相关,对残骸落区的约束将直接反映在上升段的设计上,进而影响火箭的运载能力。
另一方面,若上升段轨道偏离最优运载能力轨迹,则往往带来燃料加注规模的浪费,在这种情况下,需要调整运载火箭各级的加注规模,即对火箭构型的整体方案进行微调。
由此可见,残骸落区的选择直接关系到运载火箭构型方案的选定。因此,有必要分析约束残骸落区对运载火箭上升段轨道设计及构型的影响,为未来构型论证工作的开展夯实基础。
运载火箭上升段轨道设计是多约束、多控制变量优化的构型设计问题,过程复杂、工作量大。杨希祥等[2]探讨了应用粒子群优化算法的运载火箭上升段弹道优化设计。张柳等[3]在此基础上组合了方向加速算法的运载火箭弹道优化算法,认为组合算法可避免传统非线性算法对初值敏感缺点,能大范围搜索具有全局收敛。洪蓓等[4]提出了有利于工程实现的主动俯仰程序角设计方法。熊伟等[5]提出了组合遗传算法和牛顿迭代法的运载能力优化,提高运算效率的方案。
本文提出了在约束残骸落区下的简化弹道优化方法,计算运载能力曲线,来解决不同构型论证工作中运载火箭的运载能力优化问题,大幅减少了计算工作量。同时,分析了在固定落区的情况下,不同加注规模对运载能力的影响,得出了定落区下的运载能力优化过程曲面,提高了构型论证工作的效率,并通过对某新构型运载火箭的定落区运载能力分析,验证了该方法的可行性和正确性。
1 弹道计算的数学模型
1.1 动力学模型
建立在发射坐标系下的火箭上升段弹道三自由度质点动力学方程[6]为
(1)
(2)
(3)

1.2 飞行程序角模型
飞行程序角在文献[3]的基础上进行一定的修改,公式分为3部分:垂直起飞段、重力转弯段、上升段。其中前两段的飞行程序角如下
(4)
式中,α为攻角,θ为弹道倾角,ωz为地球旋转角速度在发射坐标系z轴方向的分量,t1为垂直段飞行时间。则攻角α的公式见式(5),式中的αM为迭代参数
α=4αMea(t1-t)(ea(t1-t)-1)
(5)
根据式(4)、式(5)得知,在重力转弯段,攻角α的曲线由关机点的程序角终值迭代αM得出。
重力转弯段结束后,上升段程序角为
(6)

1.3 火箭弹道设计方法

具体而言,火箭从起飞到入轨的轨道设计过程中,首先需要估计一个火箭重力转弯段结束时的俯仰程序角终值φ0,以此来确定本轮次迭代时上升段的控制变量初值;然后构建上升段的控制参数与目标轨道参数的迭代关系,并进行迭代设计,具体流程如下:
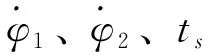

(7)
(8)
具体思路是通过对控制变量的摄动来分析各个控制变量对入轨参数的影响,因此当偏差量达到要求时,该组控制变量即可满足目标轨道要求。在计算过程中,需要关注重力转弯段程序角终值φ0对运载能力的影响。φ0决定了上升段控制变量的初值,可以对其进行梯度寻优。不同初值情况下的火箭程序角曲线如图1所示,对应运载能力如图2所示。
图1和图2为某构型火箭在残骸落区无约束的情况下进行阶梯寻优的过程数据,分别是一级结束时程序角φ0对后续工作段程序角及最终运载能力影响。
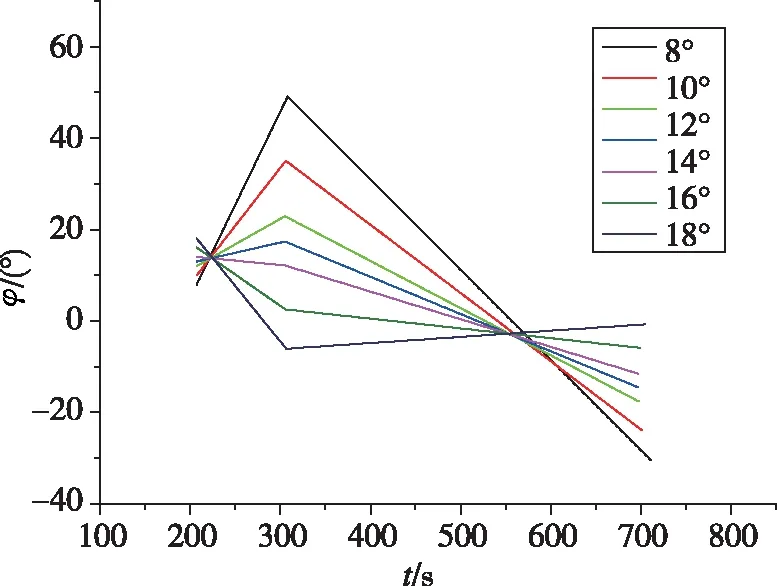
图1 不同φ0对后续程序角的影响Fig.1 Different φ0 values affect the subsequent program angle

图2 不同φ0对应200km最优LEO运载能力Fig. 2 Different φ0 values correspond to the optimal capacity of 200km LEO
由上述分析可见,在给定不同的φ0情况下,火箭运载能力明显具有最高点,因此可以使用梯度法对φ0进行寻优,即可找到该火箭构型的最优运载能力。但需要注意的是,有残骸落区约束也会对程序角φ0产生限制。
2 残骸落区对程序角的限制分析
火箭残骸的轨迹计算公式[7]为
(9)
(10)
可见,由于没有推力,残骸的最终射程完全依赖于分离时的速度、位置参数。
由于目前火箭都属于多级动力,因此往往设定转弯段完成时间为火箭第一次分离时间。通过1.3节对转弯段程序角终值对后续的轨道影响分析,可以得到转弯段程序角终值φ0是上升段的重要迭代变量的结论,结合式(9)、式(10)可以得出结论:φ0不仅决定了后续上升段的火箭轨道,也同时决定了火箭分离后残骸的最终射程。
在不同的φ0情况下,火箭残骸落点射程曲线如图3所示。图3为某构型火箭在落区无约束的情况下,一级结束时程序角φ0对一级残骸落点射程影响。

图3 不同φ0对应残骸落点射程Fig. 3 Different φ0 values correspond to the optimal point range
由图3可见,火箭残骸落点射程与φ0接近于线性相关,可以得出结论:若火箭的发射点、落区已定,则同一构型火箭的飞行轨迹由于φ0受落区约束而唯一确定。
这带来的一个问题就是,在一定起飞推力规模的情况下,具有最优运载能力的火箭构型的残骸往往不能落入现有落区,而使用传统落区的轨道设计又使火箭的运载能力大幅下降。因此有必要在火箭构型论证阶段就开展落区适应性分析工作。
3 残骸落区对火箭构型的影响分析
我国发射场大多为内陆发射场,残骸落区必须避开人口稠密地区、铁路、城市等重要设施,现内陆经济发展迅速,因此找到适合运载火箭的落区有一定难度。即便是文昌发射场也要面临着落区位于九段线内和跨过菲律宾的要求,需要选用目前已有落区或可行的新落区。
构型论证中,调整推进剂加注量,贮箱及外形尺寸会跟随改变,可根据结构效率比考虑结构质量变化。
某无尾翼两级构型运载火箭在不约束落区时最大运载能力为8350kg,若采用射程为1235km的某现有落区作为约束,则落区约束后的最优构型论证过程如下:
1)在原最优构型下,完成增加落区约束后运载能力计算。
2)分析一级加注量、二级加注量(结构效率比考虑结构质量变化)和φ0参数对残骸落点影响,如表1所示。
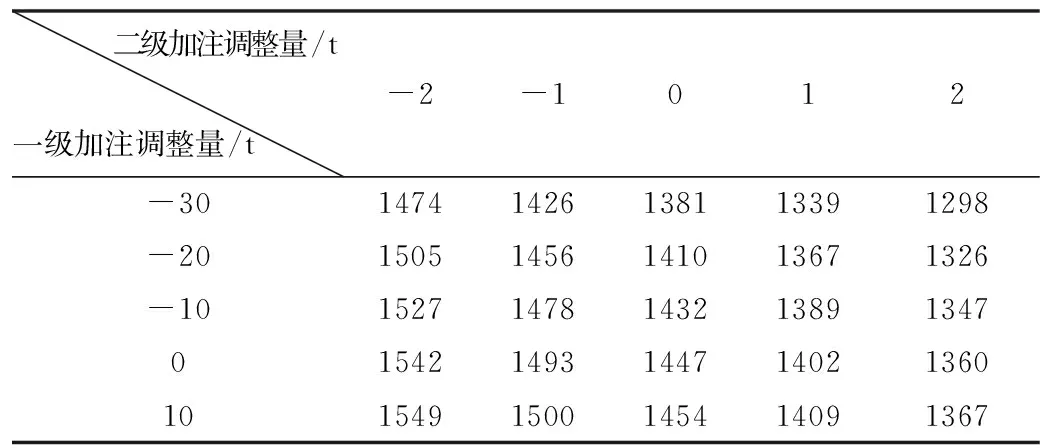
表1 一级结束程序角φ0相同、调整级间比下残骸落点射程 km
表1是一级结束程序角φ0相同,调整级间比获得残骸落点射程数据。由表1可以看出:火箭残骸落点射程随本级加注量增大而增大,随上面子级加注量增大而减小。
构型不同φ0对残骸落点影响如图3所示。
因此,可以认为两级火箭在有落区约束情况下,寻找最优运载能力构型是在三维空间内寻优过程。
3)残骸落区约束的火箭构型优化设计
考虑残骸落区约束的运载火箭构型优化设计是一个复杂约束下多变量强耦合的极值问题[8],火箭的各级级间比设计以及飞行程序角选择不仅决定运载能力的大小,同时也直接影响火箭残骸落区。在火箭构型复杂、参数众多的情况下,手动调整总体和弹道参数进行构型论证变得极为困难,可以通过弹道优化程序开展基于落区约束下的火箭构型优化论证。
优化过程如图4所示,首先通过选择待优化参数及其取值范围、目标变量和约束条件;优化过程中,总体参数计算根据各级级间比计算各级加注量;然后根据结构系数计算结构质量,得到弹道设计需要的参数后,自动更新到弹道设计文件中;再用弹道设计及优化程序开展弹道优化设计,直至收敛得到运载能力最优值。
以残骸落区为约束,对一级、二级加注量、重力转弯结束程序角φ0这3个优化变量进行优化分析,运载能力优化结果如图5、图6所示。
图5为残骸落区约束后,相对落区无约束最优构型下一级、二级加注调整量与运载能力关系三维曲面图。图6为三维图的俯视图,能直观看出约束落区后级间比优化下最优运载能力构型。

图4 弹道一体化优化流程图Fig.4 Optimized flow chart of trajectory design

图5 残骸落区约束后加注量与运载能力关系三维图Fig.5 Three-dimensional diagram of the relationship between capacity and propellants after restricting impact point

图6 三维图俯视图Fig.6 Top view of three-dimensional diagram
通过图5和图6看出,运载能力明显呈弧面,具有最高点。残骸落区约束后,原来落区无约束的最大运载能力构型运载能力不再最优,降低到了7769kg。需调整级间比及加注量并重新进行构型调整及运载能力分析。经过数据分析,在不同推进剂加注组合的情况下,能够清晰地得到最优点,为一级推进剂少加10t、二级加注量不变情况下的构型,对应的运载能力为7780kg。相对残骸落区无约束构型的计算结果,最大运载能力下降近570kg,但起飞规模方面要优于落区无约束构型。
4 结论
本文针对某一种构型运载火箭有无残骸落区约束的构型论证过程进行分析,梳理出火箭总体参数及弹道关键参数对落区的影响关系,开展了基于落区约束火箭构型的总体方案优化,发现落区约束后构型运载能力大幅降低,甚至出现运载能力不如起飞规模更小的火箭的情况,充分说明了残骸落区对构型论证的影响,因此,残骸落区的选择是在运载火箭构型设计时必须首要考虑的设计因素。

