面向临近空间高机动目标的改进预测命中点规划方法

尹中杰，刘 凯

(大连理工大学航空航天学院，大连 116024)

0 引言

近年来，随着高超声速技术的发展，以美国为代表的军事大国正在大力发展临近空间高超声速武器，并相继完成了一系列的飞行试验[1-7]，如X-43A、X-51A、HTV-2等，同时还提出了武器化的HSSW、AHW等项目，以及SR-72高超声速平台项目。2018年10月，美国陆军太空与导弹防御司令(SMDC)披露，将与美国空军、海军和导弹防御局合作研制一型高超声速滑翔飞行器，其中美国空军和陆军分别计划在2022年前列装“高超声速常规打击武器”(HCSW)和“远程高超声速武器”(LRHW)。

由于高超武器带来的威胁，相应的拦截方案研究受到了各国的重视，而预测命中点设计更是因为计算时间长受到广泛关注。预测命中点是攻击弹、拦截弹同时间到达的一点，预测命中规划是指在拦截弹发射前，通过算法计算出合理的拦截点，并为拦截弹装订相应的诸元，使得拦截弹准时精确地飞抵预测命中点的工作。为了完成预测命中点的设计，国内外学者普遍采用基于标准弹道[8-16]的预测命中点规划。

基于基本弹道的预测命中点设计是指拦截方提前通过对所有可以覆盖的区域，绘制标准弹道族，并通过调整拦截弹发射方位角形成等时间拦截曲面，并结合攻击方弹道寻找时间相同、位置重合的相遇点。该计算方法可以针对不同类型的目标飞行器快速有效地寻找准确的预测命中点。

由于需要拦截弹与目标飞行器同一时间到达相同地点，所以解算拦截时间就是问题的关键。李辕等[8]、张建祥等[9]、尤刘球[10]提出了以航程或拦截弹状态参数作为输入迭代相遇时间的方法。在此基础上， 张荣升等[11]通过以斜距为输入进行时间迭代，获得拦截弹与目标斜距相同的时间点，从而获得相应的拦截弹弹道。但是高超武器机动性强，弹道形式复杂，预测弹道上可能存在多个斜距相同的点，仅通过斜距无法描述预测命中点的信息，可能导致拦截失败。而且由于算法原因，标准弹道族要逐一时间、逐一弹道与目标进行位置比对，耗时较多。

随着拦截任务的明确与优化算法的应用，标准弹道族也可以根据所需的性能指标，进行有针对的设计。盛永智等[13]首先对拦截任务进行分析，并针对不同战场情况提出了相应的性能指标。在此基础上，谢经纬等[14]针对不同作战需求设计了不同类型的标准弹道族，大体分为考虑拦截时间需求的标准弹道族与考虑效费比的标准弹道族，并根据防御方探测系统首次捕获到目标的时间选取针对相应需求的标准弹道族，从而提高拦截效率。但是上述算法均只考虑了当前时刻的预测命中点规划问题，并没有对发射时间窗口计算问题进行深入研究，具有一定的局限性。

针对以上问题，本文采用建立标准弹道族结合斜距单调化与时间搜索算法的方式解决因机动造成的目标飞行器与拦截阵地斜距非线性存在多个斜距相同点，导致获得错误预测命中点的问题。利用拦截弹标准弹道族的物理特性增加判断条件，降低计算量，解决运算耗时长的问题，利用状态转换的思想设计发射时间窗口计算方法，从而快速准确完成预测命中点设计与发射时间窗口计算工作。

1 拦截弹动力学建模与问题描述

1.1 质点动力学模型

模型考虑地球自转、球形大地假设，在发射坐标系下建立拦截弹质点动力学模型，根据拦截弹的特性完成坐标系的转化、受力分析并建立动力学方程。

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

h=r-R

(9)

(10)

式中，x、y、z为发射系x、y、z轴位置，Vx、Vy、Vz为发射系x、y、z轴速度，θ、σ为发射系下弹道倾角、弹道偏角，D、L、Z、P分别为阻力、升力、侧向力、推力，Mfv为发射系与速度坐标系的转换矩阵，h、r分别为高度、地心距，m为拦截弹质量，g0为地表重力加速度，Re为地球半径，ωe为地球自转角速度，ωex、ωey、ωez为发射系下地球自转角速度分量。

1.2 问题描述

预测命中点是预先计算来袭目标和拦截弹的飞行弹道, 确定出瞬时遭遇点, 即预测命中点, 当预测命中点确定后，就导引拦截弹向其接近。

基于此，预测命中点规划问题可以描述为：结合预报弹道与标准弹道族，通过搜索算法寻找满足时间约束、位置约束的拦截点。并为拦截弹装订相应的诸元，确保其准时精确到达拦截点，如图1所示。

图1 拦截示意图Fig.1 Interception schematic

约束条件如下：

x(tf)=xtf
y(tf)=ytf
z(tf)=ztf

(11)

其中，tf为预测飞行时间，xtf、ytf、ztf为预测命中点在发射坐标系下的位置。

考虑到拦截过程有延迟发射的需求，需要计算发射时间窗口。发射窗口是指在基于当前标准弹道族，即使推迟发射，依旧存在预测命中点可行解的时间区间。

基于此，时间窗口计算问题可以描述为：结合目标预报弹道与标准弹道族，通过搜索算法获得可发射拦截弹至预测命中点的延迟时间区间。

2 预测命中点规划

2.1 现有方法的问题

现有方法普遍基于拦截阵地与目标之间的斜距进行时间的迭代，通过假设目标飞行器与发射阵地斜距是不断缩小，选取时间t0，将目标飞行器与发射阵地斜距ra与拦截弹斜距rd相对比，若ra>rd则t0增加，反之减小，通过迭代的方式获得ra=rd的时间t1，从而获得相应的拦截弹弹道。而高超声速飞行器会因为多种因素，导致距离拦截阵地的斜距不单调，即弹目距离不断缩小的假设不成立。此时基于上述原则的时间迭代方向可能存在错误，这使得依靠现有方法解算预测命中点时，存在即使有可行解却搜索不到的问题。

当目标飞行器基于感知信息发现拦截阵地，会通过机动远离拦截阵地，当离开拦截阵地一定距离后再次修正航向。这就导致预测弹道上存在若干斜距相同的点的情况，使得目标飞行器与拦截阵地的斜距时而降低，时而增加。此时如果仅仅考虑斜距ra=rd，依旧采用ra>rd则t0增加，反之减小的迭代原则，可能会导致在时间迭代跳入斜距单调递增的区间后，被提供了错误收敛方向，在迭代达到上限后，输出错误的预测命中点，导致拦截失败，如图2所示。

图2 斜距非单调示意图Fig.2 Diagonal non-monotonic sketch

除此之外，目标飞行器的打击目标不在拦截阵地的覆盖范围内，目标飞行器弹道穿过拦截阵地覆盖范围。此时必然存在两个以上的斜距相同的点，致使斜距不单调，这同样会导致预测命中点计算错误。

基于以上问题，这里提出了拦截时间区间的思想，将目标与拦截阵地之间的斜距进行单调化处理，确保在拦截区间内任意特定斜距只存在唯一解，来解决斜距解算无法收敛到正确解的问题。

2.2 标准弹道族设计

标准弹道设计采用目前工程规划方法中典型的多级运载火箭上升段指令生成规律进行设计。该方法将火箭上升过程分为若干飞行阶段，每段设定固定的程序角变化率指令形式，而这些指令由有限个参数决定，根据任务需求预先进行优化得到这些参数及其对应程序指令，装订在助推器系统中，上升段飞行过程中利用姿态控制系统实现程序指令即可。为寻求弹道轨迹的快速生成，将整个上升段分为3段，包括垂直上升段(0-T11)、负攻角转弯段(T11-T12)、重力转弯段(T12-T13)。

(1)垂直上升段

(12)

式中，1/v0为推重比。

(2)负攻角转弯段

在转弯段中，T11到T12为负攻角转弯段，如图3所示。在之后的大动压段一般依靠重力的法向分量缓慢的转弯，即重力转弯段(T12～T13)。

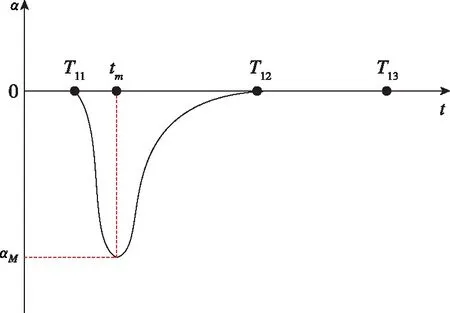
图3 攻角变化规律曲线Fig.3 Angle of attack variation with time

在负攻角转弯段中，根据实际要求，攻角变化规律可以由经验公式给出

α(t)=-αm·sin2f(t)

(13)

(3)重力转弯段

此段内程序攻角为0°，拦截弹全程飞行俯仰角近似公式为

(14)

当确定了T11、T12、T13，所选取的拦截弹弹道控制变量就可以确定为助推段负攻角大小和发射方位角。

由此，以拦截阵地为原点(0，0，0)在最大负攻角区间αm∈[αmmin,αmmax]中，每隔Δα积分标准弹道，再由tmin开始，将隔条拦截弹道中时间为tmin的点连接，构成等时间线，等时间线遵守tmin至tmax每间隔Δt连接一条的原则。由此可以获得完整的标准弹道族，如图4所示。

图4 标准弹道族Fig.4 Standard trajectories collection

2.3 目标飞行器拦截时间段划分

为解决不同时间、斜距相同的问题，需要对目标飞行器进行拦截区域划分，并分段讨论。

首先，获得斜距与时间的关系，确定一定时间内的斜距极值点个数n与相对应的时间tn，由此将拦截时间分为n+1段，时间段为t∈[ti-1,ti],i∈[0,n+1]，由此确保在规定时间段内，斜距变化是单调的，不存在斜距相同的可能，如图5所示。

图5 目标飞行器与拦截阵地斜距-时间图Fig.5 Range-time diagram of target vehicle and interception position

2.4 基于搜索算法的预测命中点计算

通过对拦截时间的划分可以确保在对应的时间段内，目标飞行器与拦截阵地的斜距是单调递增(递减)的，可以通过t时刻，目标飞行器的经纬度与高度与拦截弹的经纬度与高度是否相同来迭代预测命中点时间t与发射方位角af。但是由于拦截弹的发射方位角度af∈[0,360]，负攻角α∈[αmin,αmax]，产生的标准弹道族巨大，所以逐一时间、逐一标准弹道进行对比是不现实的，需要利用标准弹道族的物理特性基于新的搜索算法进行预测命中点搜索，提高运算效率。

拦截弹的可控变量有3个，分别是拦截弹的最大负攻角、发射方位角、飞行时间。最大负攻角与飞行时间共同决定了拦截弹的飞行高度、飞行距离，发射方位角决定拦截弹的飞行方向。其中飞行方向只与发射方位角有关，但是剩余两项存在耦合现象。

因此，搜索算法可以在标准弹道族中先筛选满足水平航程的拦截时间区间[tmin，tmax]，再根据目标飞行器的飞行高度在拦截时间区间[tmin，tmax]，及负攻角区间[αmin,αmax]中搜索满足高度条件的飞行时间tf及负攻角α，最后利用tf时刻的目标飞行器位置确定发射方位角af，确定拦截弹的飞行轨迹，从而装订发射诸元。

根据拦截条件可知，只有全部满足高度、水平航程、飞行方向条件的拦截弹才具有拦截的能力，缺少任意条件均无法有效拦截。但是一次性完成3个条件的筛选，算法过于复杂，所以可以率先筛选出满足水平航程的拦截时间区间作为拦截时间估计区域，并在后续步骤中进一步筛选符合高度条件的时间点，确定最大负攻角，最后计算发射方位角。具体步骤如下：

(1)初步估计时间区间[tmin，tmax]

根据拦截弹的物理特性可知，相同时间内，最大负攻角最大的拦截弹轨迹水平航程最大，则通过搜索最大负攻角最大的拦截弹道与目标弹道中同一时刻水平航程误差最小的点，就可以获得tmin。

假设初始飞行时间为t1，并通过目标飞行器预报信息计算出该时刻的发射方位角，同时获得t1时刻的目标飞行器与拦截阵地的水平距离La1、t1时刻最大负攻角最大的拦截弹水平距离Ld1，误差为ΔL1；获得拦截弹拦截窗口终端t3时刻的目标飞行器与拦截阵地的水平距离La3、t3时刻最大负攻角最大的拦截弹水平距离Ld3，误差为ΔL3；获得中间时刻t2的目标飞行器与拦截阵地的水平距离La2、t2时刻与最大负攻角最大的拦截弹水平距离Ld2，误差为ΔL2。

这里分为4种情况，并设计搜索算法：

① ΔL1>0, ΔL3>0时，说明该时间区域内没有拦截的可能，搜索结束。

② ΔL1<0, ΔL2<0时，说明该时间区域内没有拦截的可能，搜索结束。

图6 时间搜索示意图Fig.6 Time search diagram

确定了tmin，即可利用tmin，缩小tmax的搜索范围。同理，相同时间内，最大负攻角最小的拦截弹轨迹水平航程最小，则通过搜索最大负攻角最小的拦截弹道与目标弹道中同一时刻水平航程误差最小的点，就可以获得tmax。

假设初始飞行时间t1=tmin，并通过目标飞行器预报信息计算出该时刻的发射方位角，同时获得t1时刻的目标飞行器与拦截阵地的水平距离La1、t1时刻最大发射倾角的拦截弹水平距离Ld1，两者误差为ΔL1；获得拦截弹拦截时间区域终端t3时刻的目标飞行器与拦截阵地的水平距离La3、t3时刻最大负攻角最小的拦截弹水平距离Ld3，两者误差为ΔL3；获得中间时刻t2的目标飞行器与拦截阵地的水平距离La2、t2时刻与最大负攻角最小的拦截弹水平距离Ld2，误差为ΔL2。并再次利用二分法确定最大值tmax。

(2)标准弹道选取

由于前期的发射时间估计区域的确立，根据t∈[tmin,tmax]的目标飞行器的位置信息确定t时刻相对应的拦截弹发射方位角af∈[afmin,afmax]，根据目标飞行器的高度，确定与目标飞行器距离误差最小的负攻角α，存储t时刻ΔLt，最后选取t∈[tmin,tmax]中ΔLt最小的弹道作为拦截弹道。

具体流程图如图7、图8所示。

图7 筛选流程图Fig.7 Screening flow

2.5 发射时间窗口计算

由于拦截任务的需要，拦截弹可能需要延时发射，所以有必要计算出可行的拦截弹延时发射时间区间以及相关诸元。

由于攻击弹与拦截阵地的斜距可以转化为距离拦截阵地的水平距离与垂直距离，同理拦截弹与拦截阵地的斜距也可以转化为距离拦截阵地的水平距离与垂直距离。以水平距离为横坐标，垂直距离为纵坐标，不同标准弹道与预报弹道的交点就是可能的预测命中点。由于攻击弹到达可能的预测命中点的时间t4与拦截弹到达可能的预测命中点的时间t5是已知的，只要满足t4>t5就认为是可选的预测命中点。通过比较所有的可选预测命中点，得到最大的延迟时间Δt=max(t4-t5)，则获得拦截时间窗口t∈[0,Δt]，并通过t4时刻的目标位置计算出相对应的发射方位角af。

3 仿真分析

3.1 仿真输入

设目标飞行器初始飞行速度Ma=10，初始为平衡滑翔状态，60s～80s只进行纵向机动，80s～120s只进行横向机动。拦截阵地经纬度为(-3.9°，79.8°)，目标飞行器发现点经纬度为(-2.10°，80.58°)，满足预报精度误差的预报时间为120s，如图9所示。

图8 预测命中点及发射诸元解算流程图Fig.8 Flow charts for predicted impact point and launch data calculation

图9 目标轨迹图Fig.9 Trajectory diagram

3.2 预测命中点规划仿真分析

由于目标飞行器可能存在机动，所以斜距与飞行时间不是简单的线性关系，需要对目标预报弹道进行单调化处理，具体关系如图10所示。

图10 目标飞行器、拦截阵地斜距—时间图Fig.10 Range-time diagram of target vehicle and interception position

由图10可见，目标飞行器与拦截阵地斜距先降低后增加，所以发射窗口被分为两个区间，分别为t∈[0,90],t∈[90,120]。

在t∈[0,90]区间内，通过迭代发现在89s时，发射方位角为-35.73°，负攻角为-10.26°，预测命中点为(-3.6°，79.7°)，此时采用标称弹道的拦截弹与目标的预报位置误差为0.52km，可以通过后续的末制导环节进行修正，认为符合拦截条件，如图11所示。

图11 拦截示意图Fig.11 Interception schematic

在t∈[90,120]区间内，通过迭代没有发现满足当前时刻发射的拦截点，所以符合命中条件的预测命中点只有一个，为(-3.6°，79.7°)，计算用时0.2s。

3.3 拦截时间窗口计算仿真分析

通过对发射窗口计算，发现最大延迟时间为11s，发射方位角为-82.19°，负攻角为-12.25°,预测命中点(-3.9°，79.4°)，此时采用标称弹道的拦截弹与目标的预报位置误差为0.34km，同样可以通过后续的末制导环节进行修正，计算用时0.3s，如图12所示。

图12 最大延迟时间拦截示意图Fig.12 Maximum delay time interception diagram

针对抛物线弹道延迟发射诸元如表1所示。

由表1可知，由雷达首次发现目标的时刻至随后的11s内，随着拦截高度的降低，最大负攻角幅值变大。同时所有选取的时间节点均有拦截弹道可以准时飞抵预测命中点，可以认为在0s～11s这个拦截窗口内拦截窗口时间连续，所有的预测命中点均有标准弹道与其相对应。

表1 延时发射诸元表

4 结论

本文针对临近空间高机动飞行器机动能力强，所带来的弹道中存在多个斜距相同的点，导致基于斜距迭代预测命中点的方法不适用的问题，通过弹道划分的方法，保证了每个搜索区间的斜距具有单调性。在此基础上利用改进的快速搜索算法，准确有效地完成预测命中点规划与发射时间窗口计算。考虑高超声速飞行器预报精度差，所带来的更新后的预测命中点与原有预测命中点位置偏差较大的问题，未来将开展拦截弹道在线快速纠偏方法的研究，来弥补此方面的不足。