多维数值型敏感属性数据的个性化隐私保护方法
张梅舒,徐雅斌,3*
(1.网络文化与数字传播北京市重点实验室(北京信息科技大学),北京100101;2.北京信息科技大学计算机学院,北京100101;3.北京材料基因工程高精尖创新中心(北京信息科技大学),北京100101)
0 引言
随着信息技术的飞速发展,各个行业和领域都积累了大量的数据,而且数据规模正以惊人的速度增长[1]。大数据蕴含着巨大的商业价值,为了更好地利用大数据,数据共享势在必行。而在共享的海量数据中,往往涉及到个人信息或者敏感数据[2]。如果直接进行数据共享就可能会泄露个人隐私信息,因此,为了保证个人敏感信息的安全,在发布数据的同时应进行隐私保护[3]。
现有的数据隐私保护方法主要针对单一敏感属性的数据[4-6]。但是,在很多现实应用中,发布的数据往往涉及到多个敏感属性。对多敏感属性数据的隐私保护的研究主要是针对多维分类型敏感属性和单维数值型敏感属性数据,对多维数值型敏感属性数据的隐私保护研究少有涉猎。
事实上,多维数值型敏感属性数据更具一般性,对其进行隐私保护的研究不仅可以有效解决多维数值型敏感属性数据发布时的隐私泄露问题,还可以扩展数据的隐私保护范围,促进隐私保护研究的发展和大数据安全技术的进步。
杨晓春等[7]首次对多敏感属性数据发布问题进行了详细研究,继承了有损连接的思想,提出了针对多敏感属性数据进行隐私保护的多维桶分组(Multi-Sensitive Bucketization,MSB)技术,并提出了3 种不同的分组策略。金华等[8]改进了分组算法,提出了l-覆盖性聚类分组方法。杨静等[9]给出了一种基于值域等级划分的个性化定制方案,并提出了一种最小选择度优先的面向多敏感属性数据的l-多样性算法。
罗方炜等[10]提出一种(l,m)-多样性模型,该模型要求当同一敏感值的元组从等价类中删除时,剩余的元组仍满足独立敏感属性的(l-1,m)-多样性,这样能够有效抵制关联攻击,但是仍存在敏感值语义相近问题。Jia 等[11]针对敏感值语义相近问题提出了(l,m,d)-匿名模型,但该模型的数据损失较大。刘善成等[12]提出了一种基于敏感度的分组技术——(g,l)-分组方法,不仅解决了多敏感属性隐私数据发布的问题,同时还可有效抵制相似性攻击和偏斜攻击,但该方法的数据损失较大。Zhang 等[13]提出了MSA(α,l)算法,使分组后的数据满足l-多样性和α-最大约束,在一定程度上减少了数据损失。
李文[14]考虑了准标识符属性的数据质量和敏感属性的敏感程度,提出了基于主敏感属性的排序分组算法,可减少数据损失,提高数据可用性。
此外,还有一些基于k-匿名的算法。Wu等[15]提出p-覆盖k-匿名算法,可降低敏感属性泄露的风险。宋明秋等[16]在k-匿名模型实现的过程中,通过引入属性近似度概念,提出了一种多属性泛化的k-匿名算法。王秋月等[17]提出了一种多敏感属性分级的(αij,k,m)-匿名隐私保护方法。该模型为每个敏感属性的值进行分级设置,并为每个级别设置一个特定的αij,避免具有相同级别敏感值的记录被分在同一组中,从而可有效防止语义相似和关联攻击。
针对多维数值型敏感属性数据发布的隐私保护,刘腾腾等[18]提出了l-MNSA(l-Multi-Numerical Sensitive Attribute)算法,该算法使分组后的数据在每一维数值型敏感属性上的分布都比较均匀,能够防止相似攻击,但其不适合大数据。Liu等[19-20]提出了一种基于聚类和多维桶的数据隐私保护方法MNSACM,该方法在分组前将数值型敏感属性聚类,可以在一定程度上保护数值型敏感属性;但它没有考虑准标识符的质量,数据发布质量较低。陆洋[21]提出了一种基于聚类和加权多维桶分组的个性化隐私保护方法WMNSAPM。该方法利用加权多维桶的思想,实现了个性化匿名隐私保护的效果;但该方法没有考虑准标识符的质量,数据损失较大,而且需要由用户自己设置桶的权重,不仅难以实现,而且缺乏合理性。
综上所述,现有的针对多维数值型敏感属性数据的隐私保护方法存在以下问题:1)分组时仅考虑敏感属性的属性值,未考虑准标识符的范围,数据损失较大;2)提出的个性化隐私保护方法需要由用户设置桶的权重,对用户的专业性要求过高。
针对现有研究中存在的问题,本文提出如下设计方案:在数据预处理时,首先根据准标识符属性对数据集进行聚类,由此将一个数据集分成若干个准标识符属性值接近的子数据集,再根据数据的分布情况对数值型敏感属性进行聚类;然后,根据多维桶的容量和敏感属性的敏感程度计算加权选择度,并由此构建加权多维桶;在对数据分组时,优先考虑加权选择度大的桶中的数据,使分组后的数据满足多敏感属性l-多样性分布;最后,对分组后的数据进行匿名化处理。
本文工作如下:
1)根据准标识符的相似程度,将数据集划分成若干准标识符属性值接近的子集,由此可缩小数据集中准标识符的取值范围,有利于减少信息损失;
2)考虑到用户对于敏感属性的敏感程度不同,根据用户对敏感属性的敏感程度排序得到敏感属性的权重,将敏感属性的权重和多维桶的桶容量作为参数,提出一种加权选择度计算方法,有助于对数据进行个性化的隐私保护。
1 数据预处理
1.1 数据集聚类
研究发现,数据记录之间往往具有内在关系,尤其是当数据量较大时,某些数据记录在某个准标识符上具有相似的取值。为此可以通过聚类将具有较多共同特征的准标识符属性聚为一类,并由此将数据集分为若干子集,以减小数据的隐匿程度以及准标识符的泛化率,提高数据的可用性。
本文采用简单实用的k-means 算法根据准标识符属性值对数据集进行聚类。
由于准标识符属性既有数值型的又有分类型的,聚类时应作不同的考虑。对于数值类型的属性,数值差即为距离;对于分类型的属性,参考文献[12]提出的概化树,为每个属性构建概化树,通过概化树计算非数值类型属性的距离。例如workclass 属性的值域为{private,federal-gov,local-gov,stategov,sef-emp-inc,sef-emp-not-inc,withou-pay,never-worked},构建的概化树如图1所示。
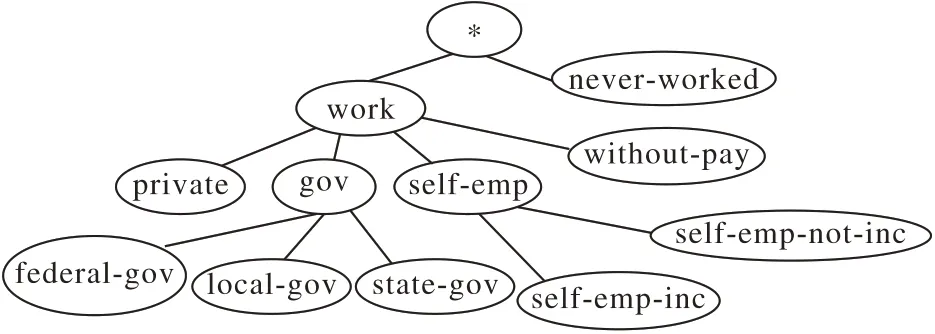
图1 workclass的概化树Fig.1 Generalized tree of workclass
概化树的每层都有个权值。例如,该泛化树总共四层,规定从上到下每层的权值分别为0、1、2、3。两个分类型数据之间的距离等于该两个节点到最小公共父节点的层次距离之和。例如,求federal-gov 和sef-emp-inc 之间的距离,需要先找到最小公共父节点work,由此两个值的距离可计算如下:
d(federal-gov,sef-emp-inc)=(3-1)+(3-1)=4
以一个精简后的人口普查数据集为例,其准标识符属性有age 和workclass,数值型敏感属性有profit 和hours-perweek。假定按照age 进行聚类,根据年龄段将数据集聚类,结果形成4个数据子集。其中的一个数据子集如表1所示。
1.2 数值型敏感属性值聚类
为了避免敏感属性值差异较小的两个值分别作为独立的桶,造成信息泄露,有必要对需要进行隐私保护的多个数值型敏感属性值分别进行聚类。
假设一个数据表中有n 条数据记录,该数据表包含m 维数值型敏感属性。将每一维数值型敏感属性值聚成多个簇,记作{Si1,Si2,…,Sij}(1 ≤i ≤m)。每个簇的属性值个数不一定相同,但所有的簇覆盖了这一维敏感属性的所有值。
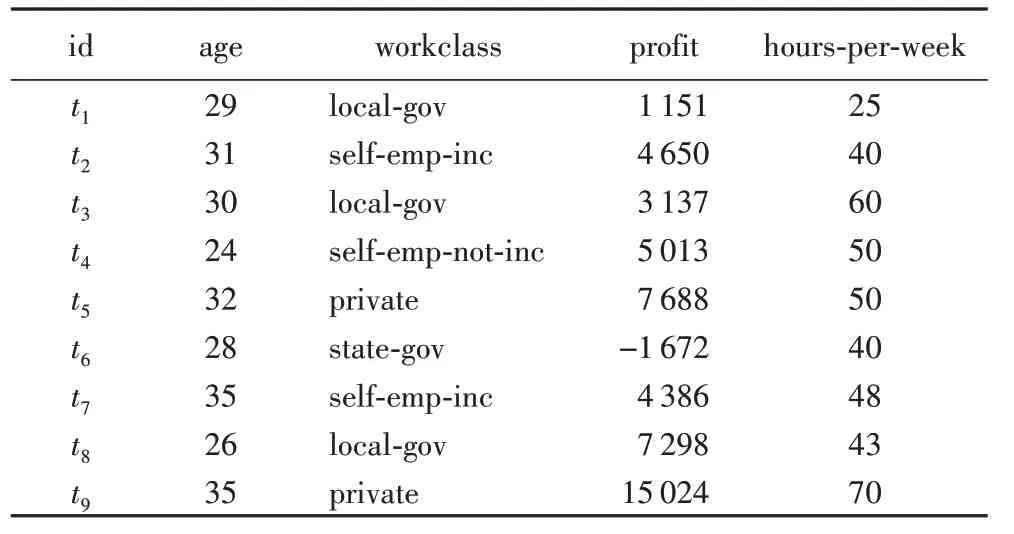
表1 聚类产生的一个数据子集Tab.1 A subset generated by clustering
本文同样采用k-means 算法对数据表1 中的数值型敏感属性profit(S1)和hours-per-week(S2)的属性值分别进行聚类,聚类结果分别为S1和S2:

聚类后使得同一个簇的属性值相近,不同簇的属性值差异较大,任意两个簇之间的交集为空集。
2 加权多维桶构建
构建加权多维桶的步骤如下:
1)构建多维桶。根据敏感属性profit(S1)和hours-perweek(S2)的值,对表1 中的数据进行映射,得到的多维桶分组如表2 所示。其中:每个单元格代表一个桶,空格说明该桶中不包含数据;t1~t9为表1中数据的id。

表2 多维桶分组Tab.2 Multi-sensitive bucketization
2)计算每个桶的加权选择度。基于多维桶的分组算法在进行分组时,一般只考虑桶的容量大小,然而,在实际应用中,如果某些元组中包含更重要的信息,就需要优先考虑。为此,本文为每个桶赋予一个加权选择度,由此构建一个加权多维桶。
对于加权选择度的计算,一般需要考虑敏感属性值的敏感程度、桶容量和语义相似度这三个因素。然而,由于数值型属性不存在语义相似的问题,并且属性值的敏感程度也没有明显的区别,为此,本文在计算加权选择度时,只需要将桶容量和敏感属性的敏感程度考虑在内即可。
加权选择度的计算步骤如下:
步骤1 获取用户对m 个敏感属性的敏感程度由大到小的顺序排列S1,S2,…,Sm,设定当前维的重要程度为S0,且S0>S1;
步骤2 利用层次分析法得到m 个敏感属性的权重分别为W1,W2,…,Wm,当前维的权重为W0;
步骤3 利用式(1)计算加权选择度:

其中:第i 个敏感属性的权重为Wi,第i 维敏感属性值与当前桶属于同一簇的记录数为Ci,桶容量为c。
对于表2 中的数据,假设用户认为敏感属性profit(S1)比hours-per-week(S2)更重要,即敏感程度S0>S1>S2。利用加权选择度得到权重分别为:W0=0.63,W1=0.26,W2=0.11。利用式(1)得到各个桶的加权选择度分别为:{1.26,1.33,2.48,1.59,1.63,1.37,1.26,1}。
3)给每个桶赋予相应的加权选择度,从而得到加权多维桶。
将计算得到的加权选择度赋给多维桶,最终得到的加权多维桶如表3 所示,其中,括号内的数字即为每个桶的加权选择度。

表3 加权多维桶分组Tab.3 Weighted multi-sensitive bucketization
3 数据分组及匿名化处理
文献[21]提出的WMNSAPM 方法中:首先将各维数值型敏感属性的属性值进行聚类;然后利用用户指定的权值构建加权多维桶,并将数据映射到加权多维桶中;接着通过基于加权的最大维容量优先贪心算法,构成满足l-多样性的分组;最后,将各个分组的准标识符进行匿名化处理。
该方法存在以下问题:
1)分组时没有考虑准标识符属性的范围,如果准标识符属性的范围过大,在匿名化处理时会过度泛化,导致数据损失度较大、可用性较低;
2)加权多维桶的权重需要用户设置,对用户的专业性要求过高,准确性难以把握。
针对文献[21]方法存在的问题,本文做了如下改进:
1)在分组之前根据准标识符属性的范围将数据集聚类,从而分成若干准标识符属性值接近的子集,然后分别对每个子集进行分组及匿名化处理,由此可缩小数据集中准标识符的取值范围,有利于减少信息损失。
2)在加权多维桶权重的计算时,根据用户对于敏感属性的敏感度的排序,利用层次分析法计算出敏感属性的权重,然后根据敏感属性的权重和多维桶的桶容量来计算出多维桶的权重。
本文方法的具体步骤包括:
1)根据准标识符属性的范围将数据集聚类,对得到的各个子集分别进行步骤2)~5)操作;
2)将各维数值型敏感属性的属性值进行聚类;
3)利用本文第2章提出的方法构建加权多维桶;
4)分组时优先选择加权选择度大的桶中的数据,将数据分成满足l-多样性的分组;
5)将各个分组的准标识符属性进行匿名化处理。
假设l取值为3,按照本文方法对表1中的数据进行分组,得到的结果为:{{t1,t2,t5},{t3,t7,t9},{t4,t6,t8}}。
最后,将分组后的数据进行匿名化处理:数值型数据取最值作为两个边界值,泛化为“最小值-最大值”;分类型数据将属性值的最小公共父节点作为泛化结果,得到的待发布数据如表4所示。
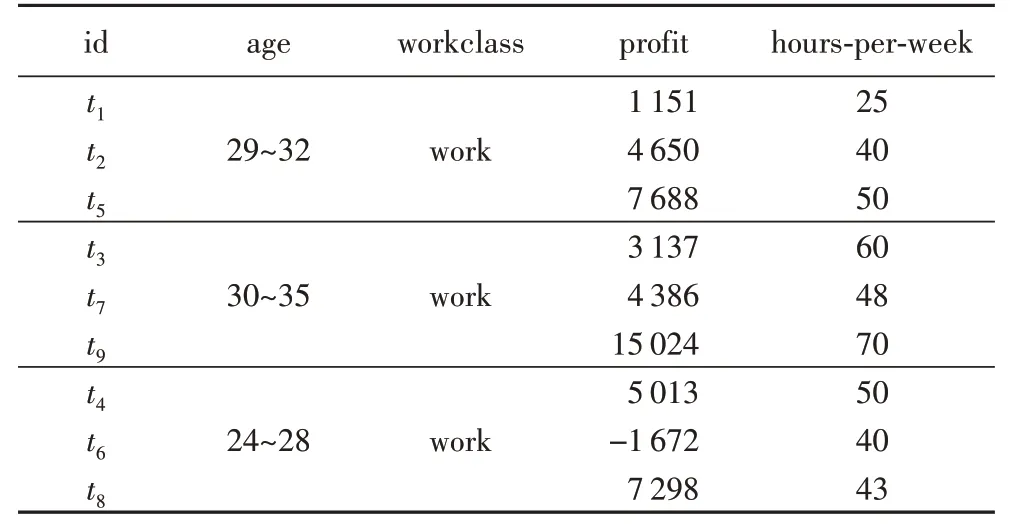
表4 待发布数据Tab.4 Data to be released
4 实验与分析
4.1 实验环境及数据集
实验所需数据采用UCI 机器学习中心的标准Adult 数据集,共有48 842 条数据,去除含有空值数据后的可用数据为30 162条记录,选取其中的8个属性进行实验。将其中的属性age、workclass、education、education-num、marital-status、sex 作为准标识符属性,将属性profit 和hours-per-week 作为敏感属性,属性描述见表5。
实验的硬件环境是Intel Core i7-4790 CPU@3.60 GHz,8.0 GB RAM,Windows 7 专业版操作系统,JetBrains PyCharm 2017.3 x64,算法的实现语言为Python3。
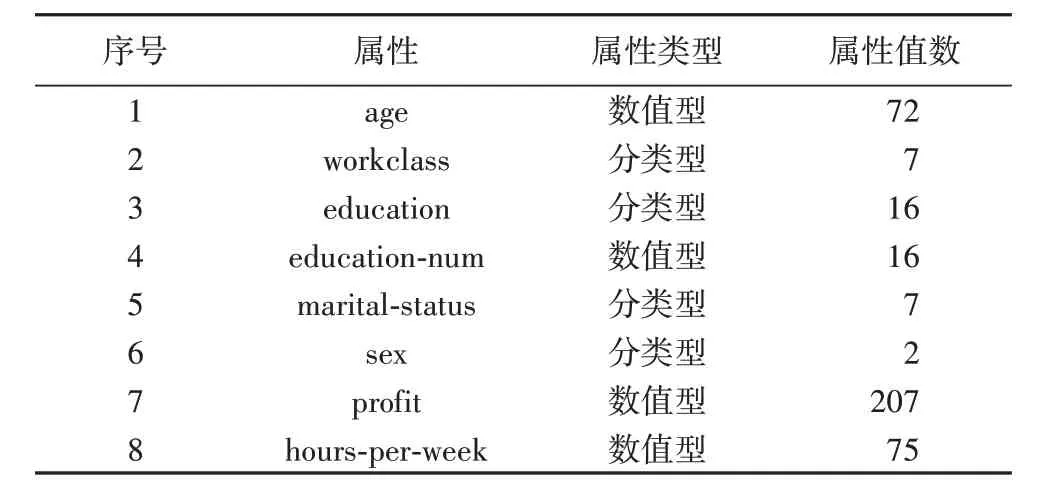
表5 实验数据集的属性描述Tab.5 Attribute description of experimental dataset
4.2 评价标准
1)信息损失度。数据分组后的匿名过程会对数据质量造成损失,降低数据可用性。数据质量的度量,主要针对准标识符被泛化的程度,常用信息损失度进行衡量。信息损失度越小,数据可用性越高。由于数据集中的准标识符属性既有数值型又有分类型,因此信息损失度的计算要考虑两种类型的属性。
定义1数值型属性的信息损失度(Information Loss of Numerical attribute,ILN)。
设Min和Max分别是一个分组的最小值和最大值,R表示整个数据表的值域范围,则:

定义2分类型属性的信息损失度(Information Loss of Classified attribute,ILC)。
给每个分类型属性构建概化树,p表示概化树中两个节点的最小公共父节点的高度,h 表示整个概化树的高度,Wi,j表示概化树i、j两个高度之间的权值,则:
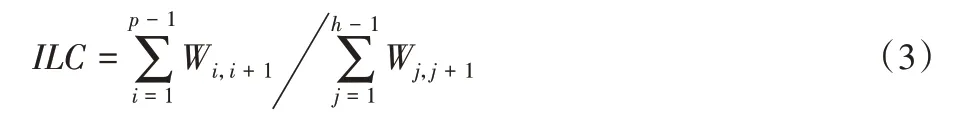
定义3分组信息损失度。
设N1,N2,…,NI,C1,C2,…,CJ是一个分组的准标识符属性,其中Ni(1 ≤i ≤I)表示数值型数据,Cj(1 ≤j ≤J)表示分类型数据,则整个分组的信息损失度IL(Information Loss)为各个准标识符属性的信息损失度之和,即:

假设数据表为T,处理后的分组数为M,则该数据表的信息损失度为所有分组的信息损失度之和,即:

2)隐匿率。
定义4隐匿率。隐匿处理的数据记录在数据表所有数据记录中所占的比例:

其中:t 表示隐匿的数据记录条数,|T |表示数据表总的数据量。隐匿率越小,发布的数据效果越好,理想情况下该值为0。
3)附加信息损失度。初次分组后,为了减少隐匿率,在满足l-多样性的前提下,将剩余的数据分到已有分组中。这样,在最终的分组中,某些敏感属性的值可能重复,即l <|G|(G 表示分组的数据记录数),这就在一定程度上增加了隐私泄露的风险,为此引入附加信息损失度来衡量这种风险。
定义5 附加信息损失度。设G{G1,G2,…Gi,…,Gm}是数据表T 上的分组,则附加信息损失度(Additional Information Loss,AIL)如下:

4)运行时间。算法的运行时间反映了算法的执行效率,是算法性能评价的一个重要标准。
4.3 实验结果及分析
在进行分组之前,需要对数值型敏感属性进行聚类。本文将profit 和hours-per-week 分别聚类为9 类和7 类。因此,算法中l-多样性的l的取值范围是2 ≤l ≤7。针对不同的l值,本实验分别用文献[19]的MNSACM 和文献[21]的WMNSAPM以及本文方法在相同的数据集上进行隐私保护处理,然后计算各个评价指标的值。
1)信息损失度分析。对于不同的l值,各个方法的信息损失度如图2 所示。由图2 可以看出,随着l 值的不断增大,3 个方法的信息损失度不断增加;在l 值相同的情况下,本文方法的信息损失度比MNSACM 和WMNSAPM 的更低,对应的数据可用性更高。分析原因如下:随着l 的增大,每个分组中的数据条数增加,分组中准标识符属性的范围增大,因而信息损失度增加。由于在分组之前,本文方法先根据用户需要的准标识符属性将数据集进行了聚类,避免了不必要的信息损失,因此,在l值相同的时候,本文方法的信息损失度更低。
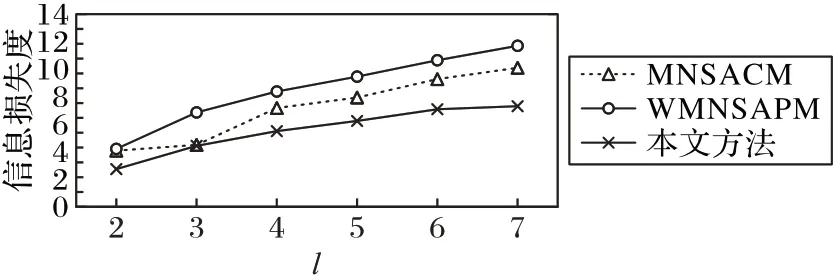
图2 不同算法的信息损失度随l值的变化Fig.2 Information loss degrees of different algorithms varying with l value
2)隐匿率分析。对于不同的l值,各个算法的隐匿率如图3所示。由图3可以看出,3个方法的隐匿率都随着l值增大而增大,当l 取值不超过4 时,本文方法与WMNSAPM 的隐匿率均较低,具有很好的性能;而当l 取值超过4 时,3 个方法的隐匿率都比较高。分析原因如下:随着l 值的增大,在分组过程中得到的分组数越少,被隐匿的数据越多,因而隐匿率越高。由于MNSACM 在进行初次分组后,没有对未分组数据进行二次分组,直接将其进行隐匿,所以,隐匿率更高。
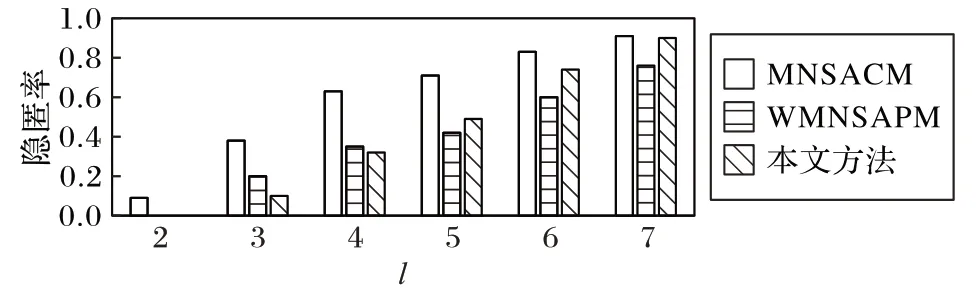
图3 不同算法的隐匿率随l值的变化Fig.3 Concealment rates of different algorithms varying with l value
3)附加信息损失度分析。由于MNSACM 没有对分组剩余的数据进行二次分组,不存在附加信息损失,因此,对于附加信息损失度的实验只考虑WMNSAPM 与本文方法。对于不同的l 值,两个算法的附加信息损失度如图4 所示。由图4可以看出,WMNSAPM 的附加信息损失度随着l的增大而不断增大;虽然本文方法的附加信息损失度也随着l 的增大而增大,但之后趋于稳定。分析原因如下:随着l的增大,初次分组得到的分组数越来越少,即剩余的未分组数据越来越多,因此二次分组的数据也越来越多,进而附加信息损失度越来越大。
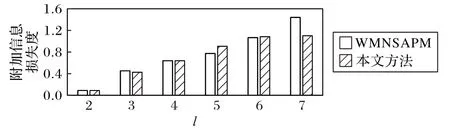
图4 不同算法的附加信息损失度随l值的变化Fig.4 Additional information losses of different algorithms varying with l value
4)运行时间分析。对于不同的l值,三个算法的运行时间如图5 所示。由图5 可以看出,MNSACM 和本文方法的运行时间在0~10 s,运行时间较短,效率较高。而且随着l 值的增大,本文方法的优势越来越明显,而WMNSAPM 的运行时间较长,效率较低。分析原因如下:MNSACM 没有对未分组数据进行二次分组,故运行时间较短;本文方法在分组之前将数据进行聚类,然后对每个簇分别进行分组处理,因而每个簇的数据相对较少,故运行时间较短。
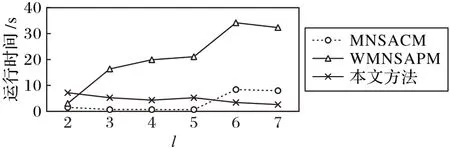
图5 不同算法的运行时间随l值的变化Fig.5 Running times of different algorithms varying with l value
5 结语
本文针对多维数值型敏感属性数据的隐私保护问题展开研究,在对已有方法进行分析的基础上,提出了一种个性化隐私保护方法。该方法首先根据准标识符属性对数据集进行聚类,由此减少了信息损失和隐私泄露风险;在计算多维桶的权重时,考虑到用户对敏感属性具有不同的敏感程度,将敏感属性的敏感程度和多维桶的桶容量作为参数,得到桶的加权选择度;在将数据分组时,选择加权选择度最大的桶中的数据,使得分组中的多敏感属性满足l-多样性。
实验结果表明,相比现有方法,采用本文提出的方法对多维数值型敏感属性的数据进行隐私保护,具有较低的信息损失度和较短的运行时间,提高了数据质量和运行效率。

