结合梯度投影稀疏重构和复数小波的图像重构

高彦彦，李 莉，张 晶，贾英茜

（石家庄学院机电学院，石家庄050035）

0 引言

近些年被人们广泛关注的图像压缩感知是由David L.Donoho 在稀疏表示和优化理论的基础上提出的一种成像理论［1］，其本质就是在对信号进行随机投影得到维数远小于原始信号的观测值后，利用信号在某一变换域的稀疏性，通过求解一系列的线性或者非线性的解码模型，得到原始信号的逼近。这种成像方法在数据采集端实现了采样与压缩的同步进行，因而极大地缓解了采集端的压力。这样就可以利用少量的传感器或传感器阵列采集信息，通过复杂的重构算法重建高分辨率图像，已应用在诸多方面［2-5］，图像重构是典型应用之一。

基于压缩感知的图像重构有多种算法［6-7］，这些算法主要是利用信号在某一表示域的稀疏性，通过解决不同形式的优化问题来得到信号的最优逼近，文献［8-9］对压缩感知中涉及的相关内容进行了综述。

信号在某一变换域的稀疏度是指变换系数中非零元素的个数，这可以用系数的l0范数表示。一般来说由于自然信号的稀疏性或是可压缩性，使得信号在某一变换域存在稀疏解或近似的稀疏解，因而压缩感知重构的目的就可以看成是寻找信号的最小稀疏解的过程，即：最小化系数的l0范数的过程。但是这是一个NP-hard 问题，不易求解，因而可以将l0范数转化为其他函数的最小化问题。文献［10］中将l0范数转化为l1范数最小化后，利用基追踪进一步将其转化为线性规划问题进行求解；也可以根据文献［11］提出的迭代收缩算法，利用前一估计值和变化域的阈值处理得到迭代更新值，进而逼近最优解；匹配追踪［12］是一种常用的贪婪算法，主要就是在每一步迭代中寻找投影字典中最匹配的原子，从而缩小剩余量，这种算法的计算量过大，对于图像压缩感知不是很好；文献［13］中利用图像的全变差（梯度稀疏性，变换系数的稀疏性可以看成是梯度的一种跳变）结合凸集投影和小波阈值处理完成了图像的压缩感知重构。在以上介绍的这些方法中，均需要对投影矩阵A 进行准确处理，而文献［14］针对稀疏重构提出的梯度投影（Gradient Projection for Sparse Reconstruction，GPSR）算法则不需要对投影矩阵A 进行准确的处理，只需要计算A与AT的内积，简化了算法。

压缩感知中变换域的选择目前常用的是正交小波，但正交小波存在一些不可避免的缺点：振荡、平移变性、方向选择性差。Kingsbury［15］提出的双树复数小波变换（Dual-Tree Complex Wavelet Transform，DT CWT）克服了这些缺点，具有平移不变性和良好的方向选择性。为了提高压缩感知重构算法的有效性，本文在利用置乱离散余弦变换（Permute Discrete Cosine Transform，PDCT）得到观测值后，利用图像在双树复数小波域的稀疏性，结合GPSR 算法完成了图像压缩感知重构，并通过实验验证了该算法的有效性。

1 压缩感知

原始信号s ∈Rn，随机投影过程表示为y=Φs，Φ ∈Rm×n定义为随机投影矩阵，y ∈Rm（n ≫m）。压缩感知重构的目的是利用信号在某一变换域（用Ψ 表示）的稀疏性，从远少于n的m个观测值中恢复原始信号。对于这一问题需要保证Φ满足Candes等提出的限制等容性，并且Φ与Ψ不相关［16］。

对于一维信号，随机矩阵Φ 通常情况下选择高斯随机阵［17］，但是对于二维图像，这种随机矩阵是不可取的，本文选择PDCT（将图像进行一维置乱，再转为二维图像进行离散余弦变换），从得到的变换系数中选择一定数量的数值作为观测值y。

压缩感知的重构主要就是利用图像变换系数的稀疏性来进行的，需要找到最稀疏的变换系数。矩阵的稀疏性可以用其l0表示，但是对l0问题的求解并不易得到，因而可以将其转为l1问题：

s.t.y=Φs

其中，α 是图像的变换系数，用α=Ψs 表示。对于式（1）所述优化问题，通常情况下考虑：

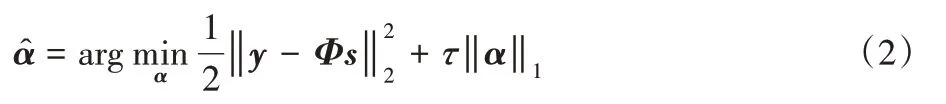
其中参数τ 为非负值，用于平衡式（2）中的前后两部分的比重。由于α=Ψs，将s=ΨTα代入式（2），得到：

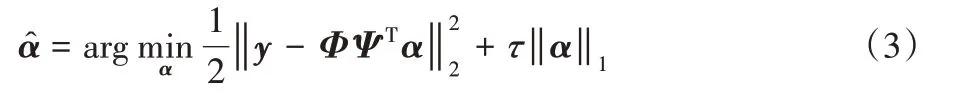
设A=ΦΨT，x=α，则式（3）变为：

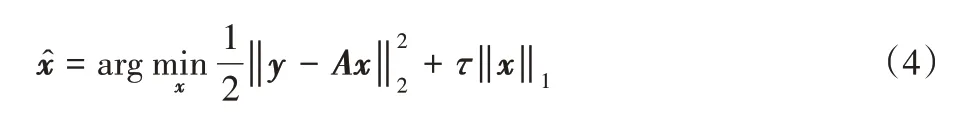
2 针对稀疏表示的梯度追踪算法

GPSR算法［15］首先将式（4）代表的问题转化为边界约束二次问题：

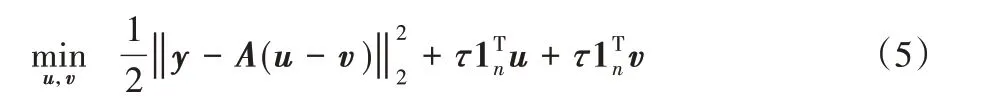
s.t.u ≥0，v ≥0

其中u、v分别表示x的正负两部分，即：

则 ui，j=(xi，j)+=max(0，xi，j)，vi，j=(-xi，j)+=max(0，-xi，j)，i，j=1，2，…，n。由 此 得 到，其 中 1n=[1，1，…，1]T。

将式（5）进一步整理写成标准的边界约束二次问题形式：

s.t.z ≥0

对于给定的向量z=[uT，vT]T，存在：

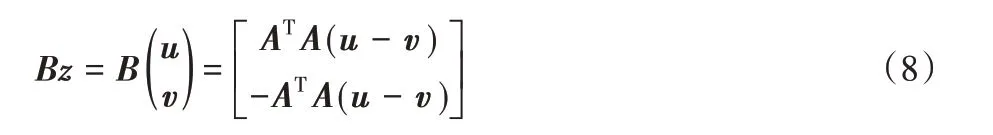
由式（7）可得函数F(z)的梯度：

式（9）又可以表示为∇F(z)=(∇u，∇v)T，根据式（5）可以得到：

梯度投影算法的主要步骤：

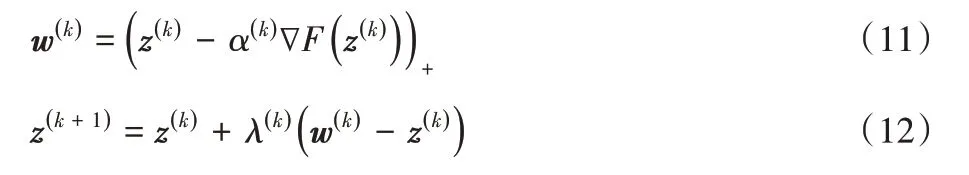
进一步推导，将其转化为以u、v作变量的形式：

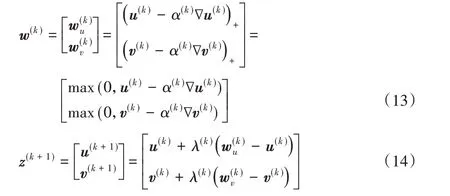
GPSR-Basic算法对应的是λ()k=1，此时式（12）变为：

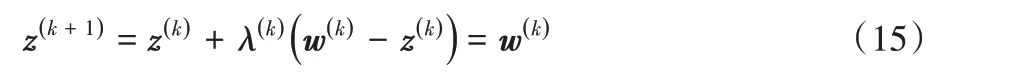
在GPSR-Basic，标量参数α(k)的初始值［8］设为：

其中向量g(k)具体表示为：

GPSR-Basic的具体步骤为：

1）初始化：设x(0)初始值为0，根据式（6）得到u(0)与v(0)，并且由式（5）计算目标函数f(0)。

2）根据式（10）计算得到∇u(k)与∇v(k)，进而得到∇x(k)=∇u(k)-∇v(k)。

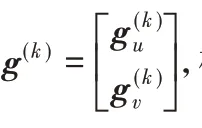
4）α(k)=α0。

5）根 据 式（13）、（14）得 到u(k+1)与v(k+1)，从 而 得 到x(k+1)=u(k+1)-v(k+1)，计算f(x(k+1))。

6）判断下式是否成立：

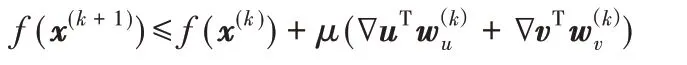
如 果 成 立，进 入 下 一 步；否 则α(k)=βα(k)，返 回 步 骤5），β ∈(0，1)。

7）判断是否停止迭代：根据目标函数的变化情况进行判断，即是否成立，成立终止迭代，否则返回步骤2）继续进行。

GPSR-Basic 与文献［14］中考虑Barzilai-Borwein 梯度策略的算法GPSR-BB 的不同之处在于标量参数α(k)与λk的设定，后者的参数设定如下：

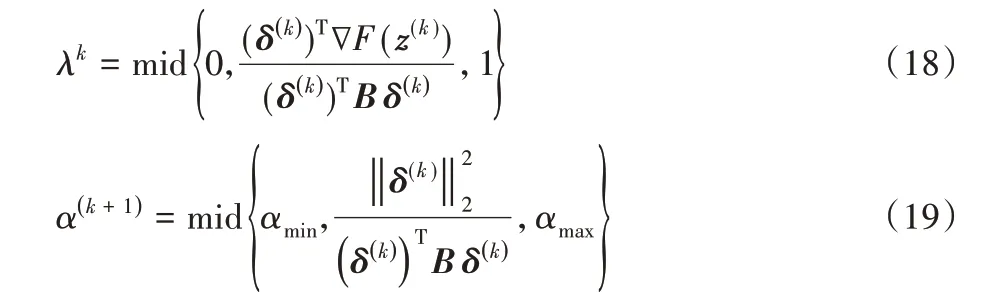
3 图像重构的实现

本文压缩传感系统是利用图像在双树复数小波变换域的稀疏性，并结合GPSR算法实现图像重构。

DT CWT 是利用四个普通的离散正交小波实现的，其变换系数包括四个支路，分别对应实部和虚部两部分，每一部分又分为上下两个支路。DT CWT 克服了正交小波的缺点，具有近似的平移不变性和良好的方向选择性。如图1（a）所示，DT CWT 具有6 个方向（°±15°，±45°，±75°），而普通的正交小波只具有3个方向（0°，45°，90°），如图1（b）所示。由图1可以看出，和普通正交小波相比，DT CWT不具有振荡特性。

在基于压缩感知的图像重构系统中，首先利用PDCT 得到观测值y，然后利用GPSR算法得到式（4）中的最优解ˆ。对于图像x，根据图像大小N 进行一维置乱后，再将其还原为2D图像，进行离散余弦变换（Discrete Cosine Transform，DCT），再从此系数中选择M 个元素作为观测值y，此时y=Φs（Φ 代表PDCT）。在实验中设定必要的参数：A=ΦΨ，AT=ΨTΦT，其中：Ψ 表示DT CWT，ΦT表示IPDCT，表示DT CWT 的反变换；根据GPSR 算法设定式（5）中的参数τ，以及迭代终止值δ；按照GPSR 算法的具体步骤完成变换系数的重构，得到αˆ；最后利用逆变换得到重构图像ˆ。

图1 2D DT CWT和2D DWT的方向小波及振幅变化Fig.1 Directional wavelet and amplitude variation of 2D DT CWT and 2D DWT

4 实验比较与分析

本文利用三幅大小为512×512 的灰度图像完成相关实验，如图2所示。

图2 实验灰度图像原图Fig.2 Original grayscale images used in experiments

首先比较不同小波基下，采用GPSR-Basic 和GPSR-BB 两种重构算法的差异。在实现过程中，τ=2.0，迭代终止条件为δ=10-3，小波基包括DT CWT 和JPEG2000 中使用的小波基CDF 9/7（双正交小波）。表1 给出了3 幅图像在不同采样率（M/N）下，利用不同小波基得到的峰值信噪比（Peak Signal-to-Noise Ratio，PSNR）。

表1 不同采样率下利用GPSR-Basic和GPSR-BB在DT CWT和CDF 9/7小波基下重构图像的PSNR对比 单位：dBTab.1 PSNR comparison of images reconstructed by GPSR-Basic and GPSR-BB based on DT CWT and CDF 9/7 with different sampling ratios unit：dB

由表1 可以看出，对于给定的采样率（0.1～0.5），利用GPSR-Basic 算法实现重构的图像的PSNR 值在多数情况下大于GPSR-BB 实现的图像的PSNR 值，但是差值小于1 dB，从视觉上不能直观分辨。在同一种重构算法下，采用DT CWT 小波基得到的重构结果均优于CDF。从PSNR 上来看，Lena 和Boat 图像差值在1.5 dB 左右，Barbara 图像的差值是2 dB 左右。图3是Lena图像在采样率M/N＝0.2时，在不同小波基表示下，利用GPSR-Basic 重构的结果及其局部放大图像，并将其与原始图像进行了比较。重构后的图像与原始图像相比，PSNR 在数值上相差1.72 dB，图3 中有肉眼可见的改善，由局部细节可以看出利用DT CWT 小波基重构的图像比较清晰，噪点明显减少。从表1中的PSNR数值来看，Lena和Boat图像差值在1.5 dB 左右，Barbara 图像的差值是2 dB 左右。由图2的原始图中可以看出，Barbara 图像中含有较多的纹理区域，对小波的方向性要求较高，最终的实验结果也表明DT CWT小波基在方向选择性和细节上优于CDF 9/7小波基。

图3 原始图像与DT CWT、CDF 9/7重构图像的比较(M/N=0.2)Fig.3 Comparison of original image and images reconstructed by DTCWT and CDF 9/7（M/N=0.2）

本文在选择DT CWT 小波基的基础上，将GSPR 算法与迭代阈值收缩（Iteration Shrinkage Threshold，IST）方法进行了比较，图4 是对Lena 图像利用三种方法实现重构时目标函数随时间的变化情况。随机投影部分选择的是PDCT，目标函数中的参数τ=2.0，迭代终止条件为δ=10-3，采样率为0.2。从运行时间和收敛情况上看，初始阶段IST的下降速度比GPSRBasic 略快，但是后续收敛变慢，达到终止的用时最久；GPSRBB的收敛速度最快，达到终止条件用时最少。

图4 不同重构算法下目标函数的变化Fig.4 Changes of objective function with different reconstruction algorithms

利用结构随机矩阵（Structurally Random Matrices，SRM）［18］对信号x 的处理过程可定义为y＝D ⋅F ⋅P（x），其中：P 表示对原始信号进行随机投影，可以随机置乱信号次序或者将信号符号随机置乱；F 表示正交变换矩阵，可选择快速傅里叶变换、离散余弦变换或沃尔什哈达玛变换，为了与前文的PDCT 相比较，本文选择的是DCT；D 表示根据采样率随机抽取数据，最终得到观测值y。

表2 给出了SRM 和PDCT 两种不同观测矩阵，在CDF9/7和DT CWT 两种小波基下，利用GPSR-BB 对Lena 图像重构结果的PSNR。由表2 可以看出，在CDF 9/7 和DT CWT 小波基下，利用PDCT 的结果均优于SRM；同一种随机观测矩阵下，DT CWT的结果优于CDF 9/7。

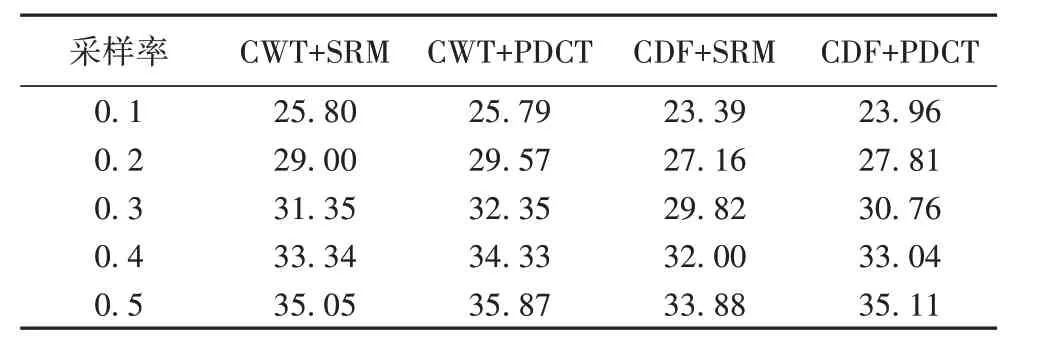
表2 不同随机投影方式的重构结果的PSNR 单位：dBTab.2 PSNR of reconstructed results of different random projection methods unit：dB

5 结语

本文利用图像在DT CWT 小波域的稀疏性，通过GPSR 算法实现了图像重构。实验在同一重构方法前提下比较了不同的稀疏表示域的PSNR 值，结果表明2D DT CWT 相比双正交小波（CDF 9/7）在重构细节上具有一定的优势，特别是在纹理较多的图像上优势明显；PDCT 的随机投影方式较SRM 也有提升；并且GPSR 的两种重构算法与IST 相比在收敛速度上提升明显。虽然DT CWT 在重构结果上有明显的提升，但由于其方向小波数量较多，重构的速度较之CDF 9/7 有所降低。对图像的稀疏表示仍在进一步研究中，可以考虑将其应用到模式表示的其他领域。