基于格子Boltzmann方法和大涡模拟的颈动脉分叉狭窄流动并行计算

张毅卓，葛 森，王良军，谢 江，曹 洁，张 武，*

（1.上海大学上海市应用数学与力学研究所，上海200444；2.上海大学计算机工程与科学学院，上海200444；3.上海交通大学附属仁济医院老年科，上海310101）

0 引言

颈动脉狭窄是颈动脉疾病的重要病因之一，常见的病变包括动脉粥样硬化、颈动脉斑块等，斑块的破裂导致缺血性脑卒中的产生［1-2］。随着病变区域的发展，颈动脉血管变得狭窄，从而阻碍血液流动，使得颈动脉血管内部的血流动力学发生复杂变化。

血管的壁面剪切应力（Wall Shear Stress，WSS）被认为是病变发生和发展的一个重要因素，并被广泛研究［3］。血流动力学的异常变化将会导致斑块和狭窄部位区域产生异常的WSS。较低的WSS是颈动脉粥样硬化病变早期发展的主要因素之一，剪切力的作用导致血管壁受到损伤，血小板的活性被激活，在斑块壁面出现局部聚集，引起颈动脉的进一步狭窄［4］。严重狭窄部位的斑块肩部会产生高WSS，使斑块可能出现裂缝、破裂和脱落，造成严重后果。

在传统的有限元和有限体积计算方法中，为了根据特定患者的临床数据计算WSS，首先基于超声获得患者的血流速度，将利用核磁共振成像（Magnetic Resonance Imaging，MRI）获得的患者颈动脉血管几何形状转换为标准有限元/有限体积求解器所需的三维网格［5］，并导入求解器进行求解，计算速度场并在血管壁面进行梯度计算。这种方法存在的问题是模型网格生成的预处理和求解器计算时间过长，限制了其在实际患者诊断中的适用性。

颈动脉处的血液流动是复杂的牛顿粘性流体运动，一般可以通过N-S（Navier-Stokes）方程来进行描述。格子Boltzmann 方法（Lattice Boltzmann Method，LBM）是一种针对流动问题求解的有效方法［6］。基于Boltzmann 方程，它的物理基础主要包括两部分：一是在介观层面考虑粒子运动和对粒子之间的迁移、碰撞进行近似与简化；二是通过时间、空间和粒子迁移方向的离散，使用离散速度模型来模拟流体运动。LBM 通过Boltzmann方程描述粒子分布函数随时间的演化，通过粒子分布函数的求和可以得到流体的速度、密度和压力等宏观量。通过对时间、空间和粒子迁移方向的离散化，LBM具有天然的可并行性、容易编程和高精度等优点，能够在并行计算机上进行有效计算，非常适合处理复杂几何形状和复杂流动的大规模计算问题［7］。

LBM在颈动脉数值模拟领域已有初步的研究。利用多松弛时间格子Boltzmann（Multi-Relaxation-Time Lattice Boltzmann，MRT-LB）方法模拟了三维狭窄和正常颈动脉分叉的脉动流模式［8］。对血液的牛顿模型和非牛顿模型应用LBM，并在稳态流动和脉动流动的背景下进行了研究。分析了WSS 对动脉粥样硬化的影响，证明LBM 适用于研究动脉粥样硬化发展引起变化的流体［9］。给出了LB 模型中三维WSS计算的公式，采用改进的算法，计算了人体腹主动脉壁剪切应力等［10］。

上述研究都是在较低雷诺数（Re=500～600）下进行的。考虑到血液是一种典型的脉动流动，动脉处的狭窄大大增加了产生复杂流动的可能性，包括考虑对应更高Re的流动。复杂流动会对狭窄部位下游区域的压降和WSS 产生显著影响，两者都会对颈动脉壁面产生实质性的负面影响。从精确计算的角度来看，采用经典LBM 模拟这种流动面临较大的挑战［11］。

大涡模拟（Large Eddy Simulation，LES）方法已被证明对复杂流动具有较强的数值模拟能力［12］。在LES 中，用非稳态的Navier-Stokes 方程来直接模拟大尺度涡，而较小尺度的涡对大涡的影响则通过近似模型来模拟，采用的模拟方法称为亚网格尺度（SubGrid Scale，SGS）模型［11，13］。

LES 有许多优点，在SGS 模型的帮助下，空间和时间分辨率可以进一步增加。LES 提供了关于流动的大涡的精确信息，能够提供更好的物理洞察力，并有潜力成为更准确的预测工具［14］。通过LES 计算主动脉内的扰动流场和壁面剪切应力，使用磁共振成像（MRI）的临床数据作为输入的模型，可以很容易地找到主动脉壁上较高WSS 的位置［15］。Vergara 等［16］通过研究腹主动脉瘤向湍流的过渡，把临床和计算结果加以对比，表明LES模型具有较好的适用性。因此，在颈动脉狭窄流动数值模拟中考虑大涡模拟，将LBM 与LES 相结合，充分利用LBM 的并行特性和LES 对复杂流动的精确描述，以减少计算时间，提高计算精度，有利于更好地理解颈动脉狭窄后部的血液流动，可能会对临床上提供更准确的诊断指导。

LBM的计算时间通常随着网格尺度的减小和雷诺数的增加而增加。但随着多核处理器的快速发展，在大规模并行架构上采用OpenMP 并行编程模型能够显著减少程序求解的运行时间，提高模拟速度［17-18］。

本文的主要工作是提出了LBM 结合LES 的并行算法——LBM-LES颈动脉模拟算法来对颈动脉狭窄部位的脉动流动进行数值模拟；并针对计算时间较长的挑战，采取OpenMP模型对该算法进行并行加速［19］。血管几何模型由MRI临床数据建模得到，颈动脉脉动血流不同时刻的速度则由B 超检查得到，根据实测参数和几何模型，通过LBM-LES 并行算法模拟出不同脉动时刻的三维颈动脉的血流速度和WSS。最后分析了实验结果，评估了不同核数下的计算时间和加速比。

1 格子Boltzmann方法

LBM 源于格子气自动机，通过Boltzmann 方程，对时间和空间进行离散化，用离散的模型从介观上模拟复杂的流动现象。LBM 的离散模型通常定义为DmQn，下标表示m 维空间和格子上n个离散速度方向。

LBM 在相空间将粒子的速度u 简化为有限维的速度空间{e0，e1，…，en-1}，引入了n 个分布函数fi(x，t)(i=0，1，…，n-1)来描述离散时间步长t 下沿ei方向流动的粒子。经典的LBGK（Lattice Bhatnagar-Gross-Krook）演化方程［6，20］具有以下形式：

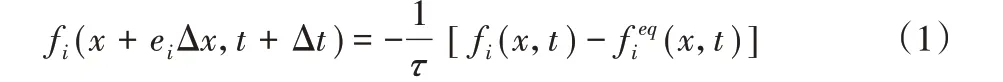
其中：Rg为流体常数，T 为流体温度。无量纲松弛时间τ 与声速cs和流体的运动粘度ν 有关，可以用表示。格子单位Δx、时间步长Δt和流体密度ρ 的单位分别为m、s 和kg/m3。

以D3Q19格子模型为例来说明LBM。如图1所示，图中0，1，…，18 对应表示e0，e1，…，e18，其中e0位置是流体粒子的初始位置，e1，e2，…，e18指定粒子在碰撞后流向的方向。

三维模型下所设的微观速度为：

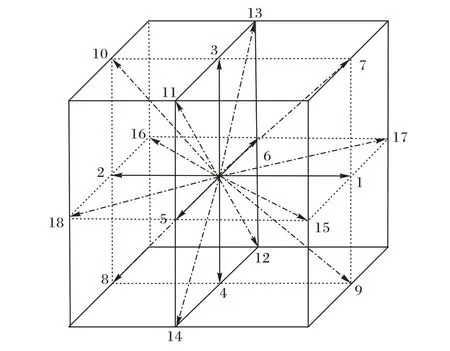
图1 D3Q19离散速度模型Fig.1 D3Q19 discrete velocity model

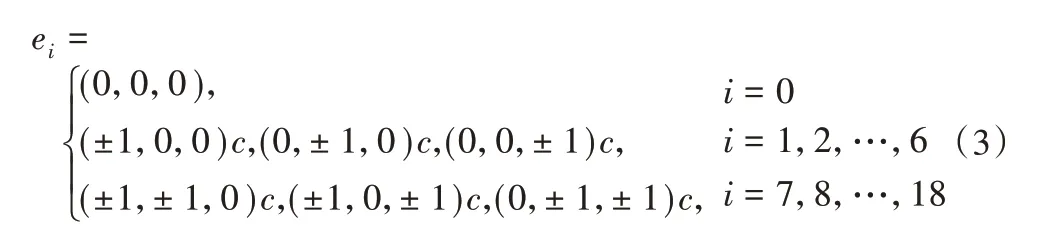
根据LBGK方程，LBM的演化可分为以下两个步骤：

1）碰撞。

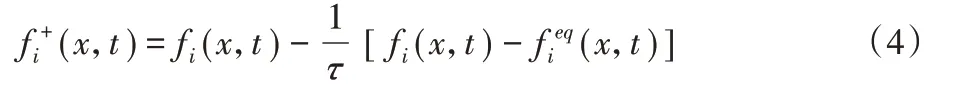
2）迁移。

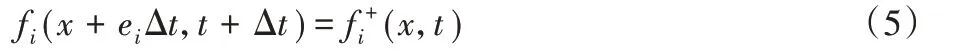
在格子单元中，时间步长和空间步长通常相同，因此c=Δx/Δt=1。格子声速取值，当速度较低时，局部平衡态分布函数可以采用Maxwell 分布的二阶Taylor 展式，模型的分布函数如下：

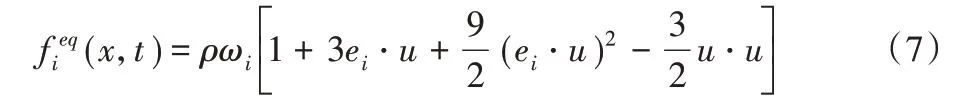
相应的权重系数为：

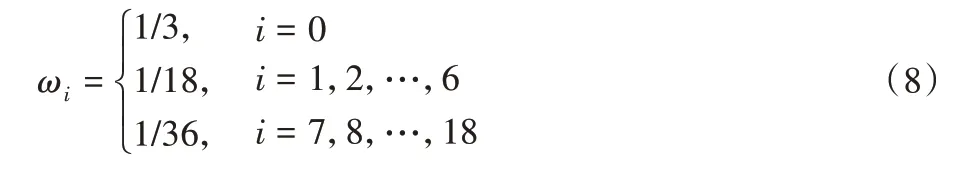
2 壁面剪切力的数值解

血液在血管中流动时，会对血管壁表面施加作用力，壁面剪切应力表示血液对血管壁面单位面积上所施加的剪切力。对于颈动脉粥样硬化和斑块部位，血管被设定为刚性壁面，血流可以被精确地建模为均匀介质、不可压缩的牛顿流体，对于直径较大的血管，如颈动脉，这通常被认为是可接受的［9］。

当物体在血管壁面流动时，壁面速度变为零，无滑移边界条件成立。对于不可压缩的牛顿流体，还需要血管壁面的三维空间信息和血管内血流速度，以及相应的壁面法向量［3］。WSS可以通过剪切力张量σ和边界法向单位矢量n确定：

D3Q19模型的壁面剪切应力计算公式［10］如下：

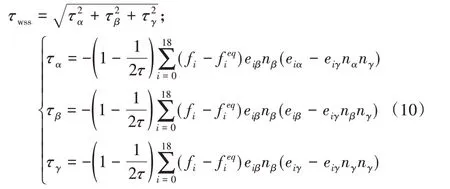
其中，α，β，γ代表三维空间内不同的维度。

3 LBM-LES并行算法

3.1 大涡模拟

大涡模拟的精度很高，能够模拟瞬时流场运动。考虑到脉动血流的影响，同时为了精确描述流体运动，本文采用大涡模拟结合LBGK模型来对颈动脉狭窄流动进行数值模拟。

LES 的基本思想是采用滤波器控制方程进行滤波，从而把复杂的流动现象分解为大尺度结构和小尺度结构。在数值模拟时对大尺度的流动现象进行直接模拟，针对小尺度脉动采用SGS模型进行模拟，模型的网格尺度可以设为大尺度，在格子内采用SGS模型来进行更小尺度的模拟。在采用适当的亚格子模型的情况下，这样能够模拟真实物理情况下的瞬时流场。

在LBGK 模型中加入LES 的SGS 模型，采用经典的Smagorinsky 模型［11-12，21］。在LBM-LES 方法中，Smagorinsky 模型的引入是通过改变原有LBM 碰撞模型中的无量纲松弛时间τ来实现的。

引入LES后的有效粘性可以表示为：

其中：v0是层流粘性，vt是涡粘性。由Smagorinsky 模型给出涡粘性即为SGS模型。

在Smagorinsky模型中，涡粘性vt由应变率张量

和滤波尺度Δ确定，如式（13）所示：

其中：Cs是Smagorinsky 参数，|S|为应变率张量Sαβ的模。|S|在LBM模型中可以通过下式获得：

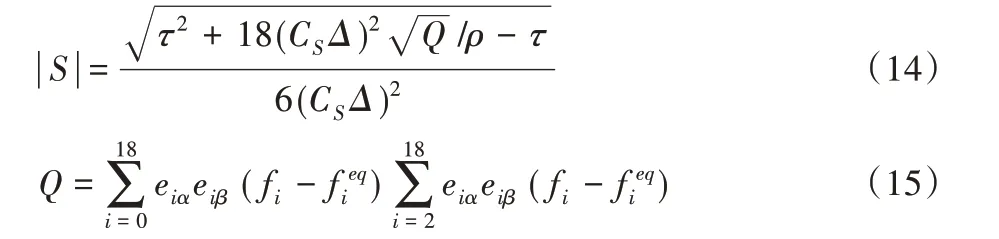
3.2 并行算法实现

LBM-LES 并行算法具有LBM 的可并行化优点，可以采用OpenMP 模型进行加速。本文采用的OpenMP 是用于共享内存机器的一套并行编程库。程序在运行时采用fork/join 的并行模式。首先主程序执行串行代码，在执行到包含#parallel 编译指令的代码段时，主进程派生出子线程分配给多处理器的不同计算核来处理计算任务，实现线程级别的并行计算，子线程执行完毕后销毁，继续执行主进程的任务。

为了更好地描述LBM-LES 并行算法，给定程序输入为：网格模型和计算参数；程序的输出为：网格格点数据文件，包括格点坐标、流速分量、剪切力分量和压力信息。

本文所采取的LBM-LES并行算法的具体计算步骤如下：

步骤1 设定好颈动脉计算区域和最小网格尺寸，读入面网格文件；

步骤2 判断血管边界，遍历标记计算网格；

步骤3 读入数值计算参数，包括速度向量、雷诺数、特征长度和迭代步数等；

步骤4 遍历网格点，进行计算数据初始化；

步骤5 在LBGK模型碰撞过程中计算Smagorinsky参数，引入LES；

步骤6 模型迁移过程；

步骤7 宏观量计算过程，得到宏观速度、压力、剪切力、以及对应速度三维分量、剪切力三维分量；

步骤8 若满足设置的输出迭代步数条件，输出中间计算结果；

步骤9 判断是否收敛，若不满足收敛条件，重复步骤5～7，否则结束，输出程序计算信息，终止计算。

根据LBM-LES 模型和OpenMP 编程模型给出整体的并行算法，如图2 所示。首先，程序读入光固化立体造型术（STereoLithography，STL）网格文件，在网格的初始化过程中，由于每个格子的不相关性，每个格子类型的判断以及格点上微观量的初始化都可以进行并行操作，加快处理速度。在迭代过程中，网格的碰撞和迁移过程都可以采用合适的OpenMP指令来实现。同时，宏观量的计算只和格子自身存储数据有关，因此也可以采用并行算法来进行加速。直到最后满足程序终止条件，输出迭代结果。

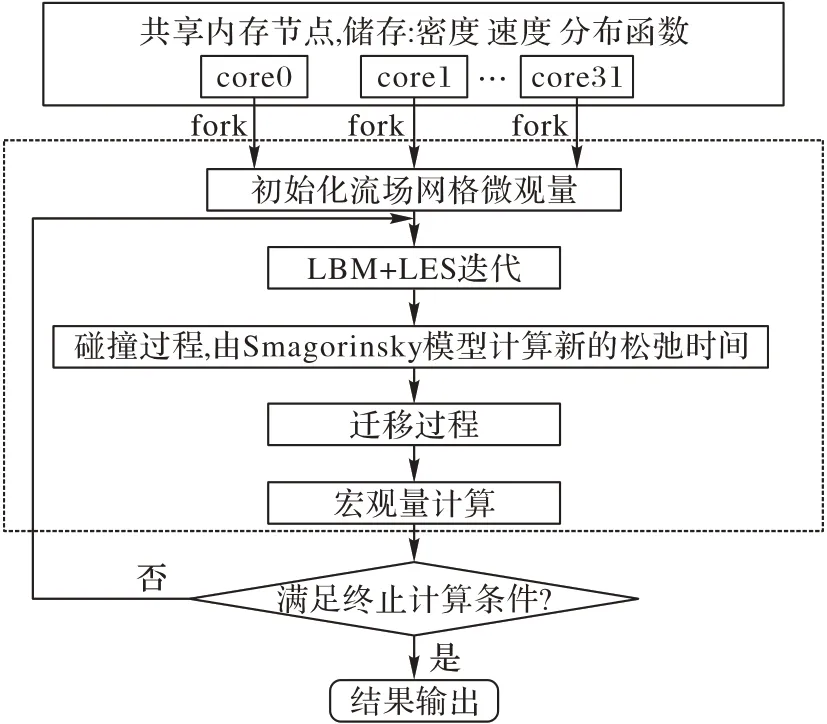
图2 本文并行算法流程Fig.2 Flowchart of the proposed parallel algorithm

4 数值实验与分析

4.1 实验环境

实验在上海大学高性能计算集群“自强4000”上进行并行性能测试，所用共享内存节点具体配置信息如下：4 颗Intel Sandy Bridge 架构的E5-4650 CPU（2.7 GHz/8-core），512 GB RDIMM DDR3 1 600 MHz 共享内存，计算队列共计32 个计算核数，编译命令采用“-O3”选项进行优化。

4.2 计算模型

程序读入的网格文件为真实颈动脉血管模型，通过从合作医院临床采集得到的MRI 图像数据，应用医学后处理软件MimiCS 软件进行三维重构，采用阈值分割的方法分离血管周围组织，从而得到颈动脉血管真实几何模型［22］，并导出为STL格式的网格文件。颈动脉三维几何模型如图3 所示，血流方向从下至上，血流从颈总动脉（Common Carotid Artery，CCA）入口流入，从颈外动脉（Externl Carotid Artery，ECA）、颈内动脉（Internal Carotid Artery，ICA）流出。计算区域的高度为CCA入口和ECA、ICA出口之间70.0 mm的区域。

由于计算的真实血管形状非常复杂，要精确描述血管壁面区域的不规则形状，需要在适当的位置采用阶梯逼近或者插值处理，以保证满足物理边界上的条件。因此，边界条件采用YMS 曲线插值处理［23］，在每次碰撞迁移的过程中，需要在每个与物理边界相交的网格线上进行插值处理，血管壁面均采用无滑移边界条件。

为了模拟脉动流动，在一个脉动周期内，在不同的时间点来改变CCA 入口的血流速度，分别模拟最小舒张速度（Velocity Minimum，VM）、最 大 收 缩 期 速 度（Velocity Maximum，VMAX）、双侧切速度（Velocity in Dicrotic Notch，VDN）和舒张流动后期速度（Velocity in Diastolic Flow pHase，VDFH）。在具体计算过程中，分别在参数初始化（迭代步数为0），迭代步数为800、1 200、1 600 的时刻改变颈动脉入口的流速，来模拟脉动流动的情况。表1 给出了三维算例不同时间点的具体计算数据。

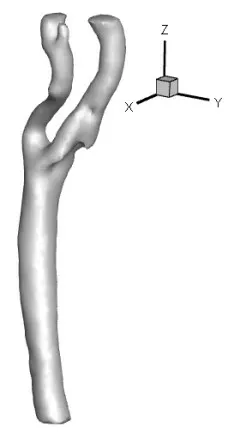
图3 三维血管模型Fig.3 Three-dimensional carotid model

表1 脉动血流参数Tab.1 Pulsating blood flow parameter

4.3 数值实验

通过对不同雷诺数下的颈动脉狭窄流动计算，图4、5 分别给出了雷诺数为500（LBGK模型）、2 000（LBM-LES模型）情况下在不同时刻（迭代步数800、1 200、1 600、2 000）的流速云图和剪切力矢量图。

4.3.1 流速矢量图

如图4 所示，图（a）～（d）分别代表四个不同时刻的颈动脉分叉部位X轴方向的截面图。对于存在斑块区域的狭窄颈动脉血管模型，血流在流过弯曲部位导致血流形态发生变化，在ICA 处具有较大的血流速度，同时斑块后段产生一个小的血流较低的区域，这种流动情况会导致斑块的继续生长，病变区域继续向下游扩展，随着斑块进一步进行扩大，颈动脉的狭窄变得更加严重。当Re=2 000 时，结合LES，在不同时刻的截面中，血液流动变得复杂，在收缩期间，斑块附近的流动区域具有较大的流速，在狭窄段的下游区域，血流流过狭窄区域之后流速上升。

4.3.2 剪切力矢量图

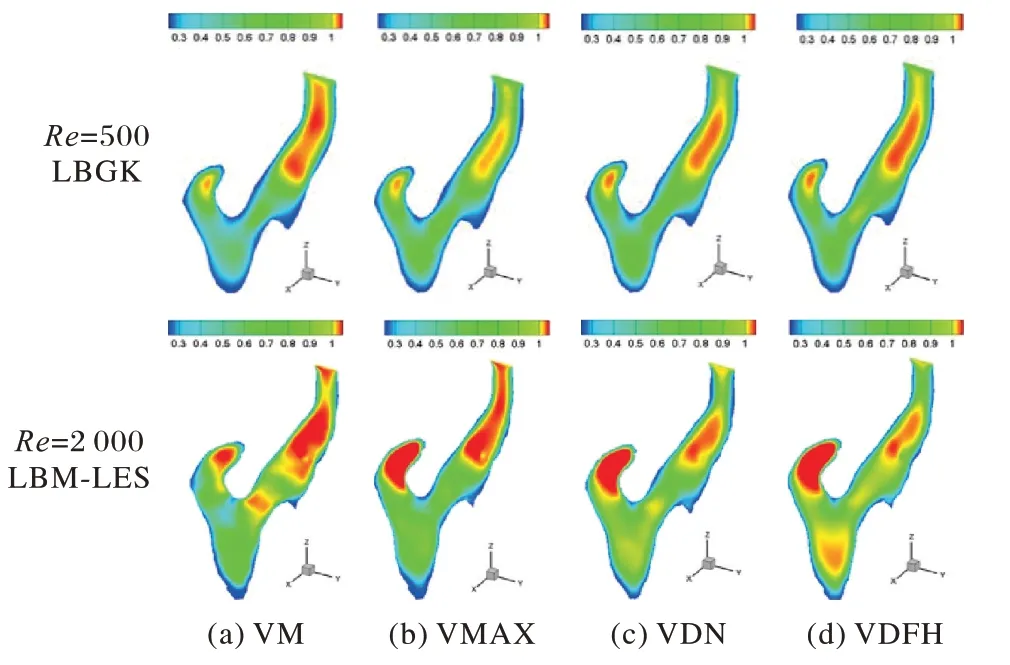
图4 流速云图Fig.4 Velocity cloud chart

本小节对血管WSS 进行分析。如图5 所示，根据壁面剪切力的矢量云图可以很明显看出：在收缩期之前，斑块处WSS较小（图（a）），随着收缩期，血流速度升高，斑块肩部产生较大的WSS（图（b）），在狭窄段的下游区域两侧，具有高WSS；随着收缩期结束，斑块处WSS 开始减小，在刚开始进入舒张流动后期，斑块处WSS 较高。而在较高雷诺数的情况下，同样参数条件的WSS 比低雷诺数情况下要高，在斑块肩部产生高WSS，在斑块尾部产生一个WSS 尖点，高WSS 会导致血管壁面的损伤，进而促进斑块的扩张。

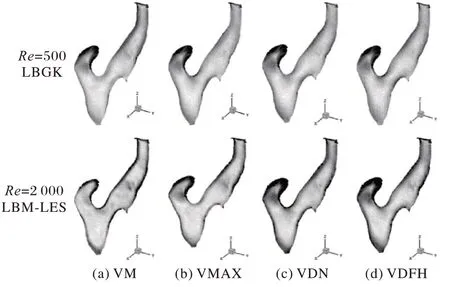
图5 剪切力矢量图Fig.5 WSS vector diagram

4.3.3 并行时间和加速比

本文计算程序在高性能集群共享内存节点上进行并行性能的测试。在提交任务队列时设置运行参数，分别采用4 个、8个、16个、24个和32个核来迭代计算2 000步，计算网格量固定，数值实验算例的网格总数固定为4 000 万，所得运行时间数据为三次计算结果的平均值，包括网格生成、初始化、碰撞迁移和宏观量计算过程。计算时间并未考虑计算结果的输出时间。图6给出了不同计算核数下程序的运行时间，图7给出了不同计算核数的程序加速比。

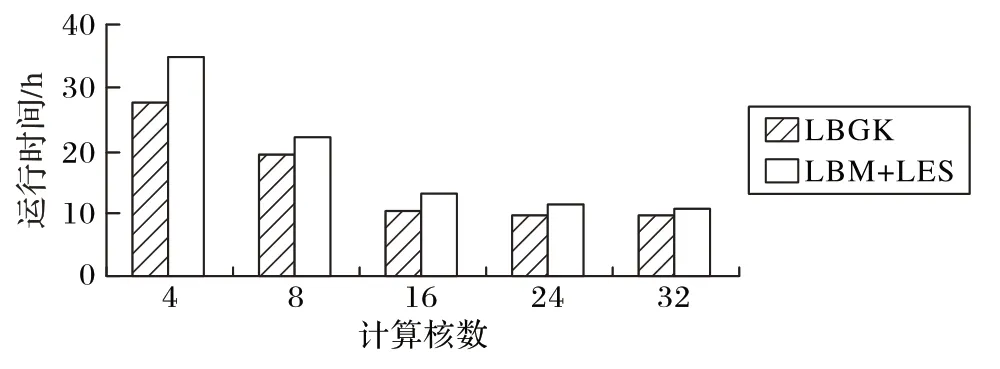
图6 LBM和LBM-LES模型在不同核数下的运行时间对比Fig.6 Running time comparison of LBM and LBM-LES models with different cores

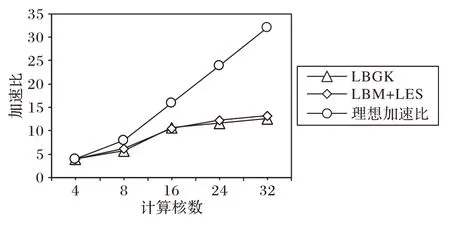
图7 LBM和LBM-LES模型在不同核数下的加速比对比Fig.7 Speedup comparison of LBM and LBM-LES models with different cores

从图6 可以看出，LBM-LES 的计算时间要略高于原有LBM 模型，这是由于额外计算松弛因子所增加的计算开销。随着计算核心数量的增加，程序的运行时间逐渐减少。从图7 可以看出，加速比的增长率在计算核数4～8，8～16，16～32 的阶段呈现出先上升后下降的趋势，随着核数的增加，性能增益相对降低，两个不同模型之间的加速比相对较符合。这很可能是由于集群共享内存节点一块E5-4650 CPU具有8个核心，不同CPU 之间的计算核之间数据通信会对程序的加速效果产生影响，数据的传递和通信是耗时的，结果低于理想加速比。同时，随着计算网格量的增加，OpenMP 并行编程模型的并行性能逐步降低，采用MPI进行跨节点的并行加速，将会进一步提高并行性能。

并行计算实验结果显示了在高性能集群上采用并行加速算法能够有效缩短LBM-LES 算法的计算时间，如何充分发挥大型超级计算机的并行计算能力，进行跨节点MPI 编程模式的大规模问题的LBM-LES 并行计算，深入开展颈动脉狭窄血液流动精确计算，是今后进一步的研究内容。

5 结语

本文介绍了LBM 结合大涡模拟模型在模拟动脉狭窄血液流动研究中的应用，验证了大涡模拟模型适合于颈动脉复杂脉动流动的模拟和分析，然后对模拟的程序进行了优化与并行。

针对临床数据，采用三维模型重构方法构建颈动脉模型，基于LBM-LES 模型，计算了得到的三维真实血管，在一个脉动周期内，给出了特征时间点的速度云图、WSS矢量云图的瞬时分布，模拟的流动在不同位置显示出许多特征，这些信息对于理解复杂的动脉血流和诊断动脉疾病方面可能是非常有帮助的。利用OpenMP 编程模型对程序进行并行加速，明显地缩短了程序计算时间，并实现了较好的加速比。

通过快速计算实际脉动流动的复杂状况，为个体颈动脉内进行体外非侵入式仿真模拟血流动力学分析提供了一种可行的方法，通过并行加速能够在较短时间为医生诊断颈动脉斑块疾病提供一定的理论依据和辅助作用，为颈动脉斑块体外辅助诊治提供帮助。