使用深度对抗子空间聚类实现高光谱波段选择
曾 梦,宁 彬,蔡之华,谷 琼
(1.湖北文理学院计算机工程学院,湖北襄阳441053;2.中国地质大学(武汉)计算机学院,武汉430074)
0 引言
高光谱图像(HyperSpectral Image,HSI)由上百个光谱波段组成,包含丰富的空间信息和光谱信息,通常利用分类技术实现具有细微光谱差异地物的区分。目前,高光谱图像分类已经被广泛用于军事目标识别[1]、海洋环境监测[2]和城市管理[3]等多个方面。然而,由于高光谱图像光谱波段之间相关性强且具有较高的冗余度,导致分类复杂性高、“维度灾难”等[4]问题的发生。高光谱波段选择旨在选取原始波段集中较为重要的波段子集来降低数据的维度,从而降低原始数据的计算量并保证分类具有较高精度[5]。
近些年,国内外学者提出了很多波段选择方法,大致可以分为三类:基于排序策略、基于搜索策略和基于聚类策略。基于排序策略的方法通过评估每个波段的重要性来分配权重进行排序,例如最大方差主成分分析(Maximum Variance Principal Component Analysis,MVPCA)[6]、拉 普 拉 斯 评 分(Laplacian score,Lap-score)[7]以及基于稀疏表示的波段选择(Sparsity-based Band Selection,SpaBS)[8]等。基于搜索策略的方法使用启发式搜索算法优化给定的度量,如演化多目标优化(evolutionary multiobjective optimization)算法[9]等,但是基于搜索的方法通常耗时较多。基于聚类的方法假设波段根据它们的相关性可分离,通过聚类结果进行波段选择,例如改进的稀疏子空间聚类算法(Improved Sparse Subspace Clustering,ISSC)[10]、稀 疏 非 负 矩 阵 分 解(Sparse Nonnegative Matrix Factorization,SNMF)[11]等。由于基于聚类的方法充分考虑了波段之间的相关性,能够得到较好的波段选择结果,因此得到了越来越多的关注。
上述基于聚类的算法虽然能得到较好的结果,但是很多基于聚类的方法忽略了光谱波段之间的相关性。子空间聚类算法是广泛应用的聚类算法,但很多子空间聚类算法仅对于线性子空间进行聚类,这不适用于具有非线性关系的高光谱图像的波段选择。最近提出的一种深度子空间聚类(Deep Subspace Clustering,DSC)[12]网络将深度卷积自编码器和子空间聚类相结合,使用该算法进行波段选择[13]很好地解决了上述问题并取得了较好的效果;然而,DSC算法仍然将自表达作为监督,对于某些内在子空间不独立或具有明显交集的样本可能表现不佳。
本文利用深度对抗子空间聚类(Deep Adversarial Subspace Clustering,DASC)[14]网络进行高光谱波段选择。DASC网络是一种新的无监督深度子空间聚类模型,该网络在DSC 网络的基础上加以改进,将DSC 和生成对抗网络(Generative Adversarial Network,GAN)[15]相结合,引入对抗学习来监督自编码器的样本表示和子空间聚类,使得子空间聚类具有更好的自表达性能。此外,引入拉普拉斯正则化来考虑反映图像几何信息的局部流形结构,使网络性能更优。
1 相关工作
1.1 子空间聚类
对于一个原始数据集X=[x1,x2,…,xN]∈ℝd×N,假设该数据集属于n 个线性子空间S=S1,S2,…,Sn,线性子空间的维度分别为d1,d2,…,dn,有如下公式:

s.t.X=XC,diag(C)=0
其中:C ∈ℝN×N表示自表达系数矩阵,diag(C)=0 为了避免平凡解,‖ ∙ ‖p可以表示为l1或l2正则化。对于稀疏子空间聚类(Sparse Subspace Clustering,SSC)[16],通常有如下公式:

s.t.di ag( C )=0
其中,λ 表示平衡系数。使用系数矩阵C 构造相似矩阵M=|C|+|C|T,通常情况下,相似矩阵M 为块对角矩阵。将矩阵M用于谱聚类进行聚类,得到最终的聚类结果。
1.2 卷积自编码器
卷积自编码器(Convolutional AutoEncoder,CAE)[17]由一个对称的编码器和解码器组成,编码器和解码器都由卷积神经网络构成,用φ=E(X;αe)表示编码器,其中:X 表示输入,αe表示参数,φ 表示编码器的输出。对于解码器,采用和编码器相同的结构,不同的是解码器操作用于重建输入的X 表示为最后,使用均方误差作为损失函数进行训练,损失函数如下:

1.3 深度子空间聚类
深度子空间聚类(Deep Subspace Clustering,DSC)网络将自表达层嵌入在卷积自编码器中,输入数据X 经过编码器得到特征表示,U然后经过自表达使用UC进行全连接,再将UC经过解码器得到重构的DSC的损失函数L如下:
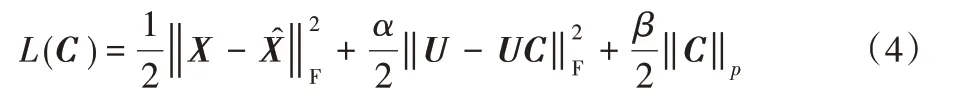
s.t.diag(C)=0
2 深度对抗子空间聚类实现波段选择
2.1 深度对抗子空间聚类
深度对抗子空间聚类(DASC)网络由子空间生成器和判别器两部分组成:在生成器中,使用一个卷积自编码器来学习样本表示,自表达层嵌入在编码器和解码器中用来得到样本的相似矩阵并使用Ncut 方法进行聚类,然后以聚类生成的簇为条件生成“真样本”和“假样本”;对于判别器,接收生成的真假样本,并且区分出真样本和假样本。通过DASC 网络训练,最终得到系数矩阵C,通过谱聚类得到聚类结果。
2.1.1 生成器
对于真样本的获取,通过自表达层学习的相似矩阵运用Ncut 算 法 得 到k 个 簇A={A1,A2,…,Ak}及 特 征 表 示Z=[Z1,Z2,…,Zk],然后计算每一类Ai中每个样本到相对应的子空间Si的投影残差,投影残差的求解在判别器中执行,然后选择具有较小残差的mi个数据作为真样本。投影残差的公式如下:

其中,Vi表示投影矩阵。由此生成器的对抗性损失为:

对于假样本的获取,在每个簇Ai中,采样层从估计的子空间Si中进行随机采样,假设簇Ai具有mi个样本,采样层从(0,1]均匀分布中随机采样mi个随机向量,然后将αt的每一项和簇Ai中对应样本相乘并求和,生成mi个假数Zˉt=,其中θtj表示θt的第j项。
为了使生成的假数据更接近判别器学习的子空间,使聚类具有更好的效果,将对抗损失加入到生成器的损失函数中,公式如下:
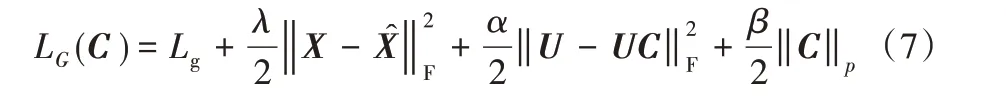
s.t.diag(C)=0
其中,λ 表示平衡系数。式(7)右边的四项分别表示对抗性损失、重构损失、自表达损失和自表达系数损失。
2.1.2 判别器
在判别器中,通过投影残差Lr来区分真样本和假样本,通常来说,若簇不准确则真样本将比假样本更接近子空间。对于簇Ai的训练,使用映射残差定义一个样本属于子空间的概率,损失函数如下:
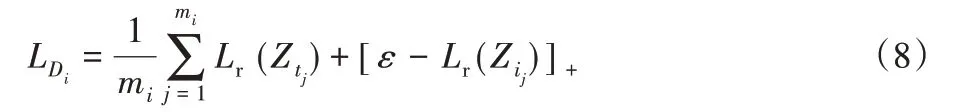
其中:[∙]+=max(0,∙)为附加的边缘损失,ε 为正边缘参数。对于k个簇来说,判别器的损失函数为:


2.2 拉普拉斯正则化DASC
为了更好地利用图像的局部流形结构信息,在生成器的损失函数中加入拉普拉斯正则项[18]。将n 个样本作为n 个顶点X=[x1,x2,…,xN]用边连接起来构成图,其中xi∈ℝd。定义W ∈ℝn×n作为权重矩阵来记录每条边的权重,则顶点i 和j之间的权重可以表示为:
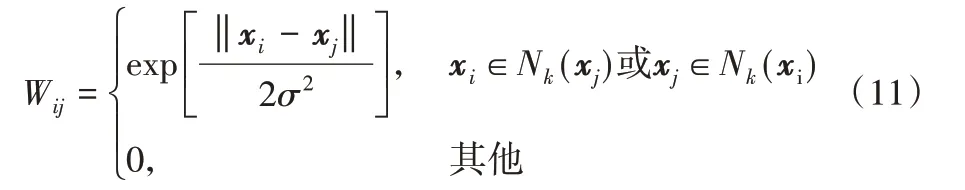
其中:Nk表示具有n 个顶点的K 最近邻(K Nearest Neighbors,KNN)的构造,σ是热核参数。
对于非线性流形结构,可以通过线性子空间局部近似,因此定义二次能量函数Q来计算两点之间的相似性:

其中q(x)=xTw+b为线性表示。
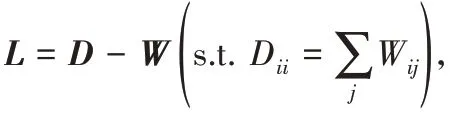

综上所述,最终得到生成器的损失函数为:
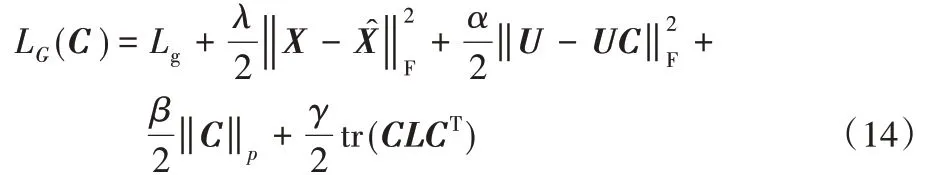
s.t.diag(C)=0
其中:tr(⋅)表示矩阵的迹,γ是平衡系数。
2.3 拉普拉斯正则化DASC实现波段选择的流程
利用深度对抗子空间聚类得到最终聚类结果,根据聚类结果求出每一类中波段的平均值作为聚类中心,然后计算每个波段到该类聚类中心的距离,选出每个类中最接近聚类中心的波段得到波段子集,即为波段选择的结果,具体流程如下:
1)输入三维高光谱数据集X,设置波段选择数量k。
2)构建DASC网络,初始化网络参数。
3)使用深度子空间聚类(DSC)网络对数据进行训练得到自表达系数矩阵和特征表示。
4)使用自表达层得到的数据,采用Ncut 方法进行聚类,得到“真样本”,并根据聚类个数生成m个假样本;并判断生成器训练是否大于5 次,如果是则进行下一步,否则返回到步骤3)。
5)根据生成器生成的真假样本,对判别器进行训练。判断如果总迭代次数大于300,则进行下一步,否则返回到步骤3)。
6)将DASC 网络训练得到的系数矩阵C 用于谱聚类得到聚类结果,计算得到每个类的聚类中心,并计算每个类中离聚类中心最近的波段作为代表波段,得到波段子集,即为波段选择结果。
3 实验结果与分析
3.1 实验数据和预处理
Indian Pines 数据集使用AVRIS 传感器在美国印第安纳州西北部的一块小区域收集,包含145 像素×145 像素,预处理后波段数为200,主要地物为16类。为方便实验,选取像素区间在[50 ∼120,50 ∼120]的数据子集进行实验,共包含8类,如图1所示。

图1 Indian Pines 数据集Fig.1 Indian Pines dataset
Pavia Center数据集使用ROSIS传感器在意大利北部帕维亚大学收集,包含1 096 像素×715 像素,预处理后波段数为102 个,主要地物为9 类。为方便实验,选取像素区间在[100 ∼200,200 ∼400]的数据子集进行实验,共包含6 类,如图2所示。
图2 Pavia Center 数据集Fig.2 Pavia Center dataset
详细的数据总结在表1 中给出。所有方法均使用python 3.5进行实验评价,DASC算法采用tensorflow框架。

表1 Indian Pines和Pavia Center数据集参数设置Tab.1 Parameters setting of Indian Pines and Pavia Center datasets
3.2 实验结果对比
使用Indian Pines 数据集和Pavia Center 数据集设计实验验证DASC 算法进行波段选择的效果。实验使用支持向量机(Support Vector Machine,SVM)[19]分类器进行波段选择后的数据分类,采用总体精度(Overall Accuracy,OA)、卡帕系数(Kappa Coefficient)以及平均精度(Average Accuracy,AA)来评价分类效果。在实验中,设置波段数为5~40,间隔为5个波段。对于Indian Pines 数据集,设置式(14)中的λ=0.4,α=15,β=1,γ=10;对于Pavia Center 数据集,设置式(14)中的λ=0.2,α=20,β=1,γ=15。对于自编码器的通道数设置为10-50-100-C-100-50-10,卷积核大小为3×3×3。将DASC 和Lap-score、SpaBS、ISSC、SNMF、MVPCA、DSC 等6种方法进行比较,得到的实验结果如图3、图4 所示。从图中可以看出,采用DASC方法进行波段选择的效果明显比其他方法更优。DSC和ISSC方法的效果比SpaBS、SNMF、MVPCA方法好,特别是DSC 方法表现出较好的实验效果,这表明将深度学习和子空间聚类算法相结合,对高光谱图像波段选择具有很好的应用价值,而使用DASC 方法,解决了DSC 方法的不足,在OA、AA和Kappa系数的比较中都得到了比DSC更好的结果。
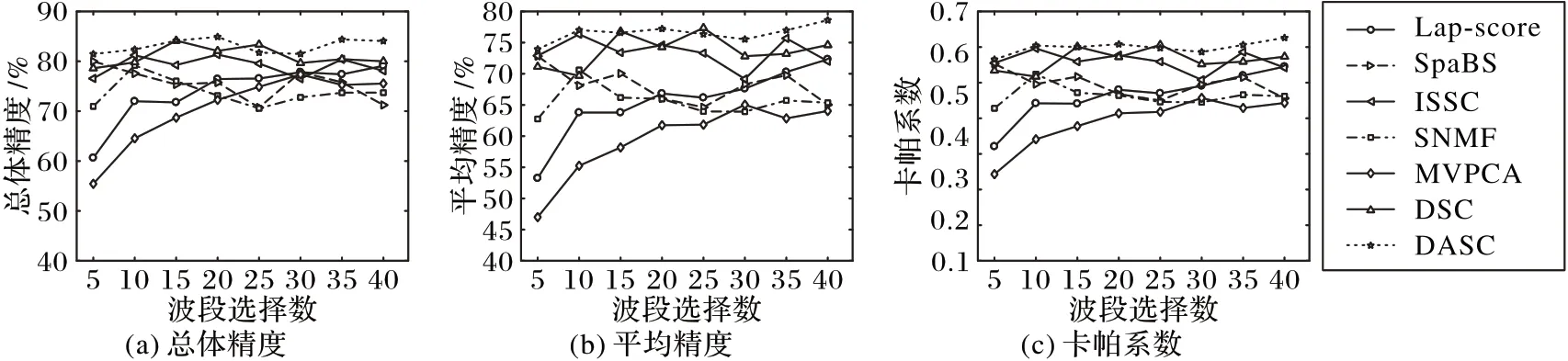
图3 Indian Pines数据集实验结果比较Fig.3 Experimental result comparison on Indian Pines dataset
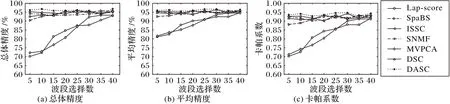
图4 Pavia Center数据集实验结果比较Fig.4 Experimental result comparison on Pavia Center dataset
3.3 波段选择分析
为了更好地分析波段选择的结果,使用Indian Pines 数据集,对波段选择数为20 时的波段号进行分析,分别得到不同方法选择20 个波段时的波段号。为了直观表示波段选择的结果,画出Indian Pines数据集200个波段的信息熵,信息熵越大表明该波段的信息量越多,波段更具有代表性。将选择的波段号在图中画出,如图5、图6所示。
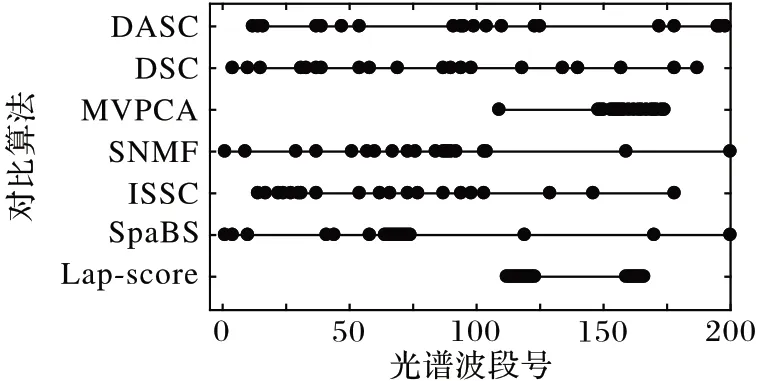
图5 选择波段数为20时不同方法的波段分布比较Fig.5 Comparison of band distribution of different methods when the number of bands is 20
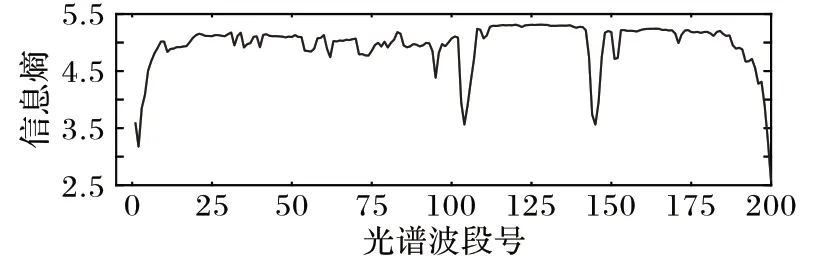
图6 选择波段数为20时光谱波段信息熵Fig.6 Spectral band information entropy when the number of bands is 20
从图6 中可以看出,信息熵的值比较平均,仅在某些地方呈下降趋势,因此选择波段分布较为均匀的方法更好。对应到图5 中,对于不同方法得到的波段选择结果有很大的差别,其中Lap-score 和MVPCA 方法得到的波段号较为集中,而且仅出现在某一区间内,波段之间具有很强的相关性;SpaBS、ISSC 和SNMF 方法选择的波段在前面较为集中,而后面比较分散,分布不均匀;DSC 和DASC 方法得到的波段号分布均匀,且选出的相邻波段较少,具有很好的代表性,因此能得到更好的分类效果。通过3.2 节的实验结果比较,可以证实DASC方法选出的波段比其他方法更优。
3.4 计算时间对比
该实验将DASC 方法和其他6 种方法在波段选择数量均为20 时的计算效率进行比较。不同方法在Indian Pines 和Pavia Center 数据集上的运行时间如表2所示。实验方法在配置为Inter Xeon E5-2620 CPU 2.10 GHz 和32 GB 内存的服务器上进行。
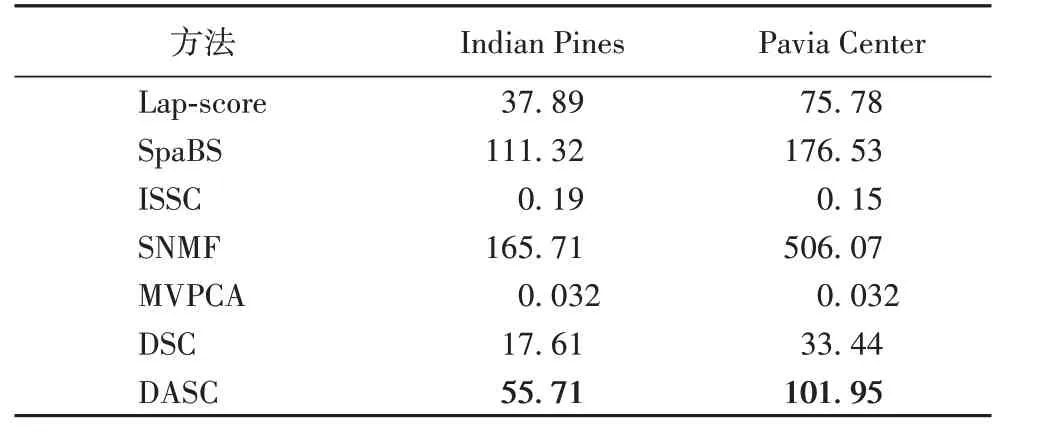
表2 波段数为20时不同方法的运行时间对比 单位:sTab.2 Running time comparison of different methods when the number of bands is 20 unit:s
由表2 可以看出,ISSC 和MVPCA 方法所用时间较少,SpaBS 和SNMF 方法计算效率较低,DSC 和DASC 的计算效率适中。同时结合分类精度和实验效果来看,DASC的综合表现最好,具有很好的应用价值。
4 结语
本文提出使用DASC 方法来实现高光谱波段选择。通过在编码器和解码器中引入自表达层来模仿传统子空间聚类的“自表达”属性,充分运用光谱信息和非线性特征转换得到波段之间的相互关系,并且将深度子空间聚类和生成对抗网络相结合,引入对抗学习来监督自编码器的样本表示和子空间聚类,使得子空间聚类具有更好的自表达性能。同时,加入拉普拉斯正则化来考虑反映图像几何信息的局部流形结构,使模型更加鲁棒。实验结果表明,DASC方法在波段选择上具有更好的效果,综合来看具有较高的应用价值。但是,由于该方法无法使用批梯度下降方法进行训练,因此在计算效率方面存在不足,这将是后续研究和改进的重要方向。

