压电陶瓷驱动的长行程快刀伺服机构设计

闫 鹏，李金银

(山东大学 机械工程学院 高效洁净机械制造教育部重点实验室，山东 济南 250061)

1 引 言

近年来，具有自由曲面的光学元件及其他精密复杂器件在军用、民用和空间探索等领域得到广泛应用[1-2]。由于此类自由曲面元件特殊的表面结构和其多自由度的特点，使用较少的元件即可实现更高的光学效率，从而使得系统具有成本低、结构简单、光学性能好、分辨率高等优点。然而光学自由曲面作为一种典型的非旋转对称曲面，具有不规则变化特征、没有固定的回转中心、形状复杂且对加工精度的要求极高，传统加工方法无法满足此类零件的高效、高精密加工。在超精密加工技术中兴起的快刀伺服技术(Fast Tool Servo，FTS)可以实现复杂曲面的高精度和高表面质量加工，具有高频响、高定位精度的特点，成为加工复杂曲面元件的高效手段[3-5]。

快刀伺服系统一般采用压电陶瓷[6-7]、音圈电机[8-9]、磁致伸缩驱动器[10]等作为驱动机构。与其他驱动器相比，压电陶瓷驱动器具有高刚度、大输出力、高分辨率的特点，能够实现快刀伺服系统的高频响和高精度加工性能，因此压电陶瓷驱动的快刀伺服机构得到广泛关注。然而，压电陶瓷的输出行程一般只有其自身长度的千分之一，传统的压电陶瓷型快刀伺服机构具有较高的固有频率，但其输出行程较小。Kim等[11]基于柔性铰链机构，采用堆叠式压电陶瓷驱动器设计了一种快刀伺服机构，用于补偿加工过程中的主轴运动误差。该快刀伺服机构运动分辨率0.15 μm，其运动行程只有数微米。Zhu等[12]采用压电陶瓷驱动，实现了一种超高固有频率的快刀伺服机构的设计和控制。得益于压电陶瓷和柔性铰链机构的使用，该机构具有5.35 kHz的超高固有频率，从而使得系统能够具有更高的带宽和频响性能，然而该系统行程也仅有数微米。压电陶瓷驱动的快刀伺服机构行程小的缺点使得应用该技术加工某些复杂曲面时面临困难，限制了快刀伺服技术的应用和发展。

为放大压电陶瓷的输出位移需要采用柔性放大机构，包括杠杆机构[13]、桥式机构[14]、Scott-Russell 机构[15]等。在这些柔性放大机构中，杠杆机构由于机构简单、放大比稳定等特点在快刀伺服机构的设计中得到广泛应用。Wang等[16]基于杠杆放大原则设计了柔性放大机构应用于快刀伺服系统，实现快刀伺服机构的长行程输出。然而杠杆机构的非对称性会产生寄生位移，影响曲面加工精度。为了补偿杠杆放大机构产生的寄生位移，Liu[17]设计了一种长行程快刀伺服机构，该机构单独设置一组驱动用以补偿放大机构产生的寄生位移，然而该机构增加的驱动单元给机构的控制带来挑战，增加了系统的复杂度。

为实现压电陶瓷驱动的快刀伺服机构的长行程输出性能并消除机构的寄生位移，本文基于杠杆放大原则，设计和分析了一种压电陶瓷驱动的长行程快刀伺服机构，并对该机构进行了有限元仿真和实验验证。有限元仿真和实验结果表明，该机构能够实现100 μm的长行程位移输出，同时消除了寄生位移，能够保证良好的加工精度。

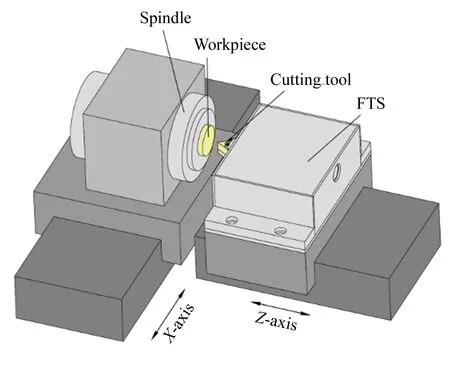
图1 FTS加工原则Fig.1 Working principle of FTS

2 机械结构设计

快刀伺服整体加工系统如图1所示，工件安装在空气主轴上，同时能够在x方向移动，快刀伺服机构安装在机床z轴的精密导轨上，金刚石刀具安装在快刀伺服机构上。在加工过程中，工件随主轴一同做旋转运动，金刚石刀具在快刀伺服机构的带动下，根据主轴旋转信号进行相应的直线往复运动，从而去除工件表面材料，完成曲面加工。

本文设计的压电陶瓷驱动的长行程快刀伺服机构如图2所示。柔性机构具有无摩擦、无需装配、结构紧凑的优点，可以实现压电陶瓷输出位移的放大和传递。在众多类型的柔性铰链中，直圆型柔性铰链与一般柔性铰链相比，旋转精度更高，因此在设计中采用了直圆型柔性铰链。

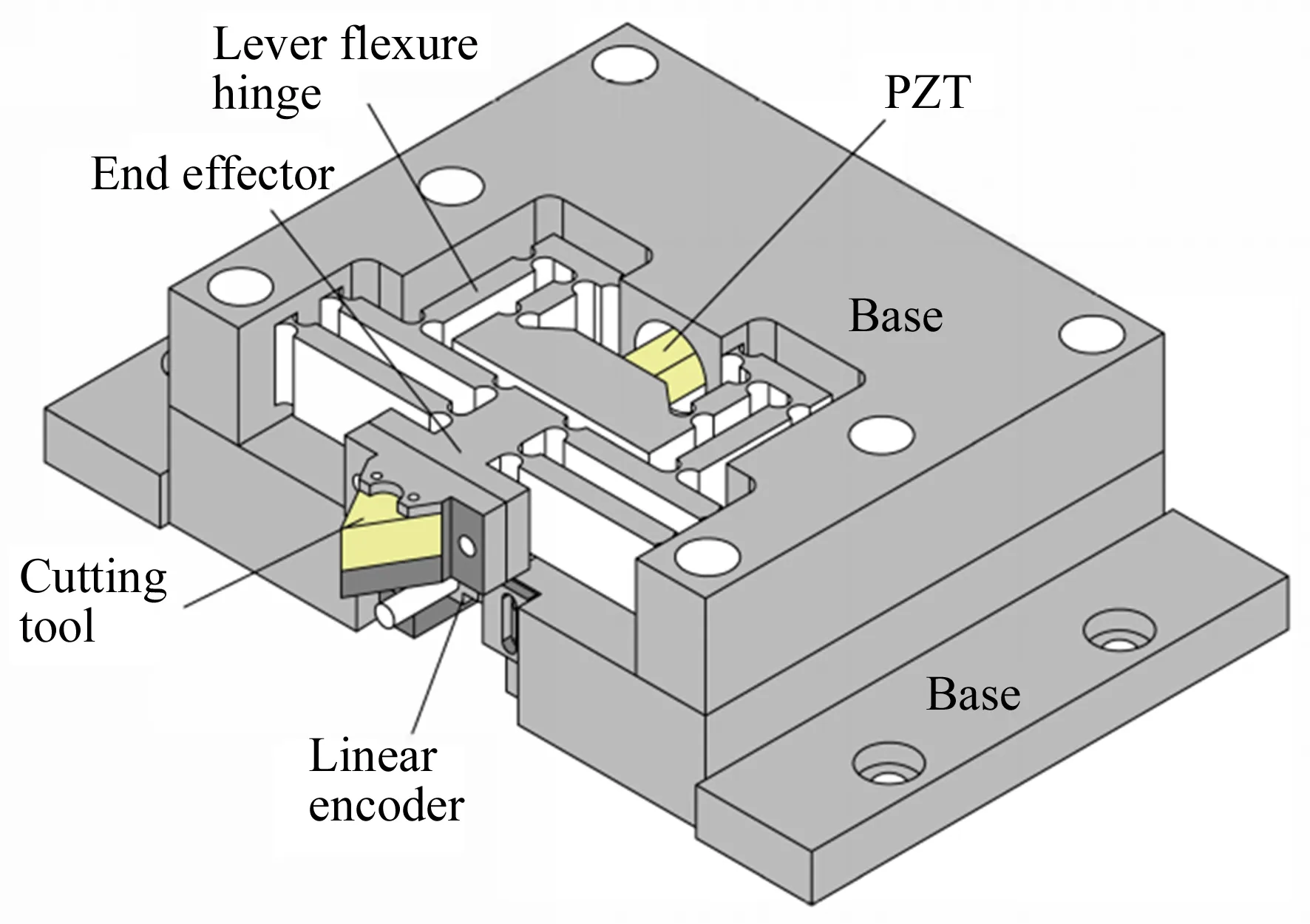
图2 FTS机械结构Fig.2 Mechanical structure of designed FTS

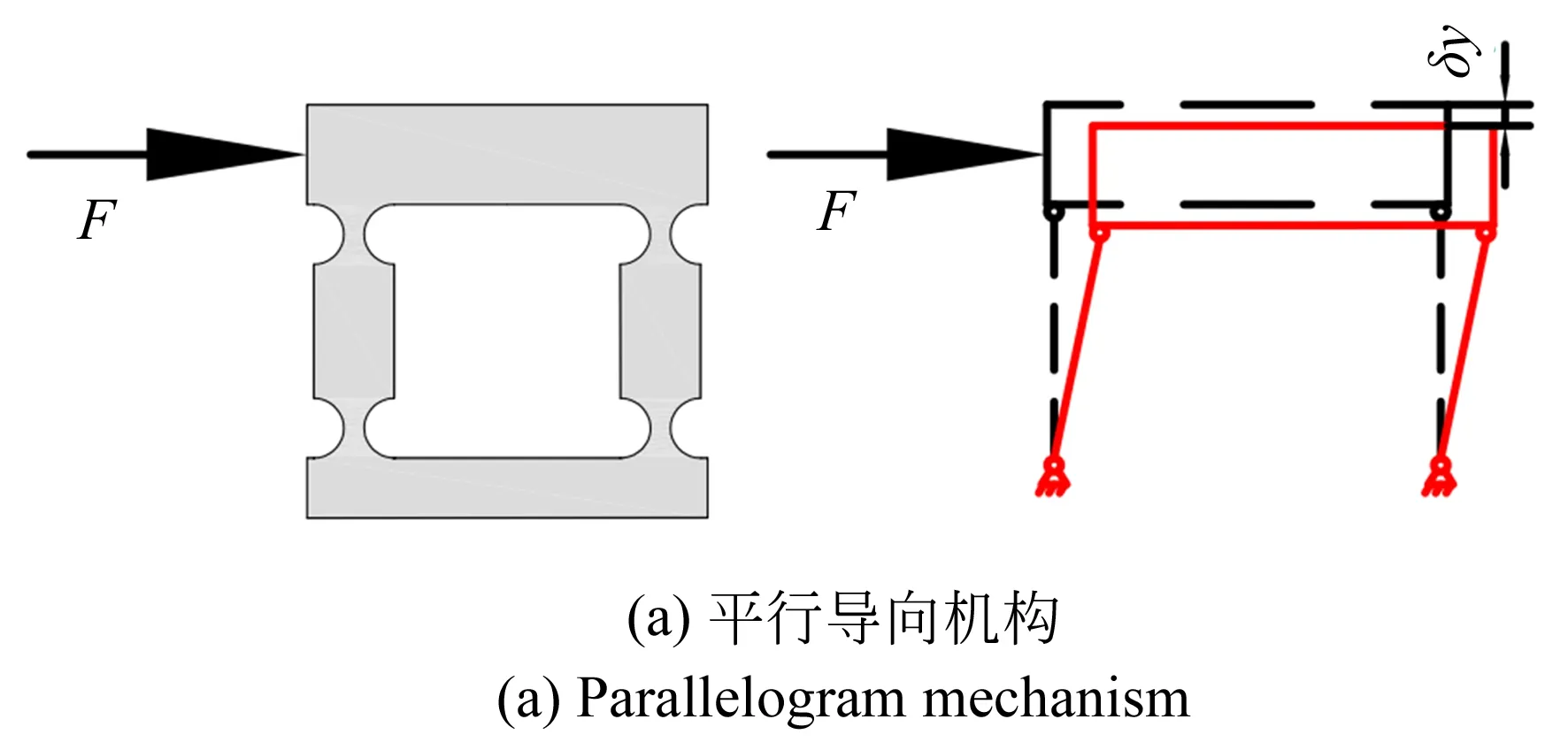
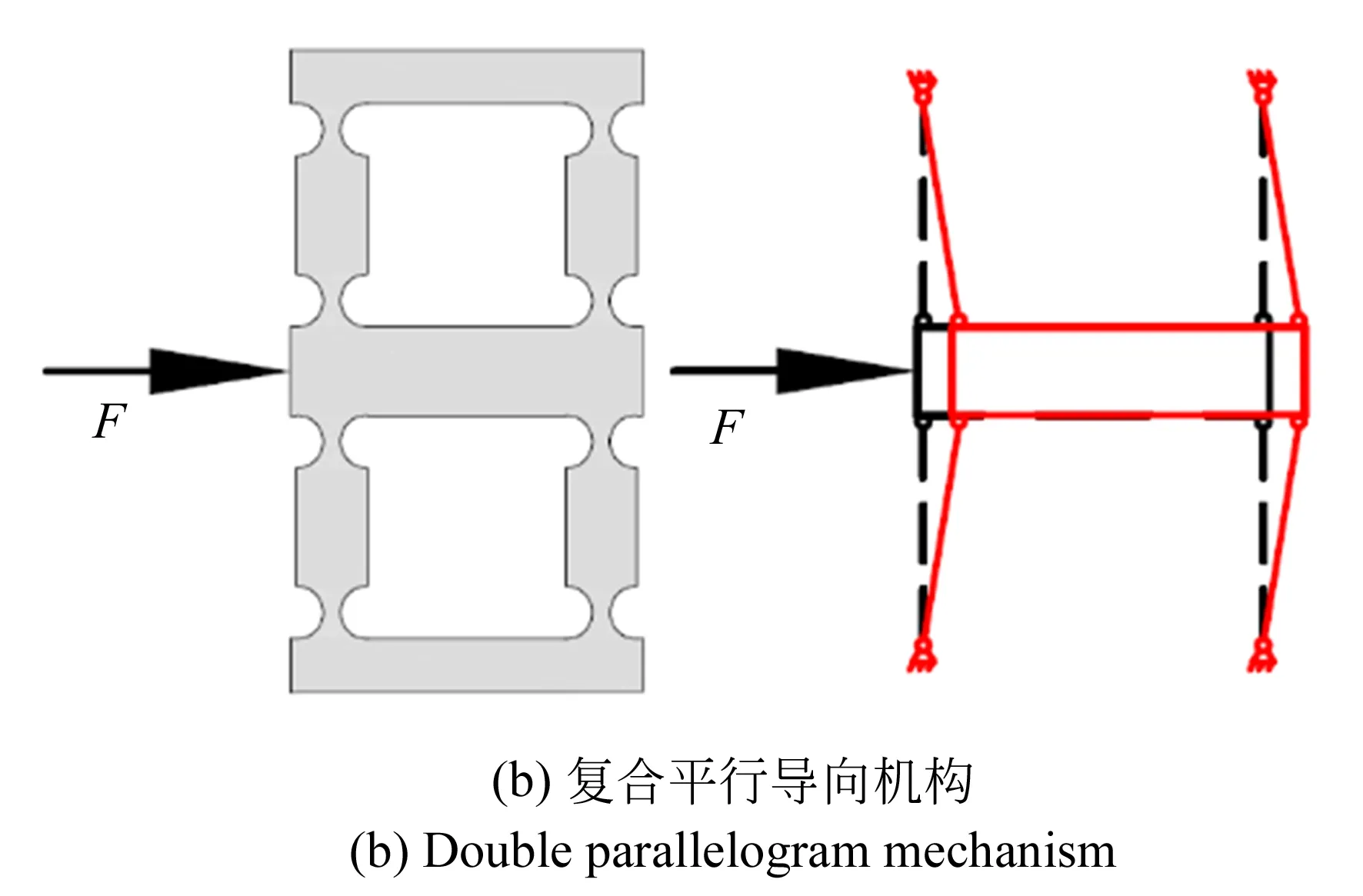
图3 本文采用的复合平行导向机构Fig.3 Double parallelogram mechanism

在压电陶瓷驱动的快刀伺服机构设计中，如何有效地抑制机构寄生位移的产生是提高系统加工精度的关键。如图3所示，平行导向机构结构简单，但在输出指定位移的同时会产生一定的寄生位移。因此在设计时采用了复合平行导向机构，其对称性结构能消除寄生位移，增加机构输出端水平和垂直方向的刚度。

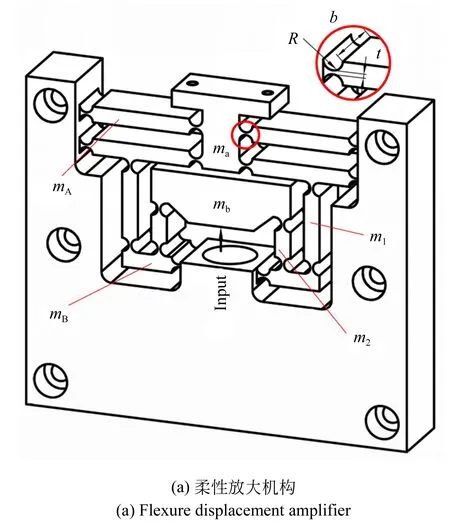
图4 柔性放大机构及其原理Fig.4 Flexure displacement amplifier and its schmatic diagram

为实现快刀伺服机构的长行程输出性能，需要采用柔性放大机构来放大压电陶瓷驱动器的输出位移。本文设计了一种对称式的二级杠杆放大机构，如图4所示。压电陶瓷输出位移，通过柔性放大机构进行放大，最终通过复合平行导向机构在末端运动平台输出位移。一方面，二级杠杆放大机构使得机构实现放大功能的同时结构更加紧凑，输出端的放大杠杆也具有一定的导向作用，进一步精简快刀伺服机构的机械结构。另一方面，整个放大机构采用对称式结构，能够在输入端消除非工作方向的寄生位移，提高输出精度。

3 理论建模和有限元仿真

3.1 机构动力学建模

根据伪刚体模型，本文设计的长行程快刀伺服机构可以等效为弹簧-质量-阻尼系统，如图5所示。其中，Ke和Kpzt为柔性机构和压电陶瓷的等效刚度，ce和cpzt是柔性机构和压电陶瓷的等效阻尼系数，M是机构的等效质量，Fpzt是压电陶瓷驱动力。

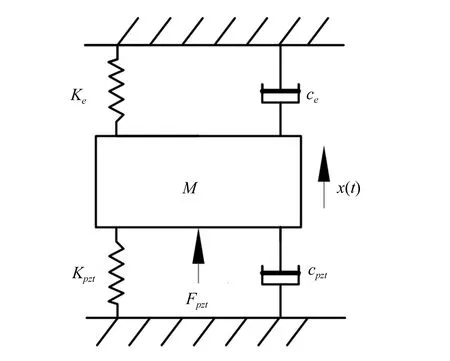
图5 等效动力学模型Fig.5 Equival dynamic model

本文设计的长行程快刀伺服机构只在平面内运动，对于机构设计中采用的直圆铰链，只考虑其在平面内的变形，基于柔度矩阵方法[18]，其输出可简化为:

(1)

式中：Δxi和Δyi分别为直圆铰链在平面内沿x向和y向的形变，Δα为直圆铰链绕z轴的转动角度。假设直圆铰链理想旋转，即忽略直圆铰链弹性变形下的位移，只考虑直圆铰链的旋转刚度，可得:

(2)

式中kR为直圆铰链的旋转刚度。

用拉格朗日原理分析机构的动力学模型，此机构的等效动能为:

(3)

式中：nA=4，nB=2，分别代表输出端和输入端连杆的数量，x代表输出端位移，ma,mb代表输出端和输入端平台质量，m1,m2代表次级放大和初级放大机构处连杆的质量，IA,IB分别代表输出端和输入端连杆的转动惯量：

(4)

(5)

其中mA，mB分别代表次级放大和初级放大杠杆的质量，分别为：

mA=ρ(l2·b·(2R+t)-πR2b)，

(6)

mB=ρ((l4+3R+t/2)·b·(2R+t)-πR2b).

(7)

机构的弹性势能为：

(8)

式中：n1=10，n2=8，分别代表输出端和输入端直圆铰链个数，θ1，θ2分别代表输出端和输入端铰链的旋转角度：

(9)

(10)

忽略等效动力学模型中的阻尼影响，对设计的长行程快刀伺服机构应用拉格朗日方程可得：

(11)

系统的动力学方程为：

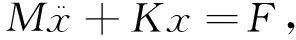
(12)

其中：

(13)

(14)

由此可得机构的固有频率:

(15)

忽略压电陶瓷预紧力对机构输出行程的影响，机构的最大输出位移为:

(16)

式中：Xn为压电陶瓷的最大输出行程，X为机构的最大输出行程。

在上述分析中，机构的行程输出随着直圆铰链的旋转变形增大而增大。然而值得注意的是，随着直圆铰链的旋转变形增大，变形应力也随之增加，铰链的变形应力会影响机构的使用可靠性。对于直圆铰链，其最大应力和最大旋转变形的关系[19]为：

(17)

式中:β=t/2R，f(β)为一无量纲因子:

(18)

3.2 参数设计和有限元仿真

在快刀伺服机构的设计中，实现长行程输出的同时必然会降低机构的固有频率，影响系统带宽和系统加工效率，因而在机构设计时需要综合考虑行程和固有频率性能选择机构参数。

本文所设计的长行程快刀伺服机构材质选用具有优越变形能力的铝合金AL-7075，材料特性如表1所示。根据上述理论分析，结合所设计机构的行程和固有频率频率指标，同时考虑机构的应力及尺寸，选择机构参数如表2所示。

为验证所设计机构的性能及理论分析的有效性，采用ANSYS软件对所设计机构进行有限元仿真。对机构施加450 N输入力时机构的位移变形如图6所示。

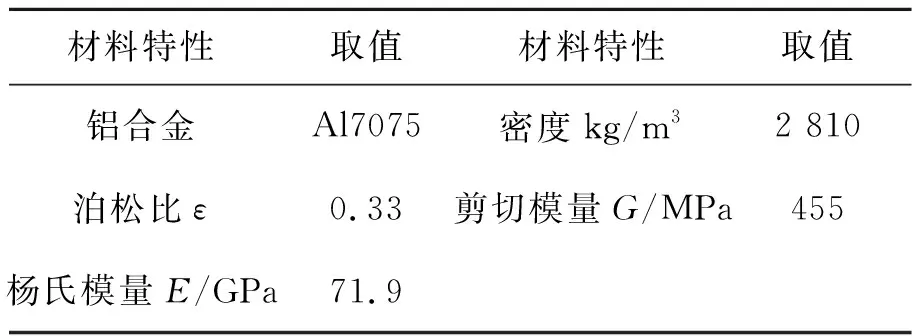
表1 机构材料参数

表2 机构参数

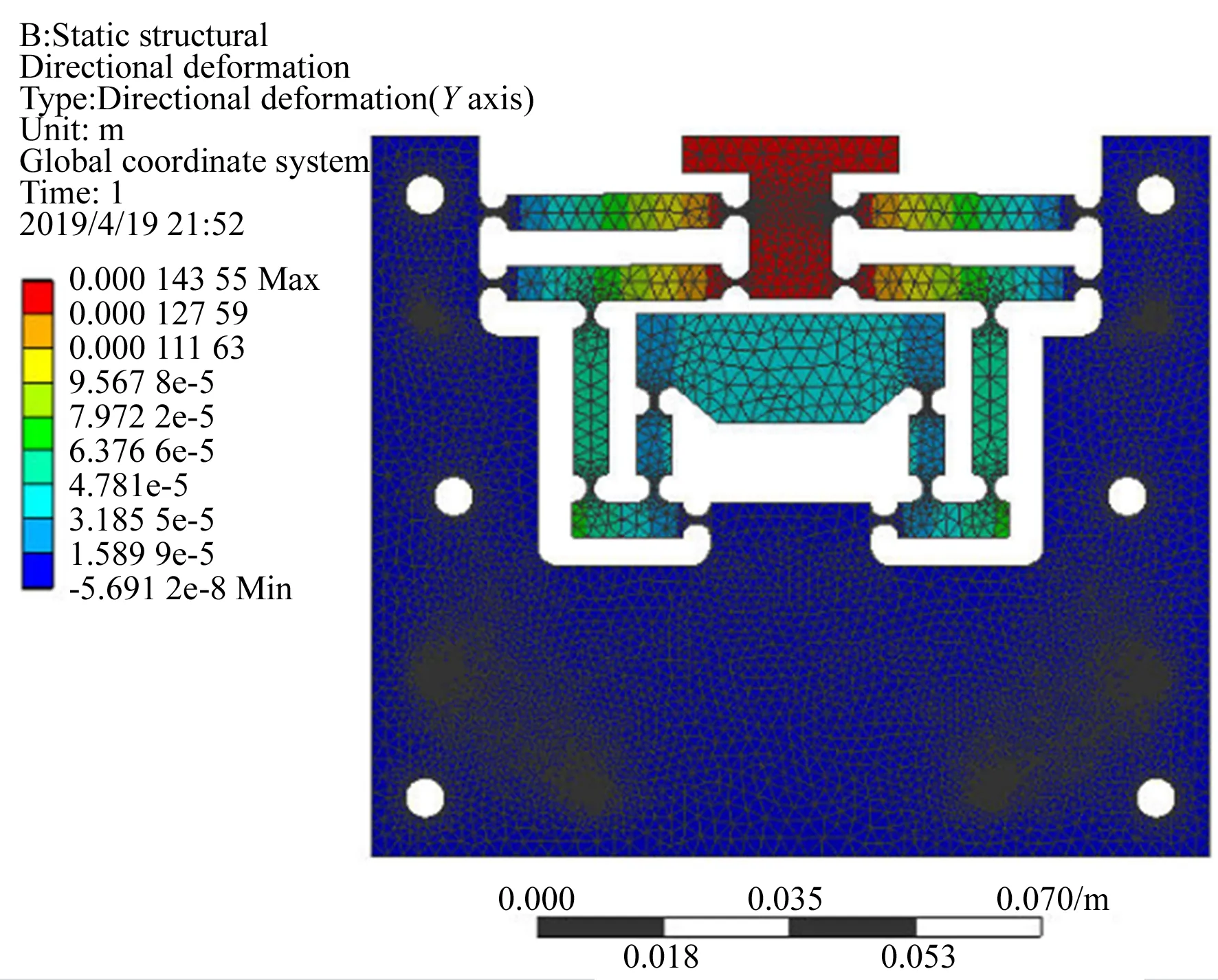
图6 FTS机构位移变形Fig.6 Displacement deformation of designed FTS

从仿真结果中可知对称布置的机构设计消除了非工作方向的寄生位移。进一步的，对机构进行有限元模态分析，有限元仿真和理论计算得到的机构刚度和一阶固有频率结果如表3所示。理论计算和有限元仿真结果基本一致，验证了理论模型的有效性。

表3 有限元仿真值与理论值对比

Tab.3 Comparison between FEA and theoretical results

理论值有限元值误差等效刚度2.9 N/μm3.1 N/μm6.4%一阶模态678 Hz689 Hz1.6%

4 实验测试

以优化设计的机构参数，采用超精密线切割的方式对所设计的长行程快刀伺服机构进行了加工，并建立了如图7所示的实验系统。实验中采用Noliac公司的压电陶瓷(NAC2014-H28)，其最大行程42.9 μm，采用线性光栅作为位移传感器。

图7 FTS系统实验装置Fig.7 Experimental setup of the designed FTS system

4.1 静态性能实验

对系统施加0～110 V的正弦波电压信号，得到机构的输出行程特性，如图8所示。设计的快刀伺服机构可以达到100 μm的行程输出，这一行程可以满足大多数光学自由曲面的加工。

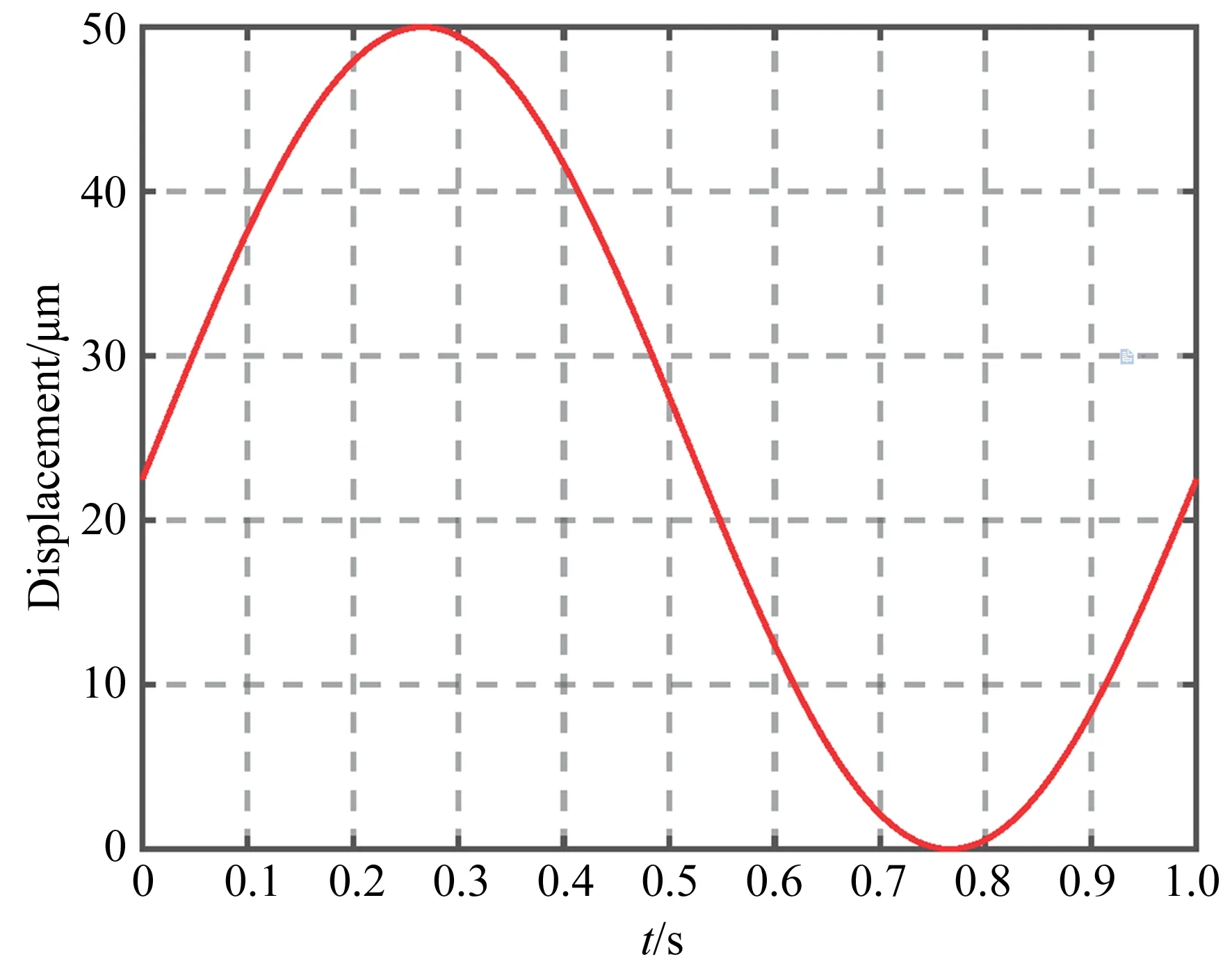
图8 FTS机构行程测试Fig.8 Stroke test of the designed FTS

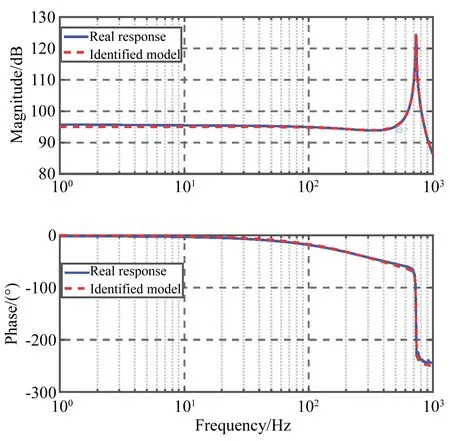
图9 实际系统和辨识系统的频率响应Fig.9 Frequency responses of real and identified models

4.2 动态性能实验

为得到系统的动力学模型，对压电陶瓷施加1～1 000 Hz的正弦扫频信号，采用DFT实时控制算法得到系统的频率响应数据，进一步辨识得到实验系统的动力学模型，如图9所示。

辨识得到系统的传递函数模型如式(9)所示：

G(s)=

(19)

系统的动态实验得到其固有频率为730 Hz，略高于理论和仿真值，这是由于加工及安装误差增大了系统的刚度和固有频率。在此固有频率下，系统可以实现较高的带宽和频率响应，从而保证系统的加工效率。

4.3 闭环跟踪实验

对图1所示的加工系统，采用坐标转换法，则待加工自由曲面z=f(x，y)在柱面坐标系(ρ，θ，z)中可表示为：

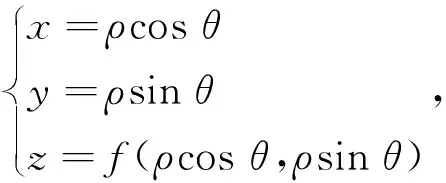
(20)

其中：ρ为工件沿x轴的位移，θ为主轴的旋转角度，z为刀具在快刀伺服系统带动下沿z轴的进给位移。

图10 轨迹跟踪和跟踪误差Fig.10 Trajectory and tracking errors

在上述加工过程中，系统常常需要跟踪连续的正弦信号。为了评估系统的跟踪性能，实验跟踪幅值25 μm、频率50 Hz的正弦信号。根据式(19)得到的系统动力学模型，采用基于PID镇定的并联内模方法对系统进行闭环控制[20]，实验结果如图10所示。对50 Hz信号的跟踪误差为±90 nm，为其行程的0.36%，验证了系统具有良好的跟踪性能。

5 结 论

本文设计了一种压电陶瓷驱动的长行程快刀伺服机构，采用对称式结构及二级放大机构，实现了压电陶瓷驱动的快刀伺服机构的长行程输出性能并消除了非工作方向的寄生位移。

针对所设计的长行程快刀伺服机构，采用伪刚体模型和拉格朗日原理建立了机构的动力学模型，并对设计的机构进行了有限元仿真和实验验证，仿真和实验结果与理论模型有良好的一致性。实验验证表明本文设计的快刀伺服机构兼顾了机构的行程和固有频率性能，可以达到100 μm的行程输出，同时具有730 Hz的固有频率。闭环跟踪试验也验证了系统良好的信号跟踪性能。

本文设计的压电陶瓷驱动的长行程快刀伺服机构对提升快刀伺服机构的应用范围和加工精度具有参考意义。