基于需求响应的铁路集装箱班列始发时刻优化

江雨星，高翠香，牛惠民

(1.兰州交通大学 交通运输学院，甘肃 兰州 730000；2.北京交通大学 远程与继续教育学院，北京 100044)

制定合理的铁路集装箱班列始发时刻是铁路集装箱运输组织的重要工作。随着“一日一图”列车运行组织模式的实行，集装箱班列始发时刻的确定，不仅需要根据铁路集装箱办理站和邻接线路的技术条件，还要综合考虑当日集装箱货物到达办理站的时刻和数量，即所制定的列车开行计划尽可能适应货物的需求特征，这是铁路改进货运服务质量、迎接市场竞争的必然选择。

集装箱班列始发时刻优化属于货物列车运行图优化问题。目前，国内外许多学者对货物列车运行图的优化进行了研究。文献[1]在旅客列车运行线已定的情况下，研究了如何加入货物列车运行线，运用拉格朗日松弛算法对建立的线性整数规划模型进行求解。文献[2]针对货物列车在路网中运行径路固定与不固定2种情况，建立了列车运行图优化的混合整数规划模型。文献[3—4]研究了货物列车运行图与机车周转的协同优化问题。

随着用户对铁路服务质量要求的不断提高，基于需求响应的列车运行图优化是近年来的研究热点，尤其在旅客列车方面，已取得较为丰富的成果。文献[5]依据时变的客流需求及给定的停站模式，以旅客候车时间最少为目标构建了二次整数规划模型。文献[6]研究了基于需求驱动的地铁列车时刻表优化问题。文献[7]在编制列车运行图时，综合考虑了旅客需求和企业利益。文献[8]针对列车间非定序越行的情况，建立了基于客流需求响应的时刻表优化模型。对于需求响应下货物列车运行图的优化，还少有文献进行研究，但已有学者考虑了货物与列车的复杂匹配关系。文献[9]在列车始发时刻给定的前提下，充分考虑了货主托运货物的数量、出发时间等因素，以货物停留时间最小为目标，构建了整数规划模型，实现不同货物与列车之间的最优匹配。

综上，既有货物列车运行图的研究成果，主要集中在通过建立数学模型及求解算法，解决不同列车对车站、区间占用的时空冲突问题，但没有考虑货流的需求，这样得到的货物列车运行图，会造成车站“货物排队”或“有线无车”的现象。在旅客列车运行图的优化研究中，已有很多学者考虑了客流需求，但铁路旅客运输与集装箱货物运输之间存在很大差异，现有的旅客列车运行图研究理论无法解决基于需求响应的集装箱班列始发时刻优化问题。

对于运输时效性要求较高的集装箱班列，现有研究主要集中在班列开行方案设计和集装箱装载方案优化方面。文献[10]以成本最小为目标，建立了集装箱班列开行方案优化的整数规划模型，将集装箱有效地分配到开行的直达和中转班列上。文献[11]研究了铁路集装箱班列开行方案与价格制定综合优化问题。文献[12]以单层集装箱班列为研究对象，构建了装载方案优化的混合整数规划模型。文献[13]针对于双层集装箱班列，探讨了不同类型集装箱的装载方案。目前，还未有文献考虑过集装箱班列始发时刻的优化问题。

本文将依据铁路集装箱货物运输需求，充分考虑集装箱货物与班列在时间和数量方面的匹配关系，构建铁路集装箱班列始发时刻优化的非线性混合整数规划模型，结合模型特点，设计基于遗传算法的求解方法，优化基于需求响应的铁路集装箱班列始发时刻。

1 问题描述及假设

以1个大型铁路集装箱办理站为例，每天有大量的集装箱货物(以下简称为集装箱)通过公路交通运送至该站，并在发送箱区进行集结，集结至要求的数量后，在集装箱装卸线上装入开往目的站的集装箱班列。对于这种运量大、货源相对稳定的集装箱运输问题，货物需求主要体现在各批集装箱送到办理站的时间和数量。基于此，本文优化班列始发时刻的主要依据就是这些集装箱送达办理站的时间和数量，该信息可通过铁路集装箱运输管理信息系统获得。

集装箱班列始发时刻对需求的响应，表现为班列运行线的分布要尽可能与动态的集装箱需求相吻合。班列选择不同的出发时刻，将导致集装箱等待时间、班列装车时间均会发生变化。如图1所示，当第q-3，q-2和q批集装箱由第j班列承运时，班列出发时刻Tj与这3批集装箱到站时刻τq-3，τq-2和τq的间隔，要满足装车作业时间和出发技术作业时间的要求。

铁路货物运输中，任意1批货物只能由1列车运送。为满足集装箱班列编成箱数的要求，对于相邻到达的2批集装箱，其与班列间的最优匹配不一定遵循通常的“先到先服务”原则。如图1中，对于第j班列，承运第q-3和q-2批集装箱后，剩余承运能力小于第q-1批集装箱的数量，但大于等于较晚送达的第q批集装箱的数量，此时该班列将承运第q批集装箱，而第q-1批集装箱由后出发的第j+1班列承运。

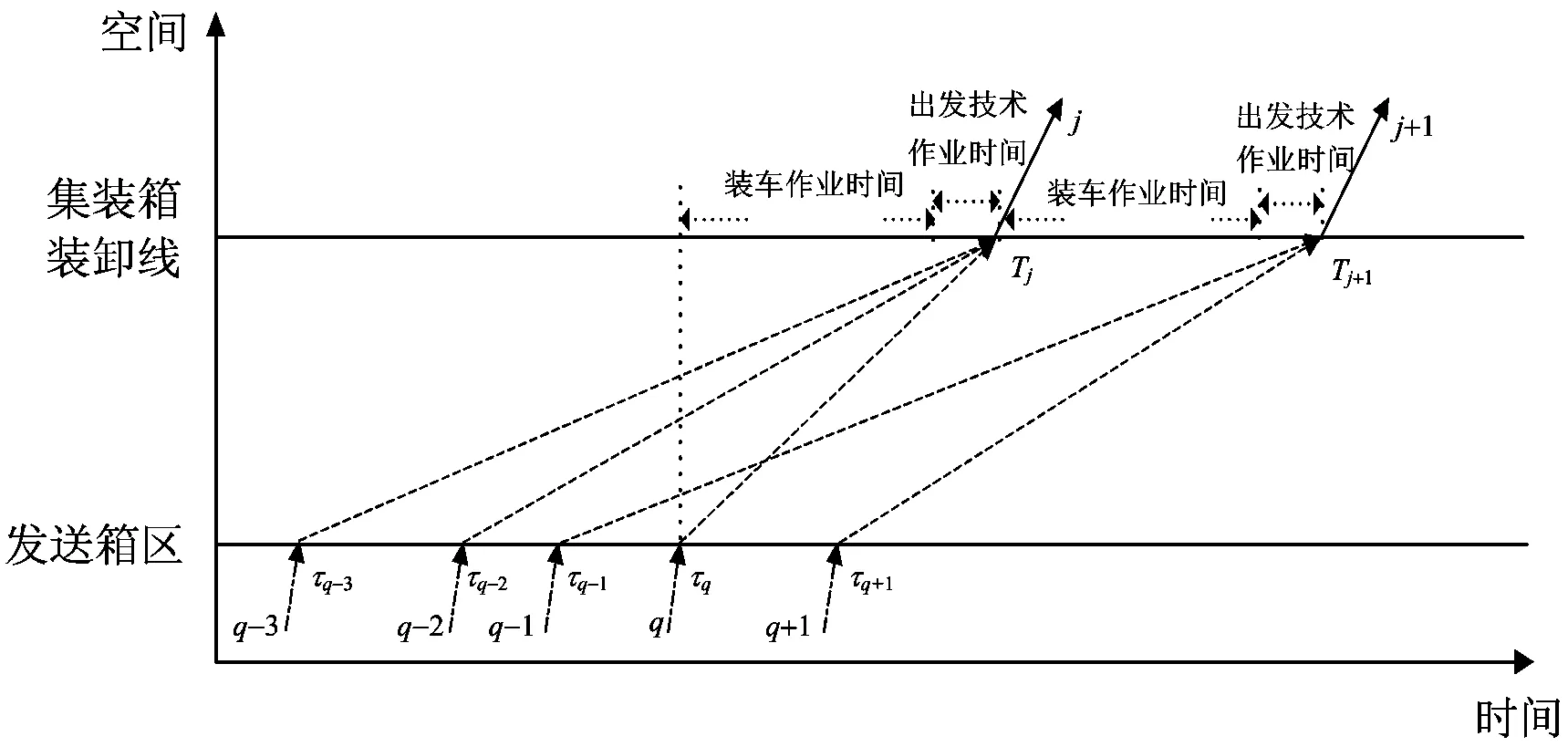
图1 集装箱与班列匹配示意图

可见，在时间及数量双重条件的约束下，集装箱与班列的匹配关系会非常复杂，从而极大地增加了铁路集装箱班列始发时刻优化的难度。为构建优化模型，做以下假设。

(1)在铁路集装箱办理站，集装箱到达、集结和装车等作业都是滚动的，对于较晚到站的一些集装箱，可能当天无法被运走。考虑这一情况，假定每天的最后时刻总有1列虚拟班列出发，用以承运当天未能运走的剩余集装箱，并对装载至该虚拟班列的集装箱赋予较大的等待时间权重。

(2)集装箱货物均由20英尺的标准集装箱装载，每批到达办理站的集装箱数量不大于班列的最大编成箱数。当集装箱数量大于最大编成箱数时，将其分割为多批，使任何1批都满足假设条件。

2 优化模型构建

2.1 参数定义

定义如下符号和参数：Q为在24 h(1 d)内送达办理站的集装箱批次集合，Q={1,2,…,q,…,m-1,m}，其中m为集装箱总批数；J为集装箱班列序号集合，J={1,2,…,j,…,k-1,k}，其中k-1为实际开行的集装箱班列数量，k为虚拟班列；nq为第q批集装箱的箱量，箱；tz为单个集装箱的平均装车作业时间，min；tf为集装箱班列办理出发技术作业时间，min；Nmax和Nmin分别为集装箱班列最大、最小编成箱数，箱；M为充分大的正数。

通常情况是在集装箱班列开行数量给定条件下，需要确定集装箱与班列之间的最优匹配。为确保运输能力充足，可依据式(1)给定实际开行的班列数量，再根据下文的数学模型优化班列始发时刻。

(1)

2.2 优化模型

1)约束条件

(1)集装箱装车唯一性约束：任意1批集装箱只能由1列班列运输。

(2)

(2)集装箱班列编成箱数约束：班列的编成箱数应在[Nmin,Nmax]范围内。

(3)

(3)作业时间约束：班列出发时刻与其承运集装箱到站时刻的间隔要满足装车作业时间和出发技术作业时间的要求。

q∈Q,j∈J{k}

(4)

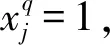
(4)集装箱班列发车间隔约束：承运同一目的站集装箱的班列，需要在同一条集装箱装卸线上办理装车作业和出发技术作业，因此，第j班列发车后，第j+1班列才能开始进行装车，则相邻2列班列的发车间隔要满足后一班列的作业时间要求。

j∈J{k-1,k}

(5)

2)始发时刻优化模型

以集装箱在办理站总停留时间Z最小为目标函数，以式(2)—式(5)为约束条件，建立的基于需求响应的铁路集装箱班列始发时刻优化模型为

(6)

s.t.

式(2)—式(5)

当集装箱在办理站总停留时间最小，所对应的班列始发时刻即为得到的优化结果。需要说明的是：为使到达办理站的集装箱尽可能当天装车运走，应对剩余至第2天的集装箱赋予较大的等待时间惩罚，参照铁路旅客车站等待时间的近似计算方法[5]，本文在优化过程中假定虚拟班列延误半天，即该班列的始发时刻Tk=1 440+720=2 160。

3 算法设计

3.1 精确求解

上述模型是一个非线性混合整数规划问题，且约束条件为线性。运用Gurobi求解器可以对构建的模型进行精确求解，结果见表1。

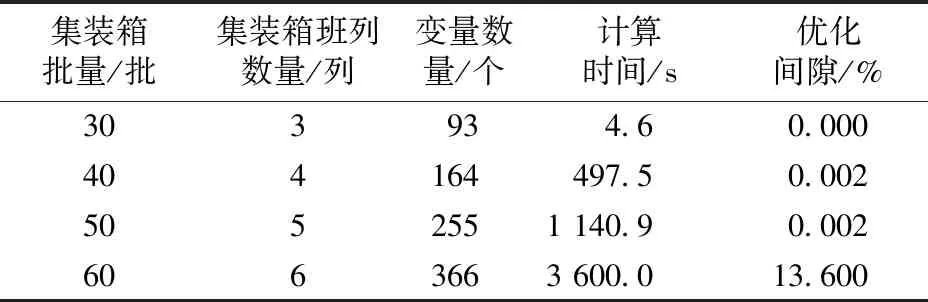
表1 不同规模算例的Gurobi计算时间及优化间隙

由表1可知，当集装箱为30批、班列数为3列时，Gurobi在4.6 s内即可得到最优解，当集装箱和班列数量分别增加到60批和6列，求解时间达1 h时仍未获得最优解。显然，随着集装箱和班列数量的增加，运用Gurobi这类求解软件很难得到问题的最优解。

3.2 遗传算法设计

遗传算法是一种基于随机搜索的群体智能算法，具有较高的求解效率，并多次用于列车运行图的计算问题[4,14]。因此，本文将运用遗传算法求解构建的数学模型。算法的核心思想，是在满足集装箱班列编成箱数、装车作业时间、发车间隔约束的基础上，通过交叉、变异等操作对集装箱与班列匹配关系进行不断改变，从而寻找班列最有利的始发时刻。

3.2.1 染色体编码

为避免染色体过长影响计算效率，本文采用整数编码方案。每个染色体由2部分组成：第1部分是集装箱与班列的匹配关系，所含的基因数量等于集装箱总批数，其位置顺序为集装箱批次，取值为班列的序号，如图2所示，第1部分中第2个基因的值为3，表示第2批集装箱由第3列班列承运；第2部分为各集装箱班列的始发时刻，所含的基因数量等于班列数量，其中最后1个基因取值为2 160，其余基因的取值为[0,1 440]间的整数，如第2部分中第3个基因值为420，表示第3列班列的始发时刻为420÷60=07:00。

图2 染色体编码方案示意图

显然，采用上述编码方案，可使染色体在遗传操作过程中始终满足集装箱装车唯一性约束。

3.2.2 初始种群

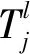
1)随机方案

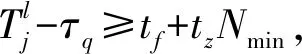
j∈J{k}

(7)

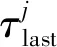
2)遵循“先到先服务”的方案

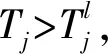
例如：在时间段[0,60]内，有10批集装箱陆续到达办理站，相关参数见表2；班列编成箱数Nmax=10，Nmin=5，单个集装箱平均装车作业时间tz=1 min，出发技术作业时间tf=5 min；班列数量为4，其中第4列为虚拟班列，给定其始发时刻T4=60+30=90。

表2 集装箱批次、数量及时间信息

在满足班列编成箱数的约束下，对于第1班列，承运集装箱的方案共有3种，分别是承运第1和第2批集装箱(共6箱)、第1批至第3批集装箱(共8箱)、第1批至第4批集装箱(共10箱)。采用最后1批集装箱标号表示相应的方案，则第1班列承运方案如图3中的j=1所示。当第1班列承运第1和第2批集装箱时，第2班列承运方案(j=2)有2种，分别是承运第3批至第5批集装箱(共8箱)、第3批至第6批集装箱(共10箱)。以此进行推算，直至确定出各班列承运集装箱的所有情况。如图3所示，其中方案2-5-8-10的具体意义为：第1班列承运第1和第2批集装箱，第2班列承运第3批至第5批集装箱，第3班列承运第6批至第8批集装箱，第4班列承运第9和第10批集装箱，即这2批集装箱未能运走剩余至下一时段。

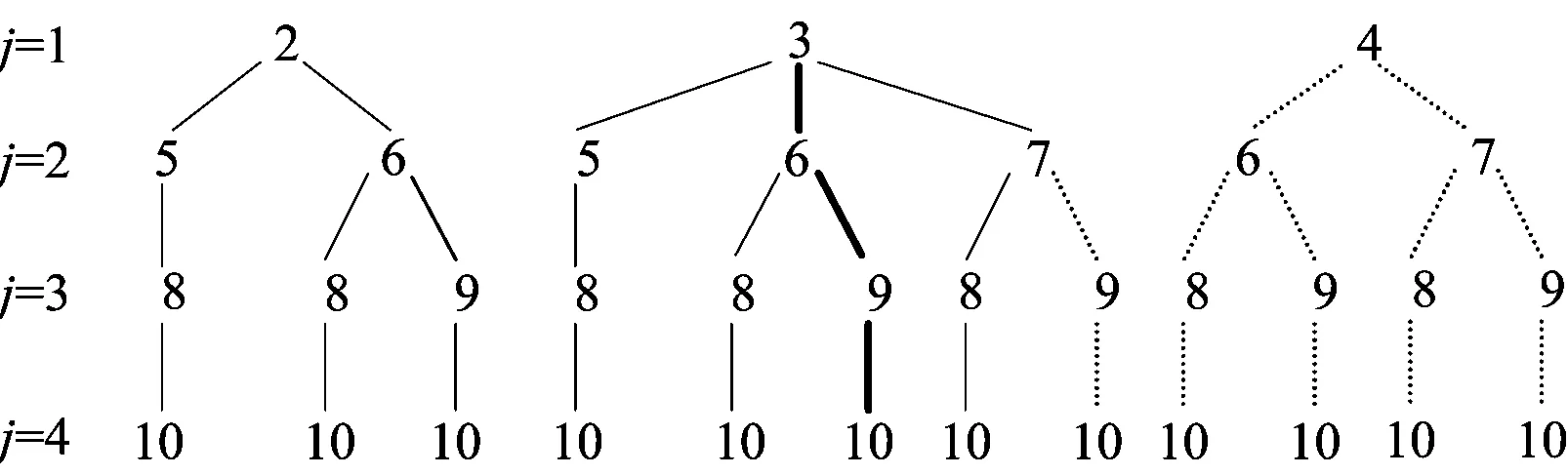
图3 搜索过程示意图

考虑到集装箱送达办理站的时间和数量具有一定的随机性，在严格遵循“先到先服务”原则下，也有可能不存在满足约束的可行方案。对于这种情况，初始种群仅由随机方案组成，不加入遵循“先到先服务”的方案。

3.2.3 染色体修复

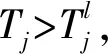
3.2.4 遗传算法流程

设计遗传算法流程如下。

Step1：生成初始种群。

Step2：令目标函数的倒数为适应度函数，将当前所有染色体带入适应度函数计算适应度值。

Step3：选择操作。为避免优秀个体在交叉、变异中被破坏，采用轮盘赌与精英保留相结合的策略进行选择。

Step4：交叉操作。在其中1个染色体中，随机选取表示匹配关系的1个基因，将其与之后的所有表示匹配关系的基因与另一个染色体中相同位置的基因进行互换，修复不可行染色体。

Step5：变异操作。在执行变异操作的染色体中，任意选取1个表示匹配关系的基因，改变该基因的取值，修复不可行染色体。

Step6：判断循环终止条件，若迭代次数没有达到设定的最大循环次数，则转Step2；否则算法结束，输出结果。

4 求解算例

4.1 参数输入

以胶州中铁联集青岛集装箱中心站开往黄岛的集装箱班列为例，采用本文提出的方法进行仿真计算。在所选择1 d的时间段内，共有100批集装箱陆续送达青岛集装箱中心站，相关数据见表3。班列最大编成箱数为50箱，最小编成箱数为40箱，根据式(1)可确定需组织开行10列集装箱班列进行承运。办理出发技术作业的时间为20 min，单个集装箱平均装车作业时间为2 min。

表3 集装箱批次、数量及时间信息

4.2 求解结果

运用Matlab2014编程对算例进行测试，种群规模取100，交叉概率取0.95，变异概率取0.1，迭代次数为1 500次。计算过程中适应度函数值的变化如图4所示，在运行了132 s后得到最终解，其适应度值为9.863 2×10-6,目标函数值为101 387 箱·min。由图4可知，随着迭代次数的增加，适应度函数值逐渐增加，在750次以后，适应度值已无明显变化，表明算法的收敛性良好。本文还运用Gurobi对该算例进行了求解，运算到7 200 s时，仍未找到最优解。可见，对于大规模问题，遗传算法能在较短时间内获得优化解，在计算效率方面具有明显的优势。

图4 适应度函数值变化

优化得到的各集装箱班列始发时刻及承运集装箱的批次和数量见表4。由表可知：第11行为虚拟班列，其承运的第99和第100批集装箱，是当天未能运走的剩余集装箱；部分集装箱与班列的匹配不遵循“先到先服务”，例如，第15批集装箱由第2列班列承运，而较早送达办理站的第14批集装箱由后出发的第3列班列承运。

比较表3和表4可知，集装箱班列始发时刻与货物需求的变化规律是吻合的。例如：在00:00至14:11之间，大量的集装箱密集到达办理站，共有70批，总箱数为340箱，则组织开行了7列班列承运这些集装箱，即表4中的第1至第7列班列，显然这部分班列承运的集装箱数量基本达到最大编成箱数，且发车时间安排较为紧凑，相邻班列出发间隔时间均不超过2 h；而在14:11之后，箱量减少，且集装箱的平均到达间隔时间较大，相应的后续出发班列的间隔时间增大。

表4 基于需求相应的集装箱班列始发时刻

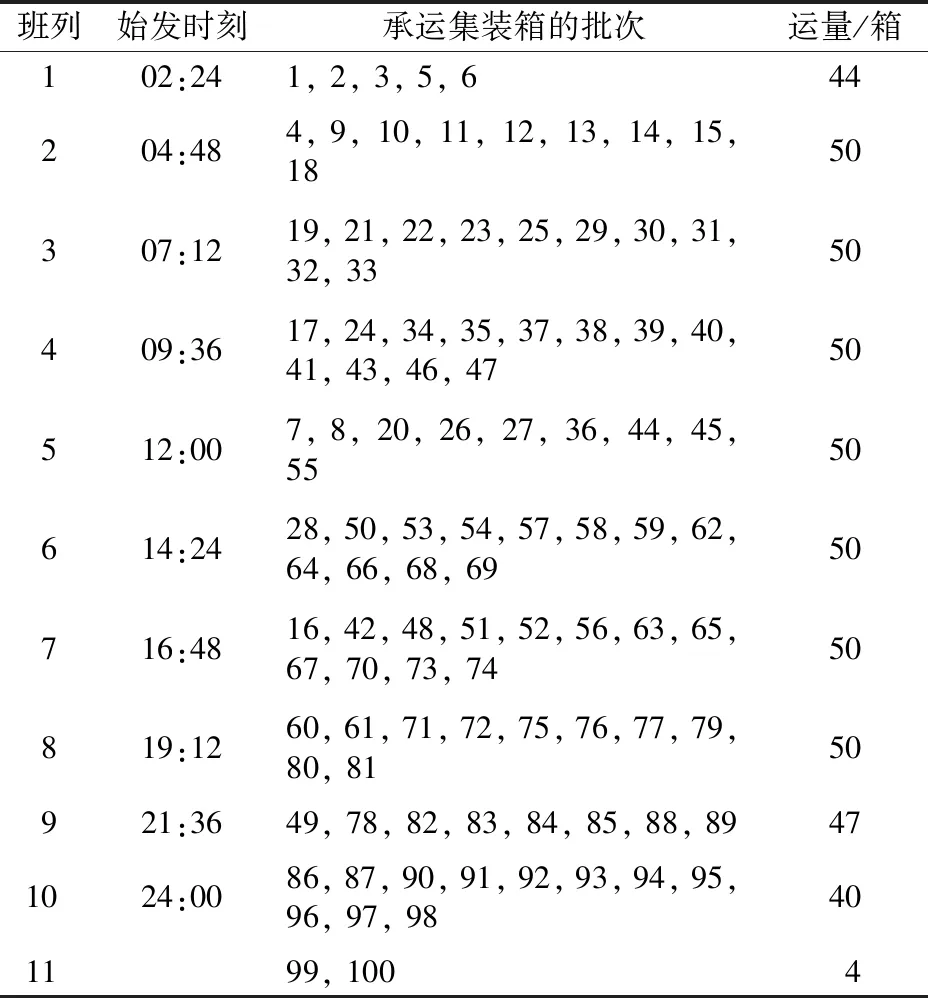
表5 均衡发车模式下集装箱班列始发时刻

以往研究在铺画列车运行线时，主要考虑列车出发的均衡性[15-16]。若采用均衡发车的模式，则算例中的青岛集装箱中心站每隔144 min(1 440÷10=144 min)组织发出1列开往黄岛的集装箱班列，从而可确定各班列的始发时刻，见表5。在此基础上，运用Gurobi计算得出各班列承运集装箱的批次，对应的集装箱最小总停留时间为131 655 箱·min。比较表4与表5方案的集装箱总停留时间，不难看出前者节省了30 268 箱·min。可见，利用本文模型及算法得到的集装箱班列始发时刻与集装箱货物的数量、到达时间分布之间具有较好的匹配性，使集装箱在办理站停留时间最短，说明制定的班列开行计划很好地响应了用户需求。

5 结 语

为解决铁路集装箱办理站发生的“货物排队”或“有线无车”问题，本文考虑了集装箱货物送达办理站的时间和数量分布特征，阐述了集装箱货物与班列的匹配规律，以集装箱货物在集装箱办理站的总停留时间最小为优化目标，构建了集装箱班列始发时刻优化的非线性混合整数规划模型。根据模型特点，设计了基于遗传算法的求解方法。通过算例测试，表明本文计算得到的集装箱班列出发时刻很好地响应了用户需求，可为铁路企业优化集装箱运输组织提供决策参考。