ARIMA模型和Holt-Winters方法在边坡土体深层水平位移预测中的比较
晏 凯, 吴佳晔, 张应迁, 杨 露
(1.四川轻化工大学管理学院,自贡 643000;2.四川升拓检测技术股份有限公司,自贡 643000;3.四川轻化工大学土木工程学院,自贡 643000;4.东北林业大学土木工程学院,哈尔滨 150000)
边坡稳定性问题一直是边坡工程的一项重要研究内容[1]。而边坡工程是一个不确定的、非线性的复杂的系统[2],目前国内外存在的边坡安全监测技术也是多种多样。如2010年Pieraccini等[3]、Barla等[4]、Gischig等[5]最早采用了GB-In SAR对边坡的变形进行监测研究;2012年阮志新等[6]利用测斜仪对高速公路边坡进行了监测并证明了监测的正确性;2013年王志勇等[7]利用In SAR技术对北京房山地区的滑坡进行了监测;以及2015年徐茂林等[8]利用TM30对鞍山市某露天矿边坡位移进行了监测实验,实现了自动化监测,等等。这些边坡工程监测方法大多都用于边坡变形分析,由此推断研究边坡变形对分析边坡稳定性意义重大。
土体深层水平位移是边坡变形监测中的重要指标之一。本文尝试运用ARIMA模型[9]和霍尔特-温特斯方法[10],对土体深层水平位移的历史数据进行短期预测和实证研究,并对结果加以比较,分析两种方法的优劣。
1 问题描述
1.1 方法选取的原则
在长期的边坡变形过程中,监测的土体深层水平位移值是随季节周期变化,并存在一定增长(或降低)趋势的非平稳时间序列。传统的预测方法如回归模型、k-最近邻分类的IBK模型等适用于平稳时间序列,对该类值的预测结果并不理想[11]。而由Box和Jenkins提出来的自回归求和滑动平均模型(ARIMA模型),是将非平稳时间序列先经过d阶差分平稳化,再对得到的平稳时间序列利用自回归[autoregressive, AR(p) process]和滑动平均过程[moving average, MA(q) process],并通过样本自相关系数(autocorrelation coefficient, ACF)和偏自相关系数(partial autocorrelation coefficient, PCF)等数据对建立的模型进行辨识,同时还提出了一整套的建模、估计、检验和控制方法[12];其次Holt-Winters预测方法,由于它可以同时处理趋势和季节性变化[13],并能适当地过滤随机波动的影响。因此选用ARIMA模型和Holt-Winters预测方法来预测具有季节性波动和趋势性增长(或减少)的非平稳时间序列问题,并对结果进行比较分析。
1.2 数据集的构建
实验的边坡土体深层水平位移值数据来源于四川升拓检测股份有限公司的SQLsever数据库,与之相关边坡工程项目为茂县石大关乡拴马村梯子槽滑坡监测项目。SQLsever数据库是美国Microsoft公司设计的一个为分布式服务器计算的、高性能的、可扩展的关系型数据库管理系统。
由于数据采集设备故障和外界环境等原因,导致了部分时间点的采集数据出现缺失。因此为降低预测误差,故选取监测数据值连续而稳定的时间段来进行预测实验。
随机选取监测项目中某个土体深层水平位移监测点的500~650个数据。之所以选500~650个有两个原因:一是如果数据取的太少就无法充分挖掘原序列中的信息,而选取数据过多又会因序列前后间隔太长,使前期数据与后期预测数据关联性变弱,而造成不必要的计算量;二是查阅诸多相关的时间序列预测文献,若对季度数据(m=4,按1年4个季度循环)实证分析的原始序列个数在50~100,月度数据(m=12,按1年12个月循环)的个数在250~350,因此对时度数据(m=24,按1天24小时循环)实证分析的原始序列个数可取在500~650。
最终选取从2018年8月15日0:00~2018年9月10日23:00的“X轴”方向的所有整点数据构成“H”数据集及序列{Ht},数据量为648,见图1。从图1中可以发现,“序列{Ht}是明显的有确定性趋势又有周期性的时间序列。
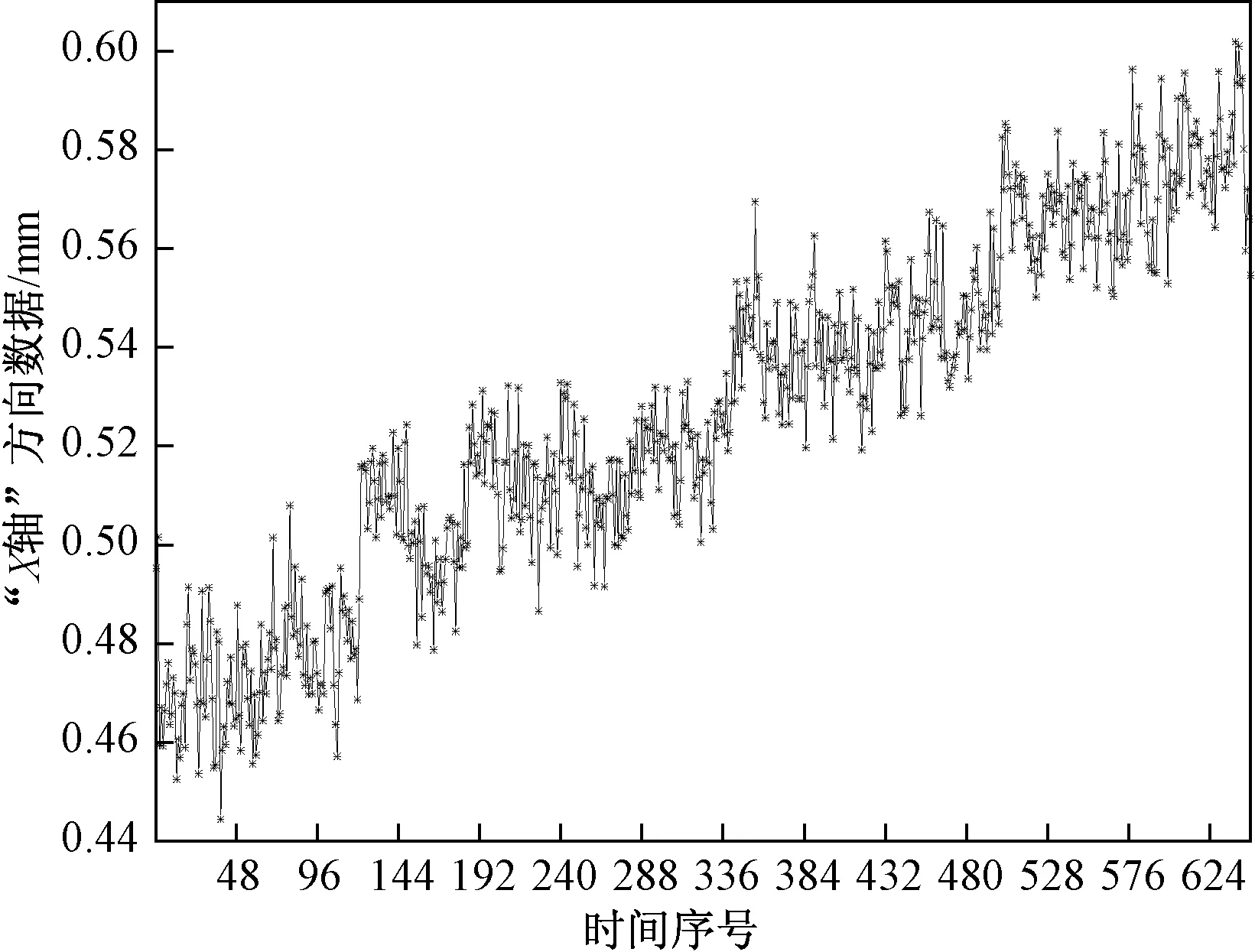
图1 “H”数据集的序列图Fig.1 The sequence diagram of the “H” dataset
2 ARIMA模型的建立与预测过程
2.1 模型的建立
设{Ht}为平稳时间序列且均值为零,则ARMA(1,1)的1阶自回归1阶滑动平均模型公式可表述为
Ht=φHt-1+et-θet-1
(1)
故ARMA(p,q)公式[14]表述为
Ht-φ1Ht-1-…-φpHt-p=et-θ1et-1-…-θqet-q
(2)
式(1)可简写为
φ(B)Ht=θ(B)et
(3)
式(3)中:et表示白噪声参数,t=1, 2, …,p;φ表示自回归系数;θ表示回归参数。在模型ARIMA(p,d,q)中,d代表差分阶数。因为边坡监测项目中,土体深层水平位移的时间序列数据普遍都是不平稳的,使序列平稳的途径有很多,差分就是其中之一,且ARIMA模型差分后的建模过程几乎与ARMA相同。
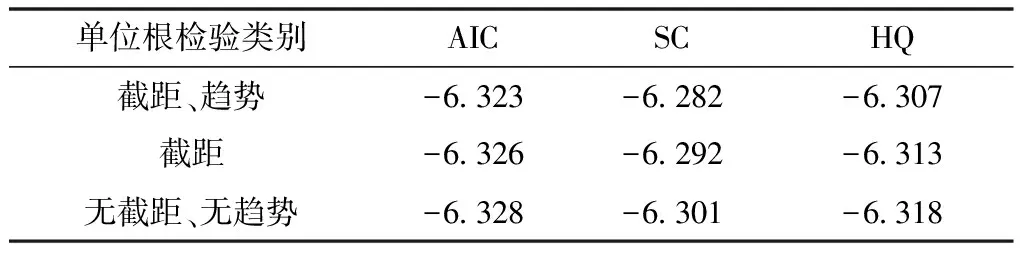
表1 一阶差分序列的单位根检验
注:AIC全称AIC信息准则,于1973年由日本统计学家赤池弘次提出,又称赤池(Akaike)信息准则[15]; SC指的是施瓦茨(Schwartz)准则,又称贝叶斯信息准则(BIC); HQ指的是汉南-奎因(Hannan-Quinn)准则[16]。
依据上述“三准则”,AIC、SC、HQ小的较优,则由表1的单位根检验结果,判断该序列为存在既无截距项又无趋势项的单位根过程。
由表2可以看出一阶差分的ADF检验的T统计值的绝对值为18.577 4,远大于显著性水平为0.05时的T统计值1.942,则存在一个单位根的原假设成立;其次P也很小。这均说明原序列的一阶差分序列是平稳的,因此d=1。
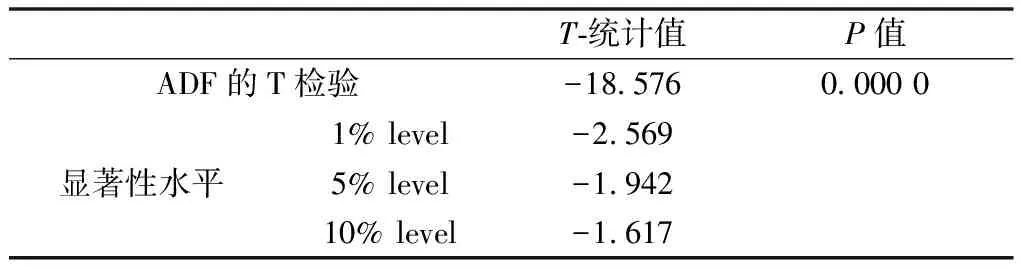
表2 一阶差分序列(无截距、无趋势)的ADF检验
从图2可以清晰地看到,DH的时序图围绕一个常数值上下波动,且波动区间不大;又从图3中可看出,自相关系数迅速衰减趋于0。综合所述,一阶差分后原序列是平稳的,不再进行二阶差分检验。
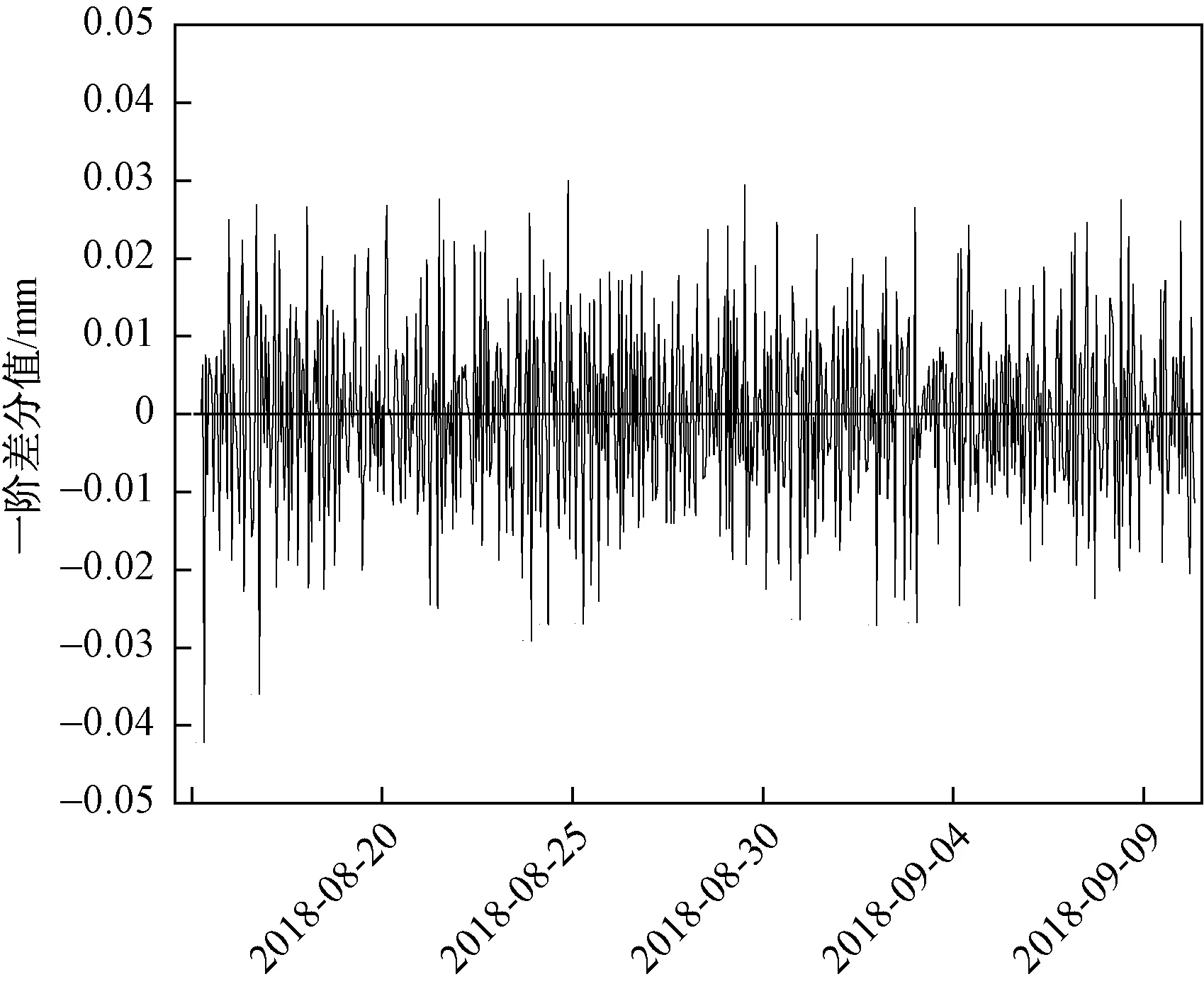
图2 “H”数据集的一阶差分时序图Fig.2 The first-order difference sequence diagram of the “H” dataset
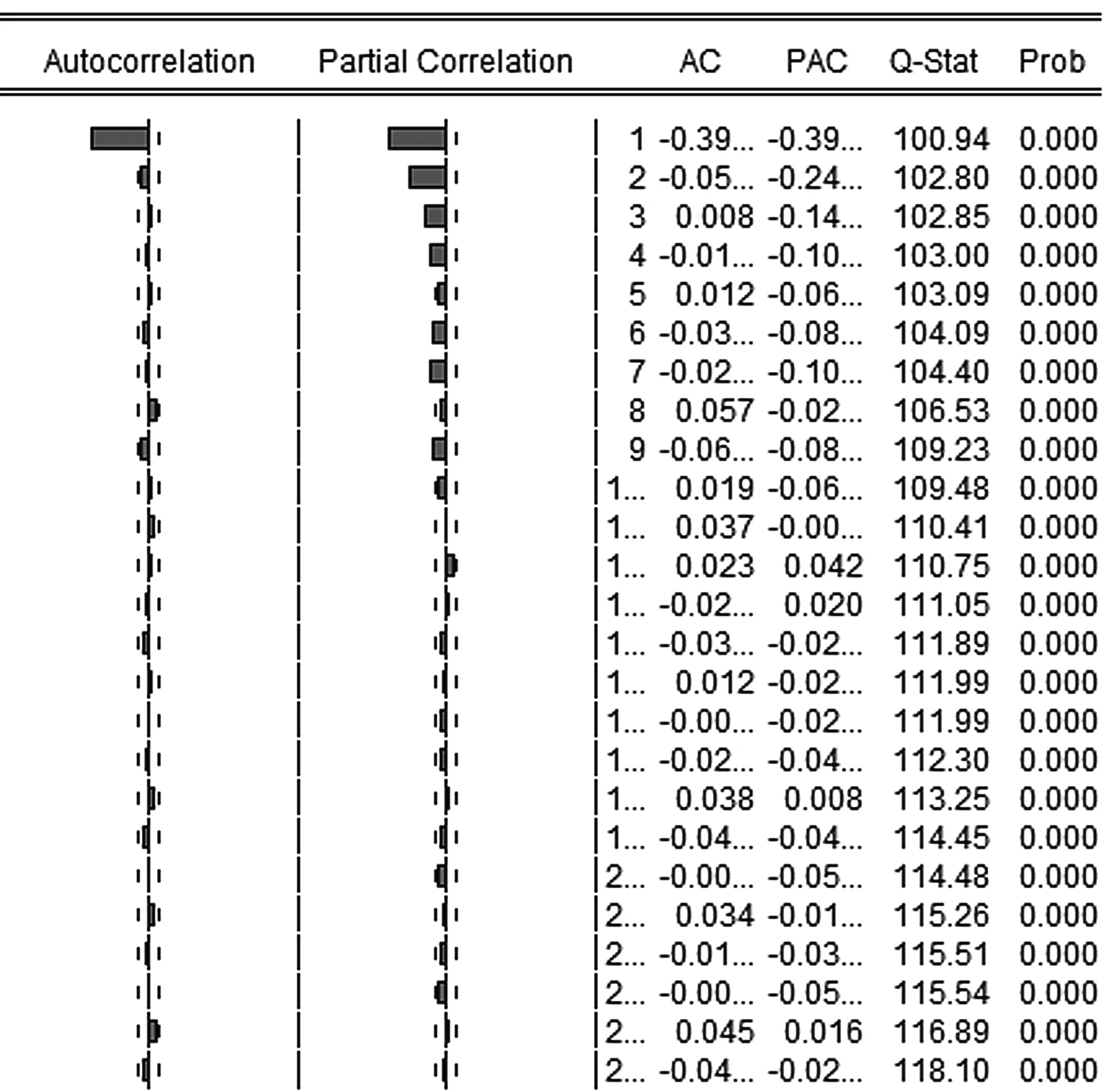
图3 一阶差分自相关图Fig.3 The first-order differential autocorrelation graph
从图3中可清晰地看到,P都小于0.05且接近于0,则原序列是非白噪声的,存在一定相关性,并有规律可循。在滞后阶数(lag)为4以后,偏自相关系数迅速趋近于0,初步判断一阶差分序列为偏自相关的4阶截尾,可试着拟合AR(4)模型;在lag=5时,偏自相关系数处于2倍标准差的置信带边缘,可尝试拟合AR(5)模型。而在lag=1时,自相关系数显著不为零,在lag=2、8时,它又处于2倍标准差的置信带边缘,则可试着去拟合MA(1)、MA(2)和MA(8)模型。因此可以初步拟合的模型有ARIMA(4,1,1)、ARIMA(5,1,1)等。最后由模型定阶发现,p可能等于4,q可能等于1、2、8,表3、表4分别是各个拟合模型的估计结果和预测参数对比情况。
依据P小于显著性水平0.05且越小结果越显著(模型较优)的判断原则,比较表3中c、ar(p)、ma(q)的P大小,综合得出ARIMA(3,1,1)模型最优。
先根据“三准则”,AIC、SC、HQ小的较优,对表4中各模型的检验统计量进行比较,得出ARIMA(3,1,1)有两项最小(SC、HQ);又依据F分布原则,F-statistics大的较优, ARIMA(3,1,1)的F统计量显然最大,P也小于显著性水平0.05。因此综合判断ARIMA(3,1,1)为最优拟合模型。
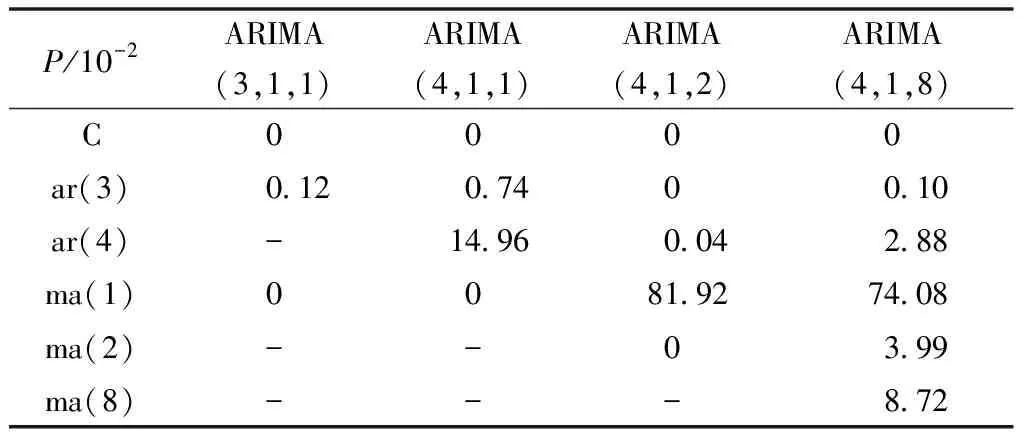
表3 方程的P比较
注:c表示常数;ar表示自回归过程,括号内表示滞后阶数;ma表示滑动平均过程,括号内表示滞后阶数。
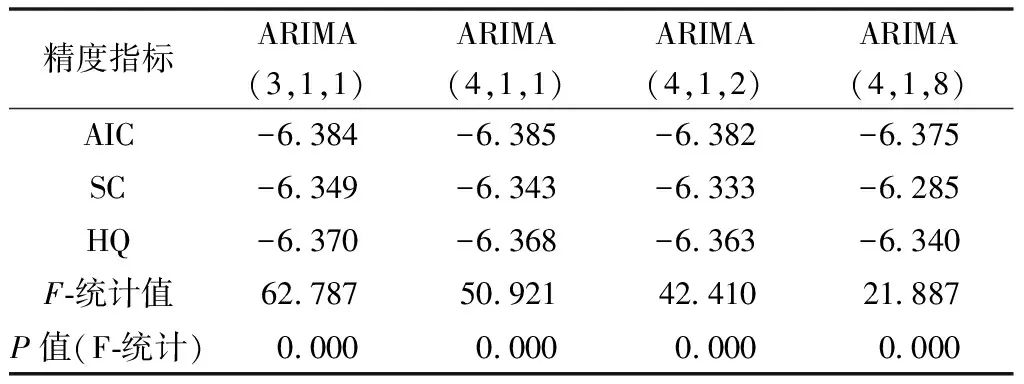
表4 各种模型的精度指标对比
模型ARIMA(3,1,1)的公式推导[9,14]如下:
因为:
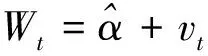
(4)
又:
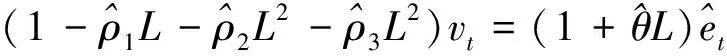
(5)
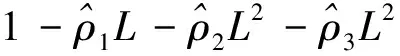
(6)
在式(1)两边同时乘以以(6)得:
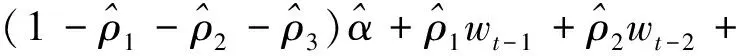
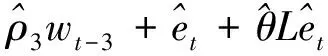
(7)
系数代入式(7)得出ARMA(3,1)模型的公式为
Wt=0.000 061+0.381 209wt-1+0.147 211wt-2+
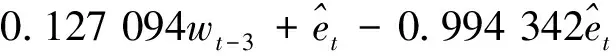
(8)
又令Wt=Ht-Ht-1,得ARIMA(3,1,1)模型的公式为
(Ht-Ht-1)+0.381 209(Ht-2-Ht-1)+
0.147 211(Ht-3-Ht-2)+0.127 094(Ht-4-
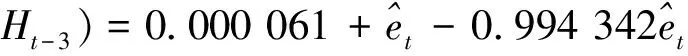
(9)
2.2 模型的诊断检验
在确定ARMA模型参数的估计值后,为了验证拟合模型的适应性,还需进行诊断检验。运用Eviews时间序列分析软件建立残差的自相关图,对残差进行纯随机性检验,图4是ARIMA(3,1,1)的残差自相关检验结果。
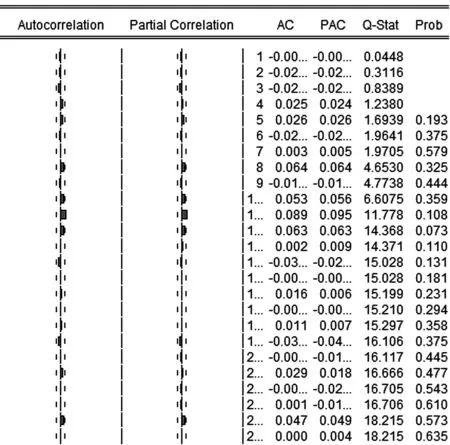
图4 ARMA(3,1,1)模型的残差相关图Fig.4 Residual correlation graph of the ARMA(3,1,1) model
从图4中可以看到,自相关函数值几乎都在0.95的置信区域内;其次,P都大于0.05,则表明残差为白噪声且是纯随机性的;又从ARIMA(3,1,1)模型拟合图(图5)中看出,拟合效果好。综合判断,拟合的ARIMA(3,1,1) 模型有效。
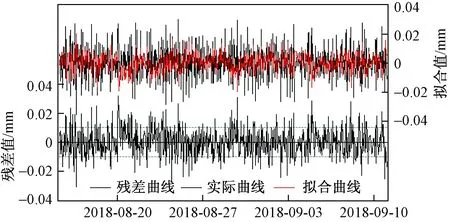
图5 ARMA(3,1,1)模型的拟合图Fig.5 The fitting graph of the ARMA(3,1,1) model
2.3 模型的应用
为验证拟合模型的适用性,现用模型ARIMA(3,1,1)进行预测,预测结果见图6,可以看出该模型的预测效果较理想。
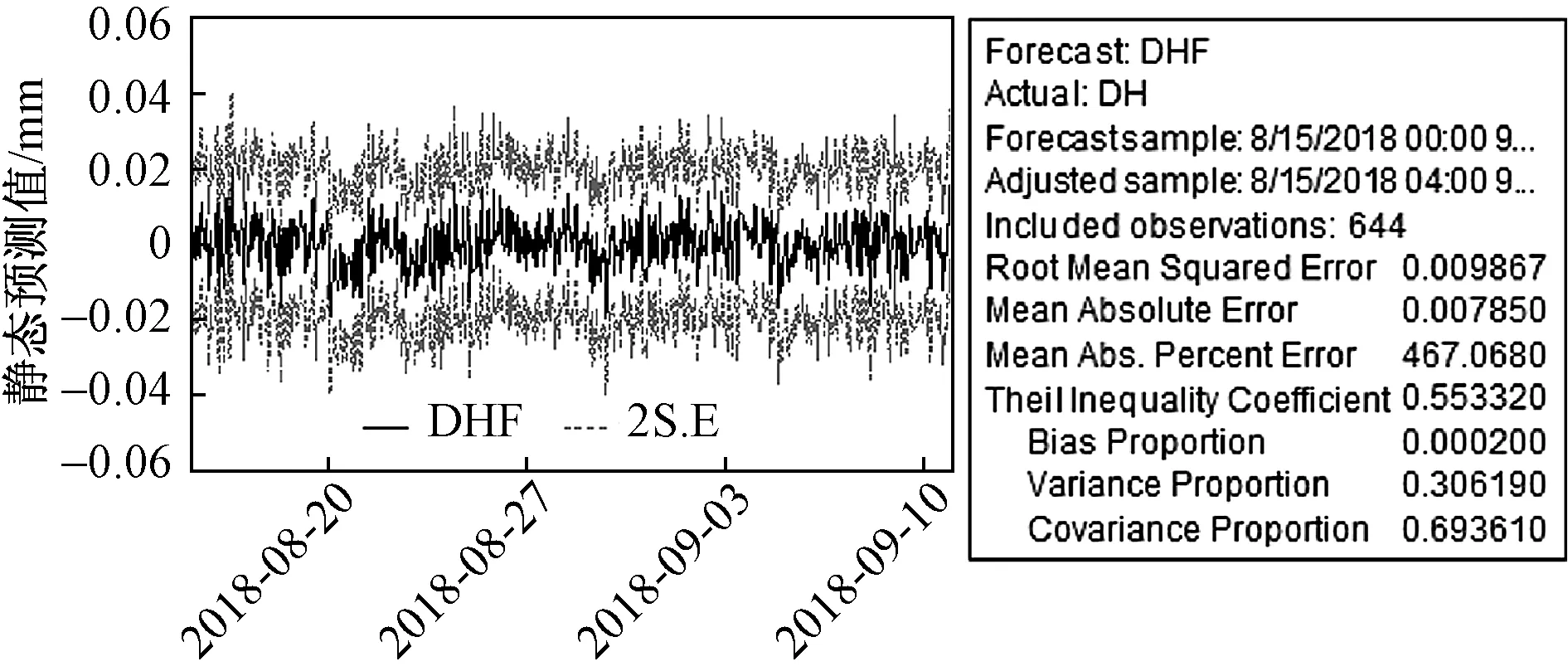
图6 序列静态预测图Fig.6 The sequence static forecasting graph
又将预测值存放在DH序列中,作出DH和DHF预测拟合图,见图7。从图7中可以看出,该模型的预测效果较好。
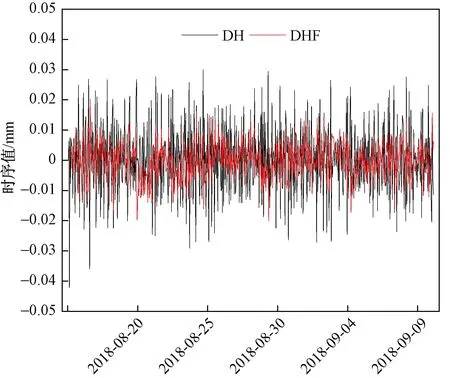
图7 静态预测拟合图Fig.7 The static forecasting fitting graph
现由在DHF中已有的预测值,利用模型ARIMA(3,1,1)的公式可反推出第一期预测值,又将预测值整合到原序列,同样的过程可得出第二期预测值,以此类推直到得出m(m=24)期,具体结果见表6。
3 基于阻尼模型的Holt-Winters方法预测
3.1 Holt-Winters预测方法
Holt-Winters预测方法的基本思想是把具有线性趋势、季节变动和随机波动的时间序列进行分析研究,并与指数平滑法结合,分别对长期趋势、趋势的增量和季节波动做出估计,然后建立预测模型,外推预测值[17]。Holt-Winters季节模型包含加法模型、乘法模型[18]。
Holt-Winters乘法模型的预测外推公式为
y′t+h=(at+hbt)st+h-m
(10)
a、b、s的计算公式如下:
at=α(yt/st-m)+(1-α)(at-1+bt-1)
(11)
bt=β(at-at-1)+(1-β)bt-1
(12)
st=γ[yt/(at-1-bt-1)]+(1-γ)st-m
(13)
为了预测更小时间周期的数据集,在乘法模型的基础上,添加延伸系数φ;再通过指数平滑法变换得到阻尼Holt-Winters模型的预测外推公式,如下:
y′t+h=[at+(φ+φ2+…+φh)bt]st+h-m
(14)
式中:a表示截距;b表示趋势;s表示阻尼模型的季节因子;t表示预测时间,且t=1,2,…,m;h表示平滑期数,h>0;m表示周期长度,例如,对于季度数据取4,月度数据取12。因实验数据间隔为小时,循环一次要24个采集数据,故取m=24。
a、b、s的计算公式如下:
at=α(yt/st-m)+(1-α)(at-1+φbt-1)
(15)
bt=β(at-at-1)+(1-β)φbt-1
(16)
st=γ[yt/(at-1-φbt-1)]+(1-γ)st-m
(17)
式中:α、β、γ为阻尼因子,也称平滑系数,在0~1之间取值。
3.2 可行性分析
为了检验数据进行预测研究的可行性,利用OriginPro,对“H”数据集进行离散分析,得到如图8的相邻时刻数据散点图。
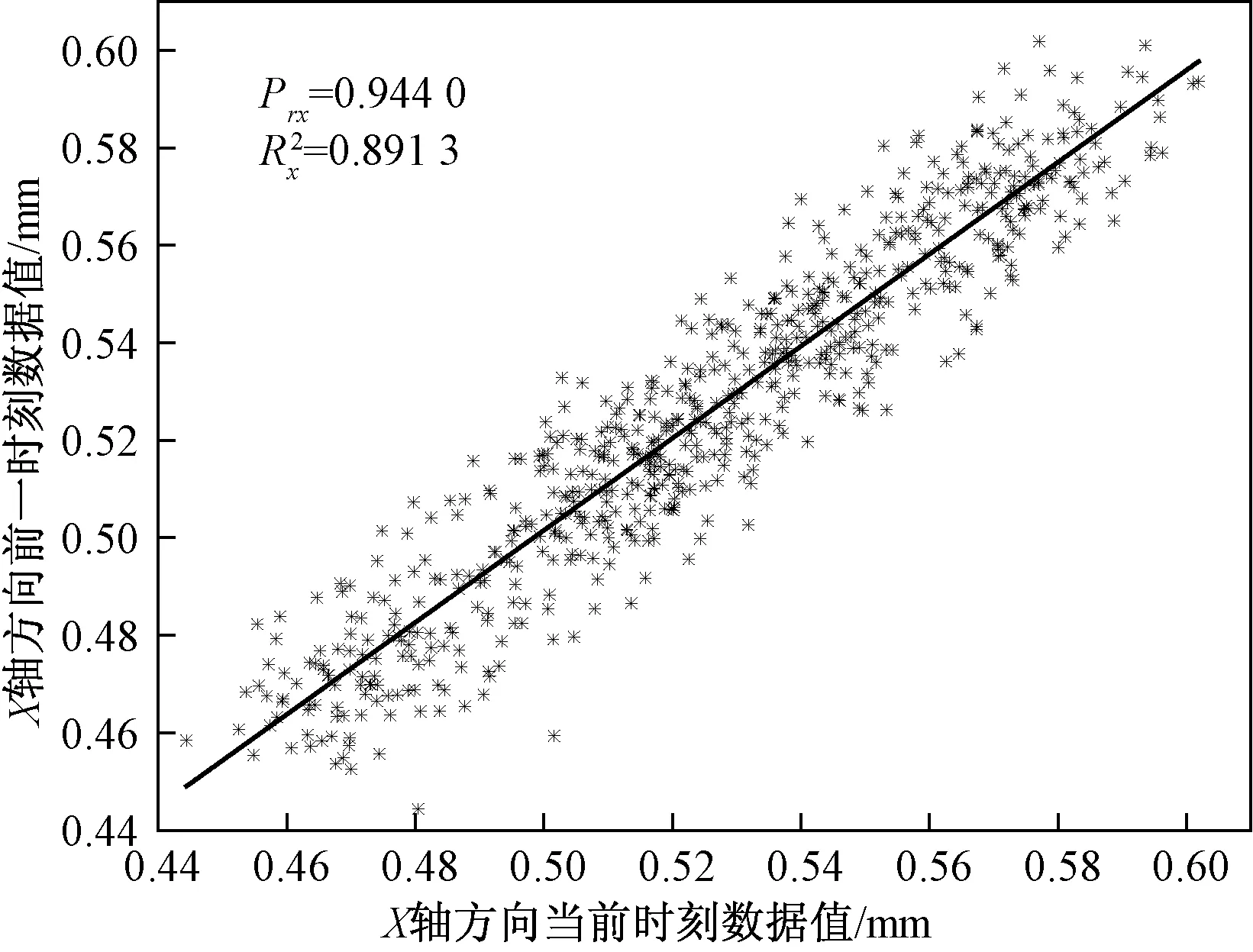
图8 “H”数据集的散点图Fig.8 The distribution point diagram of the “H” dataset
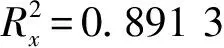
3.3 预测与结果分析
利用WEKA数据挖掘软件,让α、β、γ在[0,1]的区间内进行精度为小数点后两位的等值迭代运算,且预测误差=|实际值-预测值|/实际值×100%,得出:当α=0.03、β=0.03、γ=0.03时,“H”数据集的平均预测误差最小,为1.69%。
再分析平滑系数α、β、γ对预测误差的影响大小(α、β、γ的系统默认值都为0.2)。由表5可以发现,对于“H”数据集,当β为默认值时,平均预测误差变化最大,约为0.75%,因此推断改变β最有可能提高预测精度。

表5 平滑系数的影响分析
根据以上分析结果,对“H”数据集,拟定α、γ为不变量,β为变量,分析预测结果得出:当β=0.04时,最小预测误差约为1.68%,见图9。
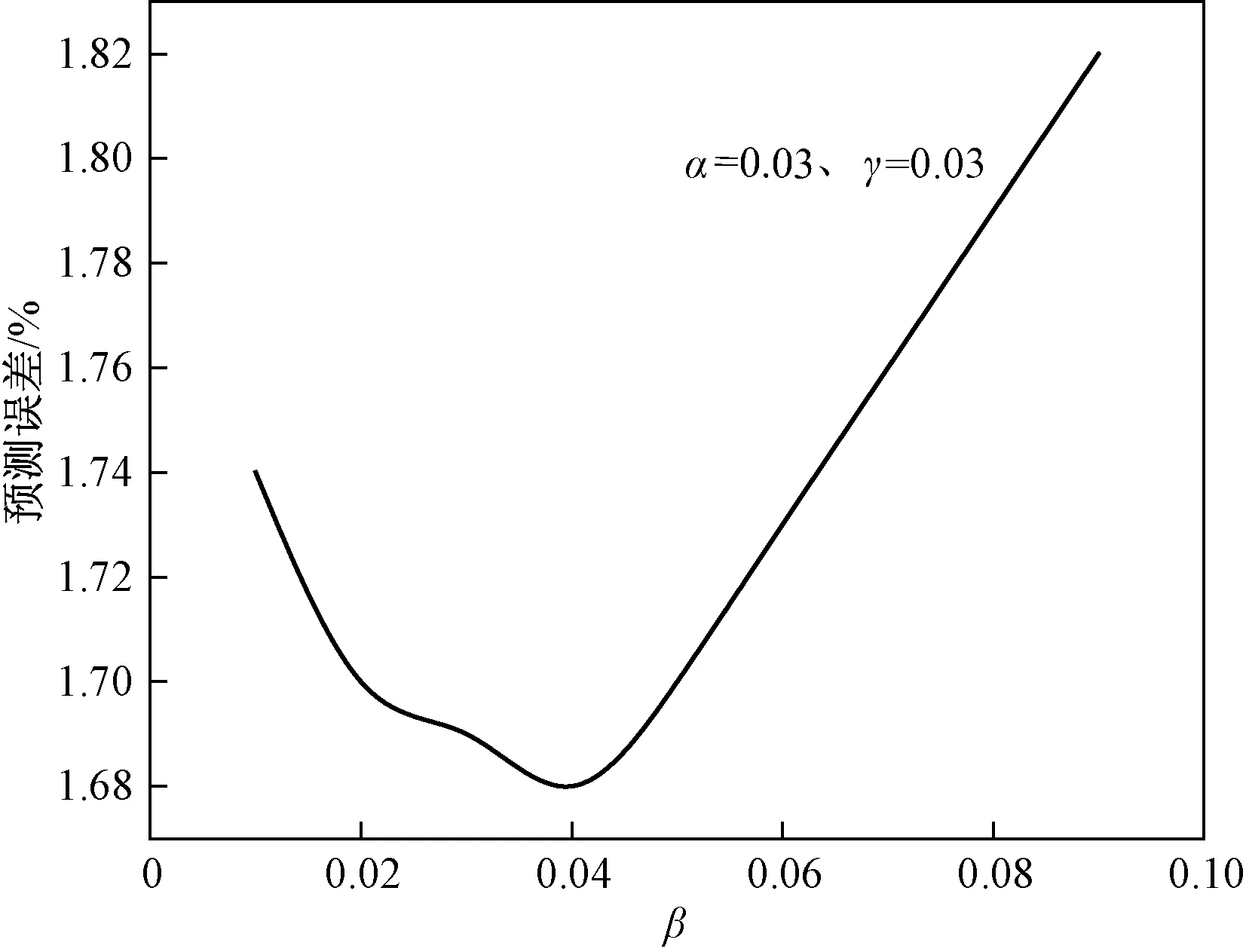
图9 “H”数据集的预测误差变化曲线Fig.9 The change curve in forecasting error of the “H” dataset
综上所述,当取α=0.02、β=0.03、γ=0.03时,“H”数据集的平均预测误差最小,为1.53%,具体预测结果见表6。
4 比较两种方法的预测结果
因为ARIMA模型和Holt-Winters方法对长期预测存在局限性,这里只给出24期真实值与预测值的比较情况,如表6所示。
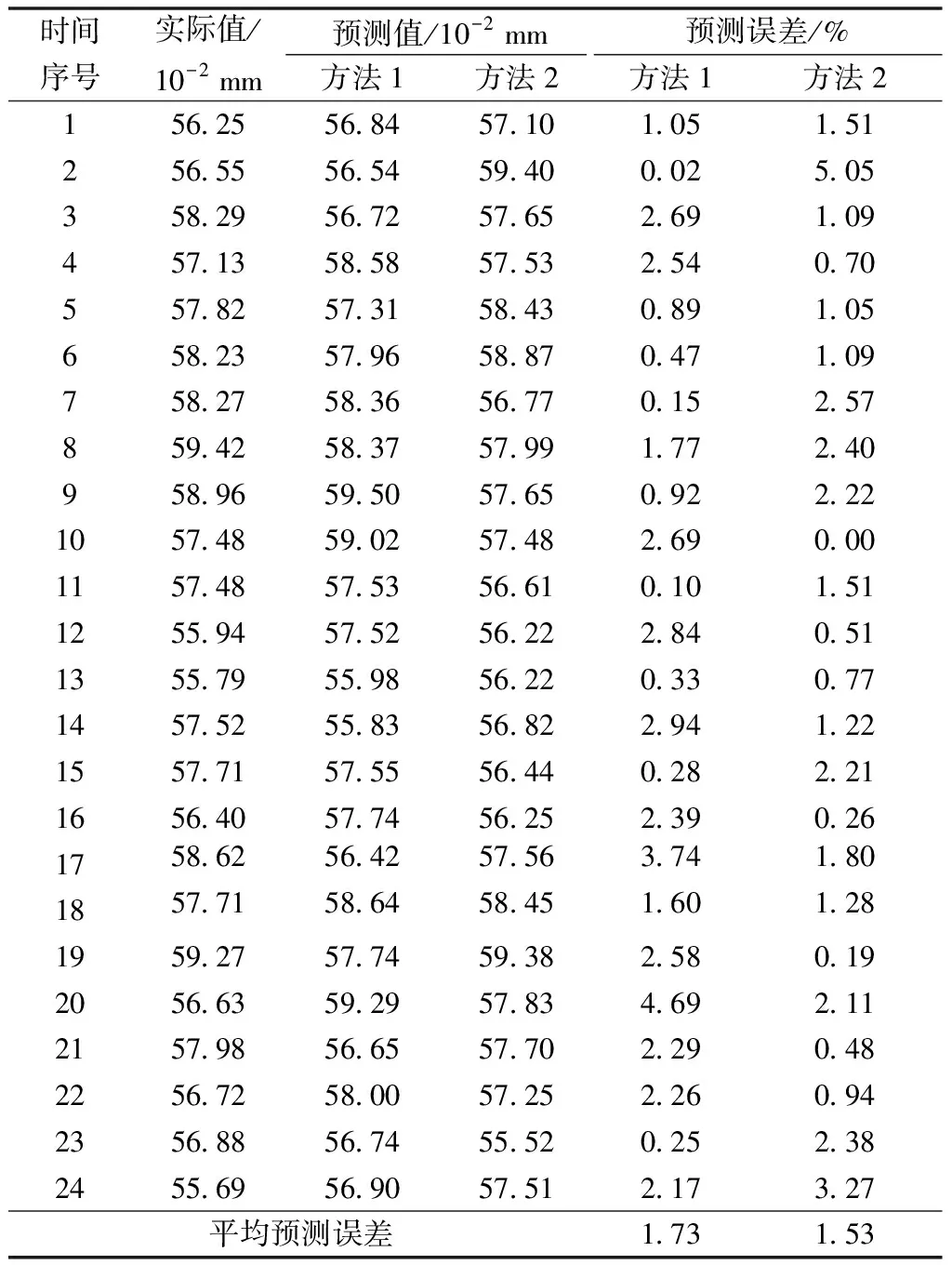
表6 两种方法的预测结果及误差
注:预测时间为“2018-09-11:00~2018-09-11:23”;方法1=ARIMA模型、方法2=Holt-Winters方法;预测误差=(|实际值-预测值|/实际值)×100%;实际值数据来源于四川升拓检测股份有限公司的SQLsever数据库。
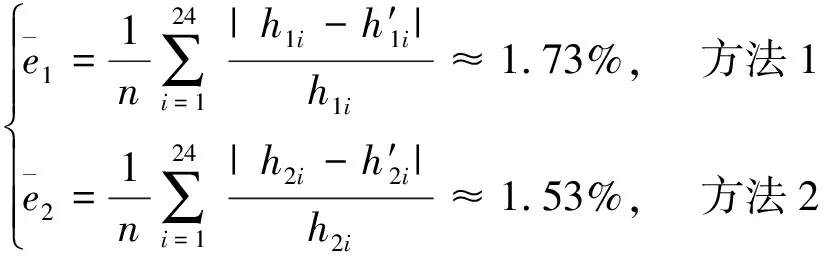
(18)
式(18)中:h1i和h′1i分别表示方法1的实际值和预测值;h2i和h′2i分别别表示方法2的实际值和预测值;i表示预测期数,i=1, 2, …, 24;n=24。
从表6可以看出,两种方法预测误差都偏小,且平均预测误差只有1.73%和1.53%;又从图11中不难看出两种方法的预测结果曲线与实际值曲线的变化趋势基本吻合;这都足以说明两种方法对“H”数据集的短期预测精度都很高。
现将两种方法的预测误差比较发现:虽然Holt-Winters方法的最大预测误差(5.05%)大于ARIMA模型(4.69%),但在总体上,ARIMA模型有11期预测误差大于2.22%,Holt-Winters方法只有5期,因此Holt-Winters方法短期预测效果更好,如图10所示。
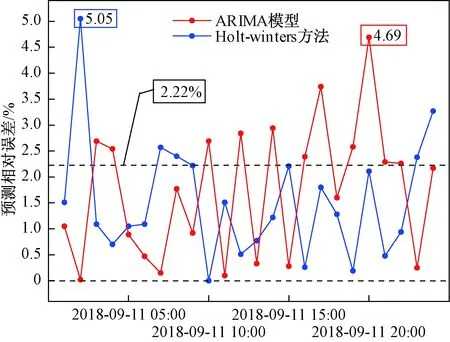
图10 比较两种方法的预测相对误差Fig.10 Comparing relative errors of the two methods
然而,根据实际值的95%置信度,计算预测区间,可以得到两种方法的预测曲线效果图,见图11。
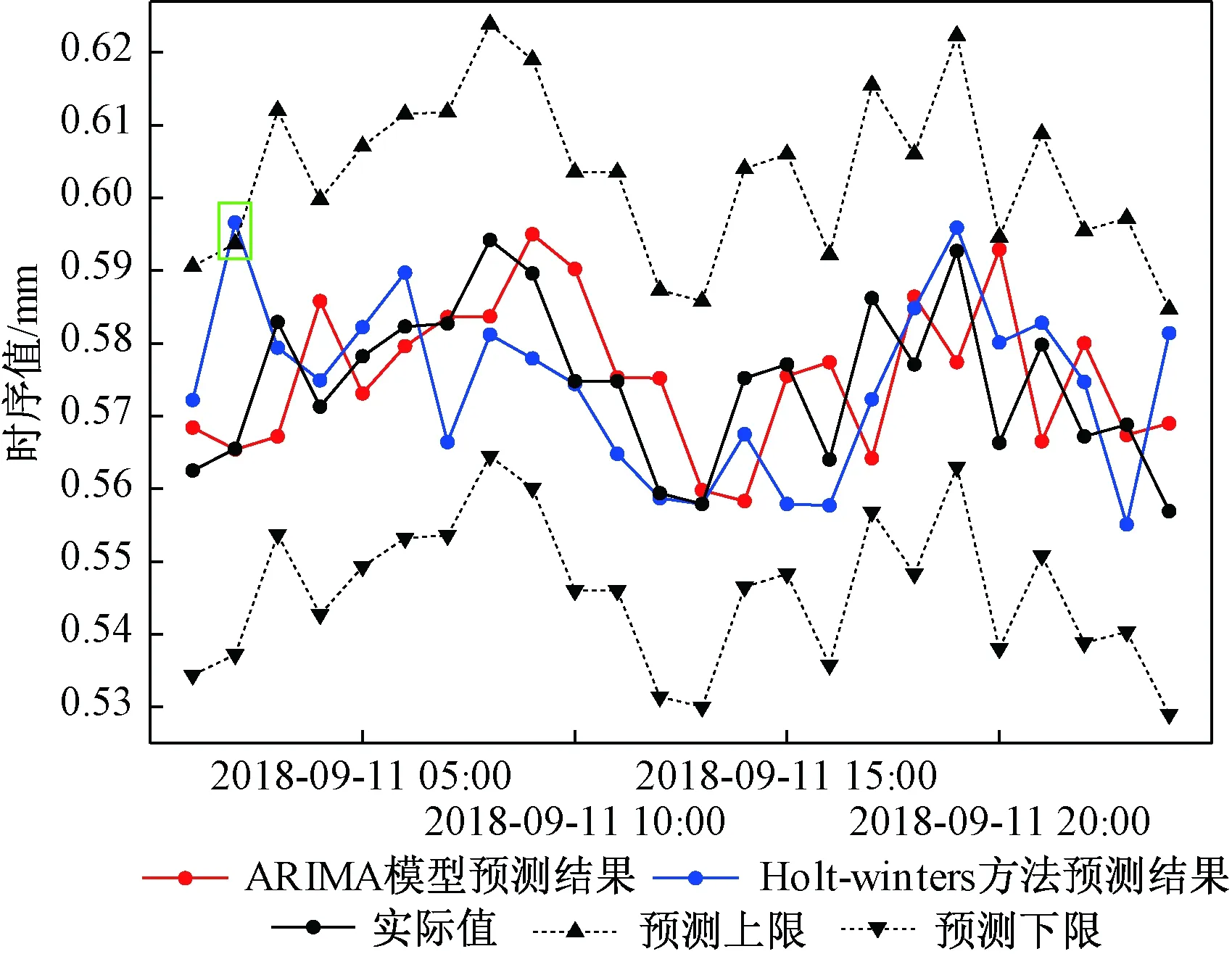
图11 两种方法的预测结果曲线Fig.11 The curvilinear in forecasting results of the two methods
在图11中,Holt-Winters方法尽管平均预测误差更小,但预测区间所包含真实值的概率小于ARIMA模型(图11中绿色矩形框标记的Holt-Winters方法预测点在预测区间外),因此ARIMA模型短期预测更稳定。
综上所述,对于土体深层水平位移的短期预测,两种方法各有特点。
5 结论
边坡土体深层水平位移预测是一个充满挑战性的问题,但时间序列预测一直被认为是对具有趋势性增长(降低)和时变性波动序列进行统计预测的有效手段。利用ARIMA模型和Holt-Winters方法对土体深层水平位移进行了预测,可以为边坡变形监测与预警提供一定的依据。
ARIMA模型和Holt-Winters模型都属于短期预测模型,随着时间的推移,它们的预测效果也会逐渐变差[19]。从两种方法的预测结果来看,短期预测效果都很好。其次通过分析其预测误差和结果曲线发现,两种方法各具特点:Holt-Winters方法的短期预测效果更好;ARIMA模型的短期预测结果更稳定。又从实际操作来讲,Holt-Winters方法简便,而ARIMA模型的建模过程较为烦琐,并且在p和q的选择存在很多评判标准。
总之,通过两种时间序列短期预测方法的比较研究,希望其结果对边坡治理人员加强边坡安全治理和预防边坡事故发生有帮助。另外也可考虑融合其他预测方法,加强对各种影响因素的关注,如边坡自身结构、天气变化、工程施工等,常常这些不稳定的因素对边坡土体深层水平位移的长期走势也有着重要的应用价值。

