坐标法整正曲线优化切线方向的探讨

廖显军

（中国铁路南宁局集团有限公司南昆铁路南百段增建二线工程建设指挥部，工程师，广西南宁）

1 前言

既有铁路曲线在经过长期运营后，其平面线形会逐渐发生变化，曲线的偏角、半径、缓和全长等要素与最初的设计值存在偏差，圆顺度差，为确保铁路运营安全，需要对曲线进行整正，将已变形的曲线恢复到标准曲线状态。

1.1 传统铁路曲线整正计算的基本要求 铁路曲线整正前后必须满足下列条件：

1）曲线转角值不变；

2）整正前后轨道长度保持不变；

3）坐标测量的起点和终点在曲线外的直线上，起点和终点的整正拨距为0，保证线路两端的位置是固定不变，以确定直线的方向不变［1］。

1.2 两端切线对曲线整正的影响 曲线要素中的偏角、半径、缓和曲线，任何一个曲线发生变化，都会对曲线平面形状产生影响，而切线方向的变化决定偏角的大小及线路平面位置。曲线整正为了达到整正最佳方案，整正过程中转角值是可以微调的，通过扭转两端切线方向来实现，因此传统铁路曲线整正要求整正前后必须满足曲线转角值不变的做法，存在一定的缺陷，所以有必要对坐标法整正进一步研究。

2 传统坐标法整正存在的问题

传统的坐标法整正计算，目前常用的优化方法是组合法，即以不同的缓和曲线l01、l02和半径R组合成多组组合，通过计算机辅助计算求出最优的拨道量。

通常是先在始、终端既有直线上任意分别取两点A、B和C、D求出两端直线方程，然后联立解方程求出交点坐标JD，将两端切线作为常量，优化两端缓和曲线l01、l02和半径R，共有3个变量。

传统坐标法整正曲线切线位置如图1所示：

图1 传统坐标法整正曲线切线位置图

结合图1介绍拨道量计算方法：在确定的切线方向条件下，优化出缓和曲线l01、l02和半径R后，沿设计线路中心线始点A至终D点范围内建立流动坐标系，以线路中心线上任意点为坐标原点，以该点的切线方向为横坐标轴，流动坐标系为X′-O′-Y′，如图1。各既有测点在流动坐标系中当横坐标值时，则认为该测点落在坐标纵轴上，对应的纵坐标Y值即为拨量，拨量方向：左转曲线，正值向外挑，反之向下压，，计算推导过程从略。曲线整正计算有多种计算方法，可参考相关书籍［2］了解。

实际上，既有线以离散的测点作为代表，并不是一线条，如图2所示。通过始、终端既有直线上任意分别取两测点A、B和C、D确定切线方向，这样两条切线方向组合对线路平面形状的影响都不一样。两端切线组合不同，产生不同的曲线转角大小，会影响到在确定的缓和曲线与半径条件下曲线的平面形状，当然也影响到设计曲线轨迹与既有线各测点的相对位置距离大小，拨量受影响很大。不同的切线组合优化出不同的曲线要素和整正拨量，由于传统坐标法整正未考虑将两端正切线作为变量参数进行整正，则必然遗漏许多整正方案，最终整正方案通常不是最佳的，所以必须将两端正切线作为变量参数进行整正，根据确定的拨量绝对值之和最小或拨量值平方和最小等作为目标函数，才能筛选出最佳的曲线整正方案。

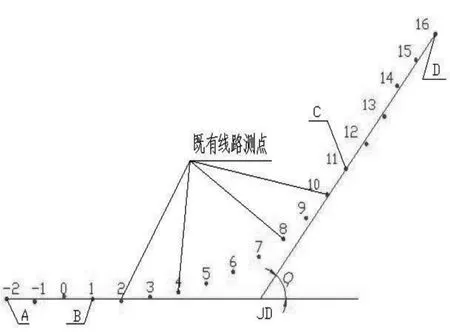
图2 传统坐标法整正曲线切线位置图

3 两端切线扭转参与曲线整正优化方法

笔者在结合工作实践感性体验和参考有关理论文献并做理性思考的基础上，着眼服务于现场提高工作效率和质量的需要，提出增加扭转曲线两端切线方向参与优化缓和曲线与半径的新方法。

本文所述新方法的要义是：由两端缓和曲线、切线和半径共5个变量参数整正曲线，主要内容简述如下：

如图3所示，在初步选定的始终端切线AB、CD的基础上，以最外端的A、D为固定点，以B、C点作为移动点在线路的法线方向上移动。在一定的移动范围内，B、C点以步长0.1mm从左至右移动，实现切线的扭转，按每扭转一步长，组合成一组切线，以缓和曲线长l01、l02和半径R或半径R为变量进行曲线优化。根据最佳目标函数，优化出每一组切线组合优化的缓和曲线长和半径，并对所有最佳目标函数进行筛选，找出最佳目标函数值对应的曲线要素，作为最终的曲线整正方案。

图3 切线扭转优化曲线要素示意图

4 算例

以某坐标法整正曲线为例，以拨量绝对值之和最小值作为目标函数优化曲线要素，将传统的固定两端切线方向整正曲线方法与扭转两端切线方向整正曲线方法作如下比较。

4.1 传统的固定两端切线方向整正曲线方法 根据传统的固定两端切线方向整正曲线方法，以第1（点A）、3（点B）、20（点C）和23（点D）号桩为始终切线4个固定点，第1、3、20和23号桩拨量均为 mm，整正计算拨道量如表1第8列所示。；

4.2 扭转两端切线方向整正曲线方法 扭转两端切线整正曲线新方法以第1、和23号桩为切线固定点，通过对第3号桩和20号桩进行扭转，第3、20号桩分别扭转-3.3 mm，2.3 mm，拨量分别为-3.3 mm，2.3 mm，第1和23号桩拨量均为0 mm，经过缓和曲线长、和半径，扭转两端切线整正曲线计算如表1第1～7列所示。

表1 扭转两端切线整正曲线计算表

根据传统的固定切坐标法和新的扭转两端切线坐标法整正结果比较如表2所示，目标函数为拨量绝对值之和最小，由表2可知，扭转两端切线方向整正的拨量绝对值之和为163.2 mm，小于固定切坐标法拨量绝对值之和196 mm，说明新方法整正曲线的质量优于传统方法。

表2 两种整正方法结果比较表

5 结语

通过对比传统的固定切线坐标法和新的扭转切线坐标法整正曲线成果质量比较，说明利用始终缓和曲线、始终切线与半径5个变量参数曲线整正质量优于传统的始终缓和曲线与半径3个变量参数，取得良好的整正效果，是对铁路坐标法整正曲线方法的有益改进。计算过程虽然复杂，但通过计算机辅助计算可快速求出最优的整正方案。

对于电气化铁路、铁路桥梁和重要建筑物等对控制拨量有诸多限制要求的曲线整正，此方法更能满足拨道量要求，如再通过修正曲线拨道量方式，曲线整正的方案能更好地适应现场拨道作业要求。