混流生产线作业指派的优化方法研究
王 克, 唐火红, 何其昌, 程 凯
(1.合肥工业大学 机械工程学院,安徽 合肥 230009; 2.上海交通大学 机械与动力工程学院,上海 200240)
0 引 言
混流生产是指多种产品在多条流水线上同时生产,它能够满足市场多样化与个性化的需求,是实际生产中普遍采用的一种实现方式[1]。生产实际中混流生产线常遇到生产作业指派不合理而导致的各条生产线上负荷不均衡、完工节点无法保证的问题,因此对混流生产线作业指派进行优化研究具有重要的应用价值。
指派问题的最经典算法是匈牙利算法,它主要适用于规模不大的平衡指派问题的求解;而对非平衡指派问题,虽然可以虚设任务或设备转化成平衡指派问题,但是在处理一些特殊数据时算法不能收敛,而且计算机上的编程实现比较困难,难以求解大规模任务指派问题[2]。除了匈牙利算法外,文献[3]将指派问题转化为一个能用对偶运输解法求解的容量运输问题,但该方法不够直观和简便[4]。文献[5]提出了一种树算法,该算法是一种简化的枚举方法,求解大规模任务指派问题较为复杂。
上述算法均是求解指派问题最优解的方法,不适合大规模任务指派问题的求解。近年来流行起来的启发式算法求解多约束的大规模任务指派问题效果较好,虽然得到的解可能只是近优解,但足以解决问题。
文献[6]使用了改进的粒子群算法,该算法复杂度较大;文献[7]使用了改进的自适应遗传算法;文献[8-9]使用了改进的蚁群算法,这些算法中某些参数选取需要大量试验才能确定。文献[10]使用了全局搜索算法,但仅适用于解决设备比任务多且一任务对一设备的情形。
本文是在模拟退火算法的基础上对其进行改进,通过指定优化方向以降低迭代次数,并综合遗传算法来弥补全局搜索能力。以某变压器横剪线为例,在Delmia/QUEST软件平台上参数化建立该物流仿真模型,并通过与实际生产进行对比确保该模型的精确性。对原始人工方案与本文方法优化的方案进行仿真实验,通过2种方案机器平均利用率与生产周期的比较,验证了本文方法的有效性和可行性。
1 问题的数学模型
1.1 问题描述与分析
考虑一个具有m个机器、l个相互独立的作业任务的混流生产线指派模型,如图1所示。其中Mi表示机器;Bi为缓存区;J1,J2,…,Jk,…,Jl表示顺序加工的作业序列,每个作业可以分配到多个设备,每个设备可以分配多个作业。这批作业如何分配能实现作业完工时间最短是本文研究的主要问题。

图1 混流生产线模型
在实际中,该问题受到每个作业的计划工作周期、设备加工能力、作业元素间的组合、缓存空间约束等条件的约束,其数学模型很难用确切的函数式表示。因此,对问题进行简化并作出如下假设:
(1) 每个机器开始加工这批作业的开始时间是确定的。以所有机器中最早开始作业时间为时间零点,设Mi的初始时间补偿值为STi,其表示时间零点到机器Mi的开始作业时间之间的工作时间。
(2) 作业可以划分成一些作业元,作业元是相互独立的、必须指派到同一个机器的、最大的作业元素集合。设作业任务Jk划分为lk个作业元,即Jk={Jk1,Jk2,…,Jkj,…,Jklk},又设这批作业共划分了n个作业元,令J′表示转化后的作业元序列,即J′={J11,…,J1l1,J21,…,J2l2,…,Jj1,…,Jjlj,…,Jl1,…,Jlll},又记为J′={J1′,J2′,…,Jj′,…,Jn′}。
(3) 每个机器上物料都及时供应,在加工这批作业时机器100%利用。设工艺时间矩阵为TC,设TC=(tij)m×n,其中工时变量tij表示作业元Jj′在机器Mi上加工的工艺时间。
(4) 缓存空间足够大且机器不会发生故障、插单等随机事件,不会影响机器的正常加工。
基于上述假设,该问题的约束只剩下设备的加工能力约束与任务时间约束,而且任一作业任务的完工周期也易于得出,该指派问题约束的数学表达式也能够表示。除此之外,指派问题模式也转变为每一作业元只能分配给1个机器,1个机器可以分配多个作业元,该指派问题的数学模型也易于表示。
为了表示作业元指派结果,引入0-1型决策矩阵X,其中X=(xij)m×n。
当决策变量xij=1时表示作业元素Jj′指派给机器Mi;当xij=0时表示作业元素Jj′没有指派给机器Mi。
当对于设备加工能力约束的数学描述,采用一个m×n的0-1型设备约束矩阵,记为M=(mij)m×n,其中,当mij=1时,表示设备Mi上能够加工作业元Jj′;当mij=0时,表示设备Mi上不能够加工作业元Jj′。
假设表示这批作业序列J1,J2,…,Jk,…,Jl的计划生产周期向量为Tp,即Tp=[T1T2…Tk…Tl],其中任一Tk为时间零点到Jk的完工节点之间的工作时间。则作业的计划工作周期约束的数学表达式为一个STi、TC与Tp的不等关系式。
1.2 混流生产线作业指派数学模型
混流生产线作业指派的数学模型如下:
(1)
s.t.

(2)
xij≤mij
(3)
k=1,2,…,l
(4)
xij=0或1
(5)
mij=0或1
(6)
其中,(1)式中T为所有作业实际生产周期,也就是该问题的优化目标;(2)式表示一作业元只能分配给1个机器;(3)式表示设备加工能力约束;(4)式表示作业的计划工作周期约束,其中Lk为前k个作业划分的作业元的总数目。
2 作业指派优化算法
2.1 模拟退火算法概述
模拟退火算法是受到固体退火过程的启示发展起来的一种随机寻优算法。该算法存在2个循环,即内循环与外循环。
内循环是在同一温度下按照一定的原则进行随机搜索并筛选出更优或可能更优的解。其实现过程是通过新解产生机制产生1个新解,并由新解接受原则判定新解是否接受,接受就继续迭代,不接受就重新产生新解。新解接受原则一般采用Metropolis准则,较优的解会被接受,较差的解有一定概率会被接受以防止陷入局部最优,并且随着温度的下降该概率会逐渐减小。外循环是温度的下降的迭代过程,在温度下降的过程中,解逐渐收敛。
模拟退火算法具有很强的局部搜索能力,是解决作业指派问题的有效方法之一,但也存在全局搜索能力差、收敛速度慢等缺点。
2.2 模拟退火算法的改进
由于遗传算法具有良好的全局搜索能力,将模拟退火算法与遗传算法相结合,对群体中个体采用模拟退火算法寻优,整个群体使用群体算法寻优,以改进算法的全局搜索能力。
但是上述改进同样会增加算法的复杂度,使算法的收敛速度变慢,鉴于此,将模拟退火算法的随机寻优指定优化范围。对于作业指派的问题,将优化目标定为所有作业的最小完工时间,显然目标函数值仅仅由作业最后完工机器的分配任务量确定。若将该机器上的任务分出一部分可分配任务匀给其他机器,则有很大概率会降低完工时间。因此将作业最后完工机器看做瓶颈,将作业任务分配的优化范围限定为分配到瓶颈机器上的作业元。
2.2.1 适应度函数
为了简化运算,采用罚函数的方法解除约束条件(4),设计出的适应度函数如下:
f=Cmax-(ω1T+ω2TD)
(7)
其中
(8)
(9)
(7)式中ω1与ω2是权重,有ω1+ω2=1。ω2值影响着完工时间节点的约束力度,当给定ω2一个初解,若通过该算法得到的结果不能满足完工时间节点的约束(即TD>0),则需适当增加ω2的值,重新进行优化。
(8)式中Cmax是一个不小于最大可能周期的值,以保证适应度为正值。
(9)式表示平均每项作业的延迟时间,其中ΔTi为第i个作业的实际工作周期与计划工作周期的差值。
2.2.2 算法编码
考虑到约束条件(2),则算法的编码方式如图2所示。
编码的前n位确定了分配方案,即解X。最后一位表示瓶颈机器,它是在计算实际生产周期时取得最大周期的机器。其中解X与前n位编码的转换公式为:
(10)
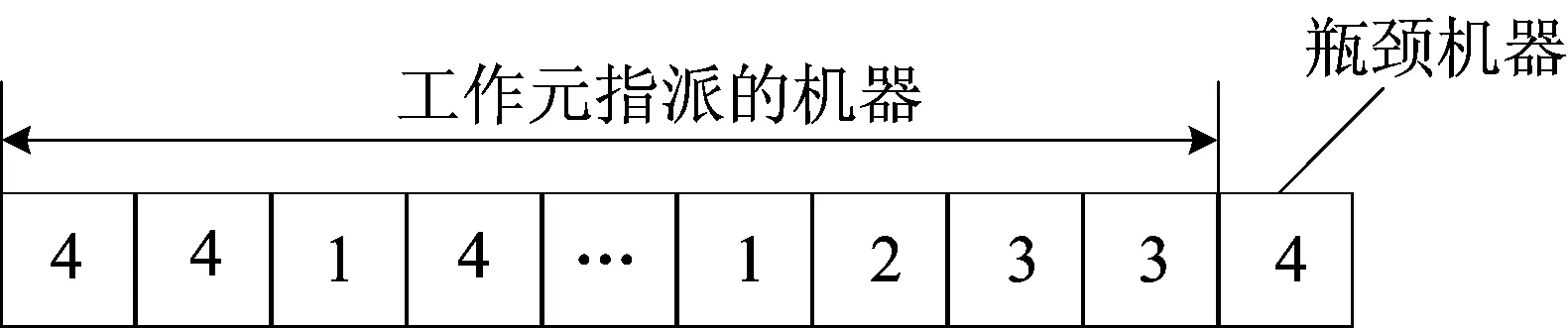
图2 算法编码
2.2.3 编码生成机制
由于作业元受到设备加工能力的约束,编码生成时需要排除不能加工的机器。一般地,该编码产生机制是随机产生一个在闭区间[1,m]之间的整数,而考虑到约束条件(3),则编码生成机制如图3所示。
2.2.4 新解产生机制与接受原则
个体新解的产生机制采用指向瓶颈机器的编码变异方法。实现方式是在解X的瓶颈机器所在行中,采用类似编码生成机制的方法,随机选出一个指向瓶颈机器的编码位,重新生成该位的编码。
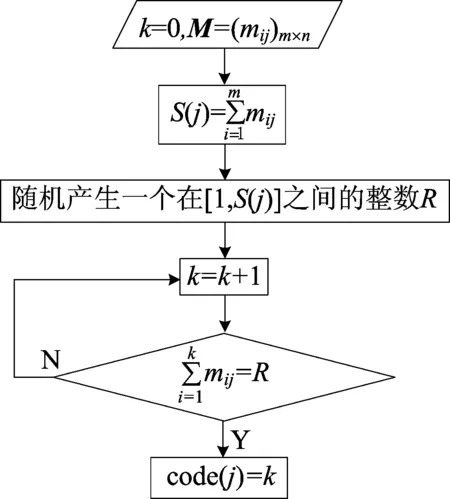
图3 编码生成机制
新解的接受原则采用Metropolis准则,其新解接受概率为:
(11)
其中,t为当前温度。
2.3 作业指派优化算法流程
对于研究的作业指派问题,本文结合遗产算法的群体寻优与模拟退火算法的个体寻优,提出了一种优化算法,该算法流程如图4所示。

图4 作业指派优化算法流程
其中选择操作采用轮盘赌机制,交叉操作使用单点交叉的方式。
遗传算法的变异操作被替换为模拟退火的操作,其中冷却进度表的参数如下:
(12)
(13)

(14)
3 实例仿真分析
以某变压器生产企业横剪车间为例,该企业主要生产超高压变压器,生产变压器的种类有上百种,横剪车间平均每天加工100多吨的任务。横剪车间主要任务是剪切出变压器铁芯需求的铁芯片。
变压器铁芯一般由轭、边柱、中柱组成,每一部分都由一些片型组成,这些片型中有一部分可以组合加工,为了方便叠装一种片型,或组合片型必须由一台横剪线加工,这些片型或组合片型即为作业元。
已知该企业4台横剪线均不同,其加工范围主要受到片型型号及片型最大宽度的约束。每台变压器都由一个工号标定,变压器的横剪任务在其工号的横剪套裁表中。横剪套裁表包括变压器铁芯需求的一系列片型表单,每个片型表单中含有所有片型等级及其铁芯片长度、宽度、数量、片厚、硅钢片牌号、设计重量等,由每种片型表单及横剪线速度即可测算出每种作业片型的理论加工时间。以某月的横剪任务为例进行仿真,该月横剪任务内含有192个作业元,分配到4台横剪设备,这些机器同时开工。
取种群规模为30,交叉概率为0.8,ω1、ω2分别为0.8、0.2,种群终止在500代,利用Matlab编程实现上述算法,得到优化解,结果发现得到的结果中部分作业超出了完工节点,TD>0,因此将ω1、ω2分别取0.7、0.3重新仿真,仿真结果中所有作业都在完工节点以内。该作业指派算法的优化进程如图5所示。
为了验证算法的有效性,在Delmia/QUEST中建立横剪车间的物流模型,分别对遗传算法、模拟退火算法以及本文混合算法得到的分配方案与原始人工分配方案进行仿真,对比结果见表1所列。
从表1可以看出,本文算法和优化方案相比于原始方案有了较大改善,也比遗传算法和模拟退火算法得到的解更优,证明了本文算法的有效性和优越性。
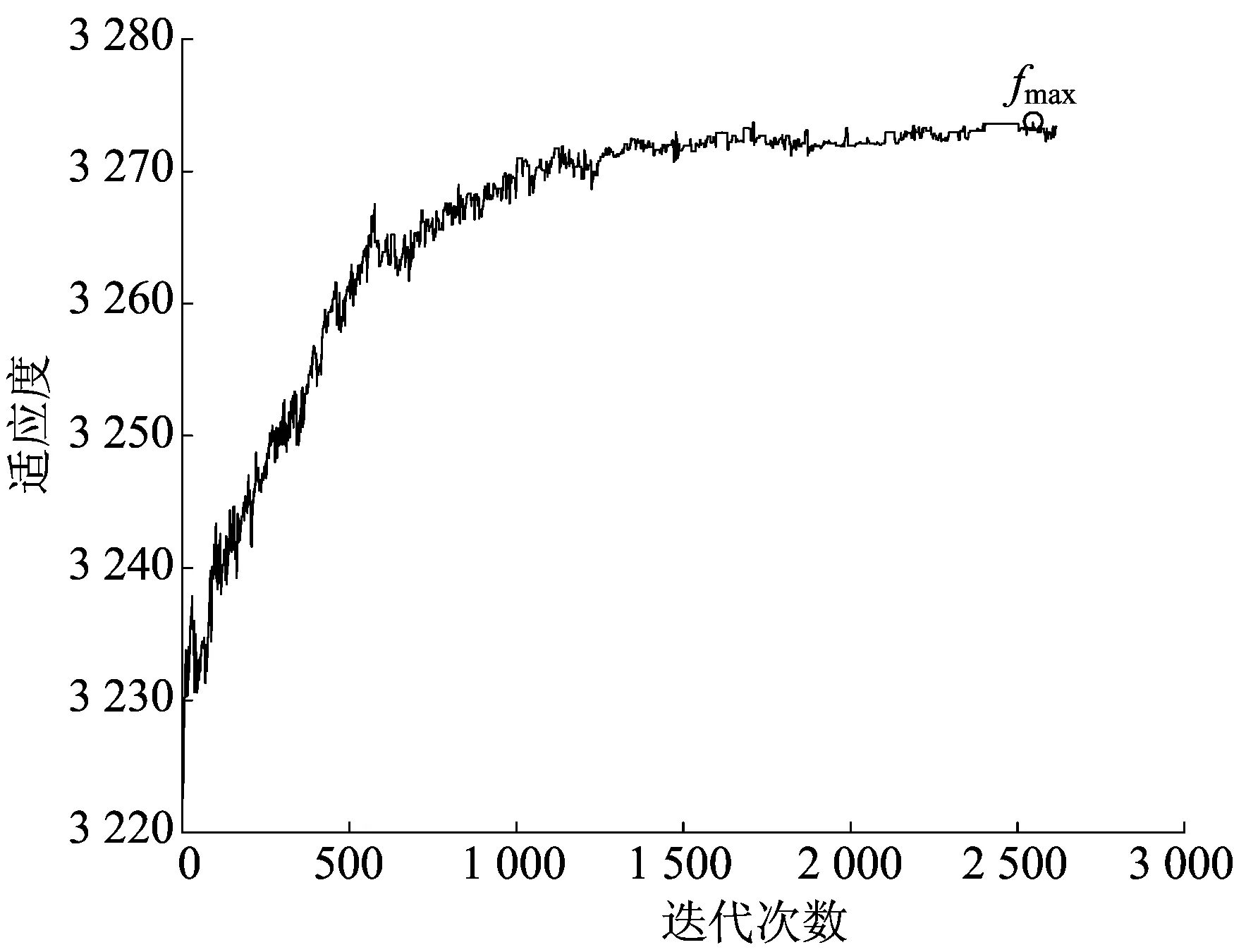
图5 作业指派优化算法优化进程
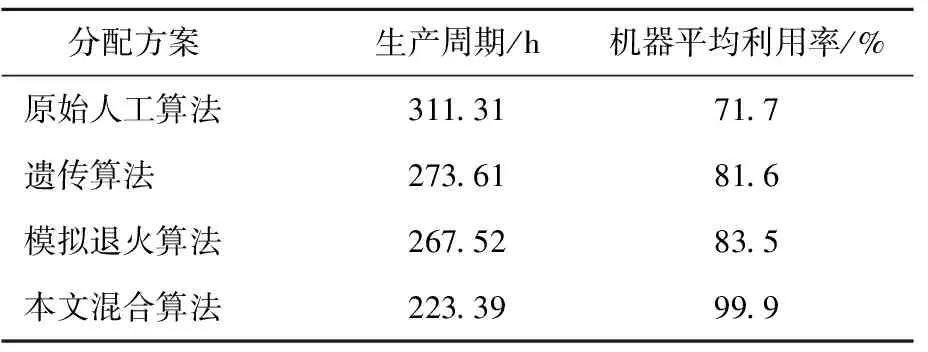
表1 算法优化方案与原始方案对比
4 结 论
本文采用一种混合遗传算法与模拟退火算法的优化方法来解决作业指派的问题。问题的目标函数是最小作业完工时间,考虑任务时间约束与设备能力约束,种群整体寻优与个体指向瓶颈机器寻优相结合,保证解的精确性。基于Delmia/QUEST的物流仿真对于算法优化结果起到了辅助验证的作用。实例结果表明了该算法可以使作业指派更加平衡,缩短了生产周期,提高了设备利用率。

