组态相互作用对Gd离子谱线分布的影响

杨李，何俊，吴涛

(武汉工程大学光电信息与能源工程学院，湖北 武汉 430205)

0 引言

极紫外光刻技术是制造特征尺寸小于22 nm集成电路芯片的一项重要技术[1]，随着科学技术的迅猛发展，人们在半导体工业制造中，希望在更小尺寸上集成更多的电子元件来实现设备的更多功能，因此科学工作者把目光投放在亚10 nm的极紫外光刻光源的研究上[2].根据目前制备极紫外多层膜的技术水平，La/B4C多层膜在6.xnm反射率可达46.2%[3]，因此亚10 nm的极紫外光刻光源的研究集中在6.xnm波长处.研究结果表明，到目前为止，稀土元素钆(Gd)是极紫外光源中转换率最高的靶材[4]，该靶激光等离子体光源是亚10 nm的极紫外光刻光源最有潜力的竞争者之一.

近年来，全球已经有多个研究团队着手这方面的研究工作.爱尔兰都柏林大学的Otsuka T等人研究计算结果表明，Gd离子在6.7 nm附近有密集的原子跃迁线列阵[5].O’Sullivan G等人通过理论计算研究证明，钆靶等离子体光源在适当的等离子条件下可在6.7 nm处0.6%的光谱宽带内获得0.4%的转换效率[6].Carrol P K等通过对原子序数在62 ～ 74之间的稀土元素的发射光谱进行研究，表明Gd17+—Gd25+离子在6.5 ～ 6.7 nm附近发生跃迁可产生强窄带辐射[7].因此，在转换效率最高且在6.7 nm附近能产生较强的光谱跃迁列阵的优势下，钆离子是更有研究价值的亚极紫外光刻光源.D Kilbane等人用Flexible Atomic Code(FAC)在不同的等离子体参数条件下，对钆离子极紫外发射光谱进行了模拟[8-9].本文中我们运用Cowan程序[10]对原子数据进行计算，得到Gd离子在19价到25价所产生的4p-4d和4d-4f的跃迁光谱，并着重分析组态相互作用对谱线分布的影响.

1 理论方法

1.1 中心场近似下哈密顿算符的计算Cowan代码是由Robert D Cowan开发的基于多组态相互作用的原子结构和光谱计算程序包[11-12].通过Hartree-Fock(HF)方程[13]计算电子径向波函数，单电子的哈密顿算符()如下：

(1)

对于单电子径向波函数Pi(r)，组态的平均能量由下式表示：

(2)

(3)

(4)

ck是标准化的球面谐波函数，而FK和GK可以用斯莱特[13]积分RK表示：

FK(ij)=RK(ij,ij)

(5)

GK(ij)=RK(ij,ji)

(6)

(7)

对(5)、(6)和(7)方程进行迭代求解，可以得到所求波函数.

1.2 Cowan code理论方法Cowan程序由4个子程序组成，分别为RCN、RCN2、RCG和RCE，在计算过程中只用到RCN、RCN2、RCG.RCN是用Hartree—Fork(HF)方法计算电子径向波函数Pnili=Pi,

(8)

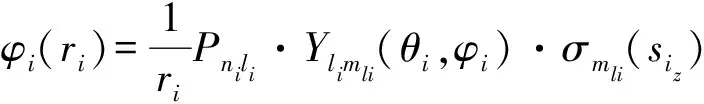
(9)

反对称波函数基组是由N电子体系单组态构成并表示为

ψ=(N!)-1/2∑(-1)Pφ1(rj1)φ2(rj2)φ3(rj3)…φN(rjN)

(10)

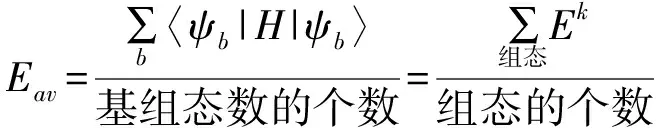
(11)

ψb是该组态的一个基组，Ek是Hamilton量的本征值.在单电子近似下Hamilton算符为：

(12)

该算符中包含电子动能项、电子与原子核相互作用项、自旋轨道相互作用项和电子与电子之间相互作用项.利用(10)式中构建的非耦合基组可将组态平均能改写为

(13)

(14)

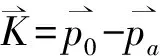
2 结果与讨论

2.1 组态平均能随电离度的变化为定性分析谱线分布范围和组态相互作用强弱，首先计算钆离子在不同离化度下，下列电子组态4p54dn+1、4p64dn-14f、4p64dn-15f、4p64dn-15p和4p64dn(n=3～10)的组态平均能，组态平均能随电离态的变化如图1所示.计算得出随着离化度增大组态平均能增加的是4p64dn-15p、4p64dn-15f和4p64dn-14f，因此随着离化度增加，4p64dn-15p、4p64dn-14f和4p64dn-15f组态跃迁产生的谱线波长分布向短波方向移动，只有4p54dn-1是减小的，4p64dn组态跃迁产生的谱线波长，向长波方向移动.从图1中可以看出，4p64dn-14f和4p54dn+1的组态平均能非常接近并出现交叉，在一定程度上反映出这两组态间存在较强的组态相互作用.

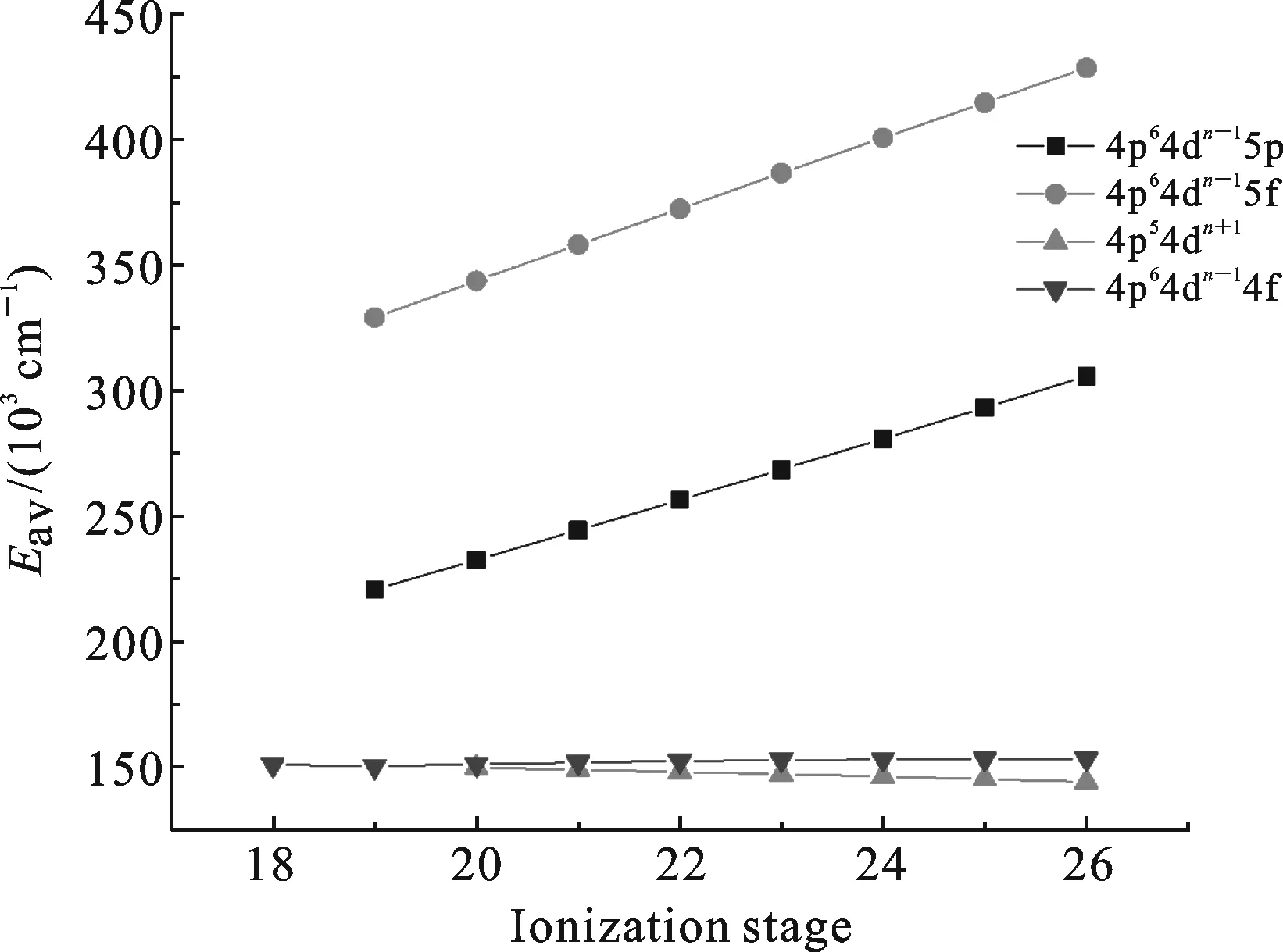
图1 4p54dn+1、4p64dn-14f、4p64dn-15f、4p64dn-15p和4p64dn(n=3～ 10)组态平均能随电离态的变化

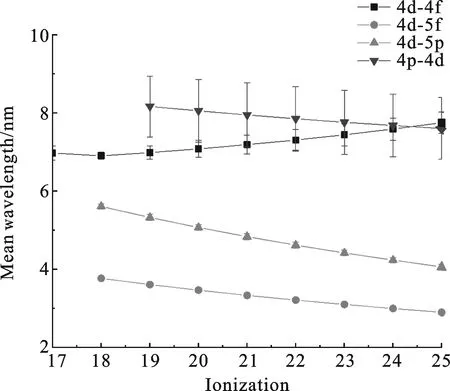
图2 4d-4f, 4d-5f, 4d-5p和4p-4d跃迁平均波长随电离度的变化

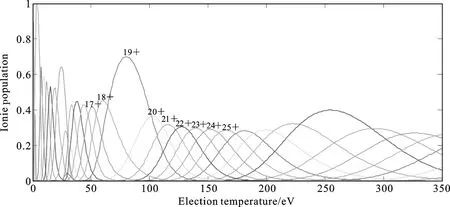
图3 不同电子温度下的Gd离子丰度

表1运用UTA统计理论计算在1 ～ 9 nm的光谱范围内，Gd17+～ Gd25+的4d-4f和4d-4p跃迁的平均波长等一系列参数，并运用计算的参数绘制4d-4f, 4d-5f, 4d-5p和4p-4d跃迁平均波长随电离度的变化图，如图 2所示.使用碰撞辐射方法[17]进行等离子体建模运算，电子密度取1021cm-3，得到离子丰度随电子温度变化的数据，离子丰度表示该温度下各个离子所占的相对强度大小，如图3所示，离子丰度从高到低的排列顺序为Gd19+，Gd18+，Gd17+，Gd20+，Gd21+，Gd22+，Gd23+，Gd24+，Gd25+.图4中将文献[18]中的144 eV电子温度下的实验光谱数据与本文中用Cowan计算得出的Gd跃迁辐射光谱数据相比对应良好，并在6.76 nm处提供最大强度.该合成谱是将Gd17+～ Gd25+理论计算的跃迁谱线按照图3计算得到的离子丰度的贡献率合成在一起得到的，使用高斯展宽类型，展宽值为0.02 nm，理论上的合成谱与实验谱吻合较好.

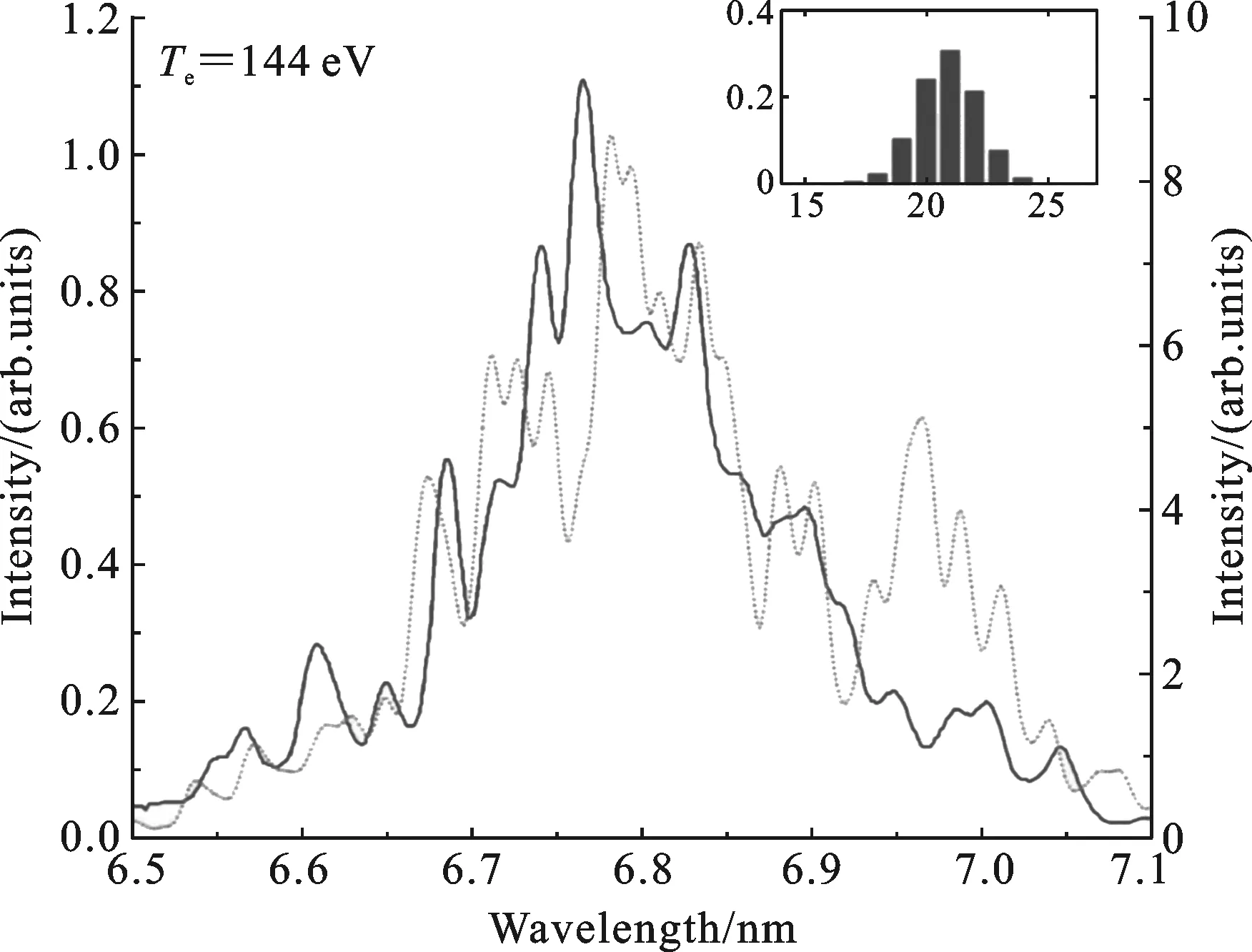
2.2 计算不同离化度Gd离子的谱线分布使用Cowan程序计算Gd离子跃迁时，考虑组态之间的相互作用，初始组态包括4p54dn+1,4p64dn-14f和4p64dn-15f，末态包括4p64dn,4p64dn-15s和4p64dn-15d.在Gd XVIII ～ Gd XXVI范围跃迁谱线非常密集，产生不可分辨跃迁峰(UTA)[19-20].实际测量不同离化度下Gd离子光谱中的各个谱线时，存在增宽效应，如仪器增宽，多普勒展宽等，使测量光谱变宽，因此对计算得出的跃迁光谱进行高斯线型展宽，展宽值为0.02 nm，与实验所采用的光谱仪的仪器展宽值一致.下面将分别给出Gd XIX ～ Gd XXVI下单组态和多组态(CI)两种情况下的谱线分布(图5).

表1 Gd XVIII ～ Gd XXVI光谱谱线范围内4d-4f、4d-5p、4d-5f和4p-4d跃迁的UTA[16]统计数据

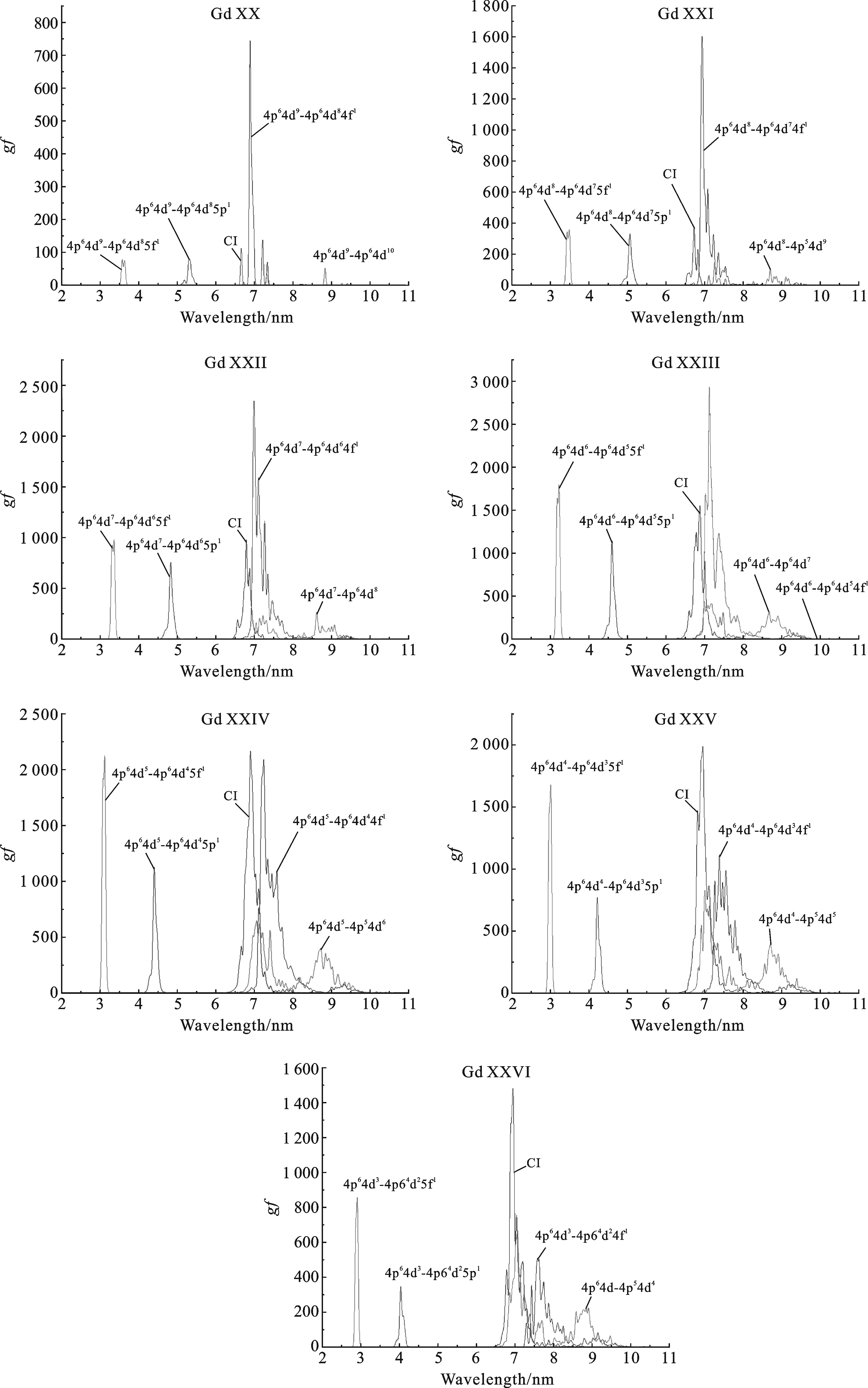
图5 组态相互作用对Gd离子4p-4d, 4d-4f, 4d-5p, 4d-5f跃迁谱线分布的影响

从图5可以看出，不同离化度下4d-4f和4p-4d跃迁产生的UTA谱线重叠较多，并且分布在我们研究的6 ～ 10 nm之间，而4d-5f和4d-5p跃迁产生的UTA谱线没有重合，且分布在我们研究的波长范围之外.当考虑组态相互作用(CI)的时候，谱线分布的范围变小，相比长波部分的波峰峰度降低或者几乎消失，整个谱线向长波方向移动.在不同离化度下组态相互作用的强弱也有不同的，对于4p64dn-15f和4p64dn-15p组态而言，随着离化度增加，波长向短波方向移动，与4p-4d和4d-4f跃迁产生光谱没有重叠，因此在组态相互作用的时候这两个组态对整个谱线的分布影响相对较小，而4d-4f产生的谱线逐渐向着长波方向移动，4p-4d跃迁产生的谱线逐渐向着短波方向移动，随着离化度增加，4p64dn和4p64dn4f组态之间的重叠部分逐渐增加，因此，两者之间的组态相互作用逐渐变强.

3 结语

本文中运用Cowan程序从理论上计算Gd17+～Gd25+跃迁产生的4p-4d，4d-4f，4d-5f和4d-5p的跃迁光谱，分别给出在单组态和多组态两种情况下的谱线分布状况，通过系统的理论计算可以得到以下3点结论：

1)4p64dn-15p,4p64dn-14f和4p64dn-15f的组态平均能随着离化度的增加而变大.

2)当考虑组态间相互作用时，谱线分布范围明显变窄，整体谱线向着长波方向移动.

3)对于本文中研究的钆离子跃迁来说，组态相互作用对谱线分布影响最大的2个组态是4p54dn+1和4p64dn-14f.

本文中提出的理论结果将对亚10 nm EUV光刻光源的研究具有一定参考价值.