高速磁悬浮列车悬浮架结构可靠性研究

李 强，姚毓瑾,虞大联，袁雨青

(1.北京交通大学 机械与电子控制工程学院, 北京 100044；2. 中车青岛四方机车车辆股份有限公司,山东 青岛 266111)

电磁悬浮型磁浮列车是一种靠磁悬浮力来推动的现代高科技轨道交通装备，依靠电磁力实现列车与轨道之间的无接触悬浮以及导向功能，再利用直线电机牵引列车运行.悬浮架是整个磁悬浮列车中主要的安装基础与承力部件之一，其设计制造的安全性以及结构的可靠性十分重要[1].

近年来，针对悬浮架的相关研究取得了大量研究成果.Sarunan[2]研究了中低速磁浮列车在碰撞、驱动过程中应当遵守的基本准则;Han等[3]主要针对中低速城市磁浮列车在试验台上进行疲劳强度试验评价；杨磊等[4-5]对中低速磁浮列车悬浮架在不同工况下进行静强度有限元分析，找出应力薄弱位置；谢鸣等[6-7]应用Ansys软件对高速磁浮悬浮架的托臂、Z向支撑、摇枕等关键部件进行静强度分析，为悬浮架部件有限元模型的创建提供了一定的参考.由上述文献可知，目前国内外对低速磁悬浮列车悬浮架结构可靠性方面的研究比较成熟，然而高速磁悬浮列车悬浮架的结构和受载方式与低速磁悬浮列车悬浮架有较大差别.高速磁悬浮列车悬浮架在实际运行时承受着复杂的交变载荷，极易产生疲劳损伤，因此对高速磁悬浮列车悬浮架可靠性的研究显得十分重要.本文作者针对中车青岛四方机车车辆股份有限公司设计的时速600 km的高速磁浮列车悬浮架，分析了悬浮架结构之间的连接方式，用Hypermesh软件完成了有限元模型的建立，根据实际受力情况，设计出一套加载及约束方案；依据高速运行下的载荷数据，并利用Ansys有限元分析软件从静强度、疲劳强度以及模态三方面对悬浮架的可靠性进行了研究.

1 悬浮架有限元模型

1.1 结构介绍

600 km/h高速磁悬浮车辆结构分为三部分：磁浮转向架(悬浮架)、二系悬挂部分和车体.悬浮架由横梁框架、悬浮框架以及纵向连接结构组成，见图1.其中横梁框架包括两根横梁、摇枕支梁和空气弹簧支梁；悬浮框架包括两个托臂和上下连接件；纵向连接结构包括纵梁、铰链和摆动柄.一个横梁框和两个悬浮框架组成悬浮框单元，两个悬浮框通过纵向连接装置构成悬浮架[7]，每一个部件之间由螺栓及铆钉连接组成.与传统转向架概念相区别，在磁悬浮悬浮架中，橡胶悬挂(电磁铁悬挂)为一系悬挂，摇枕空簧部分为二系. 二系悬挂是连接车体和悬浮架的主要构件，既是承载装置，又是活动关节，还能隔离高频振动.悬浮架部件材料主要包括EN AW-6005A T6、ZL101A和40CrMo.其中，因为摆杆是车体与悬浮架重要的连接结构，也是主要传力构件，所以采用40CrMo，其余材料均为铝合金材质.在有限元建模时，需正确模拟悬浮架部件之间的连接关系.

1.2 关键部位建模方法

1.2.1 机械连接方式

悬浮架主体采用铝合金材料，铝合金的机械连接方式主要包括铆钉连接和螺栓连接.铆钉和螺栓的连接方式通过耦合与约束方程法进行模拟.螺栓预紧力的处理方法为等效力法，即可以加快计算速度，又可以正确反映整个悬浮架的受力情况.

1.2.2 二系悬挂

二系悬挂系统结构主要包括空气弹簧支座、空气弹簧、摇臂、防滚件、摆杆和Y向限位弹簧等[8]，如图2所示.车体和悬浮架通过二系悬挂连接，车体和二系悬挂与摆杆之间均为球铰连接，二系中的摇臂和摇杆支架通过球铰相连，车体的侧滚转矩由滚动稳定器承受.在有限元分析软件中，选用Rndrelease命令创建球铰耦合；选用刚度合适的三向弹簧创建滚动稳定器和Y向限位弹簧，此建模方法的采用正确模拟了整个模型的自由度，从而建立了悬浮架二系悬挂结构模型.

1.3 有限元模型建立

采用Hypermesh软件对悬浮架进行有限元网格划分，为了提高有限元仿真的效率，对有限元模型进行了简化处理.通过抑制或者删除对实际问题没有影响或者影响很小的特征，减少了模型的特征数[9].悬浮架整体采用solid185单元进行网格划分，模型离散共有2 332 377个节点，7 610 622个单元.

2 边界条件与载荷工况

对悬浮架结构进行可靠性分析，一方面需要计算悬浮架的强度，另一方面考虑以模态为主的悬浮架动态特性.以头车第一悬浮架为例，首先定义坐标系的方向原则：纵向为车道滑移面的方向；横向为车道滑移面并垂直于行驶方向；垂向与滑移面垂直.本文分别给出了超常载荷和疲劳载荷的4个典型工况.

2.1 边界条件

在对悬浮架进行强度计算时的边界条件主要考虑约束与加载方式.悬浮架的作用是装载电磁铁，并将悬浮力、导向力、牵引力和制动力通过二系传递给车厢[10].根据悬浮架的实际运行原理，拟定垂向和横向约束在与车体连接的Z向支撑处，纵向约束在纵梁与牵引杆的连接孔处.根据悬浮架运行过程中的受力方式，在悬浮电磁铁安装座施加纵向和垂向载荷，导向电磁铁安装座施加纵向和横向载荷，连接摆杆处和裙板处均施加横、纵、垂三向载荷.

2.2 载荷工况

选取4种超常载荷工况对悬浮架进行静强度计算，如表1所示，并选取4种运营载荷工况对悬浮架进行疲劳强度的计算，如表2所示.

如表1所示，S3A/S5A为牵引工况，S5A在S3A工况基础上增加了转弯半径、加入了超高变化率、提高了风速并且加入了动态特殊载荷；S3B/S5B为制动工况，同理，S5B在S3B工况基础上增加了转弯半径、加入了超高变化率，提高了风速并且加入了动态特殊载荷.

表1 悬浮架静强度载荷计算工况表

如表2所示，A11A/A12A为牵引工况，A12A在A11A工况基础上加入了动态特殊载荷；A11B/A12B为制动工况，同理，A12B在A11B工况基础上加入了动态特殊载荷.

3 悬浮架可靠性研究

3.1 静强度计算结果

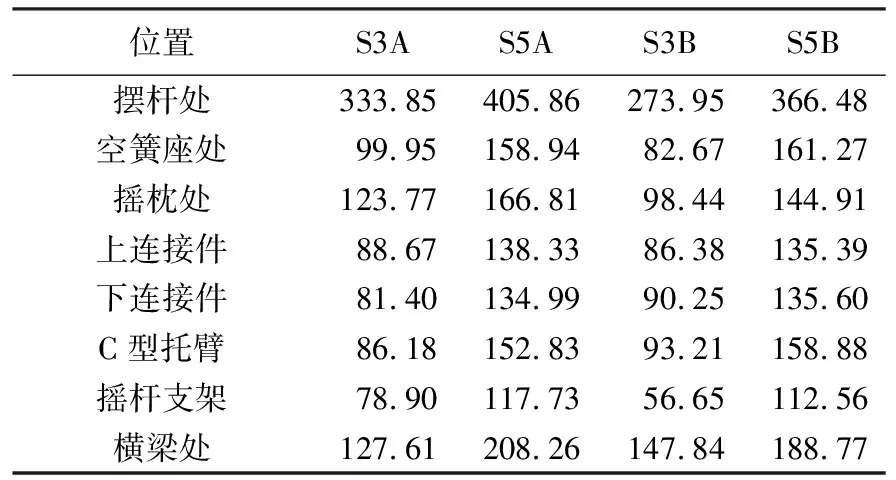
利用Ansys软件，按照表1所示的4个工况对悬浮架强度进行分析.一般来说，对于钢、铜、铝等塑性材料，可根据第四强度理论，选用Von Mises等效应力进行强度校核[11].4种工况下悬浮架最大应力计算结果如表3所示.

表3悬浮架超常载荷计算结果表

Tab.3Calculation results of the supernormal
load of levitation chassis MPa

位置S3AS5AS3BS5B摆杆处333.85405.86273.95366.48空簧座处99.95158.9482.67161.27摇枕处123.77166.8198.44144.91上连接件88.67138.3386.38135.39下连接件81.40134.9990.25135.60C型托臂86.18152.8393.21158.88摇杆支架78.90117.7356.65112.56横梁处127.61208.26147.84188.77

由表3可知，4种工况下最大应力均发生在摆杆处，应力最大为405.86 MPa，出现在S5A工况下，悬浮架在此工况下整体应力分布如图3所示.

摇枕、上连接件、摇杆支架、横梁处最大应力分别为166.81 MPa、138.33 MPa、117.73 MPa和208.26 MPa，均发生在S5A工况下；C型托臂、下连接件和空簧安装座处最大应力分别为158.88 MPa、135.60 MPa和161.27 MPa，发生在S5B工况下.

如表3所示，以S3A工况和S3B工况为例，摆杆、摇枕以及摇杆支架位置的应力值偏差较大，主要原因为二系悬挂装置为活动关节，起到一定减振作用，牵引和制动工况下的纵向加速度相反，会导致应力值偏差较大；空簧座、下连接件、C型托臂以及横梁位置的应力值偏差较小，主要原因是这些结构为主要的承载装置，牵引和制动工况下的应力值偏差较小；以S3A工况和S5A工况为例，S5A工况转弯半径更大，加入了超高变化率，提高了风速并且加入动态特殊载荷，因此悬浮架每个结构在S5A工况下的应力值均大于S3A工况.

3.2 疲劳强度计算结果

悬浮架在实际服役的过程中，承受复杂的载荷状态，包括垂向载荷、横向载荷和纵向载荷等，对悬浮架进行疲劳分析采用ERRI B12/RP17中多轴应力转化为单轴应力[12]，然后结合Goodman曲线评定结构疲劳强度.常用的多轴应力转单轴应力法主要包括：最大主应力法、等效应力幅和等效应力均值法、等效应力幅和sines等效应力法[13].由于最大主应力转换方法与标准推荐的试验测试一致[14]，采用最大主应力法进行转化，其疲劳强度评估数据见表4.最大主应力法具体步骤为：计算悬浮架结构在4种运营载荷下的应力大小，根据悬浮架结构形式和静强度分析结果选取应力较大的部位以及容易发生应力集中的节点作为考核对象，确定这些部位主应力值及其方向余弦.选择所有工况下主应力值最大的方向为基本主应力方向，并将此应力值作为最大主应力σmax，然后将其他工况下的主应力投影到最大主应力的方向上，从而选择最小的投影值作为最小主应力σmin，平均应力σm和应力幅值σa，采用下式计算，计算结果见表4.

表4 最大主应力法疲劳强度评估数据

σm=(σmax+σmin)/2

(1)

σa=(σmax-σmin)/2

(2)

利用悬浮架主要材料ZL101A绘制Goodman曲线，将表4中每个节点以平均应力作为横坐标、应力幅值作为纵坐标放入疲劳极限图内，结果如图4所示.由图4可知，所有关键点的应力值和应力幅值都比较小，悬浮架上所选关键点的应力值和应力幅值均在材料修正的Goodman疲劳极限内，说明悬浮架部件在整个使用寿命内不存在局部应力过大的现象，即悬浮架每一个结构的疲劳强度满足要求[15].

3.3 模态计算结果

采用有限元分析软件对悬浮架模态进行研究，分析悬浮架在某一频域内各阶模态振型及其频率，评定其动态特性能否满足设计要求[16].

采用Block Lanczos法对悬浮架进行自由模态分析，去除刚体模态后，表5列出了悬浮架前10阶弹性振型及其固有频率值.高速磁浮车辆的激振频率为8 Hz，由表5可知悬浮架横向弯曲、纵向弯曲和竖向弯曲频率均远高于激振频率8 Hz，且具有丰富的振型.前四阶振型如图5所示，悬浮架第一阶模态振型是两个悬浮框带着纵向连接件横向弯曲，悬浮架第二阶模态振型是前后悬浮框上下摆动产生纵向弯曲，悬浮架第三阶模态振型是前后悬浮框横向及纵向的弯曲，悬浮架第四阶模态振型是前后悬浮框向内侧摆动形成竖向弯曲.

表5 悬浮架模态计算结果

相比于传统转向架，悬浮架的自振频率比较低，悬浮架的纵向扭转、横向弯曲和竖向弯曲刚度较小，这有利于机械解耦以及悬浮架的曲线通过，这也是悬浮架结构特点之一.

4 结论

1)利用材料的屈服极限对悬浮架静强度进行评估.在四种超常载荷工况下，最大应力出现在S5A工况下，最大应力部位出现在摆杆处，应力值为405.86 MPa，小于40Cr的屈服强度850 MPa，其余部件的应力也均小于各材料的许用应力，悬浮架静强度满足要求.通过对应力值进行比较，发现悬浮架在有动态力的作用下，应力强度明显高于无动态力作用的工况.

2)利用材料Goodman曲线评估悬浮架的疲劳强度，选取13个危险参考点进行疲劳评定，从Goodman曲线图可知，所有危险点都在曲线的包络线范围之内，说明结构的疲劳强度满足要求.

3)在Ansys软件中利用Block Lanczos法对悬浮架进行模态分析.根据悬浮架前10阶模态的振型和频率可知，悬浮架的自振频率明显高于激振频率，不会产生共振现象.相比于传统转向架，悬浮架自振频率比较低，便于悬浮架机械解耦以及曲线通过，动态特性满足设计要求.

4)针对高速悬浮架有限元建模方式、约束方式以及加载方式提供了新方法，通过此方法可以校核悬浮架的应力强度，为以后有关高速磁悬浮悬浮架的疲劳强度试验奠定仿真基础.