数学现象教学视野下的起始课
【摘要】现象教学强调“回到问题本身”,它的起始课主张从真实的现象出发,通过观察和思考,形成学生自己的表达(知识)。对于概念和结构,应当着眼于自然生成。现象教学不排斥讲授法,但只能讲授学生无法生成的内容;现象教学也不排斥情境教学,真实的情境就是现象。
【关键词】起始课;现象教学;弧度制
【中图分类号】G633.6【文献标志码】A【文章编号】1005-6009(2020)11-0043-05
【作者简介】孙四周,江苏省苏州市吴江盛泽中学(江苏苏州,215228)教师,正高级教师,江苏省特级教师。
起始课除了引入课题、介绍核心概念以外,往往会呈现对课题的整体看法以及研究的方法和路径,给后面的课程定下基调。因此起始课素为教材编写者所看重,也往往是教师着力最深的地方。
课题怎么引入?核心概念从哪里来?这就牵涉知识观、学生观和教学观了。现象教学主张直面真实的世界,通过对现象的观察、思考而形成心理表征和符号表征,即形成属于自己的语言表达,这就从根本上杜绝了简单灌输。下面就以“弧度制”教学为例,谈一谈现象教学视角下的起始课教学。
一、问题本身
“回到问题本身”是现象教学的主张,研究什么就直接面对它。当然这要求教师对课程有个明确的定位,即“它究竟是什么”。
用现象教学的观点看,这节课的“问题本身”不是弧度制,而是“角的度量”,弧度制只是“度量”方式之一。要让学生面对一个几何实体———角,而不是面对一个知识点———弧度制。如此一来,学生要做的事情就很多了,比如:明显可感觉到角是有大小,但什么是“角的大小”,怎樣进行角的度量、有哪些可能的度量方式、为什么要引进弧度制,以及什么是弧度制、它从哪里来又到哪里去……说穿了,“角”是一种现象,“角的度量”是人类活动,“弧度制”是人类活动的成果:用“1弧度”作为单位来度量,比较简单,更容易被应用,因此就更为重要,也就被当作了一个重要范式,并被上升为科学或文化,如是而已。
笔者的教学设计如下。
师:请同学们拿出纸和笔,一起画三角形。
师:先随便画一个三角形。接着,画一个小一点的三角形、再画一个更小的、更小的、小到看不见……
回到第一个三角形,现在来画一个大一点的、再画一个更大的、更大的、大到超出纸面,甚至可以超出这个宇宙……
这些三角形小到看不见,大到超出宇宙,它们的内角和———
生:都等于180毅。
师:大大小小的三角形,内角和都一样,为什么?
生:因为角的大小与边的长短无关,角的边是射线。
师:所以,我们度量角并不是度量角两边的长度。那是度量什么的?
生1:度量角对边的长度。
师:那么是不是对边越长,角就越大?
生2:不是。度量角所对的弧的长度。
师:是不是所对的弧越长,角就越大?
生3:还不是。是度量角所对弧的度数。
师:什么叫弧的度数?
生3:就是看那段弧含有多少度。
师:那么,1毅的弧是怎么定义的?
生:就是一个圆周的360分之一。
师:很好。我们回到了角度制的定义,就把问题看清楚了。“1毅角”是指圆周360分之一的弧所对的圆心角。那么,这里定义的1毅角与圆的半径长短有关系吗?
生:没有,都是把圆周360等分,每个圆的每一个份所对的圆心角都相等,都是1毅角。
师:那么,给你一个圆,你会把它360等分吗?
生:不会。
师:如此说来,要得到1毅的角并不容易。
生:用量角器。
师:量角器也是人造出来的,又该怎样制作量角器上的刻度线呢?实际上,人类需要测量的东西很多,最容易测量的是什么呢?
生:是长度。
师:那面积呢?体积呢?
生:面积、体积等都不是直接测量的,是通过长度计算出来的。
师:是的。就算是温度、重量、电流强度等,这些与长度无关的量,也都转化为对长度的测量,比如温度计、杆秤、电流表等。就是对时间的测量,也是转化为长度的。这些都不奇怪,人的眼睛能够看到的就是长度。那么,角的测量是不是也这样呢?
师:现在,你自己可以画一个圆周……但是你手里并没有它的360分之一,你有什么呢?
生:有半径。
师:如果我们用半径长来量出一段圆弧,再画出这段圆弧所对的圆心角,是不是可以确定出一个角来?
生(疑惑):什么叫“确定出一个角”?
师:在不同半径的圆中,长度等于半径长的弧所对的圆心角是否相等呢?
我们来画几个看看(图1)。
操作:拿出几段长度不同的漆包线(软硬适度,便于弯折的那种,颜色要鲜艳一点)。用这些长度做半径画同心圆,再把漆包线弯成弧形,截取一段弧,画出所对的圆心角。
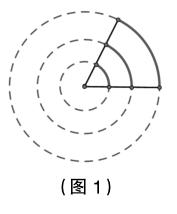
由此可以看到,在不同的圆里,弧长等于半径长的弧所对的圆心角大小相等。这个角很特别,我们就称它是1弧度的角,记为1rad。教师写出完整定义(此处略)。
师:定义1rad的角,是想干什么?
生:可以用这个角去度量其他角。
师:你能画出2rad的角吗?
生:两个半径长的弧所对的圆心角,用半径长的漆包线截取两次即可。
师:3rad的角呢?
生:截3次。

上述的教学过程,不是告诉学生什么样的角是1rad,而是从“怎样度量角”开始,把这个当作问题的起源,也是活动的出发点。很自然地发现可以用“手里已有”的半径作单位,于是引进了一种度量形式。或许有人会说,如果用半径当弦,不是也可以定义一个圆心角(这个角是60毅)吗?问题是,如果用“等于半径的弦所对的圆心角当作1个单位”,长度等于2个径的弦所对的圆心角就不是2单位,这不符合我们的几何直观。当然,如果学生没有提出这样的问题,教师不必要主动涉及(为了保持生成的流畅性)。类似的,大圆和小圆中,长度等于半径的弧所对的圆心角相等,这一点也不用刻意去证明。

二、联系与结构
任何一个独立的概念都是没有价值的,也是不容易记住的。在新的概念形成后,就要和原先的认知体系建立联系,向着结构化方向发展。
师:我们来画一个稍微大一点的角,6弧度的。
说明:上面已经画过2弧度、3弧度的角,可是在画6弧度的角时学生犹豫了起来。原因是:“6弧度的角”有没有超过1周角?这不是能用眼睛看出来的,必须经过精细的计算。

但是,新的疑惑又出现了,那就是“到底算多少弧度?”
师:2仔到底算多少?可以彼此讨论一下。
这里要注意的是,学生眼里的数学和教师是不一样的,特别是初学者。上面的活动是学生自己发现2仔抑6.28,虽然所花时间比较多,但这是体验的过程,有其价值。能夠生成的知识就不能不经讨论或思考而直接告诉学生,这是现象教学的“生成性原则”。
师:仔是个实数值,大约是3.14。如此2仔= 6.28>6,于是知道1周角大于6弧度。
师:再请问直角是多少弧度?


师:用什么办法来度量它?
生:应该用弧长量出一半径,可是又没有弧长没有半径。
师:确实,给你一个直角,它没有自带圆周。有办法吗?
生:作一个圆周。

上面做了两个方面的事情,一是给定弧度数,画角;二是给定角,“度量”出它的弧度数。延续了“角的度量”的初衷,并把数学定义落实到具体情境中。在“求直角的弧度数”的时候学生还需要人为添加一个圆,这是对概念的应用,也加深了他们对弧度制的理解。
在这个过程中出现了“360毅=2仔弧度”,自然导出弧度制和角度制的换算。在应用中理解,在应用中感悟出新的知识,是很好的策略。

三、背景与展望
一般来讲,起始课会介绍知识的产生背景、逻辑演进并对应用前景作出展望,这其实是哲学基本问题“我是谁、我从哪里来、我到哪里去”的具体化。现象教学的起始课同样要关注这三个问题。介绍历史事实,容易找到知识的固着点;理解逻辑顺序,容易建立知识结构;展望应用前景,可以提高学习兴趣、增强学习动机。
笔者在这一部分的教学设计如下:

师:角的弧度数上限可以到多少?下限可以到多少?中间可以取哪些值?
生:正的可到无穷大,负的可到无穷大,中间可以取任意实数。
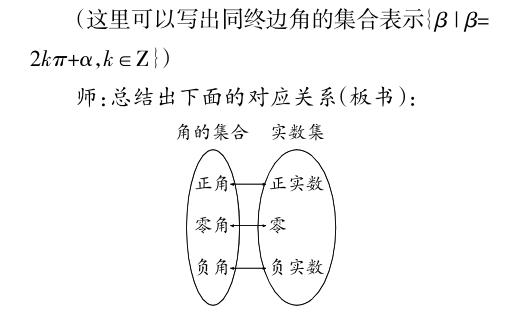
接下来是历史介绍,从度分秒制、弧度制、密位制,谈角的度量演化史,让学生了解人类的探索历程,在具体教学时可详可略。
在谈背景与展望时,应当注意以下几点:
(1)注重人类思想进步的脉络,略去琐碎的细节,对细节的过分关注不利于对事物的整体理解。
(2)描述前景时应向学生介绍能听懂的,或者稍加解释就能听懂的部分,完全听不懂的则不介绍。比如在本节课上,就不适合介绍炮兵是怎样用“密位”瞄准目标的,尽管它很有趣。
(3)起始课上要不要介绍整个课程(一整章或一整节)的概念图?笔者认为没有必要,除非学生能懂。当然,概念图在总结课上是很有价值的。
四、结语
鉴于起始课为后续教学“定了调”,故尤其要“以学定教”。
教师对知识的了解肯定远远多于教材所给予的,因此要注意别把课堂变成知识的展示。弧度制这节课,笔者反复让学生画图,就是要让他们充分活动,以获得切身体验,体验过的才能被感悟。现象教学不排斥讲授法,但只能讲授学生无法生成的内容,比如学术名词、人为约定、专用符号等;现象教学也不排斥情境教学法,真实的情境就是现象。因此,现象教学可以吸收以前诸多教学法的优点,使得学生在真实的现象面前进行真实的思考、获得属于自己的实在的知识。
给予学生知识,他们能学会,路径是了解、理解、掌握、应用、综合、评价;给予学生现象,他们能用数学的眼光观察它、用数学的思维思考它、用数学的语言表达它。虽然最后都能得到知识,但后者才更直接指向核心素养。如果进行层次上的区分,则现象是形而下的,知识是形而上的。所以,现象教学与知识教学的区别,主要是观念上的而不是技术上的。现象教学着眼于人的发展,而不是让人去继承或记忆(知识)。
【参考文献】
[1]何睦,罗建宇.高中数学章节起始课的教学研究与案例设计[M].哈尔滨:哈尔滨工业大学出版社,2019.
[2]孙四周.现象教学[M].长春:吉林教育出版社,2019.
[3]水菊芳.从情境到现象:再进一步的数学教学[J].教育研究与评论:中学教育教学,2018(03):10-14.
[4]孙四周.现象教学的内涵与价值[J].教育研究与评论:中学教育教学,2018(03):5-9.
[5]李宏铭.数学现象教学的实施及评价概述[J].教育研究与评论:中学教育教学,2018(03):15-19.

