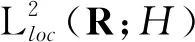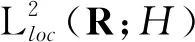无界域上非自治随机反应扩散方程一致随机吸引子的存在性
,
(河海大学理学院,江苏南京210098)
本文研究定义在全空间Rn上具可加噪声的反应扩散方程解的渐近行为:
du=(γΔu-λu-f1(u)-a(x)f2(u))+g(x,t)dt+h(x)dω,
(1)
初值为
u(x,0)=u0(x),x∈Rn,
(2)
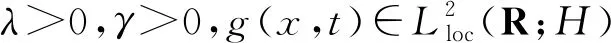
f1(s)s≥α1|s|p-β1|s|2,f′1(s)≥-c,
(3)
f2(s)s≥α2|s|p-β2,f′2(s)≥-c,
(4)
|f1(s)|≤α3|s|p-1+c1,|f2(s)|≤α4|s|p-1+c2,
(5)
其中αi>0,i=1,2,3,4,βi>0,i=1,2,c>0,c1>0,c2>0;α1>β1,λ>2β1。假设a(x)∈L1(Rn)∩L∞(Rn),a(x)>0。
系统(1)~(2)是一非自治系统,含有确定的非自治项和随机项。随机项的存在,对于未来信息具有不可知性,在研究随机偏微分方程时,传统吸引子的概念(见文献[1-3])已无法应用。Flandoli等人在文献[4-6]中将传统吸引子的概念加以推广,提出了拉回吸引子的概念,并给出了相应的存在性刻画定理;之后,Wang在文献[7-8]中对含有确定非自治项的随机偏微分方程吸引子的存在性加以研究,通过引入2个驱动动力系统,给出了随机吸引子存在的充分必要条件,且对吸引子的结构加以刻画;对确定非自治系统一致吸引子的研究见文献[9];近期,源于文献[9]中的思想,Cui等人在文献[10]中研究含有确定非自治项随机偏微分方程关于确定非自治符号一致拉回意义下吸引子的存在性,并给出相应的判定定理; 关于随机偏微分方程的其他研究见文献[11-15]。
本文应用文献[6,13]中的方法,研究式(1)~(2)关于确定非自治符号随机一致吸引子的存在性。由于式(1)~(2)是定义在全空间上,Sobolev嵌入缺乏紧性,本文采用空间分割的方法,通过在余空间中估计解一致性来得到紧性结果。
令‖·‖和(·,·)分别表示L2(Rn)上的范数和内积,‖·‖p表示LP空间上的范数,字母C表示一般的正常数,其值可以在不同行或同一行有所变化。
1 预备知识
本节给出随机动力系统的一些概念和理论,详见文献[8,10,13,16]。
令(X,d)为可分的Banach空间,X上的非空集间的Hausdorff半距离定义为
对于任意度量空间M,定义B(M)为其上的σ-代数。令(Σ,dΣ)为紧的Polish度量空间,且在下面意义下是不变的:
θtΣ=Σ,∀t∈R,
其中θ为光滑的平移算子,满足:
①θ0是Σ上的恒等算子; ②θs∘θt=θt+s,∀t,s∈R; ③(t,g)θtg是连续的。
同时,定义(Ω,F,P)为概率空间,定义在其上的动力系统{ϑt}t∈R满足:
①ϑ0是Ω上的恒等算子; ②ϑtΩ=Ω, ∀t∈R;
③ϑs∘ϑt=ϑt+s, ∀t,s∈R; ④(t,ω)ϑtω是(B(R)×F,F)-可测;
⑤P-保测:P(ϑtF)=P(F),∀t≤0,F∈F。
分别作用在Σ和Ω上的2个群{θt}t∈R和{ϑt}t∈R称为基流。
定义1称φ(t,ω,g,x):R+×Ω×Σ×XX为定义在X,(Σ, {θt}t∈R)和(Ω,F,P, {ϑt}t∈R)上的非自治随机动力系统,如果
①φ是(B(R+)×F×B(Σ)×B(X),B(X))-可测的;
②φ(0,ω,g,·)是X上的恒等映射,∀g∈Σ,ω∈Ω;
③对每个固定的g∈Σ,x∈X,ω∈Ω,有如下余圈性质成立:
φ(t+s,ω,g,x)=φ(t,ϑsω,θsg)∘φ(s,ω,g,x), ∀t,s∈R+。
令D是X中的随机集族组成的集合。
定义2称K=K{K(ω)}ω∈Ω为φ的一致D-吸收集,若对任意ω∈Ω和B∈D,都存在T=T(ω,B)>0,使得
φ(t,ϑ-tω,Σ,B(ϑ-tω))⊂K(ω),∀t≥T,
其中
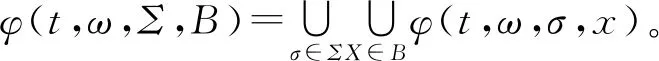
称K=K{K(ω)}ω∈Ω为φ的一致D-吸引集,若对任意ω∈Ω,有

定义3称定义在Banach空间X上的连续随机动力系统φ是一致D-渐近紧的,若对任意B∈D,ω∈Ω,{tn},0 定义4称随机集A={A(ω)}ω∈Ω为φ的D-(随机)一致吸引子,如果A属于D,且是最小的紧一致D-吸引集。 定义5称随机有界集{B(ω)}ω∈Ω关于{ϑt}t∈R是缓增的,若对所有的β>0,ω∈Ω,满足 定义6[10]假设φ是关于符号空间Σ和X连续的非自治随机动力系统。若φ有闭的一致D-吸收集B∈D,且φ在X上是一致D-(拉回)渐近紧的,则φ有唯一的一致D-吸引子A={A(ω)}ω∈Ω∈DX,其中 (6) ②g的壳是平移不变的,即H(g)=θtH(g),∀t∈R; ⑤对任意σ∈H(g),成立η(σ)≤η(g)。 (7) 为了定义式(1)~(2)所对应的随机过程, 考虑概率空间(Ω,F,P),其中, Ω={ω∈C(R,R):ω(0)=0}, F为Ω的紧开拓扑所诱导的Borelσ-代数,P为(Ω,F)下的双边Wiener测度。定义变换: ϑtω=ω(·+t)-ω(t),∀t∈R,ω∈Ω, 则P是遍历的且在ϑ作用下具有不变性,见文献[17]。定义 (8) 则z(ω)是一维Ornstein-Uhlenbeck方程 dz(ϑtω)+λz(ϑtω)dt=dω (9) 的一个稳态解。此外对每个ω∈Ω,z(ϑtω)关于t连续,随机变量|z(·)|是缓增的,即对每个ε>0,满足 (10) 令v(t)=u(t)-hz(ϑtω), 其中u是问题(1)~(2)的解, 那么v满足 (11) 初值为 v(x,0)=v0(x)=u0(x)-hz(ω)。 (12) 对每个t≥0,ω∈Ω,g∈H(g0)和u0∈H,令 φ(t,ω,g,u0)=v(t,ω,g,u0-hz(ω))+hz(ϑtω), (13) 则φ(t,ω,g,u0)是问题(11)~(12)对应的非自治随机动力系统。 令DH是H中的缓增集组成的集合,即 易知,DH是包含封闭的吸引域。 为了证明对应于式(1)~(2)的随机动力系统φ一致DH-吸引子的存在性,需要对式(1)~(2)的解建立一致估计。首先证明φ存在一致DH-拉回吸收集B。 φ(t,ϑ-tω,H(g0),D(ϑ-tω))⊂B(ω), 其中B(ω)定义为 (14) C和η(g)为正常数,z(ω)为式(8)给出的缓增随机变量。 证明在L2(Rn)中用v和式(11)作内积, 得 (15) 对上式进行逐项估计,应用式(3)、(5)和Young不等式,并由p>2,得 (16) 同理,应用式(4)、(5)可得 (17) 注意到 (18) 令λ1=λ-2β1,由式(15)~(18)可得 (19) 由h(x)∈H2(Rn)∩W2,p(Rn)∩L1(Rn),得 (20) 对式(20)两边同乘eλ1t,将ω和g分别替换成ϑ-tω和θ-tg,并在(0,t)上积分,得 (21) 因为v0∈D(ϑ-tω),由D的缓增性,存在T=T(ω,D)>1,使得 (22) 由式(13)知结论成立。证毕。 (23) 证明令vgn和v分别为方程(11)对应于gn和g的解,令ξ=vgn-v,则 (24) 由式(3)和Young不等式,式(24)右边第1项可估计为 (25) 其中0<θ<1。由式(4)和Young不等式,式(24)右边第2项可估计为 (26) 其中0<θ<1。式(24)右边第3项可估计为 (27) 由式(24)~(27),可得 (28) 用Gronwall不等式,可得 (29) 证毕。 (30) 证明令ρ为R上的光滑函数,且对任意s∈R+,有0≤ρ(s)≤1, (31) (32) 下面对式(32)逐项进行估计。首先有 (33) 注意到 (34) 由式(33)~(34),可得 (35) 对于非线性项部分有 (36) 如同式(16)~(17)的推导,并应用式(3)~(5)可得 (37) 考虑式(32)右边最后部分,有 (38) 由式(32)~(38)可得 (39) 对式(39)在(T1,t)上用Gronwall不等式(T1>T),得 (40) 用ϑ-tω和θ-tg代替ω和g,对所有的t≥T1,有 (41) 下面对式(41)中右边各项进行估计。首先对右边第1项,由引理1,存在T2>T1,使得对t≥T2,有 (42) 对于第2项,由式(22)可得,存在R1>0,当k≥R1,t≥T2时, (43) 同样,对于第3项,存在R2>0,使得对k≥R2,k充分大,t≥T2时,有 (44) (45) 由h(x)∈H2(Rn)∩W2,p(Rn)∩L1(Rn),存在R4>0,当k≥R4时,有 (46) 同样,对式(41)右边第5项,有 (47) 令R*=max{R1,R2,R3,R4},T*=max{T1,T2},对k≥R*,t≥T*,有 (48) 即 (49) 故 (50) 证毕。 证明由引理2知,式(1)~(2)的解关于初值Lipschitz连续,应用引理1~3及Aubin-Lions定理,如同文献[18]中引理2.4的证明即得。 证明由引理1及引理3,并应用定义6即得结论成立。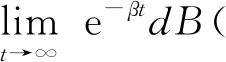
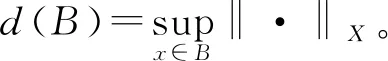

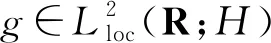
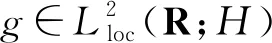
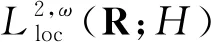
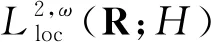

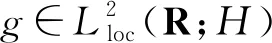
2 式(1)~(2) 对应的随机动力系统
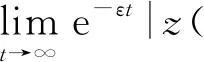
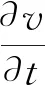
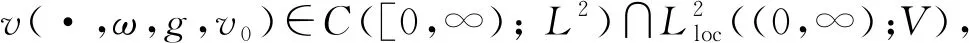
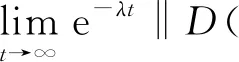
3 解的一致估计

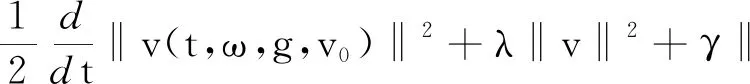
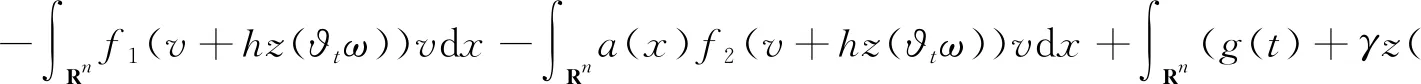
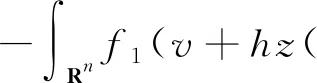
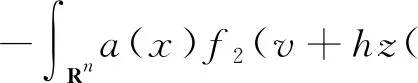

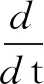
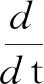

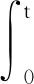
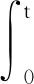

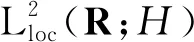
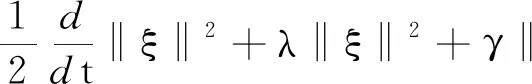
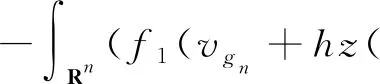
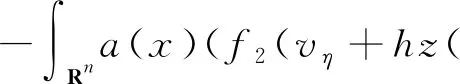
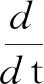
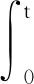
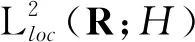
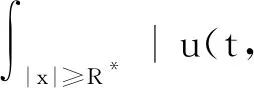
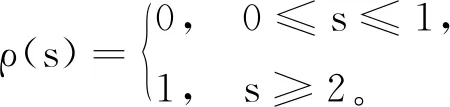
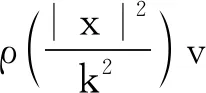
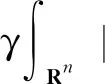
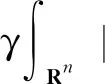
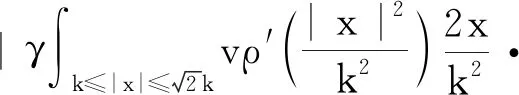
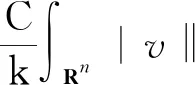
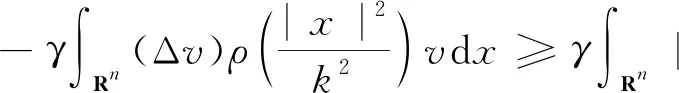
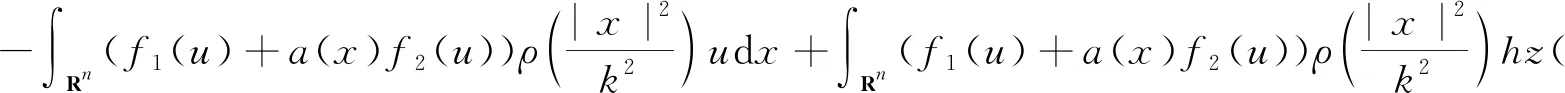
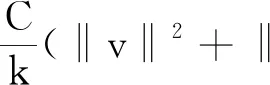
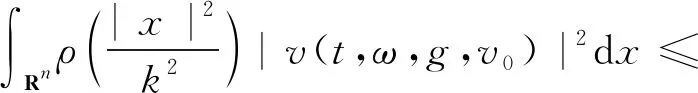
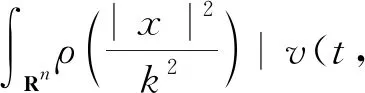
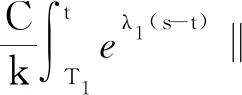
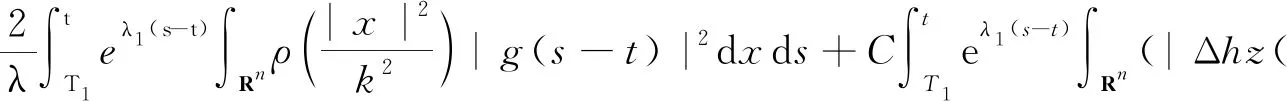
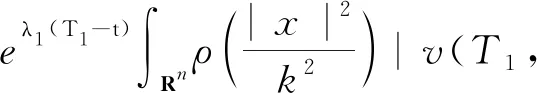
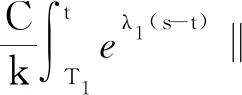
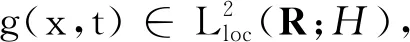
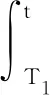
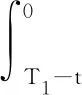
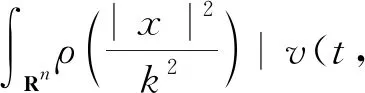

4 一致随机吸引子的存在性