一道竞赛试题的解法探究及其应用

广东省中山市濠头中学 (528437) 闫 伟

1.试题呈现

例1 (2019年全国高中数学联赛四川预赛试题)设点A的坐标为(0,3)，点B,C为圆O:x2+y2=25上的两动点，满足∠BAC=90°，求ΔABC面积的最大值．

分析：本赛题以圆为背景，考查了圆的标准方程、几何性质、不等式等知识以及转化、数形结合等数学思想，突出考查学生对数量关系进行转化与运算能力以及推理论证能力，对考生的思维水平和数学素养有较高的要求；试题平中见奇，内涵丰富，解法多样，是一道值得探究的好题.

2.解法探究

解法1：如图1所示，设B(x1,y1),C(x2,y2),P(x,y)为线段BC的中点，则有

图1

评注：本解法是参考答案提供的，在解决过程中先利用B,C点坐标确定线段BC中点P的轨迹，再根据点P的轨迹计算中线长AP的范围，然后利用均值不等式将直角三角形的面积转化成关于三角形斜边中线的表达式，体现了转化的思想及坐标法的运用.

图2

评注：解法2从三角函数的视角解题，引入角∠OAB作为参变量，根据定长OA计算点O到两直角边的距离，然后根据勾股定理用角∠OAB表示两直角边AB,AC从而得出面积关于参变量的表达式，再利用柯西不等式和三角恒等变换解决面积最大值；相比较解法1，虽然运算量不少，但利用函数和不等式的思想方法是解决几何中最值的常用方法，这种通性通法在数学解题中起着至关重要的作用，在平时的解题教学中要注重这种通性通法，重视知识的生成过程，培养学生分析、解决问题的能力.

图3

先给出矩形的一个性质：如图3，已知P为矩形ABCD内一点，则|PA|2+|PC|2=|PB|2+|PD|2.

证明：以AB,AD所在直线为x,y轴建立平面直角坐标系，设A(0,0),B(a,0),C(a,b),D(0,b)，另设P(x,y)，则有|PA|2+|PC|2=x2+y2+(x-a)2+(y-b)2,|PB|2+|PD|2=(x-a)2+y2+x2+(y-b)2,显然有|PA|2+|PC|2=|PB|2+|PD|2.下面用此结论解决上面的赛题.

图4

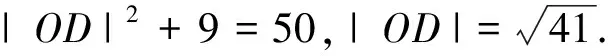
评注：解法3借助了平面几何中矩形的一个优美结论，先通过直角构造矩形，利用矩形结论确定OD长度和矩形对角线AD，再引入∠CAD作为参变量表示三角形的面积，结合三角形的边与边关系建立面积的不等式，从而计算面积最大值；本解法相比较前2种解法，纯粹从平面几何的角度思考，巧借矩形结论，简化了推理和运算过程，具有直观、简洁的特点，方法新颖独到.在各类试题中具有隐性矩形的问题可以参考此法.

3.拓展应用

上述解法是借助矩形的性质巧妙解决了与面积相关的线段长度问题，进而达到解决面积最值这一目标；解析几何通常用代数的工具解决几何问题，平常解题中我们注重解几的代数运算，轻视了几何推理；实质上解析几何问题的本质是几何问题，它们本身包含一些重要的几何性质，若能挖掘出题目中蕴含的平面几何元素，充分利用平面几何知识，则可以避开繁琐的运算，使解题过程简化，方法简洁优美，更好的揭示这类问题的几何性质.因此，解析几何问题应该将解析法与平面几何方法相结合，通过深思引领运算，从而得到解题的最优方法，这不仅是解决几何问题减少运算的法宝，还可以更好的提高解题能力 .下面就这一性质的应用做些拓展研究，能快速有效的解决这一类问题，可谓是“小结论，大用途”.

图5

图6

例3 如图6，在平面坐标系xOy中，已知B,C为圆x2+y2=4上两点，点A(1,1)，且AB⊥AC,则线段BC的长度的取值范围是.

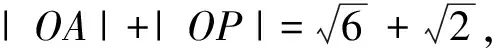
评注：通过直角关系构造矩形,结合矩形性质确定动点P的轨迹方程，再将线段BC的长度转化成动点P与两定点O、A的距离的关系从而得出结果，解题过程直观、简洁.

图7

解：如图7,设椭圆的左右焦点为F1,F2,设PA,PB与椭圆相切(切点为A,B)，且PA⊥PB.作F1关于PA,PB的对称点分别为F1′,F1″，连接F1F1′,F1F1″分别于PA,PB交于M,N两点.由椭圆的光学性质可知：F1,A,F2三点共线，F1″,B,F2三点共线.因为|F2F1′|=|AF1|+|AF2|=2a,所以得|OM|=a；同理|F2F1″|=

|BF1|+|BF2|=2a,得|ON|=a，由于F1MPN为矩形，于是有|OF1|2+|OP|2=|OM|2+|ON|2,所以|OP|2+c2=2a2，又c2=a2-b2，故|OP|2=a2+b2,从而点P的轨迹方程为x2+y2=a2+b2.

评注：上述结论中的点P的轨迹就是著名的蒙日圆,借助矩形的性质和椭圆的光学性质可以快速的得到结论，相比较传统的方法利用切线的斜率作为参量，联立直线与椭圆计算而言，极大的减少运算和推理论证过程，充分体现了妙用平面几何性质巧解解析几何问题的思想方法.

5.结语

数学家波利亚曾说过：“掌握数学就意味着善于解题” .引导学生学会解题是数学新课标教学的重要组成部分；数学问题的解决仅仅是一个开端，更重要的是解题后的反思与回顾；遇到一道经典题目，需要从多角度、深层次探求其解法，从不同的思维角度分析同一道试题，可以得到不同的解法，从数学知识本身的角度看，可以发现知识之间的相互联系，体会转化的过程，还可以构建知识网络体系，从而学生在学习过程中不仅掌握了基本的解题技能，还培养了思维的广阔性、深刻性、灵活性以及创新性，让学生对学习内容有一个整体认识，并将知识融会贯通，举一反三，开阔视野，活跃思维，才能实现解题研究价值的最大化.