2019年天津理科卷第8题的解法探究

广东省湛江一中培才学校 (524037) 曾肇玲

2019年天津理科卷第8题在函数情境下，以导数、函数性质、不等式知识为载体，在基础知识交汇处精心设计．不等式恒成立是常规题型，构思于分段函数之上，围绕高中数学内容主线，聚焦学生对重要数学概念、定理、方法、思想的理解和应用展开，独具匠心，别有一番新意．考生需整合自身基本活动经验，在分类讨论、数形结合、转化与化归等数学思想引领下，发现问题的关键、提出等价问题，作出认真分析，去除非本质因素，才能最终接近并揭示问题的数学本质．

1.试题呈现

A.[0,1]B.[0,2]C.[0,e]D.[1,e]

2.命题赏析

素养导向视角下审视这道试题，对考生核心素养予以较好的考查．数学抽象现于“特值检验”、“构造等价问题模型”；几何直观下的“数形结合”；“分类讨论”中严密的逻辑推理；参数和变量混合处理过程的数学运算和数据的分析，巧妙地把内隐于考生思维品质的数学素养外显于可视的解题行为中．并且试题情境熟悉平和，条件简单清晰，表达言简意赅，构思巧妙．有效规避“题型”、“套题”，核心素养导向下，以能力立意，注重数学本质、通性通法、淡化解题技巧，在朴实中重“四基”，常规中考“四能”．此题在2019年高考数学试题中独树一帜，对高考备考有引领示范作用，亦是教学中提升学生核心素养的贴切范例和难得的素材．

3.试题求解分析

(1)特值排除

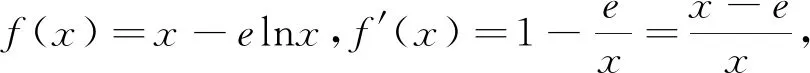
评析:从应试的角度看，上述过程简便、快捷、准确，俗称“特值法”、“排除法”．这是由客观题的形式所决定的一种求解探究过程，通过特例归纳，获得合情结论．这也是数学抽象核心素养最朴素、最原始的表现.

(2)分段讨论

f(x)≥0在R上恒成立等价于：“x≤1时，x2-2ax+2a≥0恒成立”且“x>1时，x-alnx≥0恒成立”．

(ⅰ)x2-2ax+2a≥0在(-∞,1]上恒成立.

思路一：二次函数模型

解析:考查二次函数f(x)=x2-2ax+2a，x∈(-∞,1]，只需f(x)min≥0.

当a≥1时，f(x)min=f(1)=1>0，符合f(x)≥0;当a<1时，f(x)min=f(a)=a2-2a2-2a≥0，得0≤a≤2，故0≤a<1.综上a≥0．

评析:二次函数是高中数学最重要的一个函数，其与二次不等式、二次方程密切相关．二次不等式在x∈(-∞,1]恒成立转化为二次函数给定区间求最值问题，由于对称轴不确定，导致需分类说明．

思路二：分式函数模型

对于g(x)max的求解，可作如下不同考虑：

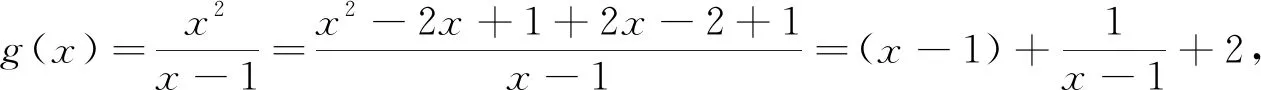
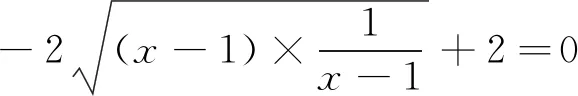
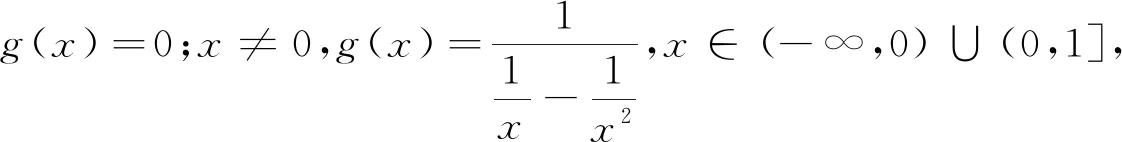
g(x)max=0，所以a≥0．

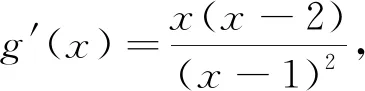
方法四：(整体观察)注意到x2≥0，x-1≤0，所以g(x)≤0，所以a≥0．

(ⅱ)x-alnx≥0在(1,+∞)上恒成立.

思路一：利用条件所给函数

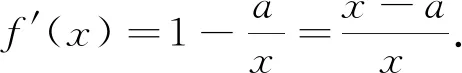
思路二：参变分离构造新函数

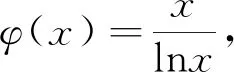
思路三：构造两个函数

解析:原不等式等价于x≥alnx，x∈(1,+∞)恒成立，只需直线y=x在y=alnx的图像的上方.

图1

当a≤0时，显然不等式成立;当a>0时，直线y=x与y=alnx的图像相切时，如图1.

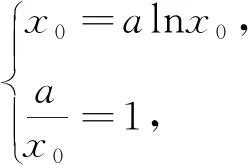
a=e，所以a≤e．综上，可见a∈[0,e]，故选C．

评析：不同视角下，有不同的解决思路．思路一参变混合求解，a与区间(1,+∞)的关系不确定，是导致讨论的原因．为避开讨论，思路二进行了参变分离，而思路三是基于几何直观考虑，给抽象的数学问题几何直观，以揭示问题的数学本质．

4.解题启示

解题教学中应规避“题型”、“套题”的模式化重复训练．解题教学是高三教学的主要形式，学生的操练必不可少，但一味大量训练，反复总结题型，对各种问题进行“分门别类”，期待考试的时候能对号入座，以不变应万变．这种高考备考模式，极易形成学生的思维定式，当面对规避“题型”、“套题”模式化的高考试题时，学生将会束手无策，望题兴叹，或者是漏洞百出．这就要求教师在教学是要充分发挥示范作用，使学生经历从观察、感悟到学会对问题的审视、思考、调整、优化的解决过程，并通过知识整合、方法的回顾、途径的优化、思想的领悟，深化对问题数学本质的认识．只有这样，遇到相关问题是才能随机应变，快速确定最佳的解题方案．可见，问题解决只是手段，培养学生的数学能力和学科素养才是最终目标．