接触爆炸和近距离爆炸比冲量数值仿真研究

李臻， 刘彦， 黄风雷， 闫俊伯， 余文力， 吕中杰

(1.北京理工大学 爆炸科学与技术国家重点实验室，北京 100081；2.火箭军工程大学 核物理学院，陕西,西安 710025)

炸药的爆炸是一种极为迅速的化学能量释放过程，在此过程中，爆炸释放的能量转变为爆轰产物的热能、动能及周围介质传播的冲击波能量. 爆炸产生的比冲量及其空间分布特征是判定爆炸毁伤模式和定量分析毁伤效果的基础，因而准确获得不同工况下的爆炸比冲量具有重要意义.

中远距离爆炸，构件的毁伤主要由空气冲击波引起，由于炸药位置距离构件较远，在空气冲击波的传播过程中，冲击波峰值压力面逐渐趋于一个球面，球面上超压分布趋于相同，因而可近似为点源强爆炸，由爆炸相似率可知，入射超压是比例距离的唯一函数. 亨利奇等[1-2]根据实验结果拟合关于冲击波超压和比例距离的方程式，在工程上获得了较高的精度和便利性.

对于近距离爆炸甚至接触爆炸，炸药爆炸产生的产物喷射和空气冲击波的3维分布不均衡，受炸药形状、起爆点位置、炸药靶板相对位置的影响较大，给理论分析带来较大困难. 随着计算机硬件和数值仿真技术的发展，使用数值仿真技术模拟爆炸现象的精度和可信度越来越高. 汪维[3-5]、师燕超等[6-8]使用流固耦合方法对比例距离在0.4～2.0 m/kg1/3之间爆炸毁伤混凝土构件的效果进行数值模拟，得到了和实验值较吻合的结果. Li等[9]通过实验的方法研究了接触爆炸和近距离爆炸下P-section钢筋混凝土梁的毁伤行为，得出爆炸贯穿和震塌极限. Liu等[10]利用实测冲击波超压数据推导了近距离爆炸下钢筋混凝土梁中心点的运动，与实验结果吻合较好. 而对于比例距离小于0.5 m/kg1/3甚至接触爆炸的数值模拟方法仍待进一步研究. 赵鹏铎[11]进行了迎爆面涂聚脲结构抗40 g TNT外爆载荷试验，分析聚脲涂层对结构抗爆性能的影响. 候俊亮[12]使用AUTODYN仿真软件对球形及不同长径比圆柱形装药冲击波场及其传播过程进行数值模拟，得到了爆炸载荷下的挠度时间曲线. 以上研究针对的都是比例距离在0.4 m/kg1/3以上的中远距离爆炸载荷，对于接触爆炸和比例距离小于0.4 m/kg1/3的爆炸载荷却鲜有数值模拟研究. 本文使用PBM方法对接触爆炸和近距离爆炸载荷进行建模，使用Nansteel实验数据对模型进行校核，继而对等长径比TNT柱形炸药爆炸后比冲量进行数值模拟.

1 数值模拟验证

Nansteel[13]通过实验方法研究了C4球型装药近距离爆炸下的比冲量，实验装置如图1所示，整个实验场地被一块金属隔板分为两个区域，左侧为炸药爆轰区域，右侧为实验测量区域，测试子弹放置于隔板中央的孔洞中. 当左侧的C4球形装药爆炸后，子弹在爆轰产物和冲击波的作用下向右飞行，右侧的高速摄像系统捕捉到飞行轨迹并计算速度，继而换算成爆炸比冲量. 实验中使用的C4质量为227 g，爆心和靶板之间的距离分别为5.08，7.62，10.16，12.70，15.24，19.05 cm. 实验结果见表1.

Nansteel实验结果见表1，子弹抛掷速度和比冲量随着爆心距的增加而降低，爆心距为5.08 cm的比冲量是爆心距为19.05 cm的比冲量的12.3倍，在炸药质量均为227 g的情况下其爆炸比例距离仅变化了3.75倍.

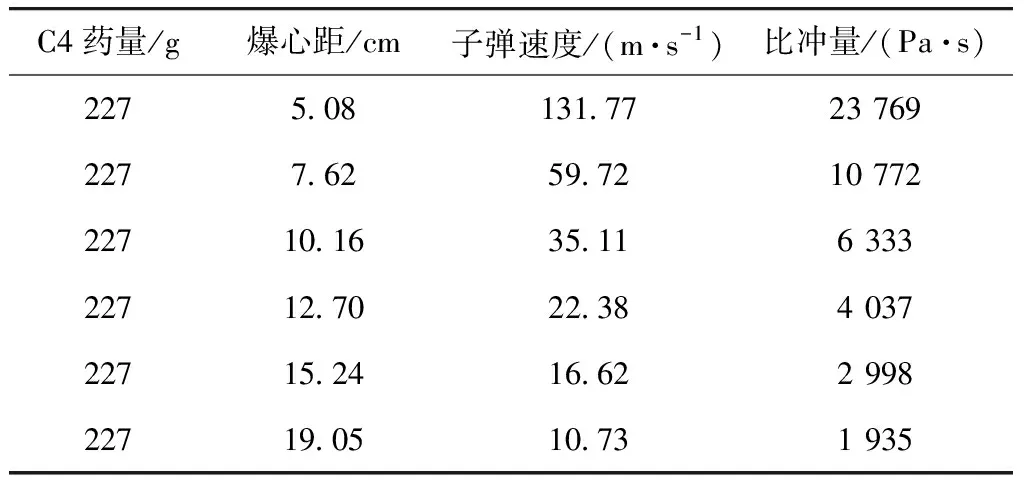
表1 Nansteel实验工况Tab.1 Nansteel experimental conditions

PBM方法[14]是一种为气体动力学模拟开发的粗粒度多尺寸粒子方法，基于麦克斯韦方程建立. 这个方法基于如下假设：① 炸药有大量粒子组成，这些粒子表现为有强度的球体，处于恒定的随机运动状态；② 粒子比分子之间的距离大得多；③ 粒子的运动遵循牛顿运动定律；④ 粒子与粒子之间的碰撞和粒子与物体之间的碰撞是完全弹性的；⑤ 粒子之间没有吸引力或排斥力.

通过将许多分子(1018量级)组成为一个粒子，结合系统自由度的降低和时间步长的增加，PBM可以对整个爆炸过程中宏观系统进行求解计算. PBM方法建立仿真模型包含拉格朗日算法的六面体子弹单元和炸药的PBM粒子，子弹采用理想弹塑性本构进行计算，C4炸药的PBM参数设置见表2.

表2 PBM参数Tab.2 PBM parameters

为验证仿真方法和材料参数在所有的6个比例距离上全部适用，根据球形炸药中心起爆后爆炸场的对称性，采用一个模型6种工况同时计算的方法进行仿真，即在炸药周向360°的区域内均匀分布6枚子弹. 当炸药爆炸后PBM粒子扩散并撞击子弹，推动子弹运动，仿真过程过程如图2所示.

PBM方法得到的子弹速度随时间变化趋势如图3所示，在炸药爆炸后，6枚子弹获得速度，在100 μs时子弹速度基本趋于稳定，距离为5.08 cm的子弹最终速度为134 m/s，距离为7.62 cm的子弹最终速度为61.3 m/s，距离较远的4枚子弹速度介于13.0～37.3 m/s之间.

同时使用Ls-dyna的流固耦合方法对Nansteel实验进行数值仿真，即炸药域和空气域使用欧拉算法计算，子弹使用拉格朗日算法计算，两者之间通过设置*CONSTRAINED_LAGRANGE_IN_SOLID关键字进行耦合. 炸药选用JWL状态方程[15]，Jones-Wilkins-Lee(JWL)状态方程是一种不显含化学反应、由实验方法确定参数的半经验状态方程，能比较精确地描述爆轰产物的膨胀驱动做功过程. 仿真使用的JWL状态方程参数源自文献[16]，具体参数见表3.

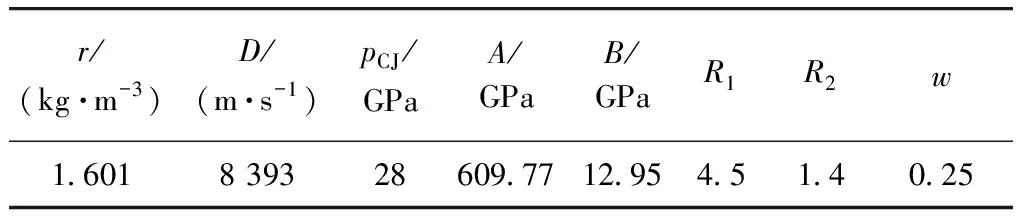
表3 C4炸药JWL状态方程参数Tab.3 JWL parameters of C4

流固耦合方法得到的子弹速度随时间变化趋势如图4所示. 在炸药爆炸后，6枚子弹获得速度，在100 μs时子弹速度基本趋于稳定，距离为5.08 cm的子弹最终速度为90.1 m/s，距离为7.62 cm的子弹最终速度为43.2 cm，距离较远的4枚子弹速度介于8～25 m/s之间.

将流固耦合方法仿真结果、PBM方法仿真结果与Nansteel实验结果相比较，如图5所示. 对于所有6个距离，PBM方法计算得到的子弹速度与实验得到的子弹速度较为吻合，而流固耦合方法得到的子弹速度均偏低于实验结果，但随着比例距离的增加，流固耦合方法的误差也在逐步缩小. 对于19.05 cm距离的子弹速度预测，流固耦合方法和PBM方法得到的结果与实验值基本相同，说明在中远距离爆炸的模拟使用流固耦合方法和PBM方法均可，而对于接触爆炸和近距离爆炸PBM方法则更为适用.

2 接触爆炸和近距离爆炸比冲量仿真

在接触爆炸和近距离爆炸的过程中，爆炸产生的比冲量是一个在工程上非常重要却比较难获取的物理量. 基于PBM方法，本节对爆炸比冲量进行仿真，建立的仿真模型如图6所示，模型包括一个圆柱形TNT药柱和一个平板. 平板分为固定区域和可动区域，固定区域添加固定约束以减小侧向冲击波对可动区域的影响，可动区域由25个2 cm×2 cm×2 cm的方块组成，每一个方块设置为一个part，通过part速度得出迎爆面2 cm×2 cm的平均比冲量.

在爆炸冲击波的作用下，单个part获得一个很高的速度，在爆炸过程中即有明显位移，造成冲击波场的不连续，影响周围part的速度方向. 为减小part在爆炸过程中的位移，仿真模型中可动部分part使用弹性本构，密度为1.0×105g/cm3，弹性模量为2.0×105GPa，以模拟冲击波刚壁面反射. 反射比冲量为

I=mv/A,

(1)

式中，m=8.0×102kg，A=4×10-4m2，可化简为

I=2×106v.

(2)

2.1 等长径比圆柱形药柱接触爆炸比冲量

建立直径分别为3,4,5,6,7,8,9,10 cm的等长径比(L/D=1)的圆柱形TNT药柱，药柱密度为1.59 g/cm3，对应药柱质量分别为34,80,156,270,640,910,1 250 g，设定药柱上表面中心起爆，得到药柱正下方part的速度，从而计算得出等长径比圆柱形药柱接触爆炸2 cm×2 cm范围内平均比冲量，如图7所示.

由图7可以得出，当药柱直径由3 cm增加到10 cm时，中心part平均比冲量与药柱直径为一次函数关系，函数关系式为

I=kde+b，

(3)

式中：I为比冲量；de为药柱直径；k值为1.247×104Pa·s/cm；b值为-6 874 Pa·s.

2.2 接触爆炸和近距离爆炸比冲量分布

在接触爆炸和近距离爆炸的情况下，爆炸比冲量的分布对于后续结构响应分析十分重要. 本节仿真模拟密度为1.59 g/cm3的等长径比TNT药柱爆炸，直径设为8 cm，质量为640 g，为了研究不同爆炸距离下爆炸载荷的分布，设立了5个爆心距，见表4. 以药柱中心点在靶板上的投影点为圆心，半径为20 cm范围内的区域为主要研究对象，得到的比冲量分布见图8.

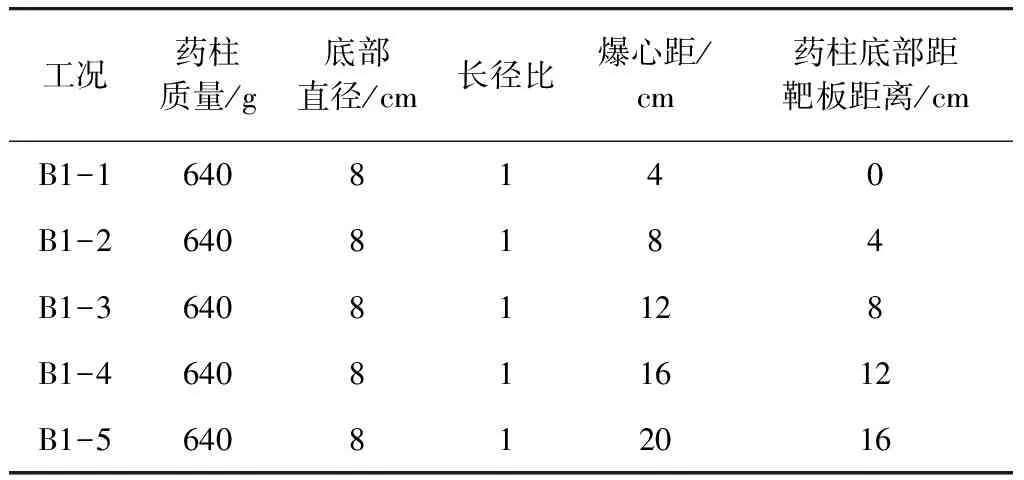
表4 仿真计算工况Tab.4 PBM parameters

从图8中可以看出，B1-1到B1-5工况，随着爆心距的增加，靶板每个位置的比冲量都在减小，半径0～6 cm范围内的比冲量受爆心距影响剧烈，半径6～10 cm范围内比冲量差异逐渐减小，半径10～20 cm范围内比冲量受爆心距影响非常微弱. 对于640 g等长径比TNT药柱接触爆炸和近距离爆炸的工况，可以认为爆炸比冲量集中在靶板中心点半径0～10 cm的区域内.

对于等长径比接触爆炸和近距离爆炸的工况，靶板任一位置的比冲量是炸药质量、爆心距和距靶板中心点的距离3个量的函数，对于等长径比的TNT药柱，由量纲分析可得

(4)

式中：w为药柱质量；I为比冲量；r为爆心距；d为距靶板中心点距离. 当药柱质量定为640 g时，可化简为

I=f1(r)f1(d)，

(5)

通过图中的数据进行函数拟合，

(6)

适用于640 g等长径比TNT药柱在比例距离为0.046 4～0.24 m/kg1/3爆炸后比冲量的计算，拟合R值为0.959，拟合结果与仿真结果的比较如图9所示.

使用同样的方法对直径和高度均为10 cm的1 250 gTNT药柱接触爆炸和近距离爆炸工况进行仿真计算，结果如图10所示，其中爆心距分别设置为5，10，15，20，25 cm. 对比图8和图10，比冲量的大体变化趋势相同，而1 250 g TNT爆炸的工况下比冲量下降趋势更为陡峭. 对于靶板中心点，在相同比例距离下1 250 g工况的比冲量为640 g工况比冲量的1.2～1.3倍，与式(4)的结论相吻合.

通过对1 250 g等长径比TNT炸药接触爆炸和近距离爆炸比冲量仿真结果的分析，得到比冲量I与距靶板中心点距离d、爆心距r的关系为

(7)

适用于1 250 g等长径比TNT药柱在比例距离为0.046 4～0.24 m/kg1/3爆炸后比冲量的计算，拟合R值为0.963，拟合结果与仿真结果的比较如图11所示.

3 结 论

本文开展了接触和近距离爆炸下比冲量的数值仿真计算，结合Nansteel实验结果，对比了流固耦合方法和PBM方法计算的准确度，采用PBM方法对不同直径等长径比TNT药柱接触爆炸的情况进行仿真计算，分析了靶板中心点的比冲量变化规律，通过改变爆心距，对640 g等长径比TNT药柱爆炸后20 cm半径内比冲量进行仿真，得出如下结论.

① PBM方法仿真得到的子弹飞行速度和Nansteel实验结果相当，流固耦合方法得到的子弹飞行速度低于Nansteel实验结果，PBM方法可以用于接触爆炸和近距离爆炸的仿真计算.

② 对于等长径比TNT药柱，接触爆炸靶板中心点比冲量和药柱直径是一次函数的关系，k值为1.247×104Pa·s/cm.

③ 通过改变爆心距，基于PBM方法对圆柱形药柱接触爆炸和近距离爆炸进行仿真，得到了比冲量的分布，并拟合了相应的经验公式.