网格类型对管内旋流特性数值计算的影响

陈科昊，王宗勇

(沈阳化工大学 机械与动力工程学院， 辽宁 沈阳 110142)

随着计算机技术和数值计算方法的高速发展，计算流体动力学(CFD)已成为解决科研问题的工具之一，它可以研究流体的运动规律，达到对物理问题进行研究分析的目的.在复杂情况下，实验测量往往很困难，甚至是不可能的，而计算流体力学则能方便地提供全部流场范围的详细信息.与实验相比，计算流体力学具有对参数限制少，费用少，流场无干扰的特点.

计算流体力学分析的一般过程为：将流动问题转化为成熟的数学模型描述；制定几何和流域模型；设置边界条件与初始条件；网格生成；设置求解策略参数；后处理等.在这些环节中，网格生成工作约占整个项目周期80 %～95 %，生成一套满足计算要求的网格对计算结果的准确性具有极大影响.如何高效地在复杂几何模型下生成易于计算收敛的网格[1]是当前CFD技术所面临的主要困难之一.

目前，CFD使用的网格生成方案有两种构造方式：结构化网格[2]和非结构化[3-4]网格.结构化网格的拓扑连接有很强的规律性[5]，每个节点之间关系分明，拓扑关系连接简单，网格生成的质量高，易收敛；非结构化网格是无规则的拓扑连接，需要记忆单元节点之间的联系，对网格节点缺少结构性的限制，在网格初步构造中，几何边界的复杂程度会造成局部网格数量过大，网格无法实际反映几何特征，导致网格质量下降，计算不易收敛，需要二次调整来提升网格质量.此外，非结构化网格节点分布的无规律性和数量不确定性，使由结构化网格发展起来的基于多邻点的高精度格式[6]难以应用于非结构化网格.

近年来，随着工业产品精度和性能的不断提升，对结构分析的精度和效率要求也相应提高，结构化网格受到越来越多的重视[7].但由于三维工程中几何形状复杂性，结构化网格尚不具有普遍适用性，非结构化网格也有实际研究意义.针对上述问题，本文对同种物理结构分别创建非结构化网格和结构化网格，从网格生成方式、耗时、收敛性、数据准确性等方面分析二者的异同，总结归纳内置旋流元件的管内流动区域结构化网格划分方法，为从事相关领域数值模拟研究的学者和工作人员提供一定借鉴和帮助.

1 网格概述

1.1 非结构化网格

网格区域内的内部点不具有相同的毗邻单元，即与网格划分区域内的不同节点相连的网格数目不同.在ICEM中设定网格类型和生成方法等参数后，软件自动求解得到的体网格.非结构化网格人工参与量较小，节点密度易控制，但网格填充效率不高，网格数量过多.

1.2 结构化网格

在网格区域内所有的内部节点都具有相同的毗邻单元，即内部不同节点相连的网格数目保持一致.结构化网格容易实现区域的边界拟合，网格光滑，易构建流体域和固体域，方便耦合计算，但对几何模型要求程度高，网格生成方式缺乏普遍适用性，人工参与量大.

1.3 网格种类及特性分析

2D模型常见网格类型有三角形网格和四边形网格；3D模型常见网格类型有四面体网格、五面体网格和六面体网格.四边形网格和六面体网格在CFD计算中有着不可比拟的优势，如在计算资源消耗和收敛速度方面，然而这种看法不全面，忽略了一些劣势方面，如网格的准备时间、以及一些不适用的场合.从计算原理考虑，网格越密，越能更实际反映几何特征，计算结果更加贴近实际，然而在仿真计算中，网格数量过多，计算时间会成倍增加，且计算的准确性和网格数量并不是成完全正比例关系，故在仿真计算与分析中应根据实际需求构造合适的网格种类及数量，最优地解决科研问题.

以2D为例，从计算精度角度而言，三角形网格利用周围3个节点的值，四边形网格利用周围4个节点的值，因此疏密相当的两种类型网格，四边形的计算精度高于三角形，但从计算资源消耗方面则正好相反.所以单纯从计算精度或计算资源消耗某一方面比较三角形网格和四边形网格孰优孰劣没有太大意义.

2 网格应用

2.1 几何模型及研究变量

选取内置全扭旋元件管作为指定模型，扭旋片轴线与管轴线重合，其结构如图1所示.管内径D=20 mm，管长L=400 mm，扭旋元件厚δ=1 mm.以管径作为雷诺数特征尺寸，即Re=ρu0D/μ，其中：ρ为流体密度，kg/m3；μ为流体动力黏度，mPa·s；u0为入口流体速度，m/s.通过数值模拟方法在Re=200～1 800范围内对全扭旋元件管的层流流体流动进行研究.分别建立非结构化网格和结构化网格，并与实验得出的经验公式进行对比，保证模拟结果能够满足准确度要求.探究两种网格建立方法对计算时间、收敛性和数据的影响.

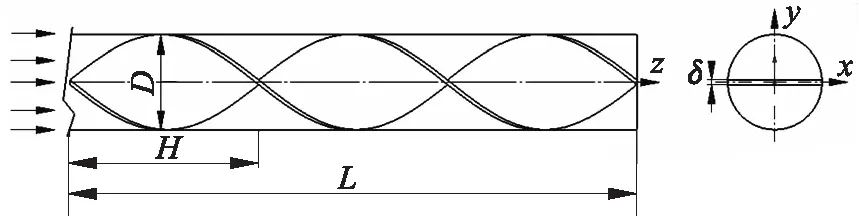
图1 全扭旋元件管的部分几何模型Fig.1 Partial geometric model of all-twist-screw element tube

2.2 网格划分

2.2.1 结构化网格生成流程

(1) 合理定义Part：由结构特征进行规律性命名，不需要对某些小区域单独建立Part.

(2) Block建立 ：操作虚拟块进行拓扑构建，将Block上的数据映射到真实的物理几何中，完成贴体网格的划分.

构建方法有2种：

自顶向下：创建初始整体Block，初始块是包裹整个几何空间的六面体块或四面体块.由于初始块往往难以满足要求，为使建立的块拓扑结构尽可能的与几何结构相贴近，需要对块进行切割、删除处理.

自底向上：由低级拓扑向高级拓扑的构建过程.结构复杂的拓扑结构可利用外部或内部O型、L型、C型等分块方式切割(见图2),有效提高网格质量.

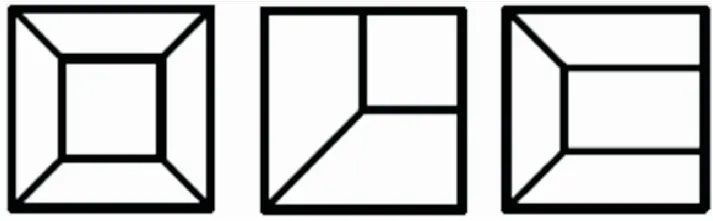
图2 O型、L型、C型分块方式Fig.2 O type，L type，C type block mode

(3) 建立映射关系、定义节点分布.

(4) 域的选取：块和域具有一一对应关系.

(5) 生成网格、检查网格质量、光顺网格、选择需要求解器导出网格.

2.2.2 结构化网格实例

生成结构化网格的基本思路：将2D块转化成3D块，进行块与关联操作，准确地将块上信息映射到几何上.图3为采用自底向上方式生成网格的转化过程.

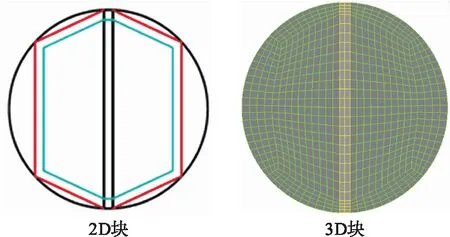
图3 结构化网格的生成转化Fig.3 Transformation of structured mesh generation

2.2.3 非结构化网格生成流程

(1) 几何准备：几何体本身不存在缺陷，如3D几何不能有缺失的面，不正常的面重叠，不存在面面相交干涉；保证简化的几何体能够反应真实的物理场景.

(2) 合理定义Part:根据实际几何模型的结构特征规律性地命名.某些截面积过小可单独命名.

(3) 全局网格参数设定：设定缩放因子、最大网格尺寸、面网格、体网格以及边界层网格；最大网格尺寸应小于待划分网格区域尺寸.

(4) 局部网格参数细化：对计算结果影响较大的区域定较小的网格尺寸，对计算结果影响较小的区域定较大的网格尺寸，在保证计算精度达到模拟需求下，减小网格规模，提高数值计算效率；局部网格参数优先级高于全局参数.

(5) 流体计算域的创建：选取表面或者利用材料点的方式创建Body.材料点(质心点)的选取[8]一般为某一指定点或者两点之间的中间点.

进行域的选取应遵循以下2种原则：1)确保准备建域封闭模型上两个基点，不可越过耦合面；2)两个基点间的质心点应在封闭模型内，即当封闭区域充满流体时，确保质心点完全浸没在流体中，不能与任意面接触.

(6) 网格生成、修补及光顺.

(7) 网格输出：设置目标求解器并输出网格.

2.2.4 非结构化网格实例

生成非结构化网格的基本思路：使用八叉树方法生成四面体网格，是一种自顶向下的网格生成方法，即先生成体网格，然后生成面网格.图4为采用自顶向下方式生成的非结构化网格.

图4 非结构化网格实例Fig.4 Unstructured mesh

2.2.5 网格评判标准分析

(1) 结构化网格质量评判标准

Determinant(2×2×2)：最小雅克比矩阵与最大雅克比矩阵行列式的比值.1表明质量最好，0表明质量最坏.本文结构化网格质量在0.6以上.

Angel:每个网格单元的最小内角要求大于18°.本文结构化网格单元最小内角大于27°.

(2) 非结构化网格质量评判标准

Quality:检测四面体、三角形单元质量要求大于0.3.本文非结构化网格质量在0.4以上.

Aspect Ratio：纵横比(最大/最小边长度的比例).本文非结构化网格纵横比为9，满足计算要求.

2.3 模拟方案

以液态水作为仿真计算介质，分析该不可压缩流体在管道内的稳态流动过程.在整体计算过程中，计算残差设定为10-6以下，且温度等残差曲线趋于稳定即说明求解过程已经收敛，计算前需假设流动状态确定后流体的各种物性参数基本维持恒定.

3 数值验证及收敛对比分析

3.1 网格无关性检验

为验证网格的独立性，在Re=600情况下对管内流动区域分别进行不同网格尺寸的结构化网格与非结构化网格划分，建立不同网格数量模型.以Nu作为传热评价指标，分析网格数量对传热性能的影响，结果如图5所示.

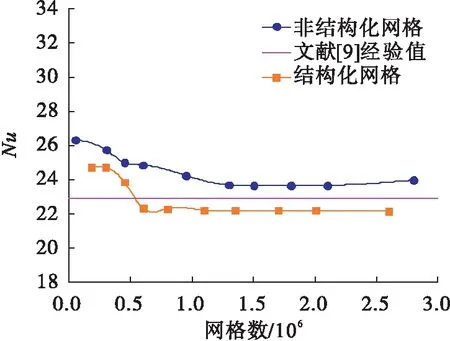
图5 Nu随网格数量的变化Fig.5 The variation of Nusselt with the number of meshes

由图5可以看出：随着网格数量的增多，努塞尔数逐渐趋于定值，非结构化网格数量接近1.3×106、结构化网格数量接近1.1×106时Nu已逐渐趋于定值.为了增加横向比较，将结构化网格与非结构化网格的计算结果与文献[9]研究结果进行比较，并以文献[9]结果为基准绘制相对偏差图，如图6所示.由此可以看出非结构化网格和结构化网格与文献[9]研究结果相对偏差随着网格的逐渐加密逐渐控制在10 %以内.

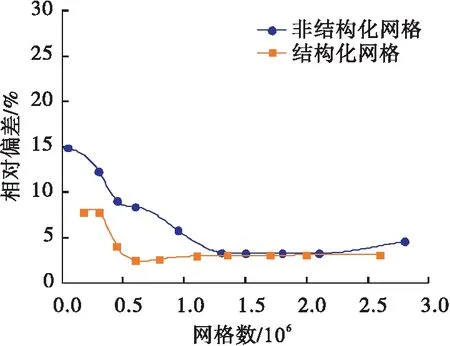
图6 本文结果与文献[9]的相对偏差Fig.6 The relative deviation between the results of this paper and the literature[9]

在保证计算精度的前提下，为达到较快的收敛速度，非结构化网格数量选用1.3×106左右，结构化网格数量选用1.1×106左右.

3.2 定性温度

管内流体温度取决于流体流动状态，同时流体温度也决定了流体物性，比如密度和黏度.为确定不同雷诺数下管内流体的定性温度，设定圆管壁温恒定为360 K.进口温度295 K，均匀分布.以换热管进出口长度范围内流体平均温度作为工质物性定性温度.图7显示了两种网格下的定性温度，可以看出整体存在差异，但实际差异值小于0.5 %.

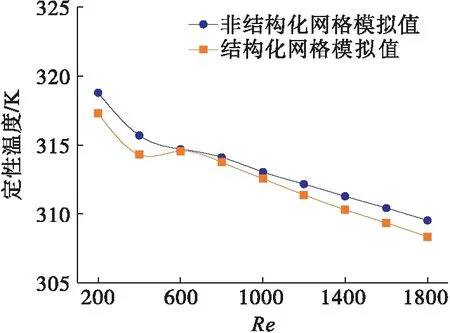
图7 不同雷诺数下两种网格流体的定性温度Fig.7 Qualitative temperature of two kinds of grid fluids under different Reynolds numbers

3.3 结构化网格与非结构化网格收敛残差与迭代次数对比

模拟过程计算收敛所对应的迭代次数、收敛时间或收敛残差可以表征网格类型的质量.为揭示结构化网格和非结构化网格对收敛过程的影响，绘制不同雷诺数下两种类型网格的收敛迭代次数和残差图，如图8所示.由图8可以看出：在任何雷诺数下数值计算收敛状态所需要的迭代次数和残差值均是结构化网格优于非结构化网格；随着雷诺数的增大，无论是结构化网格还是非结构化网格，收敛迭代次数和残差值均随之增大，而非结构化网格增大明显大于结构化网格，特别是Re>1 200以后，非结构化网格增大速度更为明显.结果表明结构化网格在模拟过程中特别是较高雷诺数下非结构化网格具有更高的计算效率和计算精度.

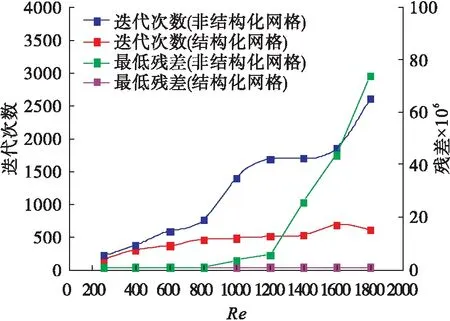
图8 结构化网格和非结构化网格模拟 迭代次数和残差对比Fig.8 Comparison of iterations and residuals between structured and unstructured grids

3.4 网格类型对传热性能影响

为确保多组流速下模拟计算的准确性和可信度，本文两种网格类型下的模拟结果与文献[9]实验结果进行比对，结果如图9、图10所示.

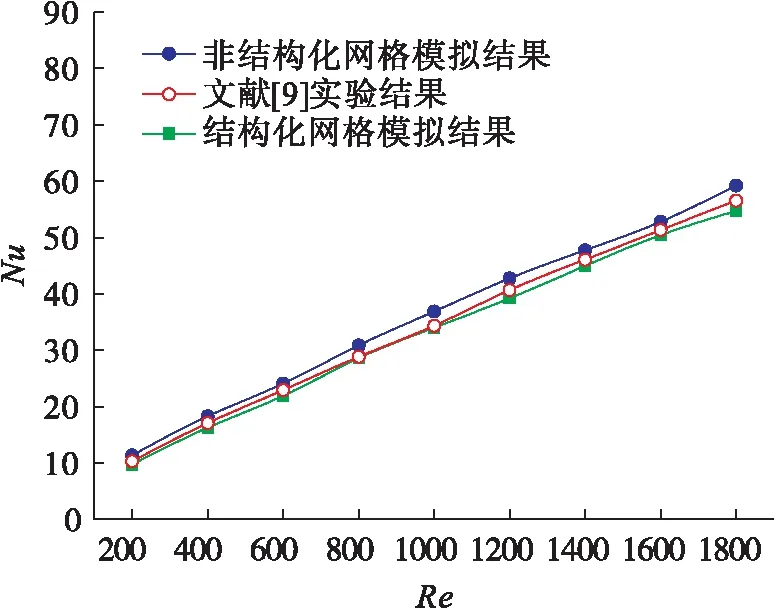
图9 雷诺数对努塞尔数的影响Fig.9 Effect of Reynolds number on Nusselt number

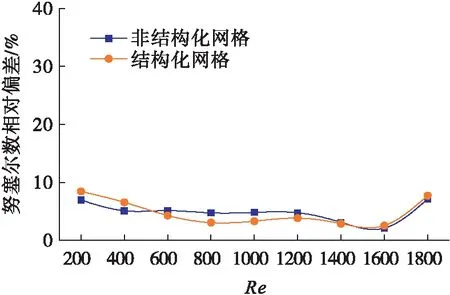
图10 结构化网格和非结构化网格努塞尔数相对偏差对比Fig.10 Comparison of Nusselt number relative deviation between structured and unstructured grids

Re<600范围内，非结构化网格和结构化网格均与文献[9]实验数据拟合良好，两类网格的模拟值偏差不大.在Re=600～1 600范围内，结构化网格的模拟值更贴近文献[9]实验结果；Re>1 600范围内，严格意义上管内流体流动进入过渡区域，模拟值与文献[9]实验结果误差都在10 %以内.

4 结 论

(1) 收敛性方面，结构化网格较非结构网格有明显地提升；结构化网格收敛速度能提高1倍左右，残差值始终可以达到最低标准.

(2) 以Nu作为传热评价指标，在Re<600范围内，非结构化网格和结构化网格均与文献[9]实验数据拟合良好，两类网格的模拟值偏差不大.在Re=600～1 600范围内，结构化网格的模拟值更贴近文献[9]实验结果；Re>1 600范围内，严格意义上管内流体流动进入过渡区域，网格类型已经不是造成差异的主要因素，计算模型的选取是主要原因.

(3) 相比非结构化网格，由于三维工程元件的复杂性，结构化网格生成方式缺乏普遍适用性，非结构化网格受结构特征影响较小，因此两种网格均存在实际研究意义，合理运用，才能达到对物理问题进行研究的目的.