基于潜隐变量自相关性子空间划分的故障检测策略

张 成，郭青秀，李 元

(沈阳化工大学 技术过程故障诊断与安全性研究中心, 辽宁 沈阳 110142)

随着现代工业生产过程对生产安全和产品质量要求的逐步提升，过程监控对于保障工业生产正常进行起着关键性作用. 统计过程控制(statistical process control，SPC)是基于统计方法对生产过程进行分析评价，根据反馈信息及时发现过程异常行为,以便进行后续调整[1].

主元分析法(principal component analysis，PCA)作为经典的SPC方法已经被广泛应用于现代工业过程的故障检测中[2].PCA通过线性变换将原始空间划分为主元子空间(principal component subspace，PCS)和残差子空间(residual subspace，RS)，其中PCS包含原始数据的主要变化信息[3]. Hotelling’sT2和平方预测误差(square predicted error，SPE)两个统计量分别被用于监控样本在PCS和RS中的变化.由于T2计算时假设过程变量服从多元高斯分布，且不考虑样本间相关性，因此,PCA在实际工业过程的应用具有一定的局限性[4-5]. Ku等人在1995年针对过程动态性提出了动态主元分析 (dynamic PCA，DPCA)[6].DPCA通过引入时间序列增广数据矩阵，将过程中样本间的相关性转换为变量间的相关性，再利用PCA降维.与PCA相似，DPCA同样利用T2和SPE作为统计量进行故障检测，因此,DPCA在非线性或多模态过程中的应用具有一定的局限性[7].

针对工业过程数据的非线性和多模态特征，He等人于2007年提出了k近邻(k-nearest neighbor rule，kNN)故障检测方法.kNN方法在找到每个样本的k近邻之后，计算样本与其k近邻的距离之和，并以此作为统计量进行故障检测[8].kNN方法将近邻距离作为统计指标，不仅消除了过程数据的非线性和多模态特征，同时还消除了样本间的周期性(即动态性)[9].针对数据分布或变量关系的特征，许多学者提出了划分空间的思想理念.Ge等在2010年提出了一种基于线性子空间监控非线性过程的方法.该方法将原始数据经由PCA分解得到r+1个线性子空间，其中r为主元数[10].Tong等依据变量与PCS和RS的相关性，将原始数据分为4个子空间，分别进行检测[11].Huang等根据D检验，将观测变量分成高斯和非高斯两个子空间，分别运用PCA和ICA进行故障检测[12].但是，上述方法均没有考虑到PCA中潜隐变量自相关性对故障检测的影响.针对这个问题，本文提出了基于潜隐变量自相关性子空间划分的故障检测策略(fault detection strategy based on dividing autocorrelation of latent variables，FDDA).首先,应用PCA将原始数据分解为PCS和RS.其次，通过自相关系数将PCS分为显著自相关主元子空间(significant autocorrelation principal component subspace，SA-PCS)和微弱自相关主元子空间(weak autocorrelation principal component subspace，WA-PCS).RS被分为显著自相关残差子空间(significant autocorrelation residual subspace，SA-RS)和微弱自相关残差子空间(weak autocorrelation residual subspace，WA-RS).在SA-PCS和SA-RS中，选取kNN方法中的D2作为统计量对过程进行监控;同时，在WA-PCS和WA-RS中，分别应用统计量T2和SPE对过程进行监控.

1 算法简介

1.1 主元分析

原始数据X=[x1,x2,…,xn]∈Rm×n包含m个样本，n个观测变量.首先，应用Z-score对X进行标准化处理.接下来，应用PCA将X进行分解并获得相应的PCS和RS，如式(1)[13].

(1)

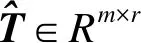
(2)

(3)

SPE=eeT.

(4)

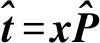
(5)

(6)

其中：T2近似服从自由度为r和m-r的F分布；SPE近似服从自由度为h的χ2分布[15-16].如果将训练数据SPE统计指标的均值和方差分别记为a和b，那么参数g=b/2a，同时h=2a2/b[17].α为置信水平，通常选取为0.99或0.95.此外，T2和SPE统计指标的控制限还可由核密度估计确定[18].

1.2 k近邻规则

k近邻规则是基于欧式距离来定义样本与其近邻.在故障检测领域中，如果测试样本与其近邻距离之和大于训练样本与其近邻距离之和，则判定该测试样本为故障[8].kNN算法首先在训练样本集中找出每个样本的前k个近邻样本.然后,利用样本与其k近邻样本的距离累计和D2作为统计指标进行故障检测，如式(7).

(7)

2 基于潜隐变量自相关性子空间划分的故障检测策略

2.1 序列自相关性划分

序列{xT}的均值函数为

(8)

其中:T为时刻;F(xT)为{xT}的分布函数[19].序列{xT}的自协方差函数定义为

Rs=E[(xT-μT)(xT-s-μT-s)],s=1,2,….

(9)

其中:s为滞后数;xT-s为T-s时刻的序列;μT-s为xT-s的均值.当s=0时，变量自协方差函数变为方差函数:

R0=E[(xT-μT)2].

(10)

由式(9)可知xT与xT-s存在线性依赖关系.当Rs>0时，xT与xT-s正相关；当Rs=0时，xT与xT-s不相关；当Rs<0时，xT与xT-s负相关.接下来引入自相关系数来表示变量前后相关性.

(11)

当s=0时，ρ0=1.一般的，ρ0取值分为4个区间:|ρk|∈[0,0.3]为微相关；|ρk|∈(0.3,0.5]为实相关；|ρk|∈(0.5,0.8]为显著相关；|ρk|∈(0.8,1]为高度相关[20].

2.2 基于潜隐变量自相关性子空间划分的故障检测策略

传统PCA、DPCA等方法没有考虑潜引变量自相关性，这将导致故障被误判为正常[21].针对潜隐变量自相关性的判别及划分，提出基于潜隐变量自相关性子空间划分的故障检测策略.FDDA方法主要包含两个阶段：离线建模和在线监测.

2.2.1 离线建模

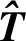
2.2.2 在线监测

对于测试样本x*

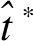
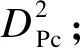
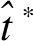
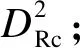
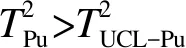
3 TE过程

TE过程是由位于田纳西州的伊斯曼化工公司提供的真实工业过程仿真模型.它被广泛应用于评价过程监控及诊断方法的有效性[22].TE过程包括5个主要单元：反应器，冷凝器，压缩机，分离器，汽提塔.整个过程包含22个连续测量变量、11个操纵变量和19个成分测量值.

采用TE过程生产模式1的数据进行仿真实验.训练数据和测试数据各包含960个观测值和52个变量，在此过程中共有21类故障，故障均在第161时刻引入[23].使用FDDA、PCA、DPCA和kNN方法对TE过程的故障进行检测.其中FDDA、PCA及DPCA主元数为17，DPCA中由交叉验证得知滞后数L=2可以提取过程所有线性关系[6].kNN中k近邻数由寻优测试确定为3.控制限均采用99 %.表1为PCA、DPCA、kNN及FDDA对21种故障的检测率(fault detection rate，FDR)和误报率(fault alarm rate，FAR)，其中最高检测率和最高误报率已作加粗处理.

表1 TE过程检测率和误报率Table 1 Fault detection rate and fault alarm rate of TE process

传统基于PCA的方法对故障3(物料D的温度发生变化，类型为阶跃)、9(物料D的温度发生变化，类型为随机变量)、15(冷凝器冷却水阀门，类型为阀黏滞)检测困难[24]，因此对这3个故障不作讨论.传统方法对故障5、10、16均有较大的漏报率.由表1可知:FDDA在大尺度故障检测率高的基础上，也提升了对故障5、10、16等小尺度故障的检测率.

以故障5为例进行分析.故障5是冷凝器冷却水入口温度引入阶跃变化所导致，从而得分变量44～50有较为明显的异常变化.PCA、DPCA、kNN的故障5检测率见表1.图1是FDDA在4个子空间的检测图.综合以上检测结果可以发现，FDDA方法具有较高的故障检测率.由于PCA和DPCA方法没有考虑到得分变量的自相关性，因此,相应的T2和SPE控制图具有较低的故障检测率.虽然kNN方法直接监控过程变量，但kNN通过计算欧式距离选取近邻的方式在一定程度上不考虑样本间的周期性，其对于与训练样本边缘点很近的故障检测效果不佳[25].

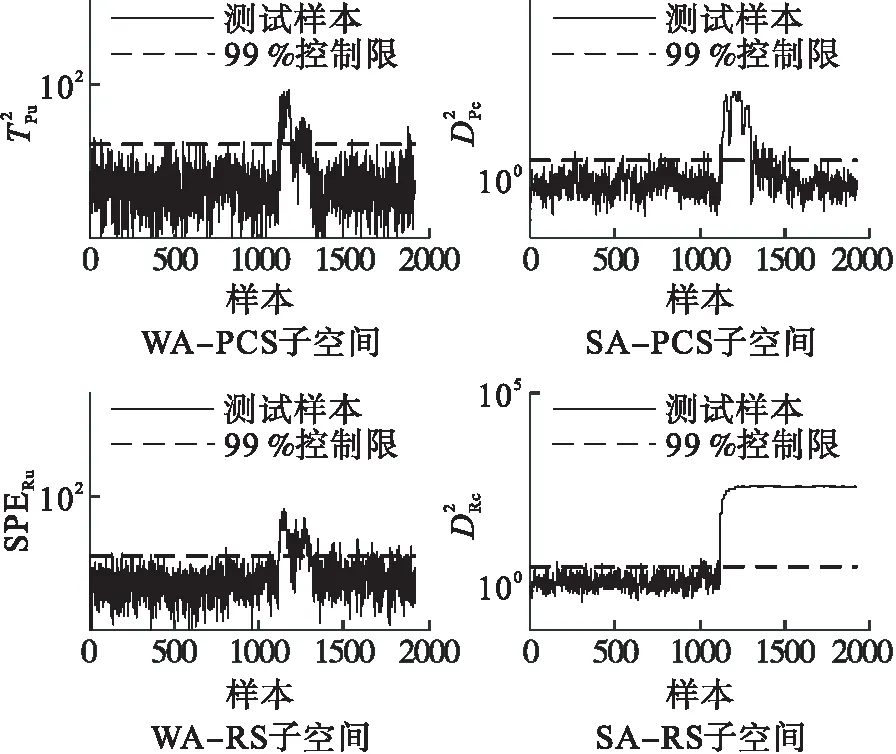
图1 FDDA在4个子空间的检测结果Fig.1 FDDA detection results in four subspaces

为验证将得分变量自相关性作为划分依据的有效性，依据观测变量自相关性对输入空间进行了空间划分：将显著及高度自相关变量纳入显著自相关性子空间(significant autocorrelation subspace，SAS)，利用kNN进行检测；其余变量纳入微弱自相关性子空间(weak autocorrelation subspace，WAS)，利用PCA进行检测.如图2所示,检测率仍然低于FDDA方法.实验结果进一步说明FDDA方法的有效性.

在FDDA方法中，在SA-RS子空间运用kNN方法成功检测出故障5，因此,本节也在RS中直接应用kNN对故障5进行检测，结果如图3所示.通过PCA选取17个主元，此时残差子空间包含35个变量.由于故障发生在方差较小的得分且各得分的自相关性不同(图4是第49个得分变量的自相关性图，可知经过投影后的得分变量自相关性较高)，该特点导致kNN方法具有较低的故障检测率.

(a) PCA在WAS子空间 (b) kNN在SAS子空间图2 观测变量自相关性划分子空间检测结果Fig.2 Fault detection results in subspace divided by observed variable autocorrelation

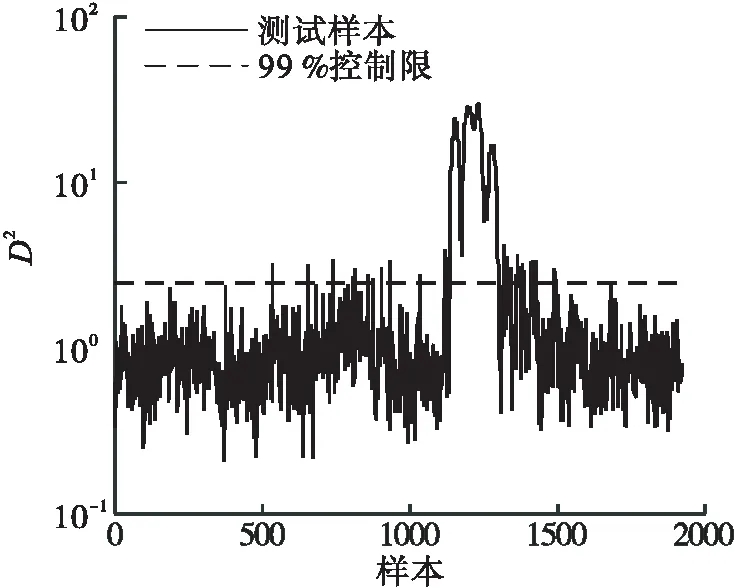
图3 kNN在残差子空间检测结果Fig.3 Fault detection results using kNN in RS

图4 第49个得分变量自相关性Fig.4 Autocorrelation of the 49th score variable

4 半导体蚀刻工艺

半导体数据集采自德克萨斯州仪器公司的半导体蚀刻过程[26].数据集包含3个实验过程中的108个正常晶片，21个故障晶片.由于正常晶片和故障晶片各有1个批次数据缺失严重，因此只采用107个正常晶片和20个故障晶片.在正常晶片中随机挑选11个晶片作为校验数据，其余作为训练数据建模[27].采用基于统计模量的批次数据处理方法，数据集包含68个监控变量[28].

将PCA、DPCA、kNN与FDDA进行比较分析，PCA、DPCA、kNN及FDDA检测率见表2.PCA在PCS中检测出4个故障批次，在RS中检测出16个故障批次.DPCA在主元子空间和残差子空间分别检测出4个和19个故障批次.由于半导体是典型的多工况、多阶段、非线性生产过程[28]，上述特征导致基于PCA方法的检测具有较低的故障检测率.kNN中近邻数k选取为3，有5个故障批次未被检出.kNN搜索全局近邻，易受离群点的影响，导致控制限设定较高.另外，由于某些故障尺度较小，因此故障未被全部检出.FDDA在WA-RS子空间的检测结果如图5所示，20个故障批次全部被检出.FDDA中主元数为14，WA-PCS子空间有8个得分变量，SA-PCS子空间有6个得分变量(为第1/2/3/4/5/9个得分变量)，WA-RS子空间有49个得分变量，SA-RS子空间有5个得分变量(为第15/18/32/44/67个得分变量).在RS中直接应用SPE进行故障检测，检测结果如图6所示.由图7可知，由于RS中的部分变量存在自相关性，不符合SPE统计量的假设条件，导致故障在RS中未被全部检测出来.

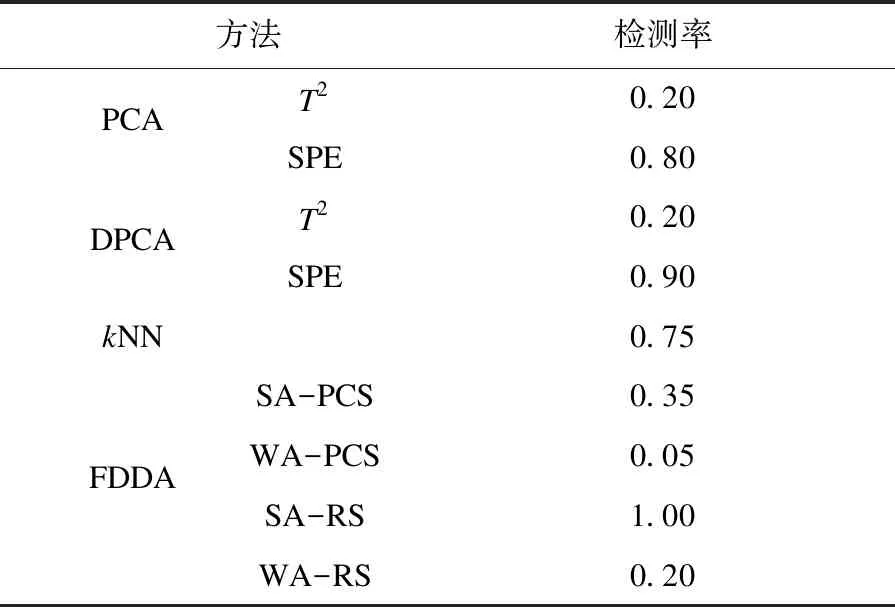
表2 半导体蚀刻过程检测率Table 2 Fault detection rate of semiconductor etching process

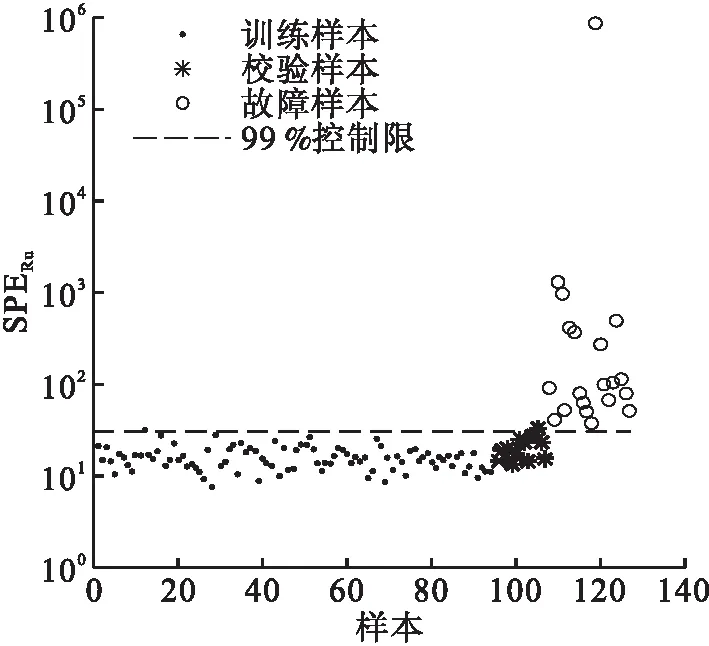
图5 FDDA在WA-RS检测结果Fig.5 Fault detection results using FDDA in WA-RS

图6 PCA在RS检测结果Fig.6 Fault detection results using PCA in RS

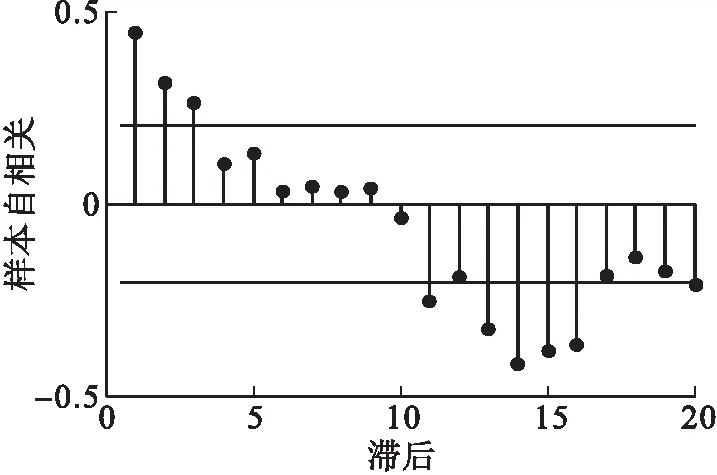
图7 RS中变量8自相关性Fig.7 Autocorrelation of the 8th variable in RS

为了对比FDDA方法的有效性，在观测变量上依据自相关性进行空间划分：显著自相关性子空间和微弱自相关性子空间，分别用kNN和PCA进行检测，结果如图8所示.由图8可以看出：直接依据自相关性划分空间的方法并没有提高故障检测率.该结果说明，FDDA的空间二次划分方法能够准确分离故障，提高过程的故障检测率.

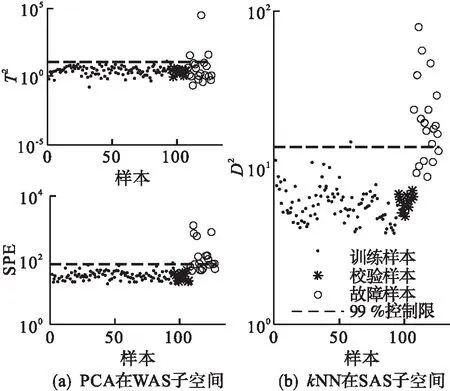
图8 观测变量自相关性划分子空间检测结果Fig.8 Fault detection results in subspace divided by observed variable autocorrelation

5 结 语

针对工业过程潜隐变量自相关性的问题，提出了基于潜隐变量自相关性子空间划分的故障检测策略.首先，通过PCA将原始输入空间分为PCS和RS；其次，根据得分变量自相关性对上述空间进行二次划分；最后，对4个子空间进行联合监控.该方法不仅能够处理变量间相关性，同时还能够捕获得分变量自相关性.通过TE过程和半导体蚀刻过程的仿真实验，同时与PCA、DPCA、kNN的故障检测率进行对比，验证了FDDA方法对动态过程故障检测的优越性.

由于FDDA方法在检测过程中多次使用寻优测试确定近邻数k，因此，近邻数k的确定方法是接下来的研究方向.