无混载校车路线分析模型优化实现方法

高 巍，陈泽颖，李大舟

(沈阳化工大学 计算机科学与技术学院， 辽宁 沈阳 110142)

随着中国社会经济不断发展，义务教育的发展面临新的任务和要求，从21世纪初开始，为降低学校的运营成本，优化教育资源配置，促进教育均衡发展，我国进行了大规模的学校重新布局调整和撤并.学校的布局调整解决了班级规模和教育资源浪费的问题，但却引发了一个新的问题：学生入学距离的增加和上下学的不便. 近年来，为方便学生上下学，对中小学生校车服务的需求日益突出，不少地区开始逐渐开展校车服务.规划一组校车路过学生人数已知的站点，早上将学生从居住地附近送达学校，下午接他们送回[1].对这些车辆的路径规划称为校车路径问题(SBRP)[2],校车不仅可以很大程度上提高道路利用率，而且还能节省大量的能源.

在校车运营中存在许多不合理的校车路线设计及校车运营方式，缺乏路径规划优化的经验.目前大多数校车运营在校车安排上依靠简单的人工规划路径，调度过程困难且调度结果缺乏模型理论的支持，造成校车资源浪费、校车行驶总路程过长等问题；学生乘坐校车的费用增加，对社会资源亦造成一种浪费，且校车乘车服务质量不高[3].

文献[4-9]针对单校车问题分别给出了求解算法.Zhang 和 Li使用量子粒子群算法(quantum-behaved particle swarm optimization，QPSO)解决了甘肃民族师范学院教职工校车路径问题[4].Euchi和Mraihi结合蚁群算法(ant colony optimization，ACO) 与 变 邻 域 搜 索 算 法 (variable neighborhood search，VNS)提出了一种混合算法[5].刘青松采用元启发式框架,在校车不超载的约束下,用车辆的行驶距离之和最小作为优化目标,规划出校车的数目[6].张富和朱泰英在学生乘车站点设计方面提出双目标非线性规划模型，运用了相应启发式优化算法[7].刘青松等将单校校车路径问题抽象化为开放式车辆路径问题，以车辆载荷为约束条件的基础上，实现车辆行驶距离最短的优化目标，其求解结论明显优于Arc GIS[8].吕腾捷[9]主要实现了最优站点的选择、最优路径的规划及成本效益分析.本文以最短路径为目标函数建立一个快速有效的无混载校车路线分析模型，求出一条满足所有约束条件的路径，达到降低校车运营成本的目的.

1 上下学时校车的最短行驶路径问题

1.1 乘降站位置选择

乘降站位置选择应考虑约束条件包括学生步行距离，学生上下车方便安全，校车运营成本等，对乘车站点的选择将间接影响校车运输成本控制和服务质量,从而影响对站点和路径的决策[10].

考虑到学生上下车方便，校车停车点与所接学生家庭住址距离在500 m以内，考虑最经济、最快速的路线和停车点安排.假设学校U有S个学生，S个学生有S个经纬度坐标.以S个经纬度坐标为圆心，500 m为半径画圆，有500个圆，将多个圆的重叠区域设为乘降站选址的可行区域.有的圆没有与其他圆相重叠的区域，将该圆的整个圆区域设为乘降站选址的可行区域.在乘降站选址的可行区域内根据实际周边环境选择停车安全、道路较为宽敞、距离十字路口较近的地点作为乘降站具体地点，如图1所示.

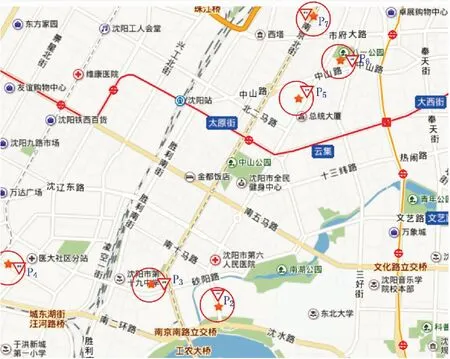
图1 乘降站位置选择Fig.1 Pick up and drop station location selection

使用上述乘降站位置计算方法，U学校的S个学生需要在m个乘降站下车回家.m个乘降站的编号P1，P2，P3，…，Pi，…，Pm-1，Pm.以U校为例，图1中共有7个乘降点，编号为P1，P2，P3,…，P7.

1.2 上下学时校车的最短行驶路径问题

1.2.1 问题定义

最短路径问题用于计算一个节点到其他所有节点的最短路径.上学时校车的最短行驶路径问题就是从出发点开始，经过所有乘降点最终到达学校的最短路径；放学时将所有学生送到对应的乘降点的最短路径.最短路径算法是解决在具有拓扑关系的连通网络中找到两点之间最优路径问题的有效方法，它除了能够计算最短路径距离外，还能通过给每条边赋不同的权重值来满足不同的搜索条件，如耗时最少路径[11-13].

1.2.2 问题描述

分两种情况描述最优路径问题：极限情况和一般情况.

极限情况：U学校有S辆校车，要完成送S个学生上学.极限情况下每个学生都会独自乘坐一辆校车，从家附近的乘降站直接到达学校，中途无需经过任何其他乘降站，所走的路径就是学校到该学生家之间的最短路径，使用经典最短路径算法(算法A)就可以求出该路径.

一般情况：U学校有n辆校车，要完成送S个学生上学.追求在n辆校车中行驶距离最远的校车的行驶距离最短.该情况是在充分利用现有校车资源的情况下，追求每个学生尽快到达学校的校车行驶路线.

一般情况的最优解就是极限情况中所描述的答案.每个学生自己单独乘坐一辆校车，不和其他同学共用校车.此时需要m辆校车分别从m个乘降站出发直接到达学校，该方案中行驶距离最远的校车的行驶距离等于距离学校最远的乘降站与学校之间的距离.

现在开始削减校车数量，同时保证所有校车中行驶距离最远的校车的行驶距离最短.校车数量从m辆减为m-1辆.此情况下，原来到达某个乘降站的校车被取消，该校车上的学生要和到达其他乘降站的学生合并乘坐一辆校车.

假设m辆校车C1，C2，C3，…，Cm中校车Ci被取消，校车Ci中的学生改为乘坐校车Cj.根据以下方法在剩余的m-1辆校车中选择校车Cj：分别把原来校车Ci中的学生放到剩余的每一辆校车中，获得m-1辆校车的新的m-1个行驶路线.选择新的m-1辆校车行驶路线中变化后行驶距离最小的那辆校车作为校车Cj，让校车Ci的学生改乘校车Cj.该方案就是m-1辆校车到达m乘降站时，保证行驶距离最远的校车的行驶距离最短.

根据上述方法可以获得在保证所有校车中行驶距离最远的校车的行驶距离最短条件下，m-1辆校车到达m乘降站的最优方案.每削减1辆校车后的最优方案都是在当前最优方案基础上实现的，该问题的最优解包含了子问题的最优解，因此该问题具有最优子结构.问题的最优子结构特征是该问题可以采用上述动态规化算法(算法B)求解的保证.

1.3 问题的算法设计

1.3.1 算法A

算法A用来确定地图上任意两点之间的最短路径，并且该路径不必经过其他特定位置上的点.在寻找两个乘降站之间的地图最短路径，或者寻找一个乘降站和一所学校之间的地图最短路径时都会使用算法A.

算法A基于图论，乘降站、学校和地图上十字路口都被视为一个图G的顶点V.连接乘降站、学校和地图上十字路口的道路被看成是该图G的边E.每条边无方向但是有权重W，权重W就是该路径的长度.该图G上只有相邻的两个顶点V有边E，地理因素决定不是所有顶点V都是相邻顶点，例如：不是所有的十字路口之间都有直接道路相连，如图2所示.

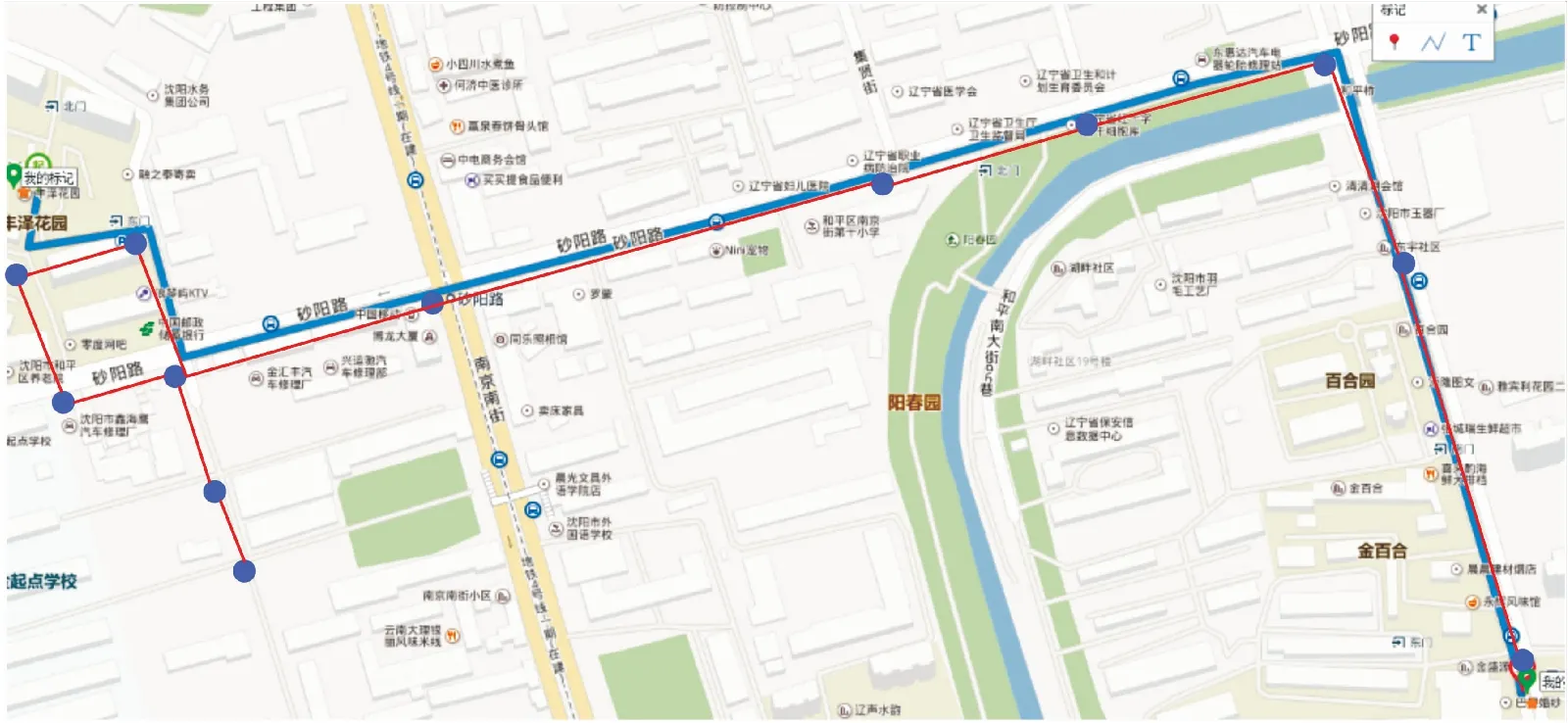
图2 两个乘降站之间的最短路径Fig.2 Shortest path between two boarding stations

综上图G可以看成是一个无向有权半连通图，算法A就是在图G中找到任意两定点V之间的最短路径，该路径无需经过特定顶点[14].该问题有很多经典算法可以求解，这里采用Dijkstra算法求解.Dijkstra算法的思想是从起点遍历与其相邻的节点，找到最短距离的点，标记该点，然后遍历新点相邻且未标记的点，重复之前的搜索计算步骤，直到目标点被标记，即从起点到目标点的最短路径[15-16].

1.3.2 算法B

算法B主要解决的问题是在m辆校车中选择一辆校车Ci作为被取消的校车，校车Ci可能是原来m辆校车中的任何一辆，因此校车Ci的选择要遍历所有m辆校车，即把每一辆校车作为Ci来计算一次，该过程可以以每个校车都是Ci为对象.

在计算m-1辆校车因为承担运送校车Ci中学生而产生行驶路线发生变化后的最短行驶距离时，针对m-1辆校车中每一辆校车使用最短路径搜索算法.对于承担任务的m-1辆校车中的任意一辆校车，以学校为源点，找到途经2个乘降站(该校车原来的目的乘降站、车校Ci的乘降站)的最短路径，并把该路径距离作为该校车承担运送校车Ci中学生而产生行驶路线发生变化后的最短行驶距离.

校车Ci可能是任意一辆校车，每一校车都作为Ci进行计算一次，找到结果Cj和对应的新的Cj最短行驶距离.在m个方案比较新的Cj最短行驶距离，确定最优方案时Ci的选择，并将该方案中的Cj作为最终结果.

综上，如果想获得m-2辆校车到达m乘降站的最优方案，可在m-1辆校车到达m乘降站的最优方案基础上，再次使用上述方法，即可获得保证所有校车中行驶距离最远的校车的行驶距离最短条件下，m-2辆校车到达m乘降站的最优方案.

使用m-n次该算法，直到校车数量从m被减为n为止.此时就是保证在n辆校车中行驶距离最远的校车的行驶距离最短，安排n辆校车中每辆学生的人数，以及确定哪位学生乘坐哪辆校车的最优解.

以此类推，每削减一辆校车后的最优方案都是在当前最优方案基础上实现的，该问题的最优解包含了子问题的最优解，因此该问题具有最优子结构，可采用动态规化算法.算法B因此基于动态规划技术.

算法B将m-n辆校车分担m个接送任务拆分成m-n次，其中第i次是对m-i由m-i-1的寻优，即每一次的寻优都是在前一次寻优基础上进行的，而且每一次寻优的计算方法都是相同的.

算法B把多阶段过程转化为一系列单阶段问题，逐个求解，抽象其中单次寻优过程.

2 实 验

2.1 实验数据

以SY市某校U为例，该校位于SY市，学生数据为就读于该校附近的学生信息.所获得的数据信息整理为Excel数据(见表1)，包括10个属性，学生ID(5位数字)、就读学校名称(U校)、年级、班级、性别(0～1)、出行方式、上学离家时间、乘校车意愿(0～1)和家庭住址.其中乘校车意愿属性中0表示不愿意乘坐校车，1表示愿意乘坐校车.家庭住址标属的标准格式为xx区xx街xx号，以提供坐标轴，获得精准的经纬度坐标.

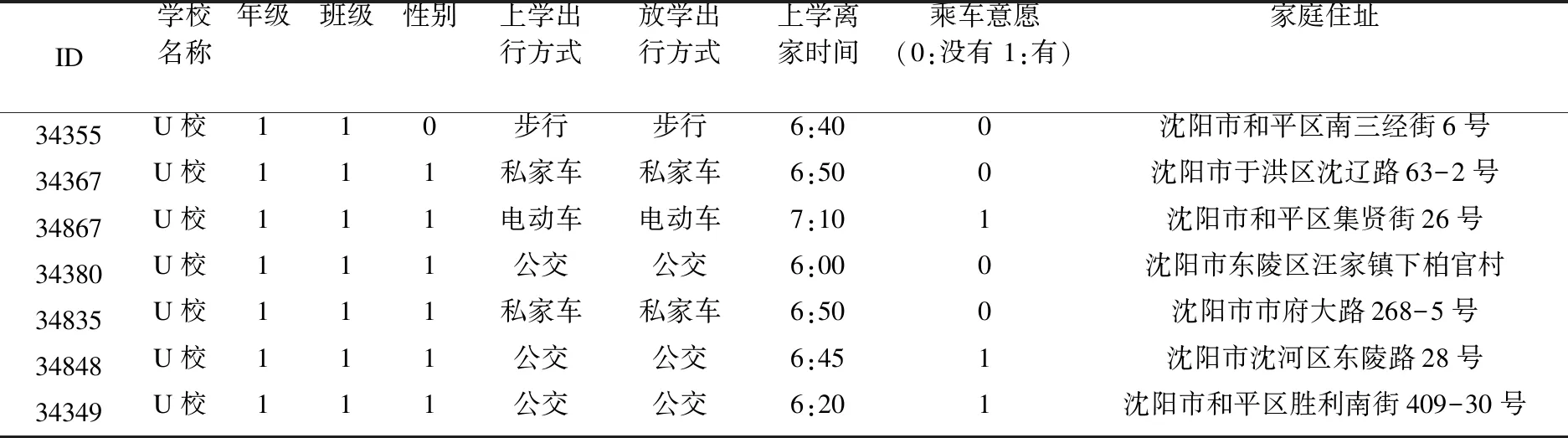
表1 U校学生信息表Table 1 Student Information of U school

2.2 实验结果分析

2.2.1 算法A

算法A以U校为例，选取其中任意一个愿意乘坐校车的学生，学生家为起点，学校为终点，利用算法A计算从学生家到学校的距离和时间(见图3).利用算法A可以计算各乘降点之间和各乘降点到学校的距离，为下一步的路径规划提供有效的数据帮助.

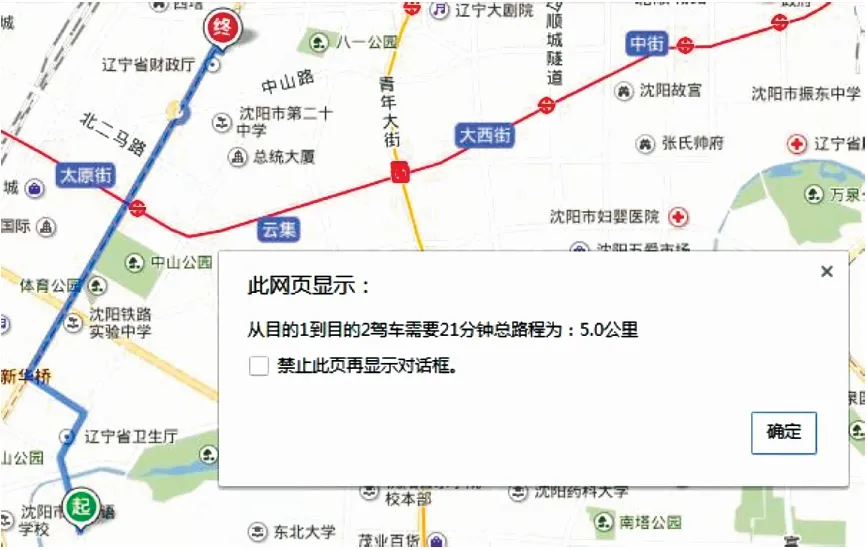
图3 算法A计算两点的最短距离Fig.3 Algorithm A calculates the shortest distance between two points

2.2.2 算法B

U学校有7个学生通过校车上学和放学，该7位学生住的比较分散，每个学生都有一个独立的乘降站.在图4中给出了U学校的位置和7个乘降站的位置P1，P2，P3，P4，P5，P6，P7.

图4 U学校的7个乘降站分布Fig.4 Distribution of 7 boarding stations in U school

下面以放学为例，上学问题是放学问题的等价反问题，因此可以采用相同的解法.为让每一个学生都能尽快回家，极限情况下是每个乘降站都有一个校车直接到达.因此最优情况是7辆校车C1，C2，C3，C4，C5，C6，C7分别从学校直接到达7个乘降站P1，P2，P3，P4，P5，P6，P7.为了节约校车运营成本，增加校车的运载率，假设学校希望从7辆校车减少为4辆校车，则需要通过算法B运算3次，每一次都选择出取消哪辆校车Ci是最优的，同时从剩下的校车选择出最优的校车Cj来完成被取消的校车Ci的任务.

下面以第1次执行算法B为例，校车数量从7辆削减到6辆，算法执行完后能够判断出被取消的校车Ci和代替Ci完成到达乘降站Pi任务的校车Cj.

首先，列出U学校以及7个乘降站相互之间的最短距离，可以采用算法A来实现表中每项数值的获得，如表2所示.

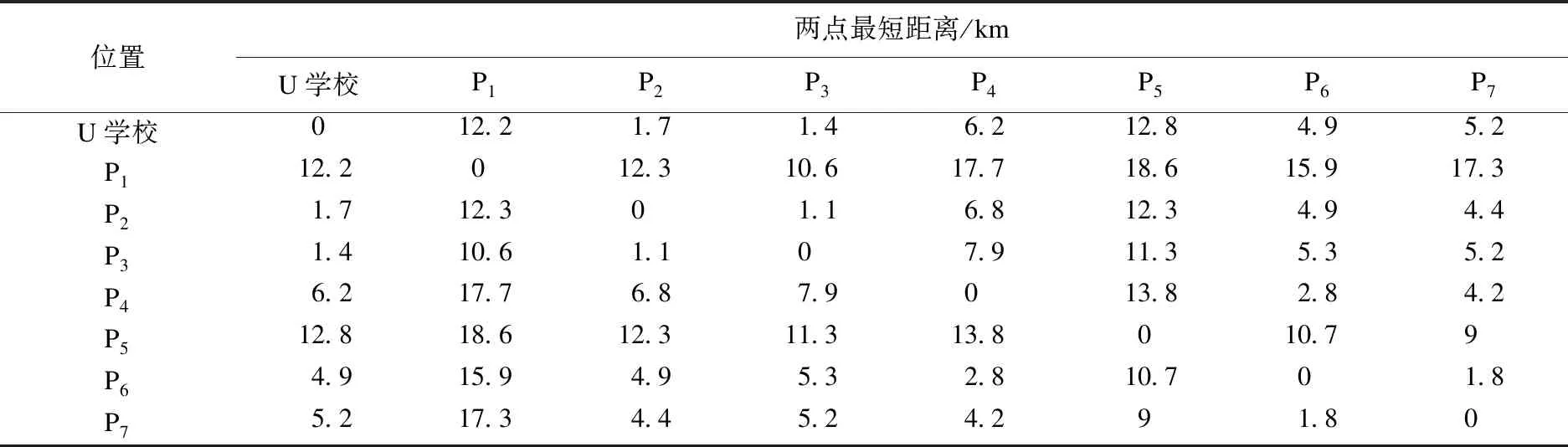
表2 U学校以及7个乘降站相互之间的最短距离Table 2 The shortest distance between U school and 7 boarding stations km

分别将每个校车都作为Ci和Cj进行考虑，计算出每种情况下，行驶最远的校车的行驶距离.例如：当C1=Ci，C2=Cj时，校车C2除了要到乘降站P2之外，还要到乘降站P1.校车C2新的最短行驶路线长度和最短行驶路线可以根据下面提到的算法获得，路线是U学校→P2→P1，最短长度是1.7+12.3=14 km.该情况下，6辆校车中行驶最远的校车就是校车C2，其最远行驶距离是14 km.当Cx=Ci，Cy=Cj时，方案中最短行驶距离Px到Py的最短距离+Min{U学校到Px的最短距离，U学校到Py的最短距离}.

根据此算法得出表3中每一个表项数值.该表中每一数值表示校车Cj由于接替了Ci的任务而生成的新的最短路径长度.

表3 校车Cj由于接替了Ci的任务而生成的新的最短路径的长度Table 3 Length of the new shortest path generated by the school bus Cj to take over the task of Ci km

新方案共有42种，每种新方案都会删除校车Ci的原有行驶距离，增加校车Cj的原有行驶距离.

综合考虑42种新方案中每一种方案行驶最远的校车的行驶距离是多少.例如：当C1=Ci，C2=Cj时， 该新方案行驶最远的校车的行驶距离可以根据表4直接找出.

表4 C1=Ci，C2=Cj时，该新方案行驶最远的 校车的行驶距离Table 4 When C1=Ci,C2=Cj,the travel distance of the school bus with the farthest travel of the new scheme

结果是C1=Ci，C2=Cj时，该新方案行驶最远的校车的行驶距离等于14 km.

当Cx=Ci，Cy=Cj时，方案中行驶最远的校车的行驶距离=Max{Px到Py的最短距离+Min{U学校到Px的最短距离，U学校到Py的最短距离}，Max{7个乘降站之间的相互距离}}.

根据此算法得出表5中每一个表项数值.该表中每一数值表示该新方案行驶最远的校车的行驶距离.

由表5可知：新方案行驶最远的校车的行驶距离在表中的每一项里给出，其中数值最小的是12.2 km.因此，取消校车C5，让校车C7代替C5到达乘降站P5是最优的从7辆校车减为6辆校车的方案.

采用同样的方法，可以计算出从6辆校车减为5辆校车的最优方案.依次类推，反复使用算法B，最终可以得到U学校具有4辆校车时，最优的学生乘坐分配方案.

需要注意的一点是如果方案中最优的方案不止一种时，要根据前一个表，选择校车Cj由于接替了Ci的任务而生成的新的最短路径长度最小的方案.该方案表明在行驶最远的校车的行驶距离最小的条件下，原来乘坐Ci和Cj到达乘降站Pi和Pj的学生所受到的影响也被降为最低.

3 总 结

本文就校车路径规划问题，查阅相关学校的上学放学时间，充分调研各个学生的家庭住址和SY市交通情况，综合考虑校车运营方式和盈利方法，对实际的校车运营问题进行分析，提出了算法，实验结果表明运用算法后的行车距离更短，校车数量减少，运营成本降低，达到预期效果.

本次建模以完成接送每个学生上学放学为要求，以盈利最大化为最终约束，提出算法.首先，通过对每个学生家庭住址的研究，利用网络地图对他们的地址进行精确定位.之后将所有的地址信息抽象成乘降站，充分利用算法A计算各乘降点之间和各乘降点与学校的距离，然后利用算法B进行一系列复杂的计算，并最终获得了单校校车情况下最佳的校车路线、最佳数量.

本文在建立校车线路优化模型时没有考虑城市交通情况. 实际上，校车的运行时间集中在早晚的城市交通高峰期，不可避免地导致交通拥堵和校车不及时现象. 在这个阶段，由于这种情况，部分学校提前或推迟上下学时间，学校在设计校车路线时应考虑这个因素，这时路径最短便不是最优结果. 因此，如何设计规划校车线路和乘降站，如何合理运营校车实现最大经济效益是目前研究的重点[17].