矩阵Hadamard积最小特征值下界的进一步估计

周 平 李艳艳 蒋建新

（文山学院数学与工程学院 云南文山 663099）

一、引言

M-矩阵是一类在数值代数研究中具有广泛应用的矩阵，在管理科学、物理学、图论、生物学、经济学等领域的许多问题都与它有关[1,2]。而矩阵的Hadamard积是一种特殊的矩阵乘积，它也被广泛的应用于对概率论中特征函数的研究,量子计算、通信中的编码理论、区组设计等问题，基于这些重要的应用背景，M-矩阵Hadamard积的最小特征值下界问题一直受到很多学者研究的热点之一[3-9]，其中在文献[3]中给出了如下估计式：

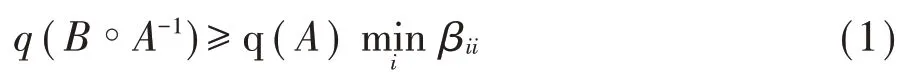
本文对M-矩阵的Hadamard积最小特征值下界作了进一步估计，并给出两个改进了已有的一些结果的新估计式。

二、符号、定义和引理

记Cn×n（Rn×n）表示所有n×n阶复（实）矩阵构成的集合为矩阵A的谱半径，σ(A)为A的谱[1,2]。

设A=(aij)∈Rn×n，i,j,k∈N，i≠j，令：

设A∈Mn，D=diag(d1,d2,…,dn)，di＞0(i=1,2,…,n)，使得D-1AD是行严格对角占优M-矩阵[3-5]。

若A=(aij)∈Cm×n,B=(bij)∈Cm×n,用A◦B表示A与B的对应元素相乘而得到的m×n阵,即

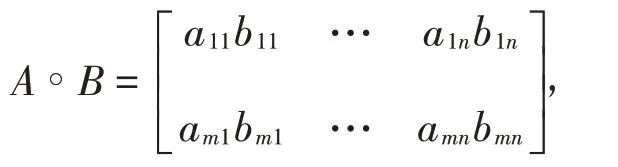
称其为A和B的Schur积,也称为Hadamard积[6-8]。

若A=(aij)∈Zn×n,则称q(A)=min{Re(λ)|λ∈σ(A)}为A的最小特征值[8]。

若A∈Mn,则q(A)为A的模的最小特征值,且q(A)=

引理1[3]如果A=(aij)∈Cn×n,0≤α≤1，而且xi∈R(xi＞0)，那么A的所有特征值包含在下列集合中：

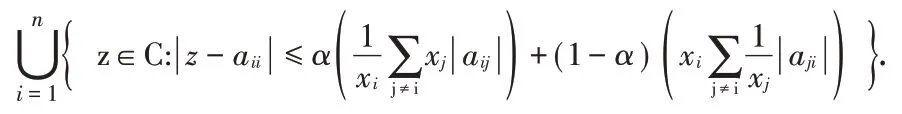
引理2[4]设A,B∈Rn×n都为M-矩阵且B非奇异,则A◦B-1为M-矩阵。

引理3[5,6]设A,B∈Rn×n,且D,E∈Rn×n是对角矩阵，则

引理4[7]设A=(aij)∈Rn×n是一个行严格对角占优M-矩阵，则A-1=(βij)存在，且有

引理5[8]如果是一个行严格对角占优-矩阵,那么A-1=(βij)存在，且有

三、q(B◦A-1)和q(A◦A-1)的新估计式

定理1 设A=(aij),B=(bij)∈Mn，A-1=(βij)，则q(B◦A-1)的下界为

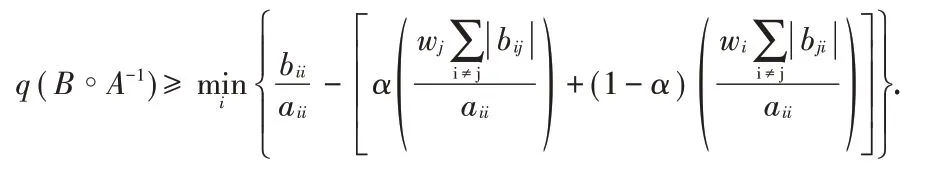
证明 已知A=(aij),B=(bij)∈Mn，则运用引理2和3可得

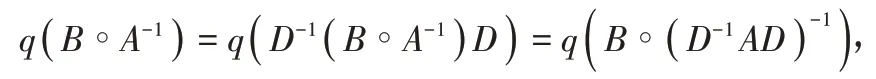
这里D=diag(d1,d2,…,dn)，di＞0(i=1,2,…,n)，D-1AD是严格对角占优M-矩阵。

为了不失一般性，现假设A是严格行对角占优M-矩阵，下面分两种情况进行讨论：

Ι)如果矩阵A和B都是不可约矩阵时，令则

因此，存在实数θji(0≤θji≤1)，使得

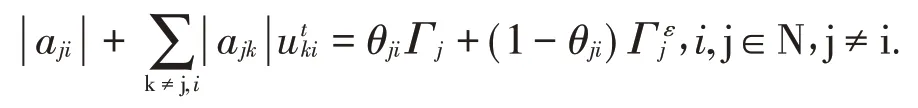
由文献[2]中的定理3.1知0＜wj≤1。设则根据引理1知，存在i0∈N，使得

由引理5，上式可转化为

故

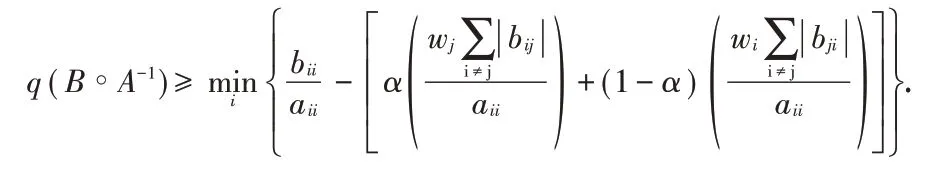
Π)如果A和B中至少有一个是可约矩阵时，令G=(gij)是n阶置换矩阵，此矩阵中g12=g23=…=gn-1,n=gn1=1，其他的gij=0，对充分小的正数η，能够使得A+ηG,B+ηG的所有主子式都是正的，从而A+ηG,B+ηG∈Mn此时用A+ηG，与B+ηG分别替代A,B，当η→0时，综合Ι)的证明和连续性知结论仍然成立。

注1：在定理1中令α等于0可得

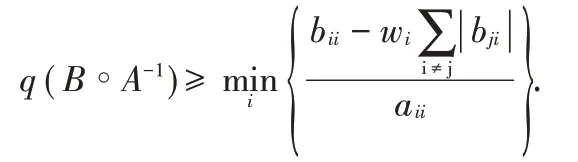
即为文献[9]中获得的(4)式，因此文献[9]中给出的估计式包含于本文给出的定理1。

推论1 设A=(aij),B=(bij)∈Mn，且A-1=(βij)，当时，则有

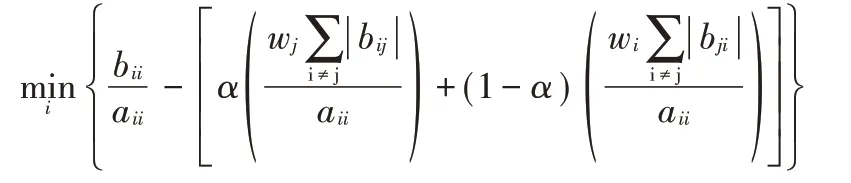
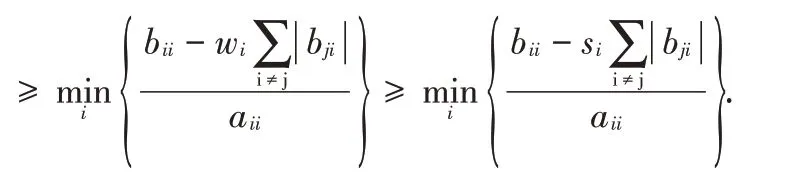
证明 由于

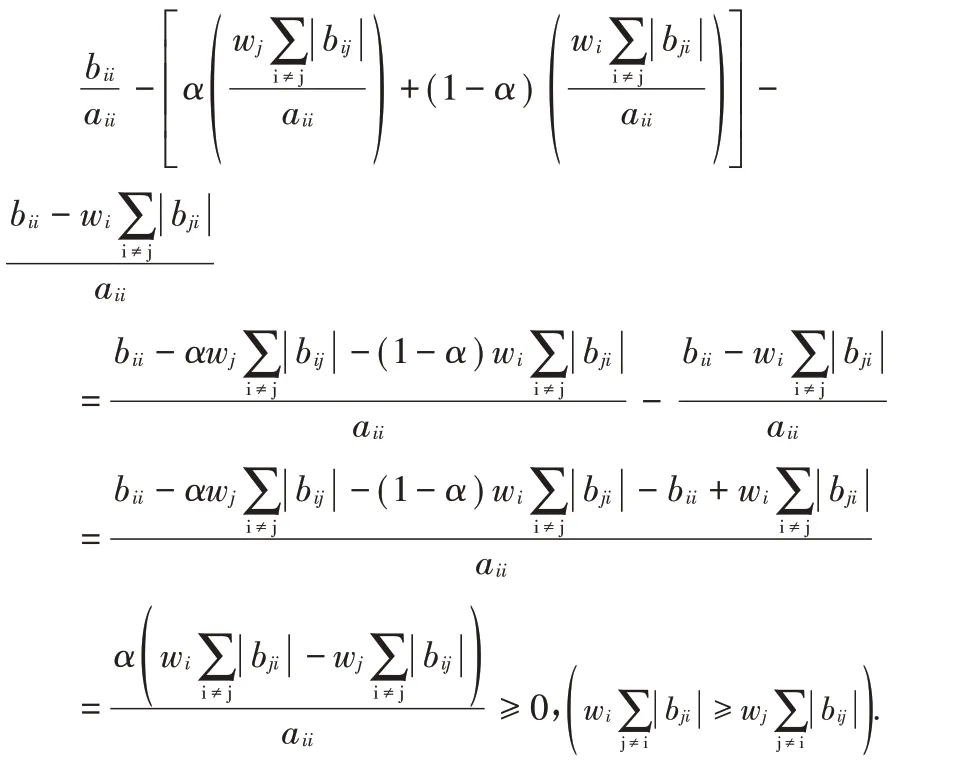
所以

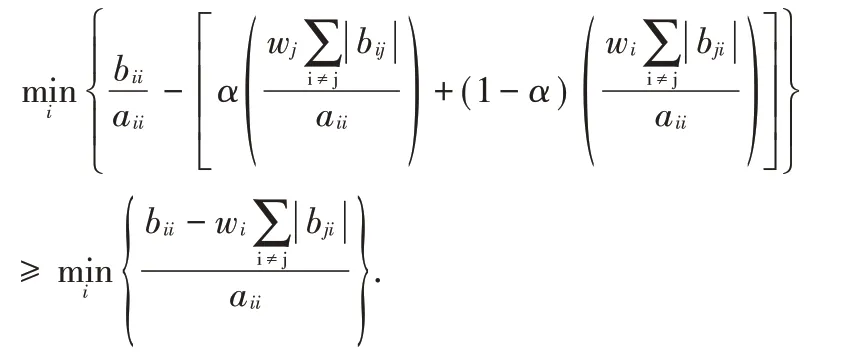
由wi和si的定义知，si≥wi，从而

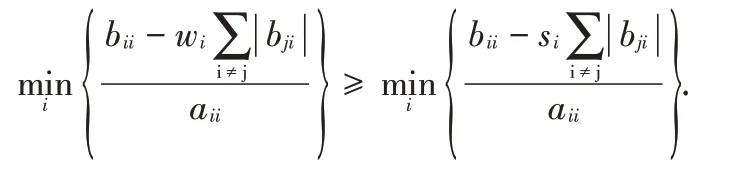
故综上所述，得

注2：根据注释1和推论1的证明可知定理1给出的估计式比已有文献[6]和[9]的结果更优。

如果A与B是两个相同的非奇异M-矩阵时，那么可以得到如下结果：

定理2 设A=B=(aij)∈Mn，A-1=(βij),则

注3：在定理2中令α等于0可得

即为谭学文等[9]获得的(5)式，因此文献中给出的估计式包含于本文给出的定理。

同理应用推论1可得到如下结论：

推论2 设A=B=(aij)∈Mn，A-1=(βij),则

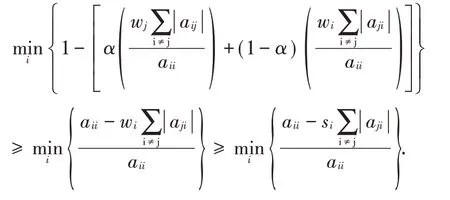
注4：根据注释3和推论2的证明可知定理1给出的估计式比已有文献[6]和[9]的结果更优。

四、结语

根据注释1-4可知，文中给出的估计式改进了已有文献[5]，[6]和[9]的结果，是对M-矩阵的Hadamard积最小特征值下界方面研究的一个有益的补充。