利用“SAS”管探数学建模思想应用

文/清远市清城中学

在初中数学教学中，利用数学建模思想，可以培养学生的思维意识和思维方向，可以培养初中生数学归纳能力、理解能力、关联能力和创新应用能力。下面我们以全等三角形判定定理“SAS”为例，管探数学建模思想的应用。

一、利用“SAS”培养思维意识、构建数学模型

数学模型是相对于原型而言的，是对数学原型进行的一种抽象和概括。找出其规律特性，找出其不变的、可应用的、相对固定的数学关系。在初中证明三角形全等时，有一个判定定理“SAS”，通过“SAS”的应用，可以培养学生的思维意识，构建新的数学模型。

例1.在△ABC中，AB=AC，点E、F分别在AB、AC上，且BE=FC，求证：△ABF≌△ACE。

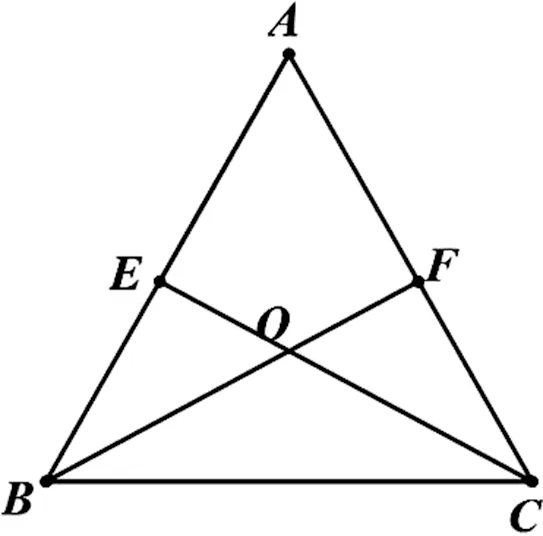
图1

分析：从分析△ABF与△ACE全等现有条件和所需条件着手。引导学生寻找已知条件：AB=AC，∠BAF=∠CAE。所需条件：①另外两角中任意一角相等；②AE=AF。

关联已知条件：BE=CF，即可发现AE=AF。从而成功关联到原型“SAS”上，解决了问题。

归纳：①两个三角形有一个公共顶点；②从公共顶点引出的两组对应边也相等；③以两个三角形的公共顶点为顶点的对应角相等。

这样就以“SAS”为原型完成了一个新的数学模型的构建。(也可称之为“手拉手模型”)

二、利用数学模型，培养思维能力，实现快速解题

在教学中，教师要善于引导学生养成数学建模意识，且充分利用模型思想准确、快捷解决问题。

例2.以△ABC的两边AB、AC分别为边作正△ABD、正△BCE，连接CD、CE，求证△ABE≌△DBC。

分析：△ABE、△DBC有一个公共顶点，符合以上模型的一个要素，从而引导学生朝模型方向思考，寻找其余的“S”和“A”，显然由已知条件可得：

由于符合以上数学模型条件，从而快速找到解决问题的方法。

三、利用建模思想、拓宽思维空间，培养创新应用能力

任何数学试题特别是综合性题，都是将知识点和数学思想方法通过数量关系式结合起来，然后提出所需解决的问题。学习数学就是学习数学知识、数学思想、数学方法，目的是解决数学问题。利用数学建模思想能很好激发学生思维，明确思维方向、拓宽思维空间，从而提高学生的创新应用能力。

例3.在△ABC中(图2)，已知AB=AC，D、E分别在AB、AC，DE∥BC。将△ADE绕点A逆时针旋转(图3)，连接BD1、CE1。求证：△ABD1≌△ACE1。

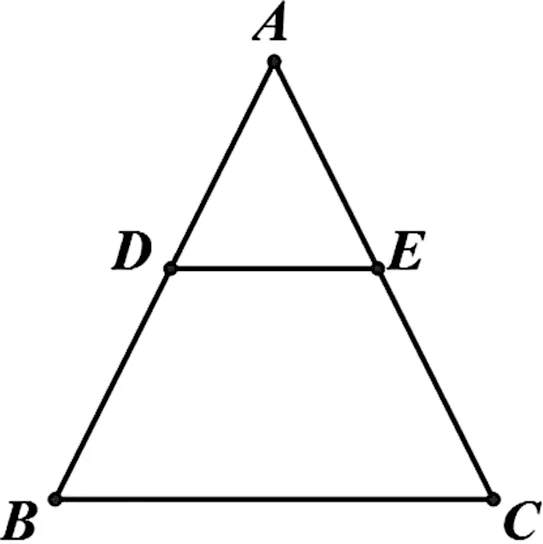
图2

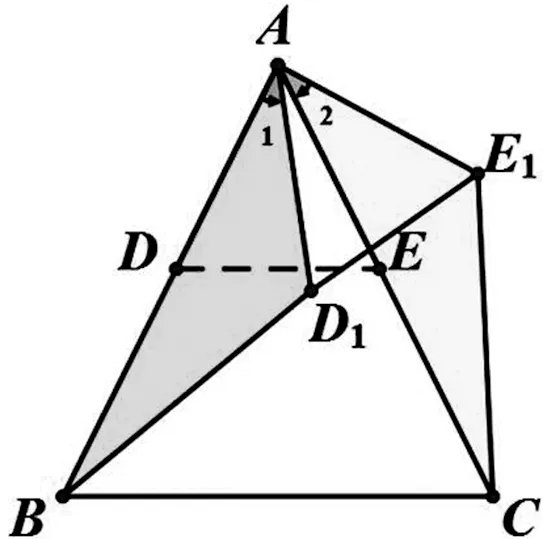
图3

分析：△ABD1与△ACE1，有一个公共顶点，能否用上面的模型来解决？引导学生思考：已知AB=AC，能否得到 ∠1=∠2 ？AD1=AE1?∵△ADE进行了旋转，∴旋转角：∠1=∠2，且AD=AD1，AE=AE1。要证：AD1=AE1，就要追溯AD=AE？

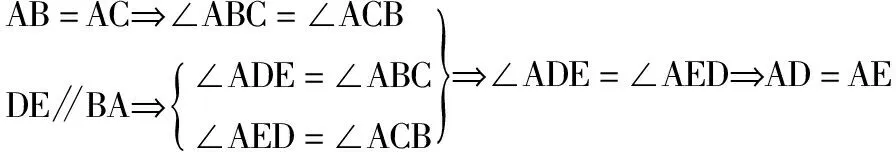
该题至此得证。

此时，教师继续设问，乘势引导学生思维向纵深奔跑，拓展学生思考空间。